Temperature Dependence of Germanium Arsenide Field-Effect Transistors Electrical Properties †
Abstract
:1. Introduction
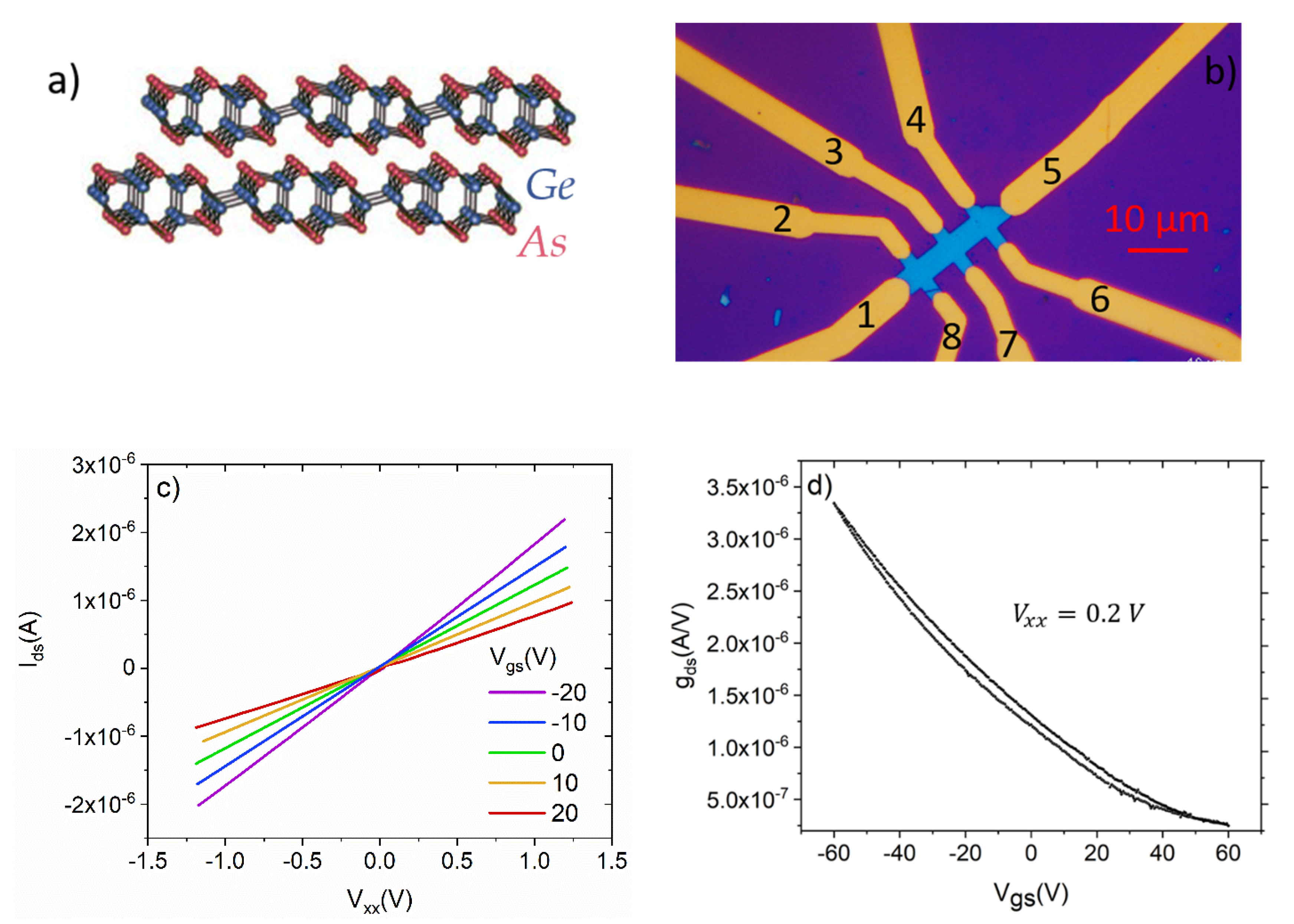
2. Results and Discussion
3. Conclusions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
References
- Wu, P.; Huang, M. Stability, bonding, and electronic properties of silicon and germanium arsenides: Stability, bonding, and electronic properties of Si and Ge arsenides. Phys. Status Solidi (b) 2016, 253, 862–867. [Google Scholar] [CrossRef]
- Jung, C.S.; Kim, D.; Cha, S.; Myung, Y.; Shojaei, F.; Abbas, H.G.; Lee, J.A.; Cha, E.H.; Park, J.; Kang, H.S. Two-dimensional GeAs with a visible range band gap. J. Mater. Chem. A 2018, 6, 9089–9098. [Google Scholar] [CrossRef]
- Cheng, A.-Q.; He, Z.; Zhao, J.; Zeng, H.; Chen, R.-S. Monolayered Silicon and Germanium Monopnictide Semiconductors: Excellent Stability, High Absorbance, and Strain Engineering of Electronic Properties. ACS Appl. Mater. Interfaces 2018, 10, 5133–5139. [Google Scholar] [CrossRef] [PubMed]
- Shojaei, F.; Kang, H.S. Electronic Structures and Li-Diffusion Properties of Group IV–V Layered Materials: Hexagonal Germanium Phosphide and Germanium Arsenide. J. Phys. Chem. C 2016, 120, 23842–23850. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Ma, Y.; Zhu, E.; Lee, S.; Lu, Z.; Zhao, Z.; Xu, C.; Lee, S.-J.; Wu, H.; et al. Few-Layer GeAs Field-Effect Transistors and Infrared Photodetectors. Adv. Mater. 2018, 30, 1705934. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, Y.; Wu, M.; Hu, C.; Shen, W.; Gong, Y.; Huang, L.; Jiang, C.; Zhang, Y.; Ajayan, P.M. Highly In-Plane Optical and Electrical Anisotropy of 2D Germanium Arsenide. Adv. Funct. Mater. 2018, 28, 1707379. [Google Scholar] [CrossRef]
- Blachnik, R.; Irle, E. Das System Gallium-Tellur. J. Less Common Met. 1985, 113, L1–L3. [Google Scholar] [CrossRef]
- Lee, K.; Kamali, S.; Ericsson, T.; Bellard, M.; Kovnir, K. GeAs: Highly Anisotropic van der Waals Thermoelectric Material. Chem. Mater. 2016, 28, 2776–2785. [Google Scholar] [CrossRef]
- Rau, J.W.; Kannewurf, C.R. Optical Absorption, Reflectivity, and Electrical Conductivity in GeAs and GeAs2. Phys. Rev. B 1971, 3, 2581–2587. [Google Scholar] [CrossRef]
- Zhou, L.; Guo, Y.; Zhao, J. GeAs and SiAs monolayers: Novel 2D semiconductors with suitable band structures. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 95, 149–153. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Cuniberti, G.; Zhuang, X. Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications. Coatings 2019, 9, 522. [Google Scholar] [CrossRef]
- Grillo, A.; Di Bartolomeo, A.; Urban, F.; Passacantando, M.; Caridad, J.M.; Sun, J.; Camilli, L. Observation of 2D Conduction in Ultrathin Germanium Arsenide Field-Effect Transistors. ACS Appl. Mater. Interfaces 2020, 12, 12998–13004. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A.; Genovese, L.; Giubileo, F.; Iemmo, L.; Luongo, G.; Foller, T.; Schleberger, M. Hysteresis in the transfer characteristics of MoS 2 transistors. 2D Mater. 2017, 5, 015014. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2007; ISBN 978-0-471-14323-9. [Google Scholar]
- Mott, N.F. Conduction in glasses containing transition metal ions. J. Non-Cryst. Solids 1968, 1, 1–17. [Google Scholar] [CrossRef]
- Barreteau, C.; Michon, B.; Besnard, C.; Giannini, E. High-pressure melt growth and transport properties of SiP, SiAs, GeP, and GeAs 2D layered semiconductors. J. Cryst. Growth 2016, 443, 75–80. [Google Scholar] [CrossRef]
- Ang, Y.S.; Yang, H.Y.; Ang, L.K. Universal Scaling Laws in Schottky Heterostructures Based on Two-Dimensional Materials. Phys. Rev. Lett. 2018, 121, 056802. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; He, Q.; Wu, H.; Cheng, H.-C.; Ding, M.; Shakir, I.; Gambin, V.; Huang, Y.; Duan, X. Vertical Charge Transport and Negative Transconductance in Multilayer Molybdenum Disulfides. Nano Lett. 2017, 17, 5495–5501. [Google Scholar] [CrossRef]
- Ji, H.; Ghimire, M.K.; Lee, G.; Yi, H.; Sakong, W.; Gul, H.Z.; Yun, Y.; Jiang, J.; Kim, J.; Joo, M.-K.; et al. Temperature-Dependent Opacity of the Gate Field Inside MoS2 Field-Effect Transistors. ACS Appl. Mater. Interfaces 2019, 11, 29022–29028. [Google Scholar] [CrossRef] [PubMed]
- Mead, D.G. Long wavelength study of semiconducting germanium arsenide, GeAs. Infrared Phys. 1982, 22, 209–213. [Google Scholar] [CrossRef]

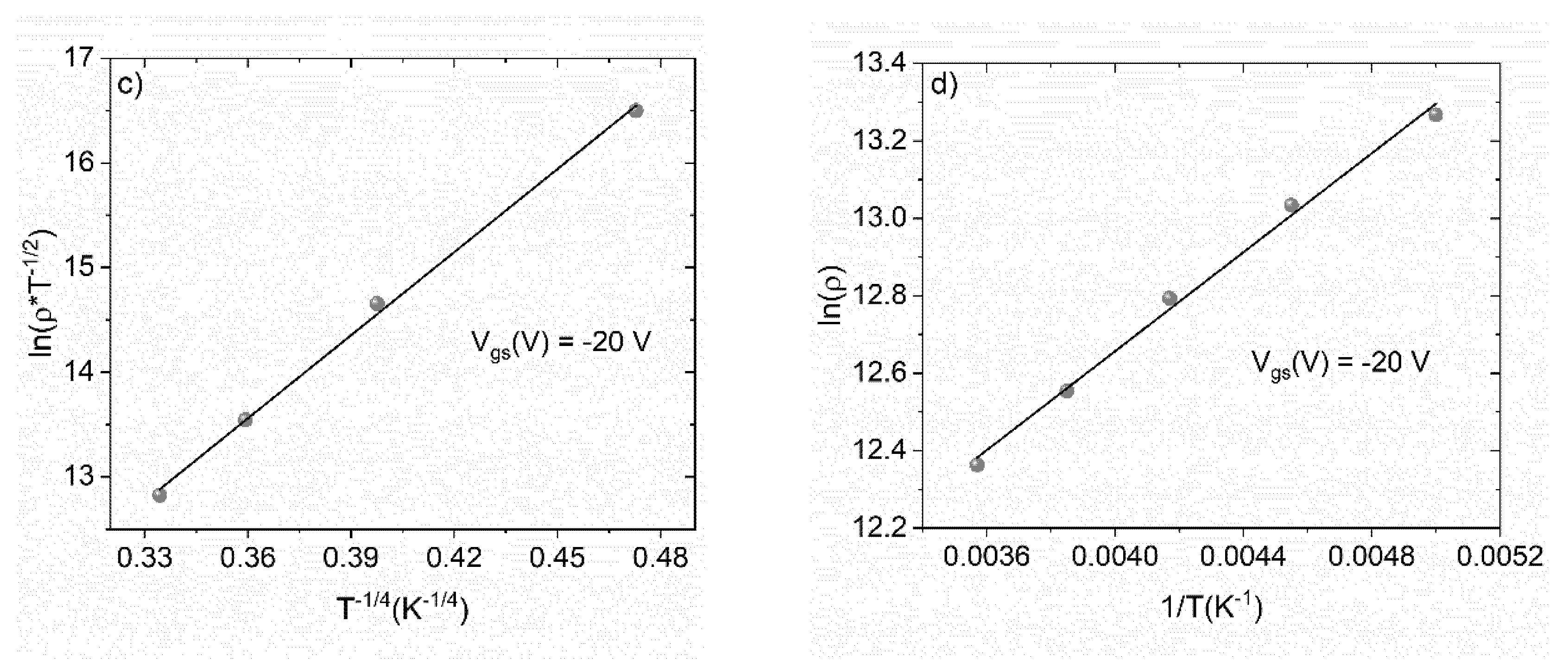

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grillo, A.; Faella, E.; Giubileo, F.; Pelella, A.; Urban, F.; Di Bartolomeo, A. Temperature Dependence of Germanium Arsenide Field-Effect Transistors Electrical Properties. Mater. Proc. 2021, 4, 26. https://doi.org/10.3390/IOCN2020-07810
Grillo A, Faella E, Giubileo F, Pelella A, Urban F, Di Bartolomeo A. Temperature Dependence of Germanium Arsenide Field-Effect Transistors Electrical Properties. Materials Proceedings. 2021; 4(1):26. https://doi.org/10.3390/IOCN2020-07810
Chicago/Turabian StyleGrillo, Alessandro, Enver Faella, Filippo Giubileo, Aniello Pelella, Francesca Urban, and Antonio Di Bartolomeo. 2021. "Temperature Dependence of Germanium Arsenide Field-Effect Transistors Electrical Properties" Materials Proceedings 4, no. 1: 26. https://doi.org/10.3390/IOCN2020-07810
APA StyleGrillo, A., Faella, E., Giubileo, F., Pelella, A., Urban, F., & Di Bartolomeo, A. (2021). Temperature Dependence of Germanium Arsenide Field-Effect Transistors Electrical Properties. Materials Proceedings, 4(1), 26. https://doi.org/10.3390/IOCN2020-07810









