Defect Reduction in Ferritic Stainless Steels through Modelling Plastic Deformation and Metallurgical Evolution ^†

Abstract

Steel products made of ferritic steel can show some defects, such as jagged edges, following the hot rolling process. Aiming to identify the origin of this type of defect in order to help their reduction, an in-depth study has been carried out considering the hot rolling conditions of flat bars made of EN 1.4512 steel. A wide number of references to austenitic stainless steel can be found in literature: almost all the semi-empirical models describing the microstructural evolution during hot deformation refer to austenitic stainless steel. In this work, a comprehensive model for recrystallization and grain growth of the ferritic stainless steel grade EN 1.4512 is proposed, enriching the literature and works regarding ferritic stainless steels. Thermomechanical and metallurgical models have been implemented. The microstructural evolution and the damage of the material were calculated through the coupling of metallurgical and damage models. In the thermomechanical simulations of the roughing passes, three granulometry levels (PFGS) and three heating furnace temperatures were considered. The ferritic grain evolution metallurgical model was obtained by introducing apposite equations. The results highlight that the defect could be produced by process conditions that spark abnormal heating and consequently uncontrolled growth of the grains. The work-hardened grains undergo elongation during hot deformation without recrystallizing. Those grains “squeeze” the surrounding recrystallized grains towards the edges. Thus, on the edges occurs a series of cracks that macroscopically manifest themselves as jagged edges.

1. Introduction

Ferritic stainless steels are characterized by a significantly lower cost than austenitic stainless steels; for this reason, they are increasingly in demand today. Ferritic steels are used in a wide range of applications that require resistance and ductility while maintaining high corrosion resistance requirements [1]. For this reason, the manufacturing of products made of ferritic stainless is in the steel industry’s interest. The industrial production feasibility of flat bars is not just limited to the use of micro-alloyed steels; as a matter of fact, ferritic steel bar manufacturing is a hot topic (e.g., EN 1.4512 steel grade).

Ferritic steel flat bars may exhibit defects such as the jagged edges, as shown in Figure 1. Jagged edges defects may appear during the hot rolling process of the ferritic bars.

The hot rolling process is characterized by high temperatures and a deformation field that can deeply modify the solidification structure of the steel. Furthermore, the roughing phase of the hot rolling process is a key part of the entire process due to the critical role of temperature, strain, strain rate, and also, the presence of waiting time between passes. It is known that the recrystallization processes (static, dynamic, meta dynamic) are influenced by the temperature, the amount of deformation, and the residence time under certain conditions [2,3].

The evolution of the ferritic microstructure is the key element to understand the nature of metallurgical defects. Anyway, regarding the microstructural evolution of austenitic stainless steel, a large number of models have been proposed by various authors to evaluate the evolution of austenite grains in a wide range of working conditions [4,5]. On the other hand, is not easy to find homogeneous literature on the evolution of the ferritic microstructure during hot deformation processes. Some authors have reported in the literature the deformation behavior of ferrite of IF (free interstitial) steels [6] and low carbon steels [7] subjected to plastic deformation. The aim of this work is, taking into account the studies carried out by previous authors, to propose a complete model for static and dynamic recrystallization.

Based on the above considerations, a mathematical model has been developed to take into account both static and meta-dynamic recrystallization. The metallurgical model has been tuned by considering the link between the rheological behavior of the material and the microstructural evolution of the steel during hot rolling.

The work presented in this paper aims to analyze and put in evidence the cause laying below the origin of the jagged edges defect, based on such model adoption. An in-depth study on the rolling conditions of EN 1.4512 is reported in the following.

2. Material and Methods

This paper aims to study the jagged defect on the edges of hot rolled EN 1.4512. Therefore, a detailed analysis was carried out on selected samples edge by scanning electron microscope (SEM) using backscattered and secondary electrons (see Figure 2). The image in Figure 2b shows abnormal and non-recrystallized grains inside the matrix, that squeezed out of the edge of the bar. These grains represent a possible cause of the jagged edge macroscopically observed.

The as-cast microstructure of the bar shows a central area, of medium thickness, with an average grain size of about 5000 μm. Towards the edges, the grain size decreases continuously reaching about 150 μm. This information was mathematically represented using a mathematical function describing the prior ferritic grain size (PFGS, Figure 3). In order to understand the influence of the initial grain size distribution on the microstructure evolution during the hot rolling process, simulations with the following PFGS were carried out:

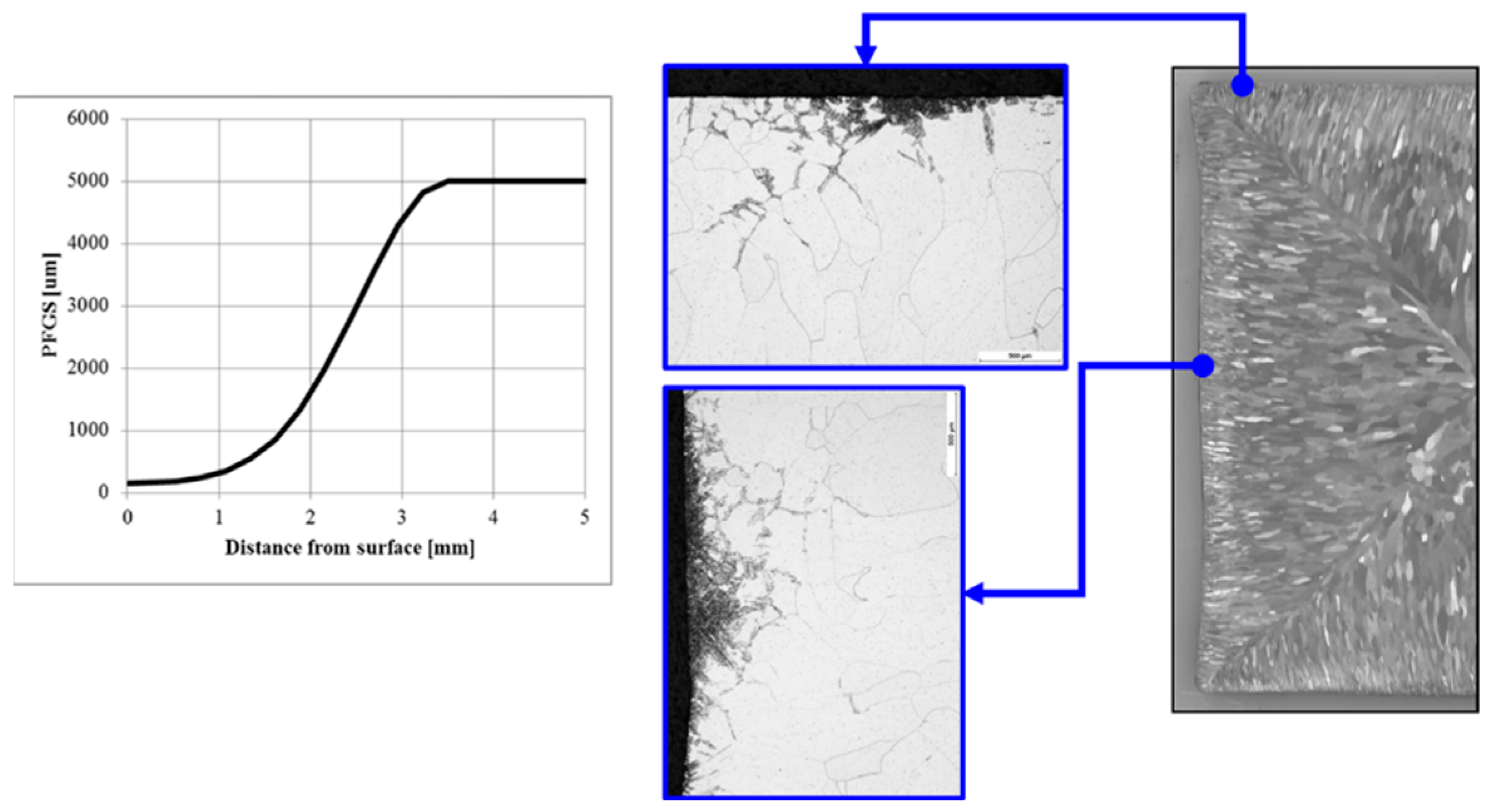
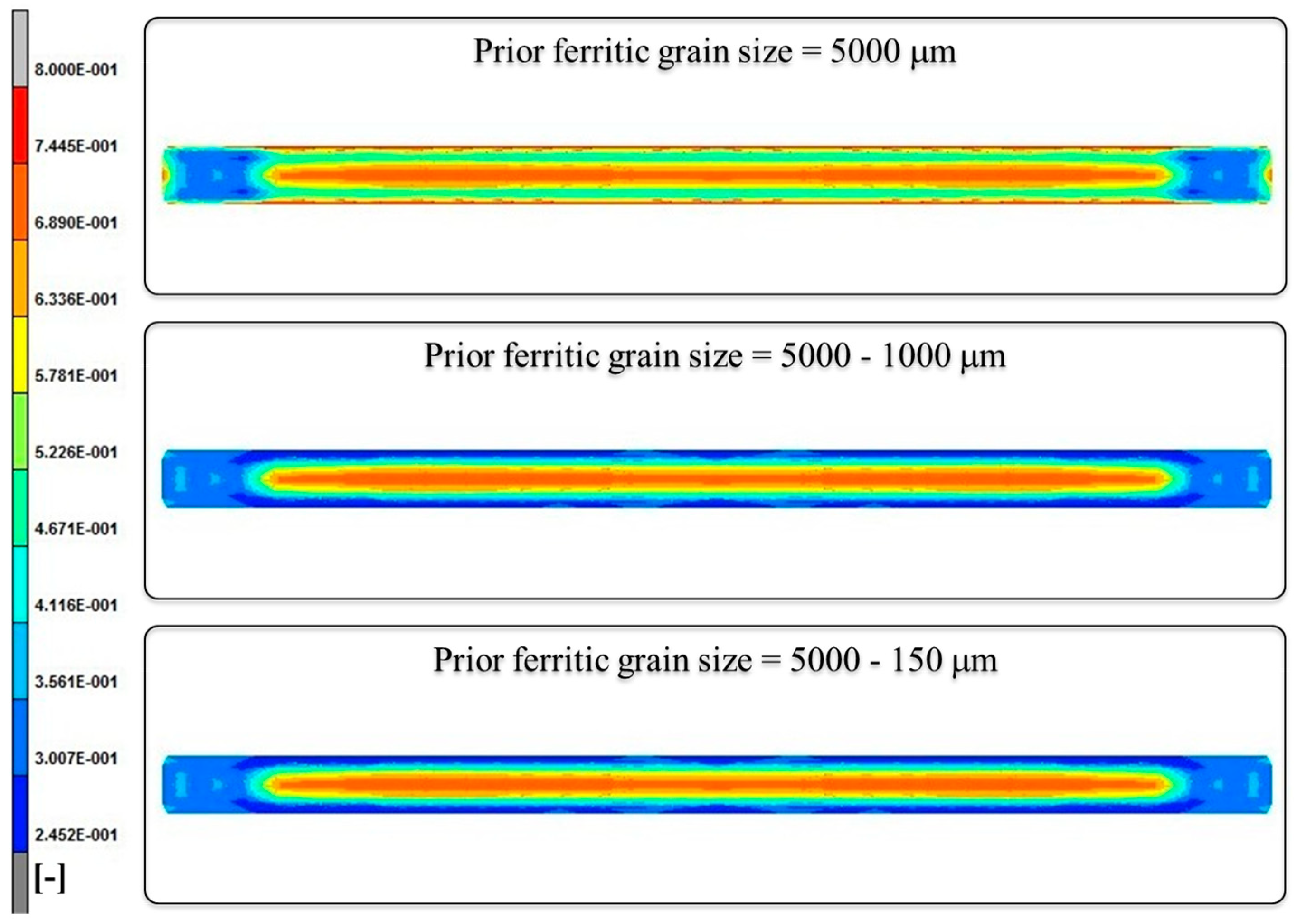
• A reference condition with grain size ranging from 5000 μm in the centre to 150 μm on the surface.
• A uniform grain size of 5000 μm average size.
• A grain size of 5000 µm in the center up to 1000 μm on the surface.

The material mechanical behavior during the plastic deformation process was implemented through the approach proposed by Spittel [8]. In this approach, the mechanical behavior is defined as a function of strain, strain rate and temperature through appropriate factors (Equation (1)). The model, represented by Equation (1), can be used in the case of the applied deformations lower than the peak deformation. The peak strain ε_p is expressed using Equation (2), taking into account the Zener—Hollomon parameter (evaluated according to Equation (3). Above the peak strain the material damage mechanism needs to be accounted: the damage model, based on a modified Lemaitre equation in Equation (4) [9] was implemented in the finite element model by means of an appropriate user subroutine.

$${\sigma }_{F }=A\ast {\left(\epsilon +{\epsilon }_0\right)}^{m_2}\ast {\left(\dot{\epsilon }+\dot{{\epsilon }_0}\right)}^{m_{8}T}\ast e^{m_{1}T}$$

(1)

$${\mathsf{\epsilon }}_{\mathrm{p}}= \mathsf{\alpha }{\left(\mathrm{Z}\right)}^{\mathsf{\beta }}$$

(2)

$${\mathsf{\epsilon }}_{\mathrm{p}}= \mathsf{\alpha }{\left(\mathrm{Z}\right)}^{\mathsf{\beta }}$$

(3)

$$\dot{D}={\left(-\frac{h_{c}y}{S_0}\right)}^{s_1-s_2{D}_{in}}{\overline{\dot{\epsilon }}}_p$$

(4)

Tensile tests were performed on EN 1.4512 steel in the temperature range 750–1200 °C, at strain rates of 0.1 s⁻¹ and 5.0 s⁻¹. The tests were simulated through finite element analysis in order to model through Equations (1)–(4) the stress–strain curve.

Once the material model was fine-tuned using parameters in Equations (1) and (4), a thermomechanical hot rolling 3D model was implemented. The finite element model of the industrial hot rolling process was tuned in terms of heat transfer coefficient (HTC). The waiting time between passes was evaluated by analyzing the signals acquired in terms of rolling force during hot rolling.

2.1. Static Recrystalization and Grain Growth Models

In this paper, the following mechanisms that occur during the hot rolling process were considered: static recrystallization (SRX) (which occurs during the waiting time between roughing passes of the hot rolling process), metadynamic recrystallization (MDRX), grain growth (GG) after recrystallization. SRX was modelled by an Avrami-type equation that expresses the recrystallized fraction X_rex as a function of time in isothermal conditions (Equation (5)). In Equation (5), t_0.5 is the time in which 50% of SRX occurred; t_0.5 (Equation (6)) depends on initial grain size, the temperature, the deformation, and the deformation rate through suitable coefficients. The SRX mechanism is activated when the steel undergoes conditions of low strain rate levels. In this case, the size of the recrystallized grain indicated with d_srx (Equation (7)) can be expressed using appropriate parameters. The activation energy Q was determined starting from the literature data in [10]. The growth of the grain was modelled using Equation (8).

$$X_{rex}=1-exp\left[-0.693{\left(\frac{t}{t_{0.5}}\right)}^n\right]$$

(5)

$$t_{0.5}=C{\epsilon }^p{\dot{\epsilon }}^q{d}^{s}exp\left(\frac{Q_{app}}{RT}\right)$$

(6)

$$d_{SRX }=c_{1 }+c_{2 }{d}_{\alpha }{}^{c_3}{\epsilon }^{c_4}{\left(\dot{\epsilon }exp\left(\frac{Q}{RT}\right)\right)}^{c_5}$$

(7)

$$d_{gg}={\left(d_{\alpha }{}^{c_1}+c_{2 }exp\left(\frac{Q}{RT}\right)t_{gg}\right)}^{c^{-3}}$$

(8)

2.2. Meta-Dynamic Recrystalization and Grain Growth Models

Experimental data found in the literature on stainless steels characterized by high chromium content indicate that MDRX is the dominant process when high levels of deformation and high temperatures are considered [11]. MDRX is activated when the imposed strain exceeds a critical level ε_C, a parameter which is proportional to the peak strain, estimated though a collection of literature data [11,12]. The recrystallized fraction after recrystallization was calculated using the same Equation (1) illustrated in static recrystallization. Instead, the size of the ferrite grains after MDRX was calculated according to Equation (9).

$${\mathrm{d}}_{\mathrm{MDRX}}={ \mathrm{c}}_1 \mathsf{\epsilon }\exp {\left(\frac{\mathrm{Q}}{\mathrm{RT}}\right)}^{{\mathrm{c}}_2}$$

(9)

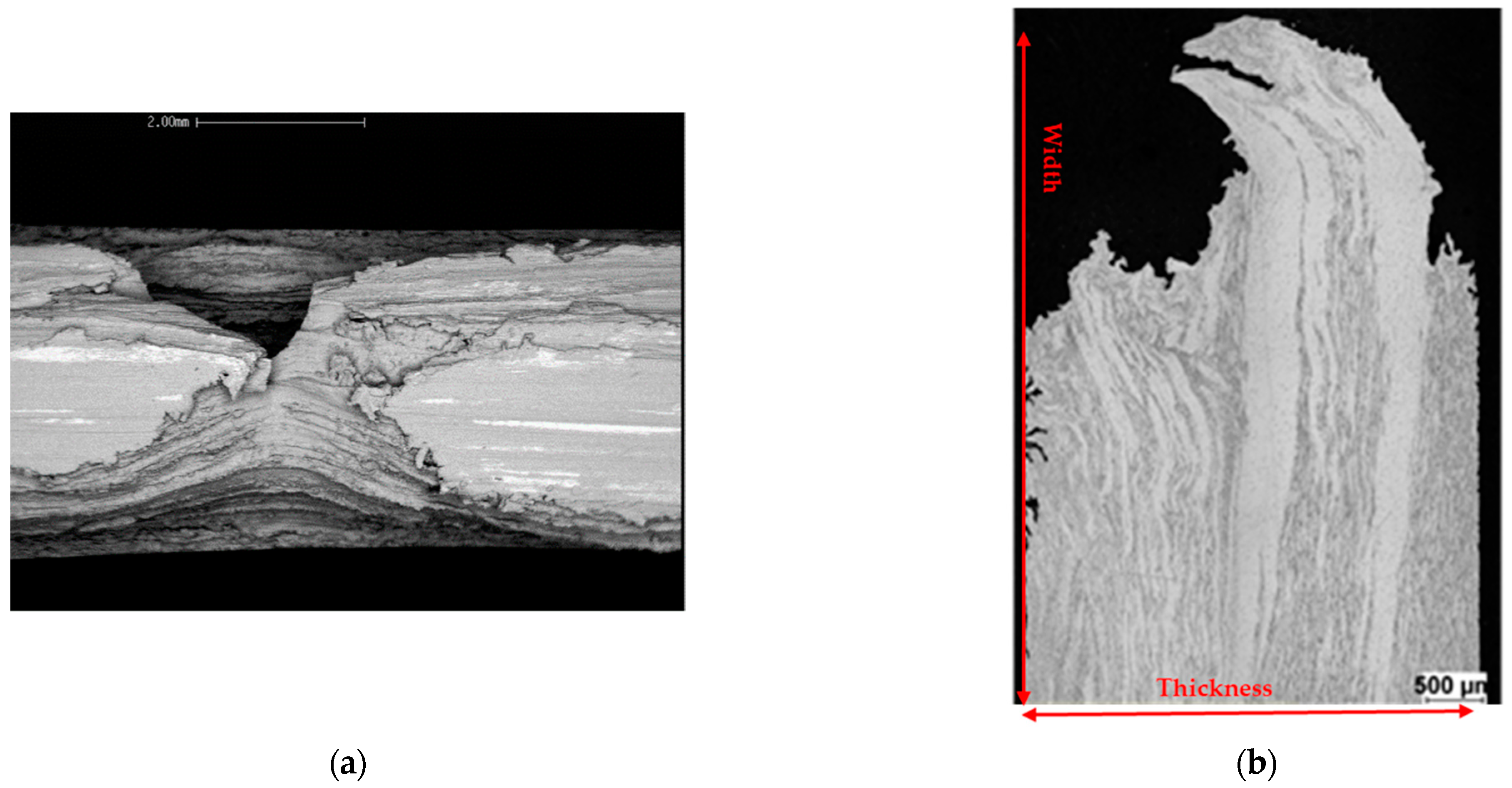
3. Results and Discussion

The output of the thermo-mechanical FE simulations and the microstructural model were coupled in order to simulate the evolution of the microstructure during the roughing step of the hot rolling process. The damage model, based on the modified Lemaitre equation, was implemented in the finite element model by using a specific subroutine.

In order to visualize the effect of the heating temperature, the prior ferritic grain size (PFGS) and all the simulated parameters, 2D maps were built on the cross section of the bar subjected to the rolling process as shown in Figure 4 and Figure 5 [13]. It has been observed that the prior ferritic grain is a source of considerable differences in the microstructure: the as-cast structure of the bar can undergo uncontrolled growth due to inadequate heating conditions causing the defect of the jagged edges.

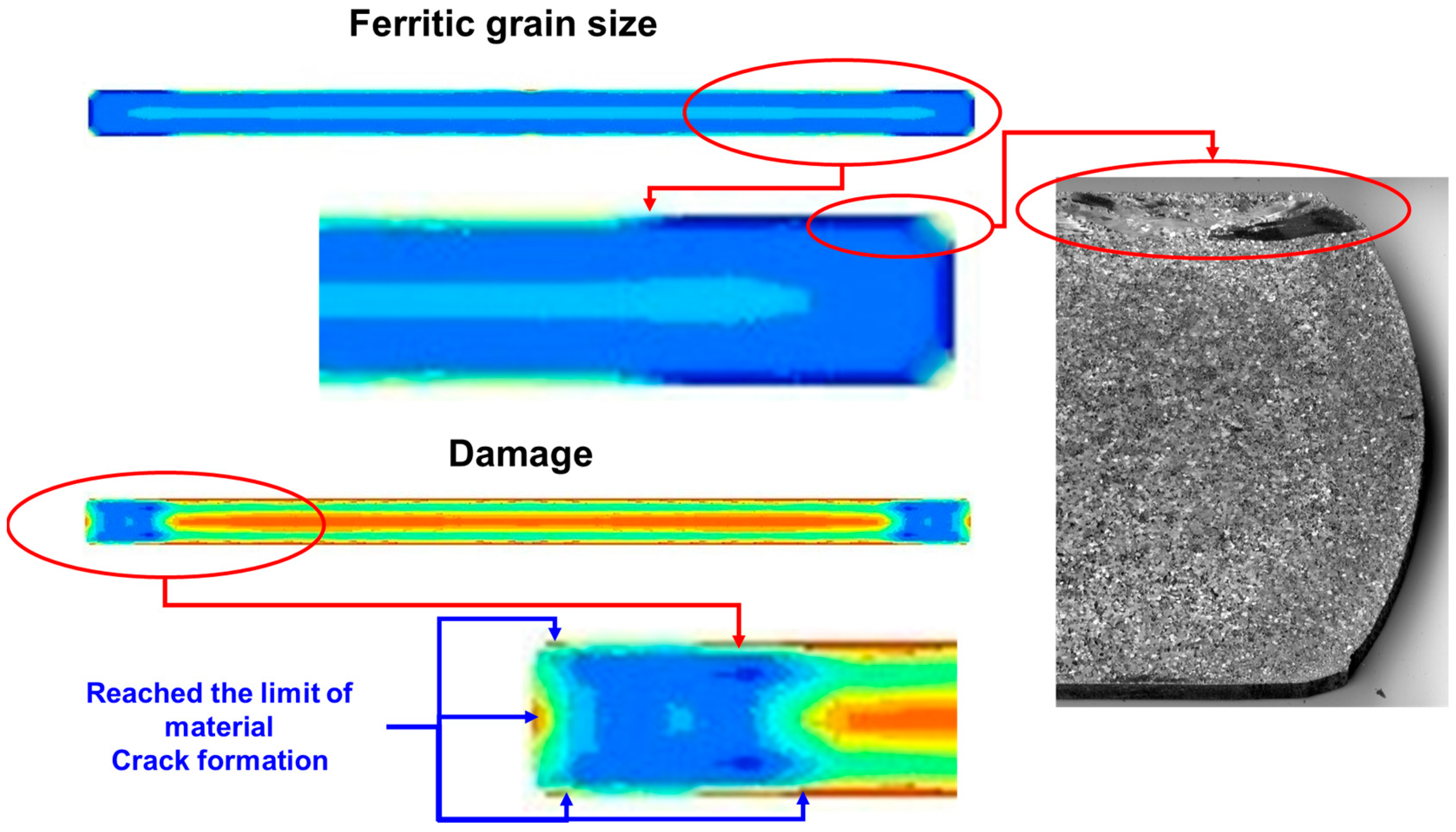
4. Conclusions

Results showed that the jagged defect could be caused by uncontrolled reheating of the bars during the hot rolling process. FE analysis showed that a smaller initial grain size doesn’t produce the defect. In this case, the bar is characterized by smaller grains near the surface and coarser grains at the core. A uniform and coarse ferrite grain size of 5000 mm, on the contrary, could develop the defect when the bar is subjected to improper heating or cooling phase during the process. When it comes to the hot rolling process, the work-hardened grains undergo severe elongation without being able to recrystallize. Consequently, these grains “squeeze” the surrounding matrix, characterized by new recrystallized grains, towards the edges of the bar where fractures occur, appearing at a macroscopical level as jagged edges.