Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses †
Abstract
:1. Introduction
2. Parametric ALT for a Mechanical System
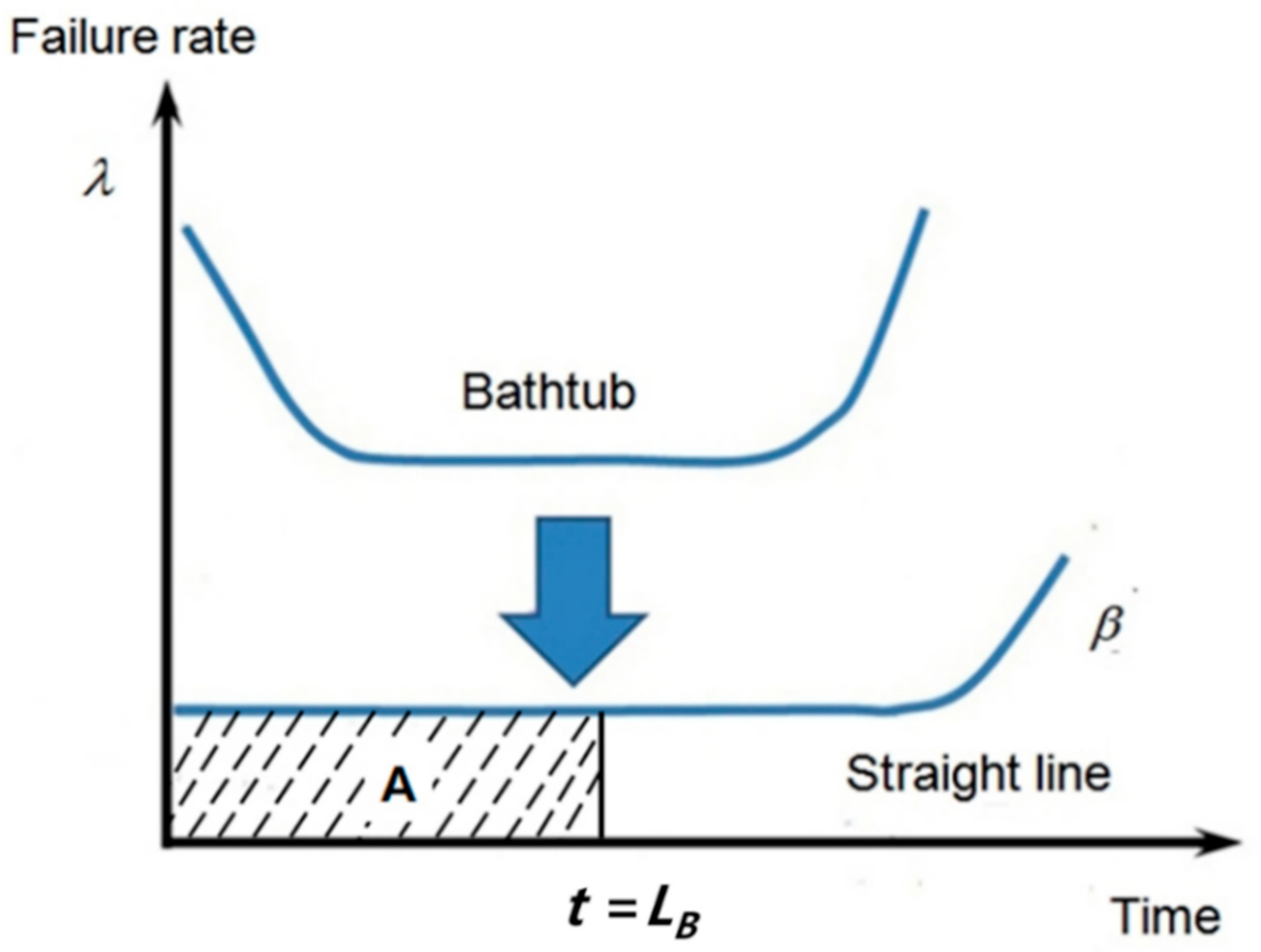
2.1. Definition of BX Lifetime
2.2. Setting A Whole Parametric ALT Plan
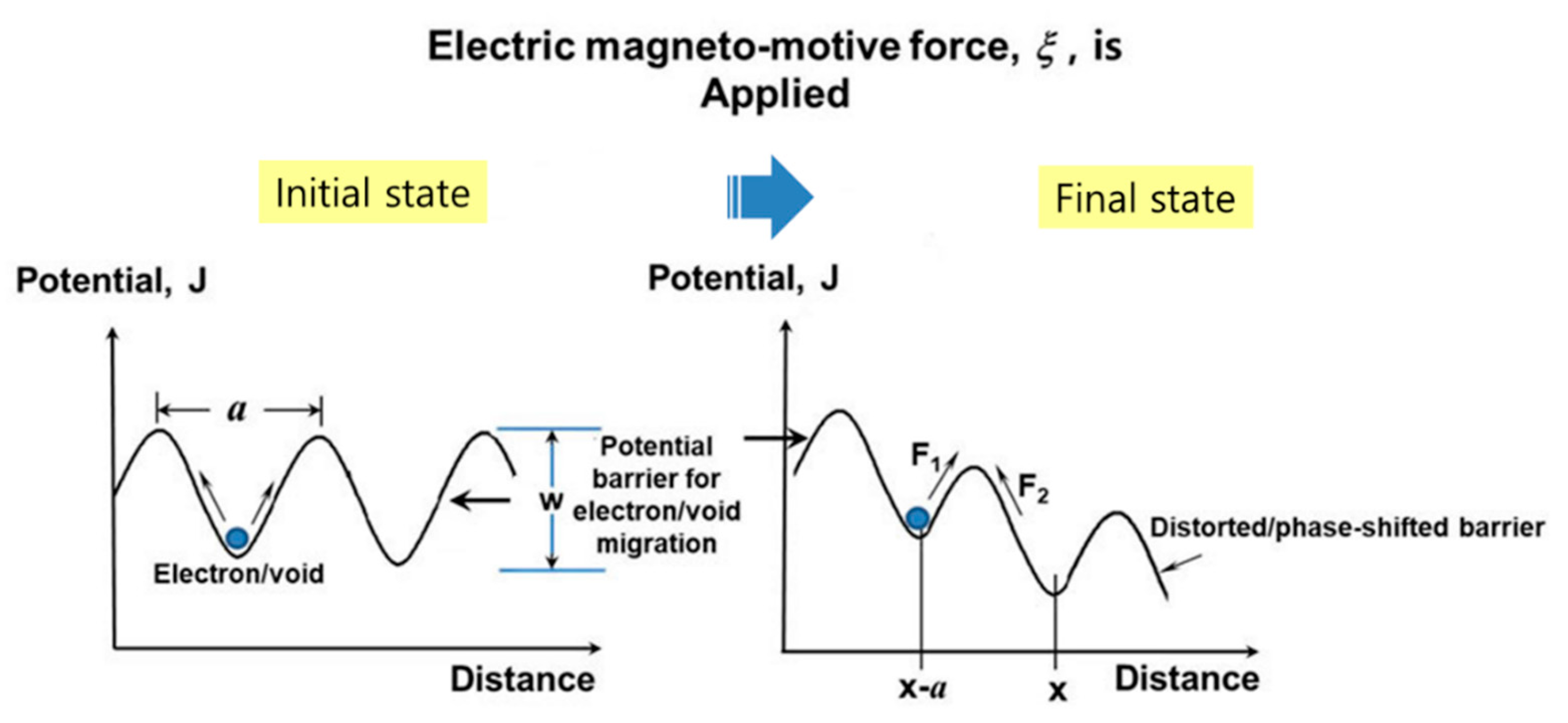
2.3. Failure Mechanics and Parametric ALT for Design
- in Equation (8) has a little linear effect at first;
- in Equation (8) has what is regarded as a medium effect; and
- in Equation (8) is big in the end.
2.4. Parametric ALT for Mechanical Systems
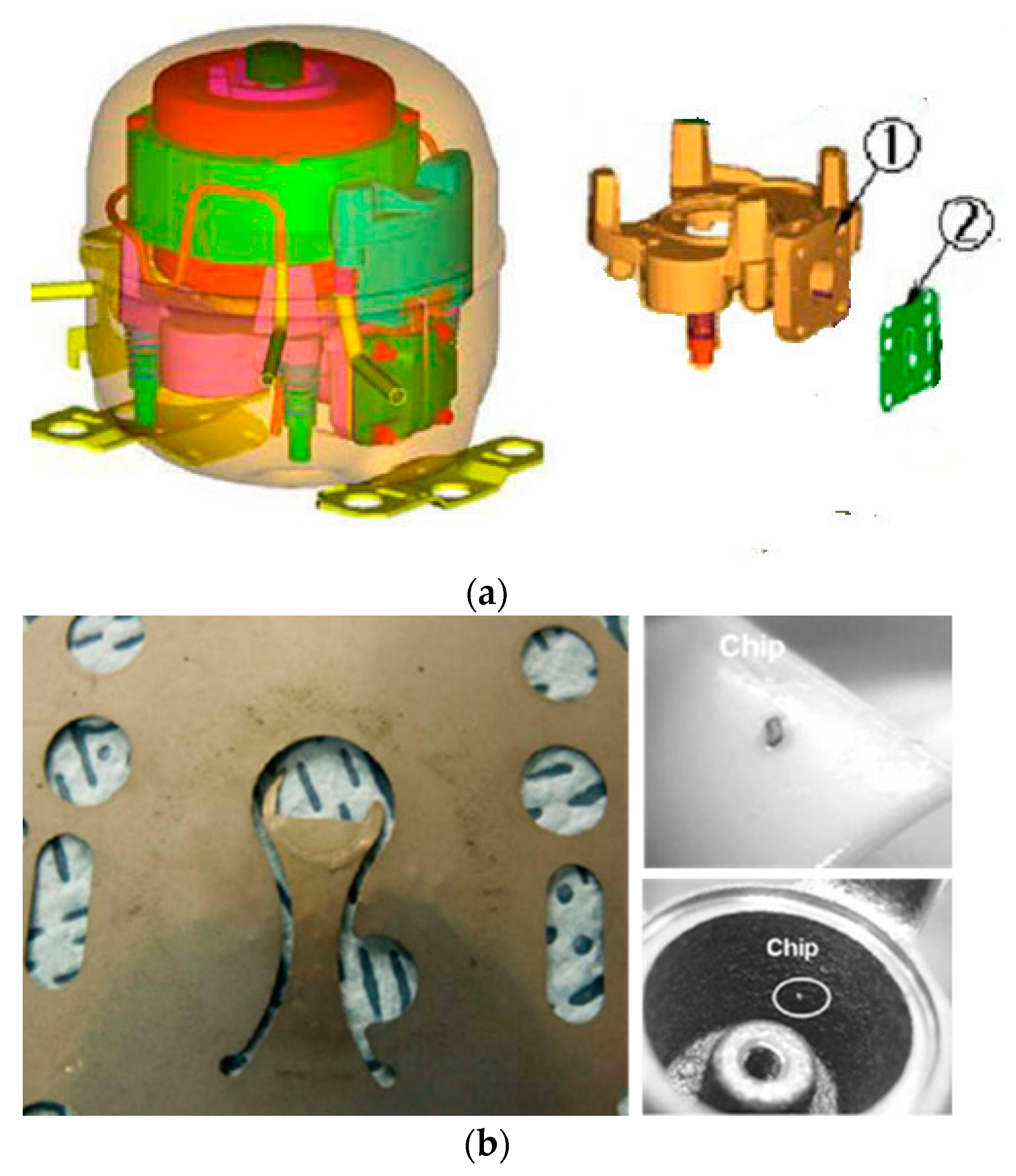
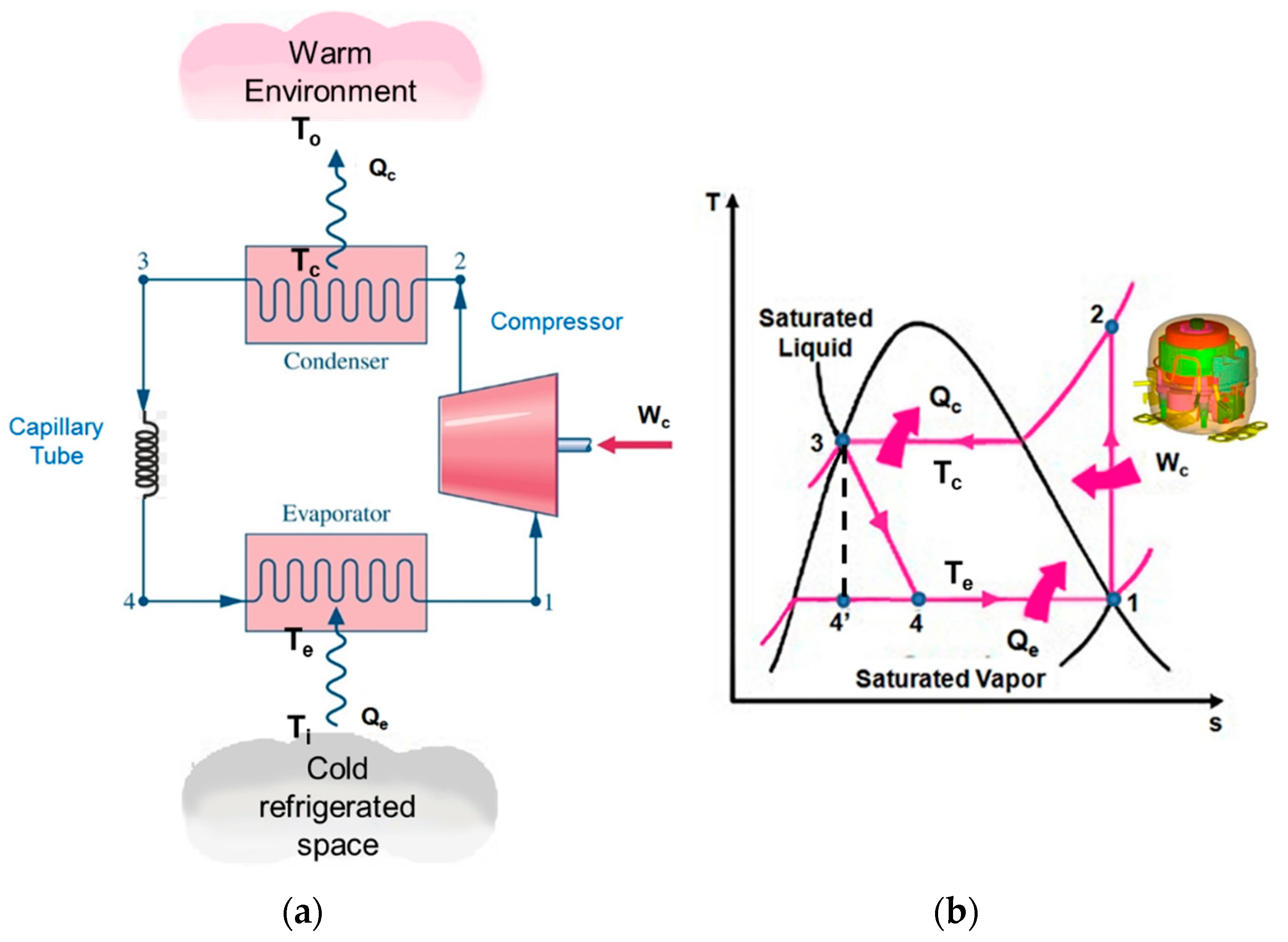
2.5. Case Study—Reliability Design of a Newly Designed Compressor in Domestic Refrigerator
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Cross-sectional area of the capillary tube, cm2 |
| BX | time that is an accumulated failure rate of X%, durability index |
| Ea | activation energy, eV |
| e | effort |
| f | flow |
| F | impact force, kN |
| F(t) | unreliability |
| h | testing cycles (or cycles) |
| h* | nondimensional testing cycles, |
| J | junction equation |
| K | Boltzmann’s constant, 8.62 × 10−5 eV/deg |
| ΔL | Capillary tube length in the two-phase |
| LB | target BX life and x = 0.01X, on the condition that x ≤ 0.2 |
| N | number of test samples |
| ΔP | Pressure difference between the condenser and evaporator, MPa |
| PD | Volume flow rate in compressor, m3/s |
| Pc | Pressure in the condenser, MPa |
| Pe | Pressure in the evaporator, MPa |
| Psuc | Pressure at compressor suction, MPa |
| Pdis | Pressure at compressor discharge, MPa |
| Q | amount of energy absorbed or released during the reaction. For the semiconductor total number of dopants per unit area |
| Qc | Heat transfer by temperature difference in the condenser, kW |
| Qe | Heat transfer by temperature difference in the evaporator, kW |
| R | ratio for minmum stress to maximum stress in stress cycle, σmin/σmax |
| R | failed numbers |
| Rc | Thermal resistance in the condenser, K/kW |
| Re | Thermal resistance in the evaporator, K/kW |
| S | stress |
| T | torque around the hinge kit system, kN m |
| T | temperature, K |
| Tc | Absolute temperature in the Condenser, K |
| Te | Absolute temperature in the Evaporator, K |
| ti | test time for each sample |
| TF | time to failure |
| X | accumulated failure rate, % |
| x | x = 0.01X, on condition that x ≤ 0.2. |
| Wc | Compressor power, kW |
| Greek symbols | |
| ξ | electrical field applied |
| η | characteristic life |
| λ | cumulative damage exponent in Palmgren–Miner’s rule |
| χ2 | chi-square distribution |
| α | confidence level |
| νsuc | Specific volume of refrigerant at compressor suction, m3/kg |
| ρ | Refrigerant density, kg/m3 |
| ηv | Volumetric efficiency |
| ω | Angular velocity, rad/s |
| Superscripts | |
| β | shape parameter in Weibull distribution |
| n | stress dependence, |
| Subscripts | |
| 0 | normal stress conditions |
| 1 | accelerated stress conditions |
References
- Woo, S.; O’Neal, D.; Woldemichael, D.E.; Atnaw, S.M.; Tulu, M.M. Improving the Fatigue of Newly Designed Mechanical System Subjected to Repeated Impact Loading. Metals 2021, 11, 139. [Google Scholar] [CrossRef]
- Deming, W.E. Elementary Principles of the Statistical Control of Quality; Japan JUSE: Tokyo, Japan, 1950. [Google Scholar]
- Magaziner, I.C.; Patinkin, M. Cold competition: GE wages the refrigerator war. Harv. Bus. Rev. 1989, 89, 114–124. [Google Scholar]
- Taguchi, G. Off-line and on-line quality control systems. In Proceedings of the International Conference on Quality Control, Tokyo, Japan, October 1978. [Google Scholar]
- Chowdhury, S.; Taguchi, S. Robust Optimization: World’s Best Practices for Developing Winning Vehicles, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Allen, P. Design of Experiments for 21st Century Engineers, 1st ed.; Lulu Press: Morrisville, NC, USA, 2020. [Google Scholar]
- Duga, J.J.; Fisher, W.H.; Buxaum, R.W.; Rosenfield, A.R.; Buhr, A.R.; Honton, E.J.; McMillan, S.C. The Economic Effects of Fracture in the United States; Final Report; A Report to NBS Special Publication 647-2; Battelle Laboratories: Columbus, OH, USA, 30 September 1982. [Google Scholar]
- Fatigue. In Elements of Metallurgy and Engineering Alloys; Campbell, F.C. (Ed.) ASM International: Materials Park, OH, USA, 2008. [Google Scholar]
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Elsayed, E.A. Reliability Engineering; Addison Wesley Longman: Reading, MA, USA, 1996. [Google Scholar]
- Hahn, G.J.; Meeker, W.Q. How to Plan an Accelerated Life Test (E-Book); ASQ Quality Press: Milwaukee, WI, USA, 2004. [Google Scholar]
- McPherson, J. Accelerated testing. In Electronic Materials Handbook Volume 1: Packaging; ASM International Publishing: Materials Park, OH, USA, 1989; pp. 887–894. [Google Scholar]
- McPherson, J. Reliability Physics and Engineering: Time-to-Failure Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar]
- Irwin, G. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics—Fundamentals and Applications, 3rd ed.; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- ASTM E606/E606M. Standard Test Method for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- ASTM E399. Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- ASTM E647. Standard Test Method for Measurement of Fatigue Crack Growth Rates; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ASTM E739-10. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Braco, R.; Prates, P.; Costa, J.D.M.; Berto, F. New methodology of fatigue life evaluation for multiaxially loaded notched components based on two uniaxial strain-controlled tests. Int. J. Fatigue 2018, 111, 308–320. [Google Scholar] [CrossRef]
- Goodno, B.J.; Gere, J.M. Mechanics of Materials, 9th ed.; Thomson Brooks Cole Learning: Boston, MA, USA, 2020. [Google Scholar]
- Hertzberg, R.W.; Vinci, R.P.; Hertzberg, J.L. Deformation and Fracture Mechanics of Engineering Materials, 6th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Reddy, J.N. An Introduction to the Finite Element Method, 4th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- IEEE Standard Glossary of Software Engineering Terminology. IEEE STD 610.12-1990. Standards Coordinating Committee of the Computer Society of IEEE. (Reaffirmed September 2002). Available online: https://ieeexplore.ieee.org/document/159342 (accessed on 31 December 1990).
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley and Son: Hoboken, NJ, USA, 2011; p. 683. [Google Scholar]
- Grove, A. Physics and Technology of Semiconductor Device, 1st ed.; Wiley International Edition: New York, NY, USA, 1967; p. 37. [Google Scholar]
- Minges, M.L. Electronic Materials Handbook; ASM International: Cleveland, OH, USA, 1989; Volume 1, p. 888. [Google Scholar]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems, 6th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Abernethy, R.B. The New Weibull Handbook; Reliability Analysis Center: North Palm Beach, FL, USA, 2000; pp. 2–6. [Google Scholar]



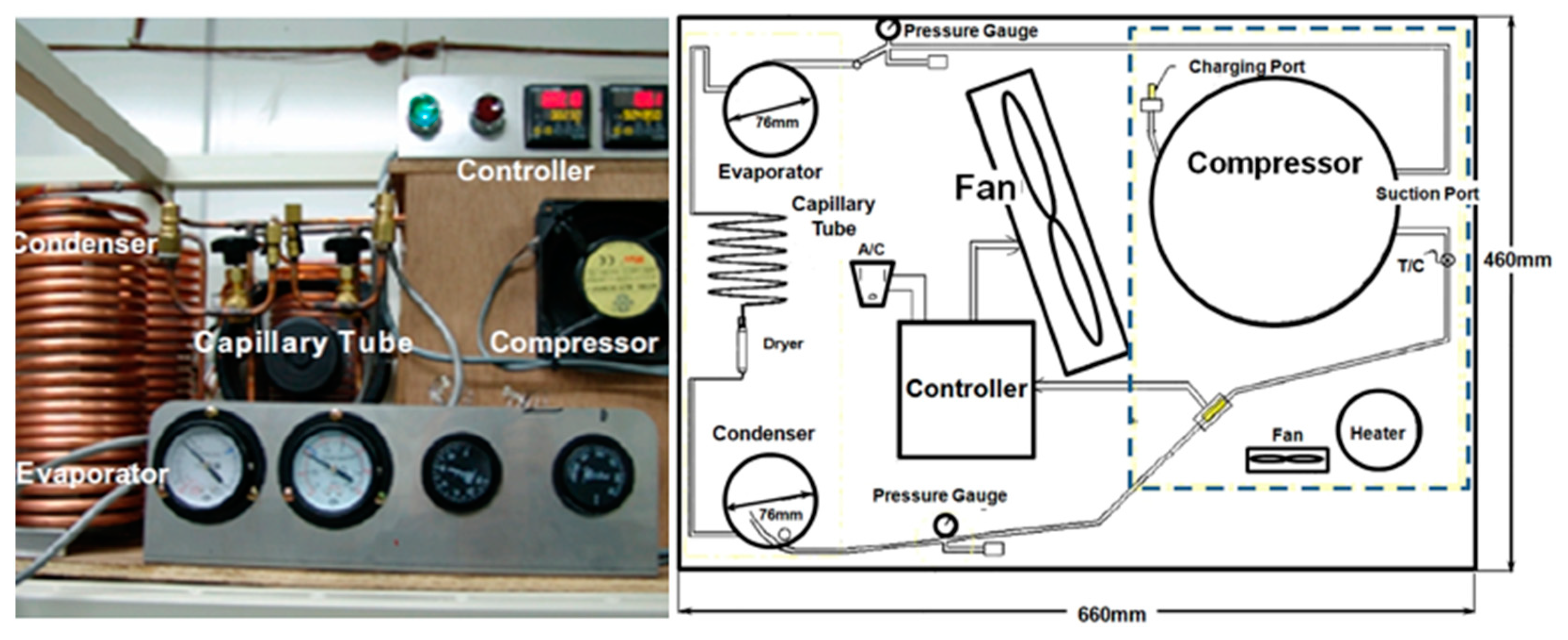

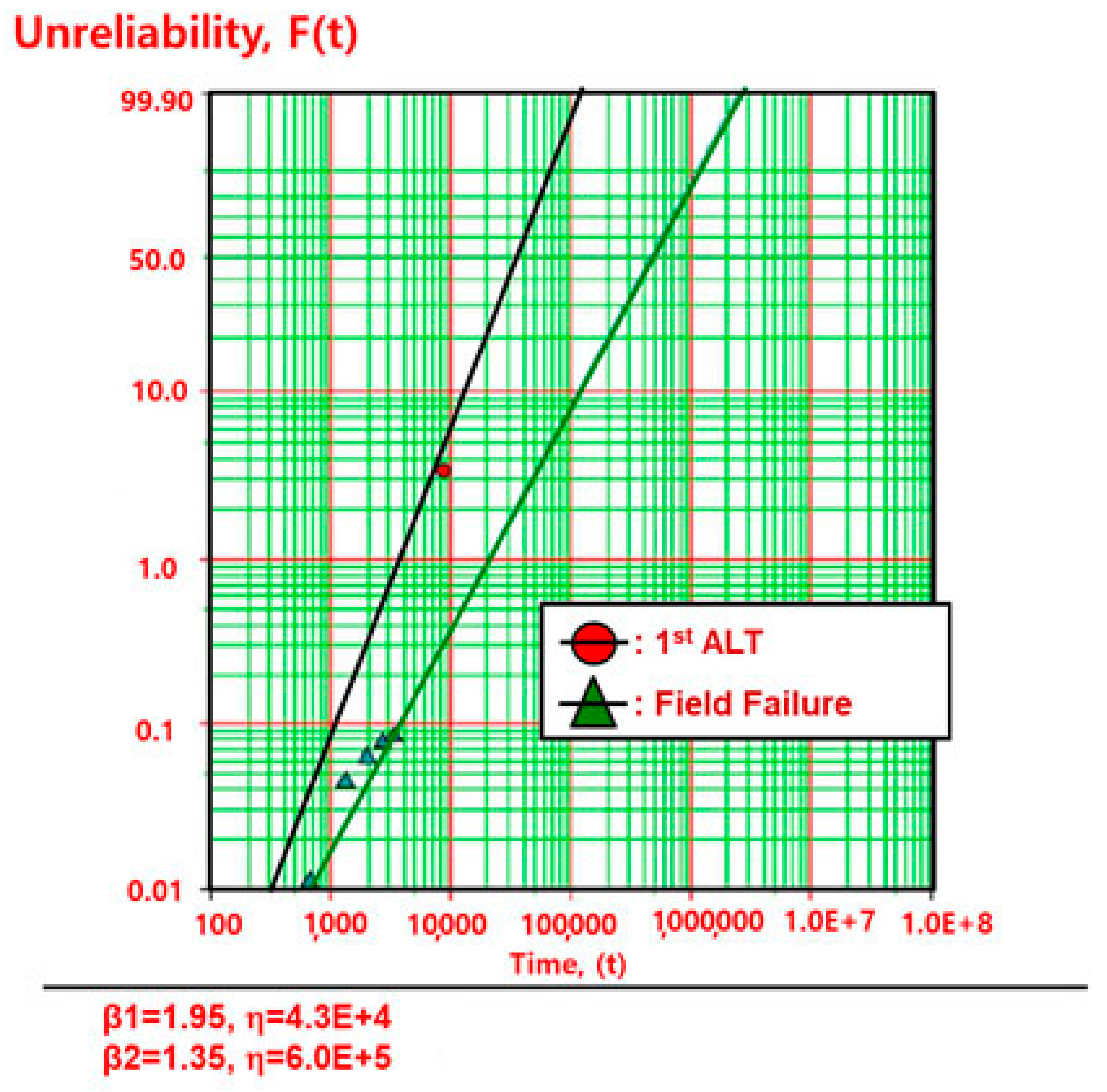
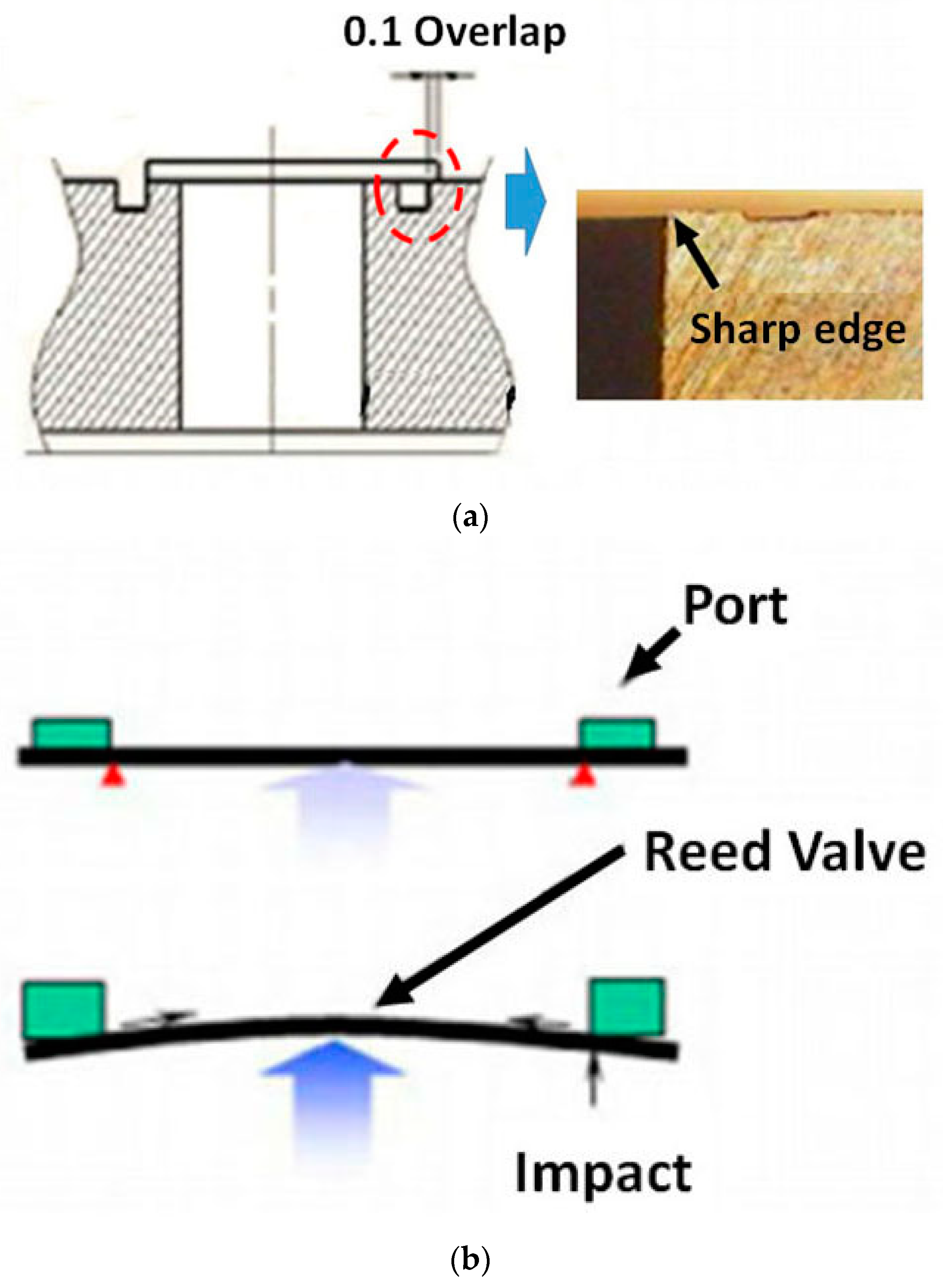
| Modules | Market Data | Anticipated Reliability | Objective Reliability | |||||
|---|---|---|---|---|---|---|---|---|
| Failure Rate Per Year, %/Year | BX Life, Year | Failure Rate Per Year, %/Year | BX Life, Year | Failure Rate Per Year, %/Year | BX Life, Year | |||
| A | 0.35 | 2.9 | Similar | ×1 | 0.35 | 2.9 | 0.10 | 10(BX = 1.0) |
| B | 0.24 | 4.2 | New | ×5 | 1.20 | 0.83 | 0.10 | 10(BX = 1.0) |
| C | 0.30 | 3.3 | Similar | ×1 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| D | 0.31 | 3.2 | Modified | ×2 | 0.62 | 1.61 | 0.10 | 10(BX = 1.0) |
| E | 0.15 | 6.7 | Modified | ×2 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| Others | 0.50 | 10.0 | Similar | ×1 | 0.50 | 10.0 | 0.50 | 10(BX = 5.0) |
| Product | 1.9 | 2.9 | - | - | 3.27 | 0.83 | 1.00 | 10(BX = 10) |
| System | Effort, e(t) | Flow, f(t) |
|---|---|---|
| Translation system | Force, F(t) | Velocity, V(t) |
| Rotation system | Torque, τ(t) | Angular velocity, ω(t) |
| Pump, Compressor | Pressure difference, ΔP(t) | Volume flow rate, Q(t) |
| Electric system | Voltage, V(t) | Current, i(t) |
| Magnetic | Magneto-motive force, em | Magnetic flux, φ |
| System States | Worst Case | ALT | AF | |
|---|---|---|---|---|
| Pressure (MPa) | High-side | 1.27 | 2.94 | 5.36 ① |
| Low-side | 0 | 0 | ||
| ΔP | 1.27 | 2.94 | ||
| Temperature (°C) Total AF (=(① × ②)) | Dome | 90 | 120 | 1.37 ② 7.32 |
| Parametric ALT | 1st ALT | 2nd ALT | 3rd ALT |
|---|---|---|---|
| Initial Design | Second Design | Last Design | |
| In 49,000 cycles, there are no problems in the compressor | 10,500 cycles: 1/100 locking | 17,000 Cycles: 3/100 locking | 49,000 cycles: 100/100 OK |
| Structure |  |  | - |
| Action plans | C1: Trepan size: 0.73 mm→1.25 mm C2: Attaching ball peening and brush process C3: SANDVIK 20C: 0.178 t→0.203 t C4: Expanding tumbling: 4 h→14 h | C5: FCD500 + No Heat Treatment → FCD500 + Heat Treatment on the crank shaft | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, S.; O’Neal, D.L.; Atnaw, S.M.; Tulu, M.M. Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses. Mater. Proc. 2021, 3, 14. https://doi.org/10.3390/IEC2M-09257
Woo S, O’Neal DL, Atnaw SM, Tulu MM. Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses. Materials Proceedings. 2021; 3(1):14. https://doi.org/10.3390/IEC2M-09257
Chicago/Turabian StyleWoo, Seongwoo, Dennis L. O’Neal, Samson Mekbib Atnaw, and Muluneh Mekonnen Tulu. 2021. "Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses" Materials Proceedings 3, no. 1: 14. https://doi.org/10.3390/IEC2M-09257
APA StyleWoo, S., O’Neal, D. L., Atnaw, S. M., & Tulu, M. M. (2021). Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses. Materials Proceedings, 3(1), 14. https://doi.org/10.3390/IEC2M-09257








