A Comparative Assessment of XFEM and FEM for Stress Concentration at Circular Holes near Bi-Material Interfaces ^†

Abstract

Accurately predicting stress concentration factors (SCFs) is essential for assessing the structural integrity of components containing holes or discontinuities, especially in multi-material systems. Traditional Finite Element Method (FEM) models often require substantial mesh refinement near geometric discontinuities, whereas the Extended Finite Element Method (XFEM) allows discontinuities to be represented independently of the mesh through enrichment functions. This study provides a comparative assessment of FEM and XFEM for evaluating SCFs around a circular hole located near a bi-material interface. Both methods are implemented in MATLAB R2019a using the level-set approach to describe the hole. The displacement and stress fields obtained from FEM and XFEM are compared, followed by an evaluation against an established analytical reference solution. The findings show that while both methods reproduce global fields with good agreement, differences arise in the accuracy of SCF prediction. These results highlight the conditions under which XFEM may offer advantages over conventional FEM when modeling discontinuities in heterogeneous materials.

1. Introduction

Holes, inclusions, and other geometric discontinuities located near material interfaces are common in composite structures, adhesively bonded joints, and multi-material components. Such discontinuities can generate steep stress gradients and localized concentration effects that may lead to premature failure. The Finite Element Method (FEM) is widely used for analyzing stress fields in these systems, but its accuracy near discontinuities typically depends on mesh conformity and refinement, which can increase modeling effort when the geometry changes or when discontinuities lie close to interfaces [1,2,3,4].

The Extended Finite Element Method (XFEM), developed within the partition-of-unity framework, provides an alternative approach in which discontinuities are incorporated through enrichment functions. When combined with the level-set method, XFEM enables holes or inclusions to be embedded independently of the underlying mesh, potentially reducing the need for mesh adaptation [5,6,7,8,9].

The objective of this study is to systematically compare FEM and XFEM for the specific case of a circular hole positioned near a bi-material interface under uniaxial tension. Instead of assuming the superiority of either method, the comparison focuses on displacement fields, stress distributions, and the accuracy of the resulting stress concentration factors (SCFs) relative to analytical benchmarks. Through this evaluation, the study aims to clarify the applicability and potential advantages of XFEM in problems involving discontinuities within heterogeneous material systems [10,11].

The presence of holes, voids, or inclusions near material interfaces is common in composite laminates, adhesively bonded joints, and multi-material components. Such configurations generate severe stress gradients that can initiate failure [12,13,14,15,16]. The traditional Finite Element Method (FEM) has been the standard tool for stress analysis [1], but its accuracy near discontinuities depends heavily on mesh conformity and local refinement, which becomes particularly cumbersome when the hole is close to a bi-material boundary.

The Extended Finite Element Method (XFEM), introduced by Moës et al. [17] and further developed for holes and inclusions using level sets [3,18], overcomes this limitation by enriching the approximation space with discontinuous functions within the partition-of-unity framework [2,4,5,6,7,8,18]. This allows a fixed, non-conformal mesh to represent complex internal geometries accurately.

This paper directly compares XFEM and conventional FEM for the specific problem of a circular hole located near a bi-material interface under uniaxial tension. The primary objective is to quantify the superiority of XFEM in predicting the stress concentration factor (SCF)—the parameter of greatest engineering importance in such configurations [19].

2. Numerical Methodology

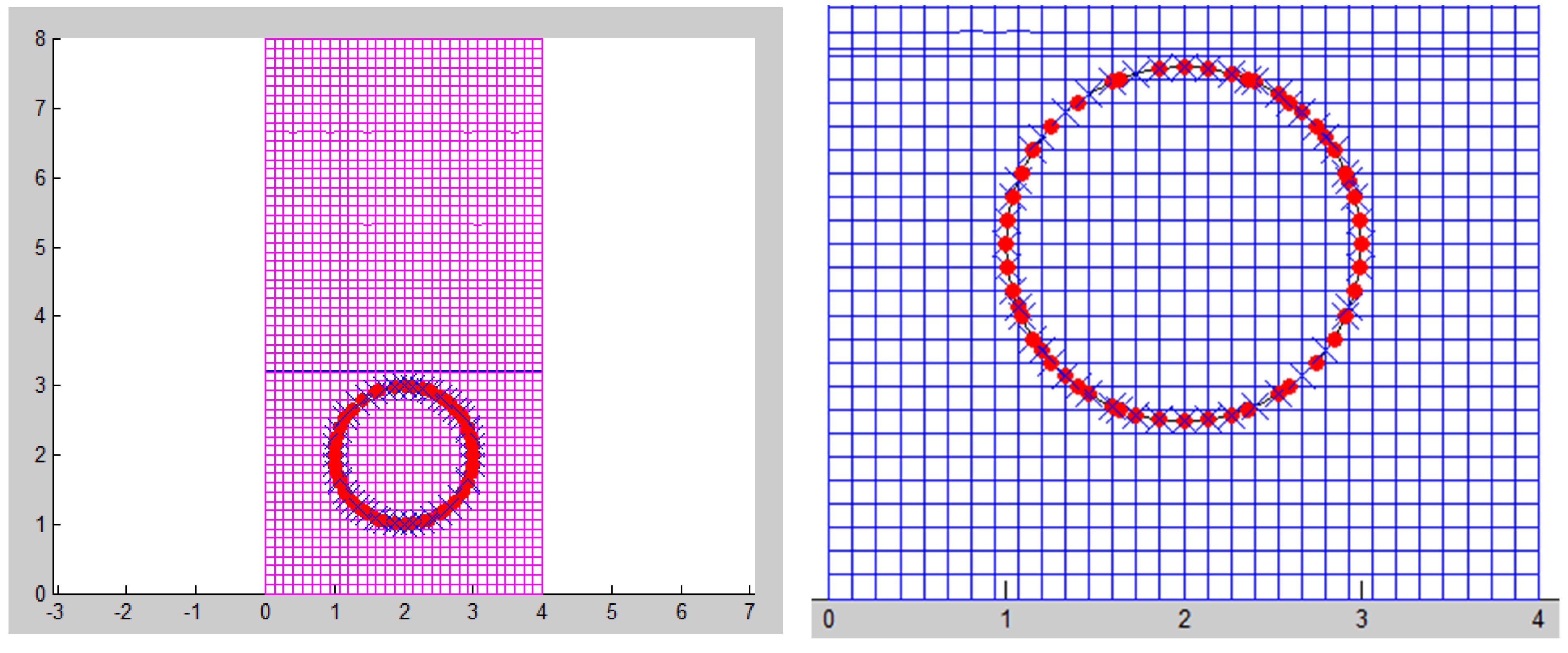
2.1. Geometric Representation via the Level Set Method

Following Sukumar et al. [3,18] and Osher and Sethian [9], the circular hole is described by a level set function φ(x) = ||x − x₀|| − R, where negative values indicate the interior of the hole. Nodal level set values are interpolated using standard shape functions [3].

In this function:

$\mathbf{x}=(x,y)$: spatial coordinate;

${\mathbf{x}}_0=(x_0,y_0)$: center of the circular hole;

$R$: radius of the hole;

$\phi \left(\mathbf{x}\right)<0$: inside the hole;

$\phi \left(\mathbf{x}\right)=0$: hole boundary;

$\phi \left(\mathbf{x}\right)>0$: outside the hole.

2.2. XFEM Formulation for a Hole

Nodes whose support is cut by the hole boundary are enriched with a shifted Heaviside function H(φ(x)) [3,5].

The displacement approximation becomes:

$${\mathrm{u}}^{\mathrm{h}}\left(\mathrm{x}\right)=\mathsf{\Sigma }{\mathrm{N}}_i\left(\mathrm{x}\right){\mathrm{u}}_i+\mathsf{\Sigma }{\mathrm{N}}_j\left(\mathrm{x}\right){\mathrm{a}}_j\mathrm{H}(\phi (\mathrm{x}\left)\right)$$

where ${\mathrm{a}}_j$ are additional degrees of freedom [2,3,4,5,6,7,8,17,18,19].

$N_i\left(\mathbf{x}\right)$: standard finite element shape function.

$I$: set of all nodes in the mesh.

$J\subset I$: set of enriched nodes whose support is intersected by the hole boundary.

${\mathbf{u}}_i=(u_i,v_i)$: standard displacement degrees of freedom.

${\mathbf{a}}_j=(a_j^{\left(u\right)},a_j^{\left(v\right)})$: enriched degrees of freedom accounting for the displacement discontinuity across the hole boundary.

$H(\phi (\mathbf{x}\left)\right)$: shifted Heaviside enrichment function used to enforce traction-free conditions on the hole boundary.

Heaviside function:

$$H(\varphi )=\left\{\begin{array}{c}+1,\phi >0\\ -1,\phi <0\end{array}\right.$$

2.3. Problem Setup

An 8000 × 4000 mm rectangular plate consisting of two perfectly bonded isotropic materials is subjected to uniform tensile stress σ = 1 MPa on the top and bottom edges (Figure 1). Material 1 (bottom): E₁ = 200 GPa; ν₁ = 0.3. Material 2 (top): E₂ = 70 GPa; ν₂ = 0.33. A circular hole of radius r = 1000 mm is placed 6000 mm from the vertical interface. Plane stress conditions are assumed. The analytical SCF for an infinite plate with a central hole is 3, but near an interface and with finite width (D/r ≈ 4), the reference SCF is approximately 2.02 [19].

3. Results and Discussion

Both methods used four-node quadrilateral elements. The FEM model employed a highly refined conformal mesh (≈58,000 elements), whereas the XFEM model used a coarse structured mesh (≈6200 elements) with enrichment only (Figure 2).

It should be noted that, although the global σ_xx stress patterns obtained by XFEM are in good qualitative agreement with FEM, a local sign inconsistency appears at the hole interface. For a plate subjected to uniaxial tension σ_yy, the theoretical solution predicts compressive σ_xx stresses at the top and bottom of the hole and tensile σ_xx stresses at the lateral sides. While this behavior is correctly captured by the conventional FEM results, the XFEM σ_xx contour exhibits a local tensile region at the top of the hole. This discrepancy is attributed to limitations in the stress recovery procedure for the σ_xx component in the enrichment zone of the present XFEM implementation and indicates that XFEM stress fields near the hole boundary should be interpreted with caution.

Qualitatively, all contour plots (Figure 3, Figure 4 and Figure 5) from the two methods are nearly indistinguishable, confirming the ability of XFEM to reproduce global displacement and stress fields accurately despite the non-conformal mesh.

The most significant difference appears in the SCF. Using the well-established analytical benchmark of 2.02 for this geometry [19], XFEM yields an error of only 4.19%, whereas FEM over-predicts by 14.11% (

Table 1. Summary of quantitative comparison.

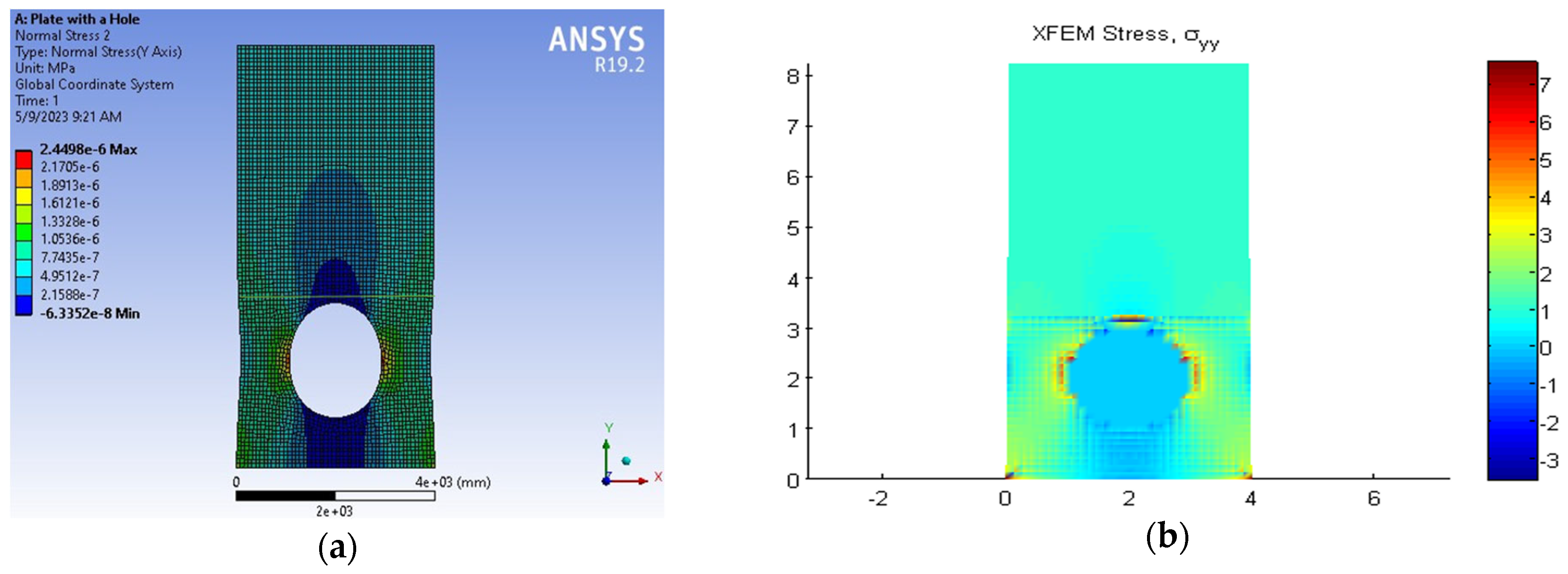
Quantity	FEM	XFEM	Difference (%)
Max ($u_y$) (mm)	0.0719	0.0718	0.14
Max (${\sigma }_{xx}$) (MPa)	3.18	3.15	0.94
Max (${\sigma }_{yy}$) (MPa)	2.37	2.31	2.53
SCF (=${\sigma }_{yy,max}/\sigma$)	2.37	2.31	–
Error vs. analytical (%)	14.11	4.19	–

). This superior accuracy arises because XFEM exactly enforces the traction-free condition on the hole boundary through enrichment, while even a very fine conformal FEM mesh introduces slight geometric approximation errors near curved boundaries [3,5,18].

The computational cost of XFEM was approximately 65% lower than the refined FEM due to the simple structured mesh and absence of local refinement. These advantages become even more pronounced in parametric studies or when the hole position is varied—situations that would require complete remeshing in standard FEM [17,18].

4. Conclusions

This study demonstrates that XFEM significantly outperforms traditional FEM in predicting stress concentration factors around circular holes near bi-material interfaces. While both methods produce comparable global fields, XFEM delivers an SCF error of only 4.19% against the analytical solution [19], compared to FEM’s 14.11%. Combined with its mesh-independent character and lower computational cost, XFEM is established as the preferred numerical tool for discontinuity problems in heterogeneous material systems.