1. Introduction
According to recent studies, nearly 100 billion food cans and 230 billion beverage cans are fabricated worldwide every year [
1,
2]. These figures are continually increasing, especially with the rapidly expanding markets in Asia, the Middle East, and South America. As there is a high production volume and competition amongst can manufacturers, it is necessary for producers to calculate very accurately the total cost of a single can. Even the slightest increase or decrease in the cost of a single can as a result of a manufacturing change can greatly impact the economy for can makers.
Metal cans for beverages that are manufactured in Europe and Asia are typically 45% aluminum and 55% steel alloy, whereas practically all cans in U.S.A. are made entirely of aluminum. However, most food containers are manufactured from steel stock.
There are several processes involved in the transformation of a coil made of metal into a can: blanking, ironing, deep drawing, seaming, doming, necking, and redrawing. Of all these processes, ironing is perhaps the most critical operation in forming the body of the can because of the extremely high pressures, strains, and strain rate associated with this manufacturing step. The punch, which is precisely dimensioned, holds and pushes the cup through two or three carbide ironing rings (
Figure 1). The punch speed is greater than that of the metal through the ironing zone, thus causing the desirable elongation and thinning of the can during the process. The thickness of the metal is greater than the clearance between each ring and the punch. The punch surface generates friction that subsequently facilitates the metal being pushed through the ironing rings.
To remove any residual toxic lubricants and apply a thin layer of polymer to the base metal, cans are cleaned with water between the doming and necking processes. A spray is applied to the cans to ensure a high-quality surface for the contents of the can. However, when the substances in this spray are boiled, volatile organic compounds can (VOC) result due to the presence of polymer resins such as methyl ethyl ketone. These resulting volatile organic compounds raise numerous health and environmental concerns, and the canning industry has the elimination of VOC in the production process as its purpose.
Thermoplastic pre-coated rolled steels have proven to be a suitable alternative for base stocks in the can manufacturing process previously described. These steels are heated first, and then compacted between some polymer sheets. After this step, the resulting sheets are quenched to proportionate a very strong bond between the steel base and the polymeric layers. These new types of coated steels were studied by Jaworski et al. [
4], finding that they can be perfect materials for the forming process if some variables were controlled carefully. The polymer layers also have an advantage to serve as solid lubricants, as well as having the potential to remove VOCs during the manufacturing process.
A new polymer coated steel with multiple layers, developed for use in food and beverage industries, is an extension of research previously conducted on polymer coated steels in forming processes. This new material presented has several advantages over preceding materials, including:
Maximizing steel–polymer interface adhesion by appropriately selecting the polymer.
A desired permeability can be implemented on the exterior surface, which can aid in decoration.
Formability may be increased by modifying the mechanical properties of the polymer layers.
Different design objectives are possible by altering the thickness of each layer.
Any fractures of de-lamination of the polymer laminates can lead to subsequent corrosion and spoilage of the contents; therefore, this new material is only useful if it is not damaged during all the forming stages of can manufacturing. To generate the new surface, high pressures, strains, and strain rates occur during ironing.
2. Materials and Methods
2.1. Material
The material has been provided by ArcelorMittal (Chicago, USA). The innovative steel coated with two polymer layers in both the punch and die sides is illustrated in
Figure 2. The two layers are the tie layer, which is the layer that bonds the steel substrate to the top layer, in the external part, both with a standard total thickness ranging from 12.5–35 μm. For precise measurement of the polymer layers, Wagner’s dis-indentation method can be used [
5]. These polymeric layers can be adapted to any conditions.
2.2. Experimental Procedure
A trip ironing simulator was used for experimental investigation.
Figure 3 shows five frames showing the exact moment the ironing simulator irons a strip. This device was developed at the University of Notre Dame. Basically, it has a punch where a metal strip can be attached using a bolt. Then, with the help of a 22 kW motor, the punch moves to the left forcing the strip to pass through the small space that exists between the punch and the die, which is smaller than the total thickness of the workpiece. This movement reproduces the basic principle of the ironing process, which is the most critical one in can manufacturing due to the high stresses involved. The maximum punch speed that is possible to get with this device is 2 m/s.
Under numerous testing conditions, the two-layered polymer material displayed excellent ironability. A design-of-experiments was prepared and the parameters that were varied include the punch velocity, die angle, thickness reduction, and the die temperature. The two expected results of the experiments are: good ironing process or bad result (one or two polymer layers have been damaged).
2.3. UBM Models
In order to accurately predict possible outcomes of an ironing process that uses multi-layered polymer steel coatings, a good theoretical model must be developed. Although the Finite Element Method (FEM) is most commonly employed by researchers [
6,
7,
8,
9,
10], this is hard to apply for predictive models. The Upper Bound Method (UBM) is known methodology that also accurately models real processes, and is preferred by some researchers [
11,
12,
13].
With the UBM, it is assumed that the given material experiences any required deformations necessary to achieve the final desired shape under a kinematically admissible flow field [
14]. The principal issue encountered with use of UBM is the a priori displacement assumption needed, but this can usually be overcome by using values calculated from the slip line theory, from experimental data, or intuition.
For the research presented here, there are two possible outcomes that can occur: an ironing with success or an ironing with a shaving condition. If this one is present, the material is damaged as result, and any of the following effects will also take place: the top polymer layer is only damaged, or both the top and tie polymer layers are damaged.
Two UBM models have been developed for each of the two possible results: good ironing or shaving condition. Damage at the two layers of the polymer requires more power than that necessary to cause damage only at the external layer of a given polymer, and the models include various assumptions used primarily for simplification.
These assumptions are that the material is assumed to be rigid and that the solids are completely plastic. However, it is strange that a polymer behaves like these assumptions; the material rarely acts entirely plastic. However, a certain number of shear planes is essential to enhance the accuracy of the power estimations. Challen et al. [
15] proposed the theory of an operational shear strength for the polymer, which would allow for improved accuracy in the application of the model of strength. It is described as
where
k is the shear stress,
is the shear strain, and
is the shear strength. The polymer shear strength,
, is described as a portion of the whole piece shear strength,
, in both models presented in this work.
There is a unique friction factor associated with each interface. The punch-piece boundary is represented by , the metal-tie layer boundary by , the tie-top layers boundary by , and, lastly, is the friction at the die-top layer boundary. The ironing process will be ignored because tests have determined that the coating on the punch side of the sheet persists all the time during this process.
2.3.1. Model for Ironing
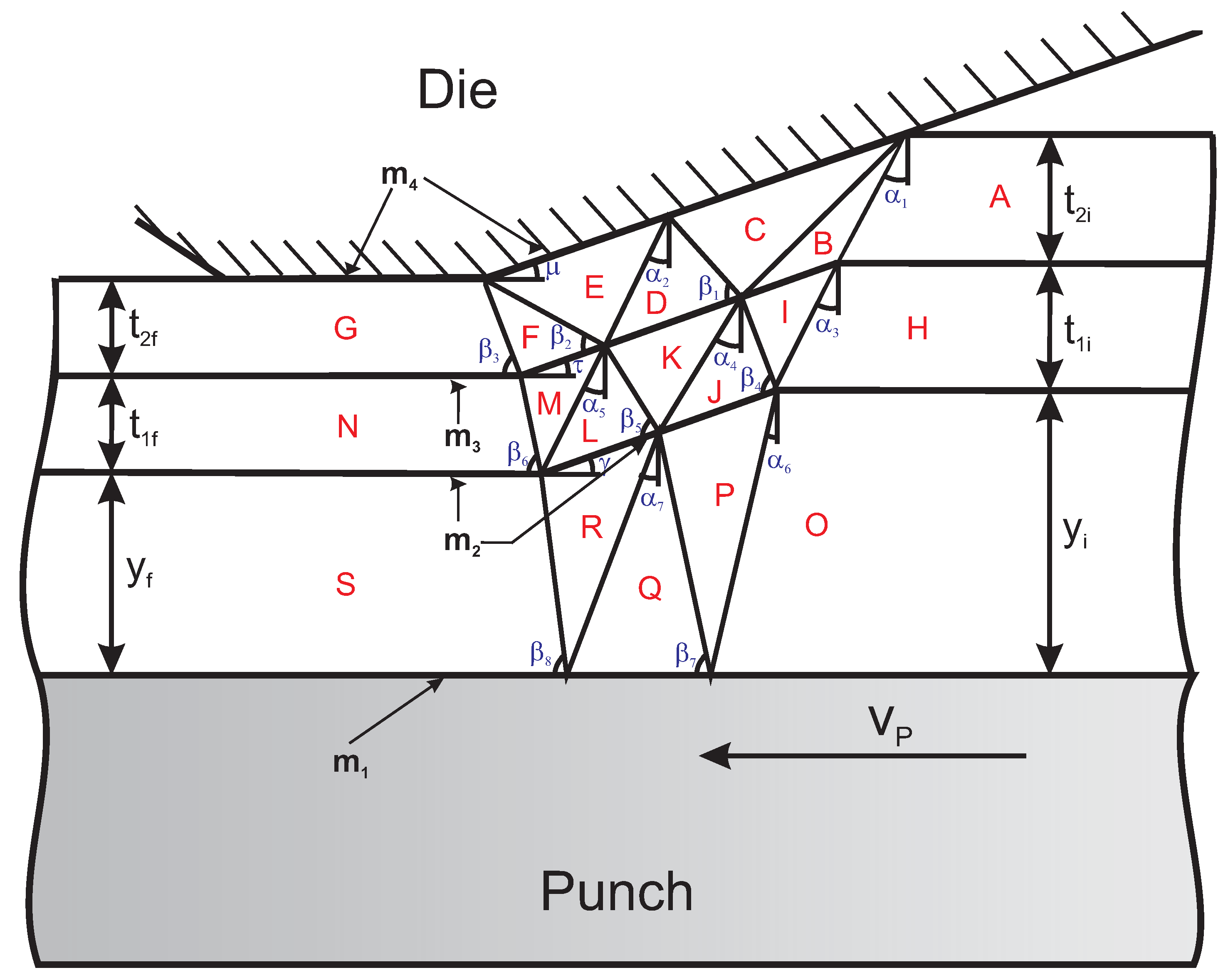
Figure 4 illustrates the velocity discontinuity field (VDF) associated with the successful ironing process involving the new coated steel. The plane Die-G is supposed to continue throughout the entire land length.
The angles – and – have an influence on the deformation planes, including the specified reduction and the angles (die angle), , , and .
2.3.2. Model for Shaving
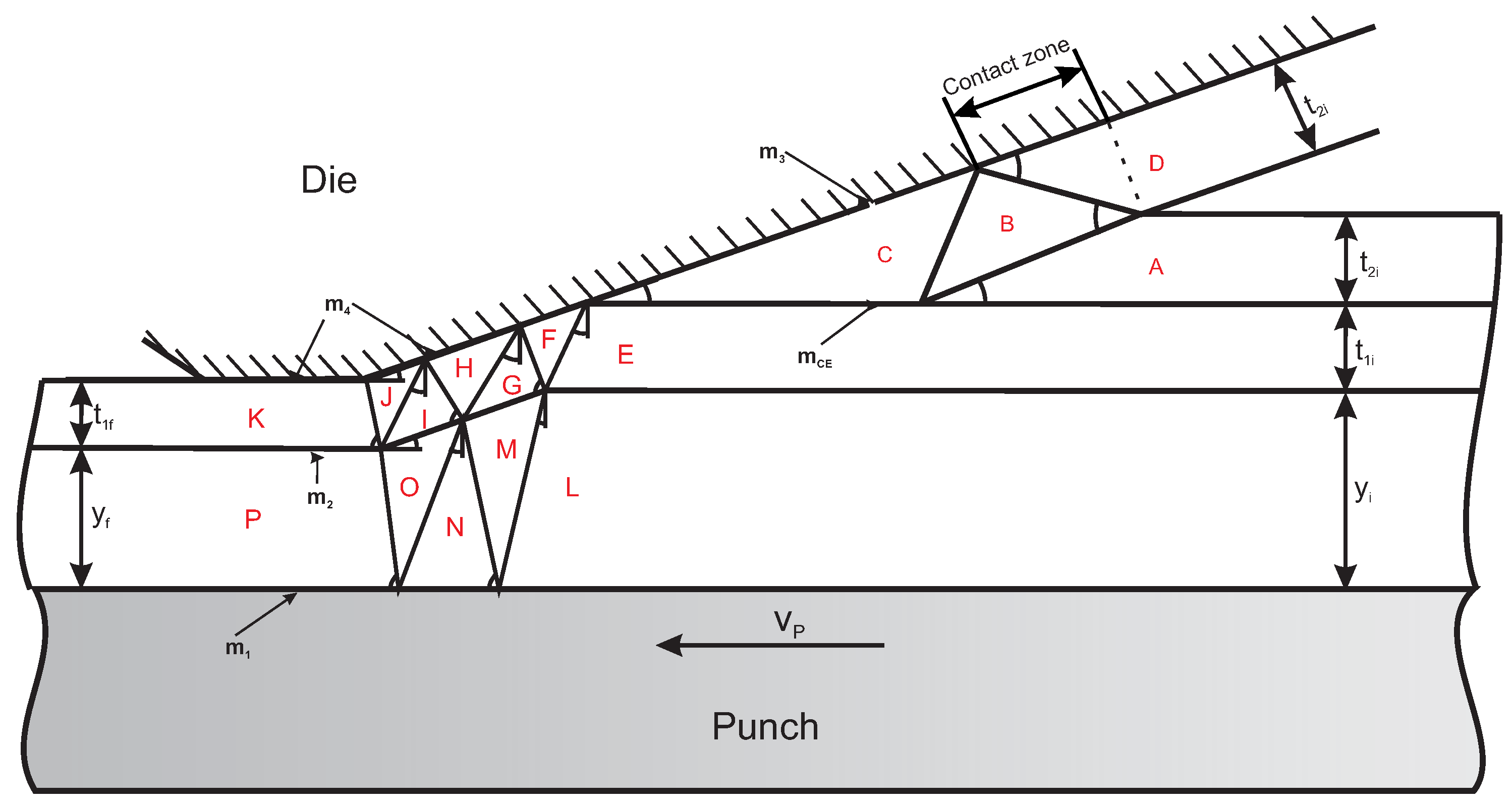
Figure 5 presents the VDF associated with a bad ironing process.
The layer that has been removed as result of shaving is region D, and its initial and final thicknesses are the same. An estimate is used for the area of interaction between the die and this layer because the real area is particularly complicated to determine. Using the approach presented by Wilson [
16], the contact length between the die and region D is also depicted in
Figure 5.
2.4. Artificial Neural Network
The ironing process has also been modeled with Artificial Intelligence (AI), creating an Artificial Neural Network (ANN) for that purpose. This consist of process elements or neurons arranged in columns or layers. Each neuron is only able to do a simple task. They are connected among them with different weights. The first layer is the input layer, while the last one is the output layer. It is possible to have several layers between these two basic layers, and they are known as hidden layers. If there are many hidden layers, then the ANN is called a deep neural network (DNN) [
17]. The ANN will be trained once the weights have the best possible value, then obtaining a really low error.
The ANN has been developed using the commercial software JustNN©. In order to make the ANN training, the algorithm selected has been the Back Propagation (BP).
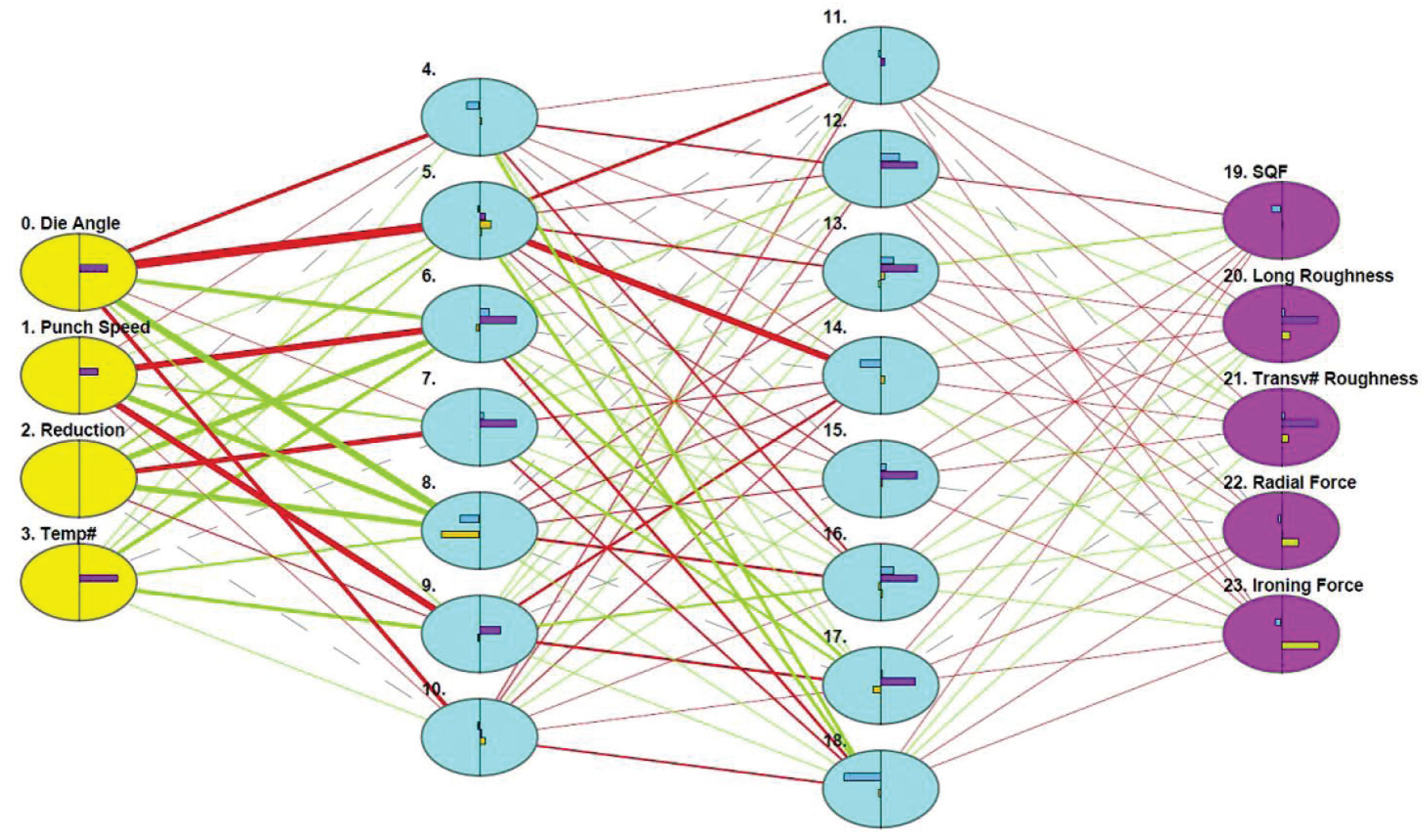
Table 1 shows the variables used in the ANN. The SQF (Surface Quality Factor) output variable is a qualitative value, depending upon the visual aspect of the surface (data have been taken from experimental results).
After 76,315 training cycles, it has been possible to get the optimal neural network, which is represented in
Figure 6. It has four layers (input, two hidden layers, output), and a total of 342 connections. The estimated error is
.
3. Results
3.1. Theoretical Results
3.1.1. UBM Models Results
Results vary depending on whether the successful ironing model is implemented or if the shaving model is. The deformation mode requires less power dissipation, and the UBM indicates that this rule will be followed by the current process. A comparison between the resulting curves for the ironing and shaving models will indicate the preferred mode for a given set of conditions.
Whenever possible, a non-dimensionalized form of the process input power has been implemented as ; P is the total power required, k is the strip shear strength, a is the strip width, is the workpiece thickness at the beginning of the process, and is the punch speed. The variable inserts allow for different process geometries to be tested.
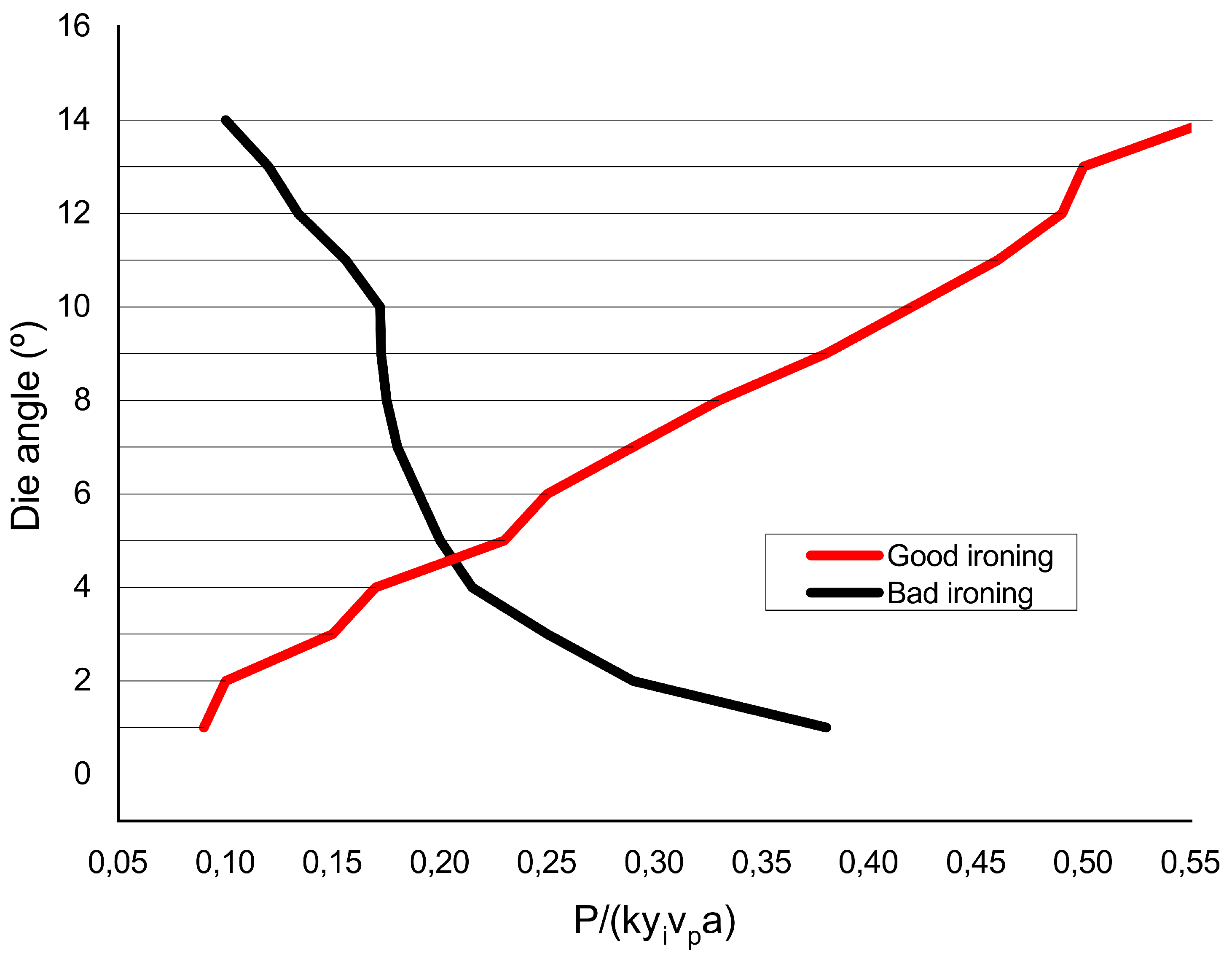
A comparison between shaving and ironing conditions of die angle vs. optimal power curves can be seen in
Figure 7. Below the angle
, a good ironing process will need less power consumption, by the UBM, thus making it the favorite mode with these conditions. Above the angle
, shaving will need less power and will then be the favorite mode. From a formability standpoint, the critical angle,
, is of great importance because it will influence the die geometries that will be necessary for successful ironing of this new material.
3.1.2. ANN Results
The software used to generate the ANN can also provide interesting analysis data. Sensitivity analysis has been defined as “the study of how the uncertainty in the output of a model can be apportioned to different sources of uncertainty in the model input” [
18]. That is, sensitivity analysis evaluates how an output variable reacts to changes of the input variables. For an optimal output model of good ironing,
Table 2 shows the values of the sensitivity analysis for each input variable.
The most important input variable to the model is die angle, as shown in
Table 2. Few variations on this angle will produce big differences on output variables. Punch velocity has also an essential importance. This will give insight into which variable to focus on when manufacturing cans with this new material.
3.2. Experimental Results
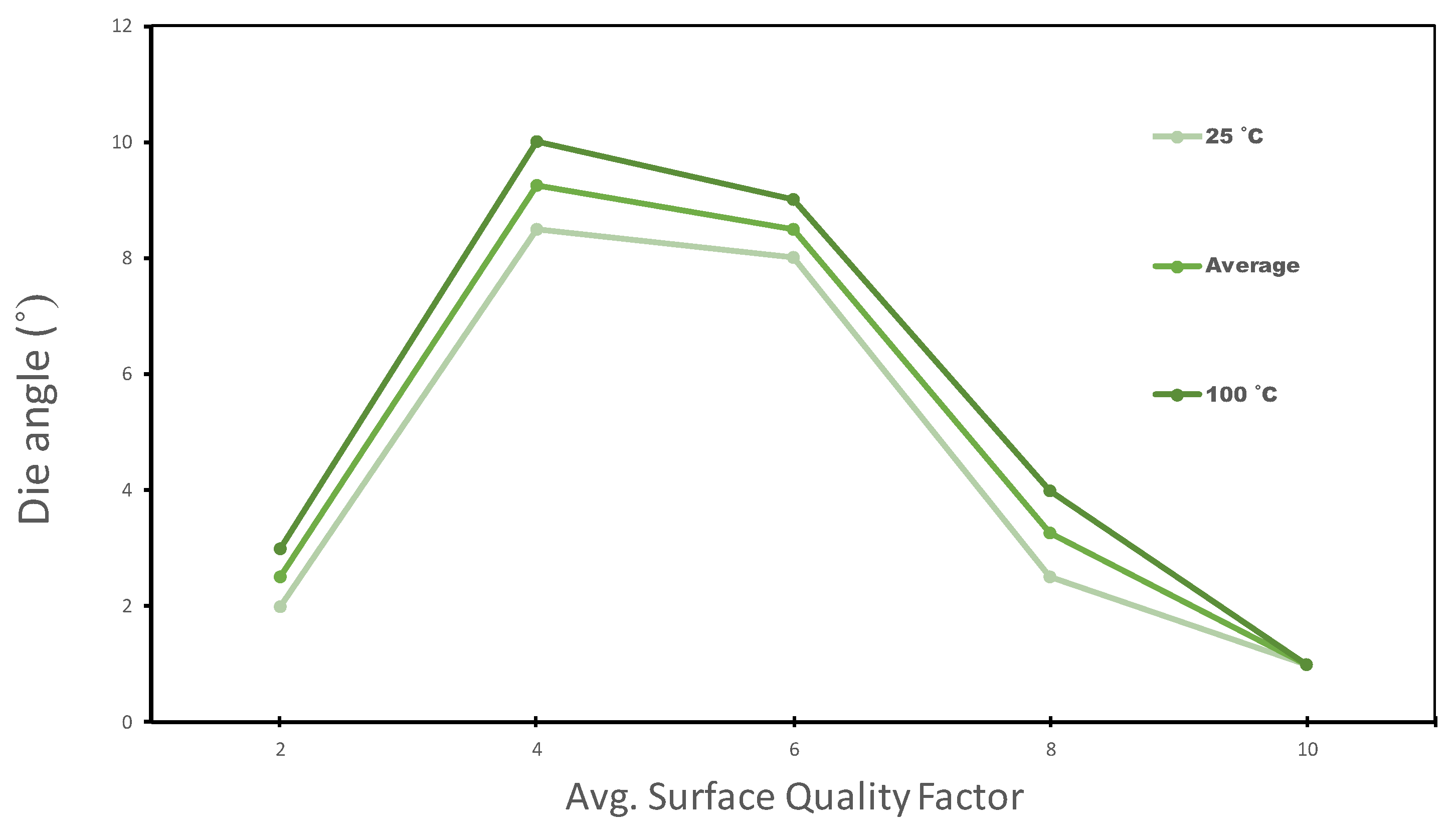
The Surface Quality Factor (SQF) is a qualitative measurement that shows how good the top polymer layer surface is after the ironing process. A value of 10 indicates that the surface is perfect, and decoration can be applied perfectly on it. A value of 0 means that the top layer has completely been destroyed in the process.
Figure 8 shows the SQF observed values versus die angle. As the die angle increases, the occurrence of shaving becomes more frequent, and the SQF has high values at angles close to
. The SQF also improves with high temperatures, as seen in
Figure 8; however, this difference is negligible.
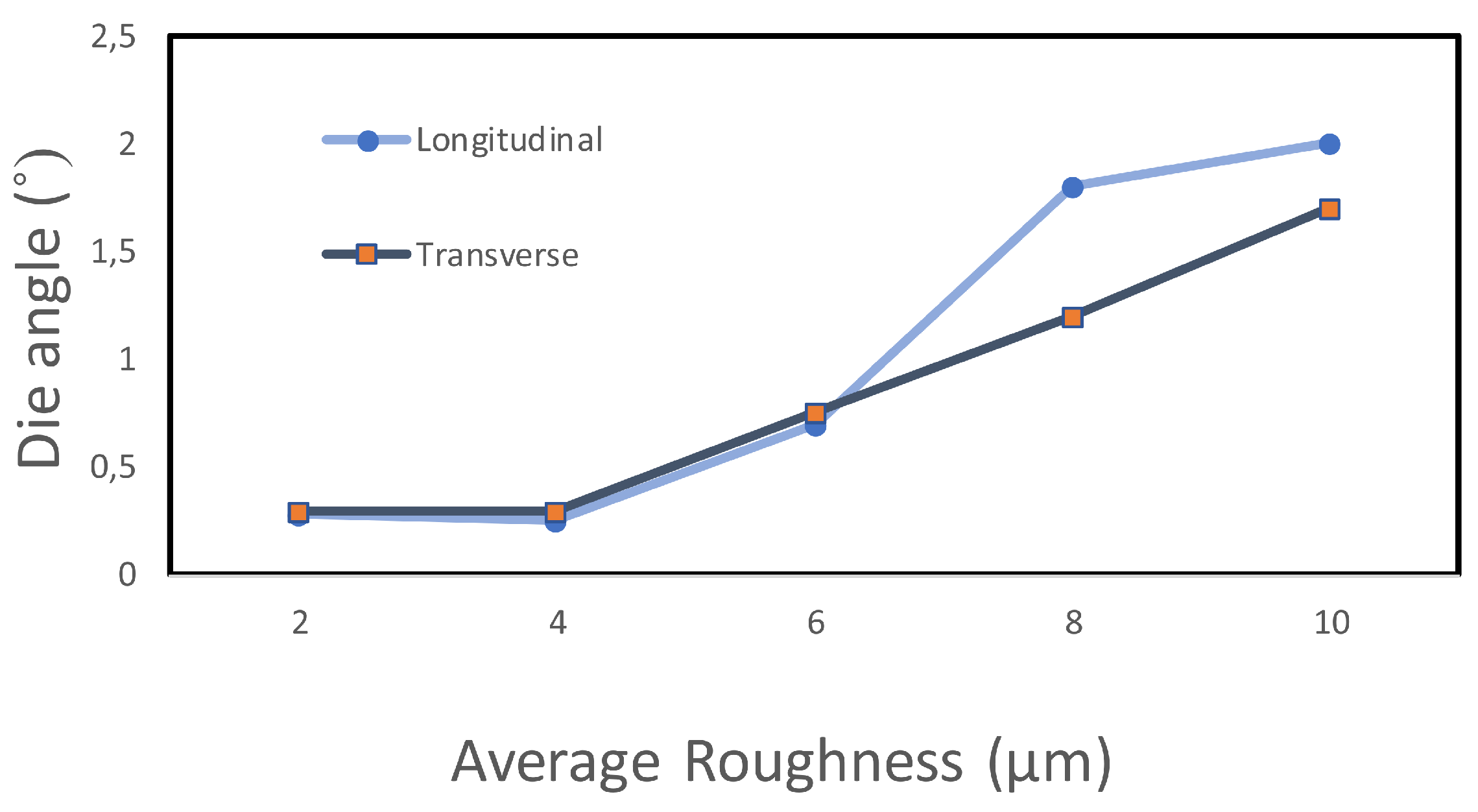
The surface roughness of the specimens was also measured in two directions (transverse and longitudinal). When looking at the roughness in
Figure 9, there is a major correlation between longitudinal roughness and die angle (ironing direction) compared to the transverse roughness. As confirmed in
Figure 8, during the transition from
to
, the roughness undergoes a significant change. Optimal results are achieved if we choose
for the die angle based on a comparison and analysis of
Figure 8 and
Figure 9.
In the experiments conducted for this study, a bad result in the process did not produce a removal of the tie layer for the material. If higher reductions in thickness are investigated, however, these results may differ.
In order to analyze the importance of the process variables, an analysis of variance has been done. As summarized in
Table 3, the most critical factor is die angle, which is coherent with the sensitivity analysis provided by the ANN.
As shown in
Table 3, ironing velocity was also influential, with a higher speed producing an improved ironability.
The goal is to achieve the highest possible value of SQF, and this can be accomplished working with elevated temperature and velocity, and with low reductions.
4. Conclusions
This conducted research has demonstrated that it is possible to manufacture cans with this new material because the most critical step (ironing) can result in a successful operation, but always under certain controlled conditions, as described in this document. Therefore, several steps in can manufacturing that produce COVs can be avoided, resulting in an environmental and economical alternative to traditional can manufacturing.
Important data for successful can manufacturing have been found as a result of experimental tests and the development of theoretical models (UBM and ANN). There was a strong correlation between both the experimental and theoretical data, indicating a valid theoretical approximation. It is now possible to begin altering strengths and thicknesses of different coatings, tool angles, or reductions to find the best solution and advise can designers and manufacturers.
The two-polymer coated steel showed good ironability, and the die angle is very important when the material is ironed, as either the experimental or the ANN results indicated. or less are recommendable values for this angle.
The survivability demonstrated by the material to the ironing process indicates that it is appropriate for a good lubricant in the process, and it also provides a good contact surface for a food or beverage container.