Thermal Kinetics of Gold Nanosphere under a Burst of Femtosecond Laser †
Abstract
:1. Introduction
2. Materials and Methods
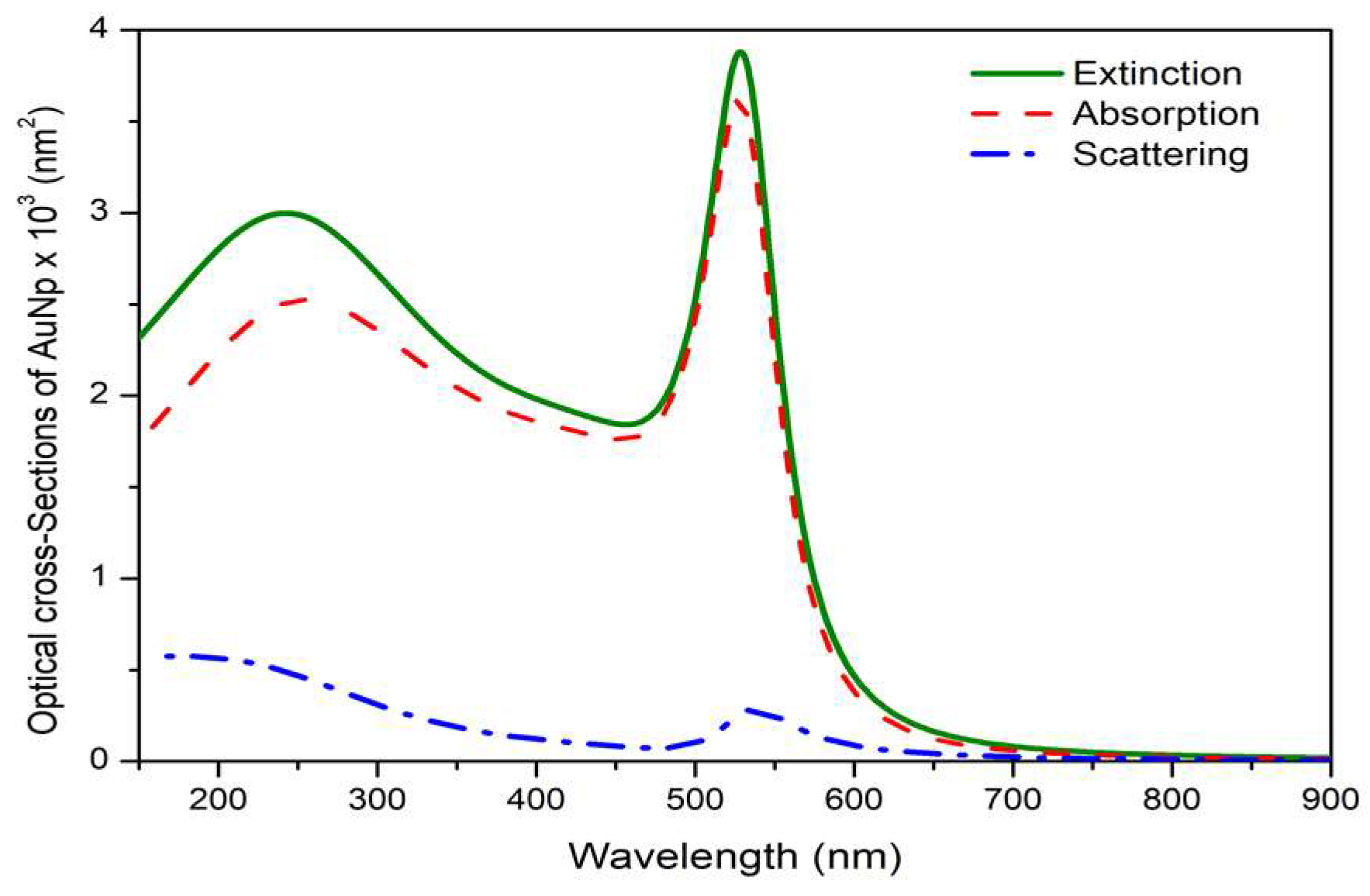
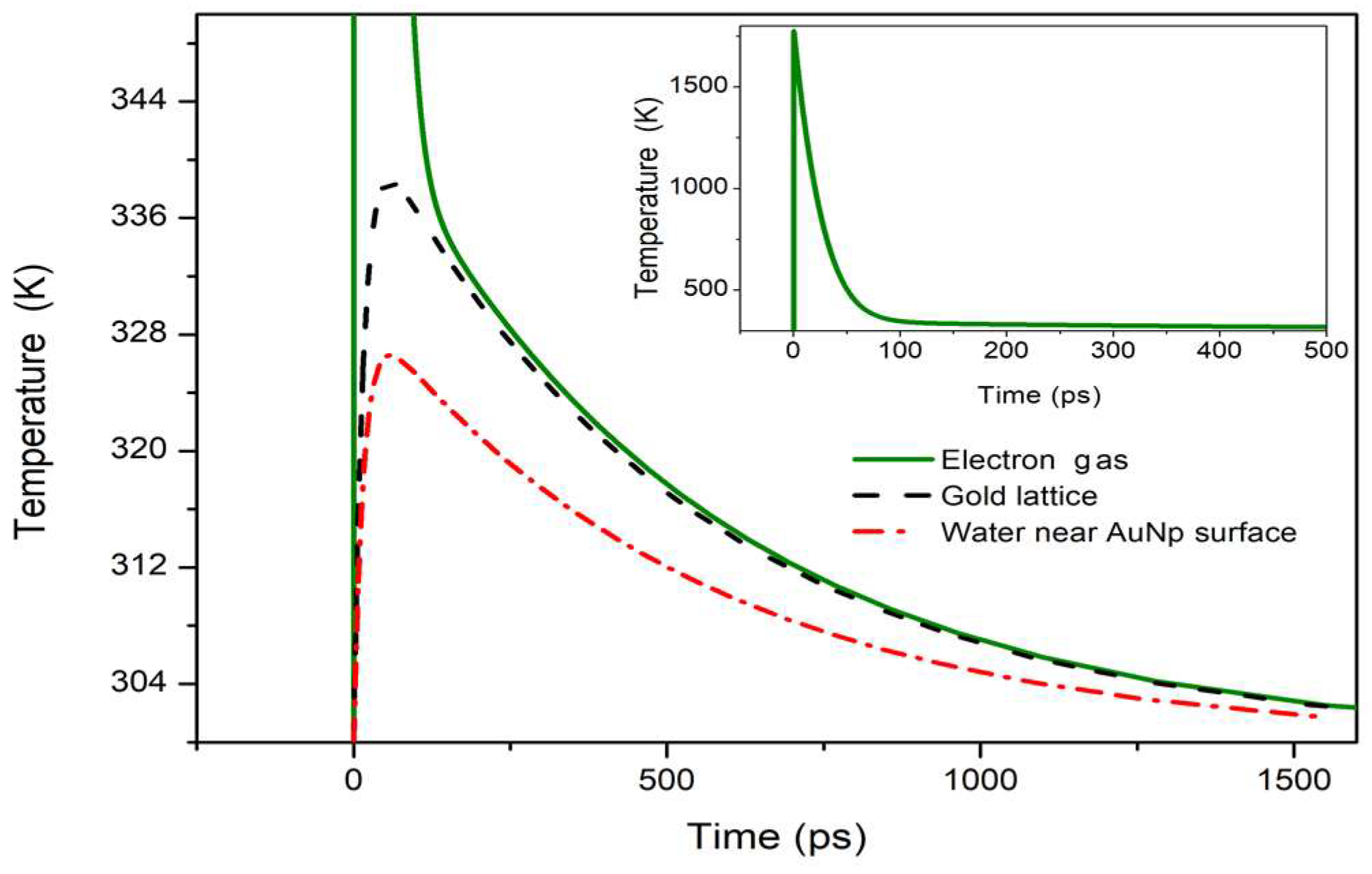
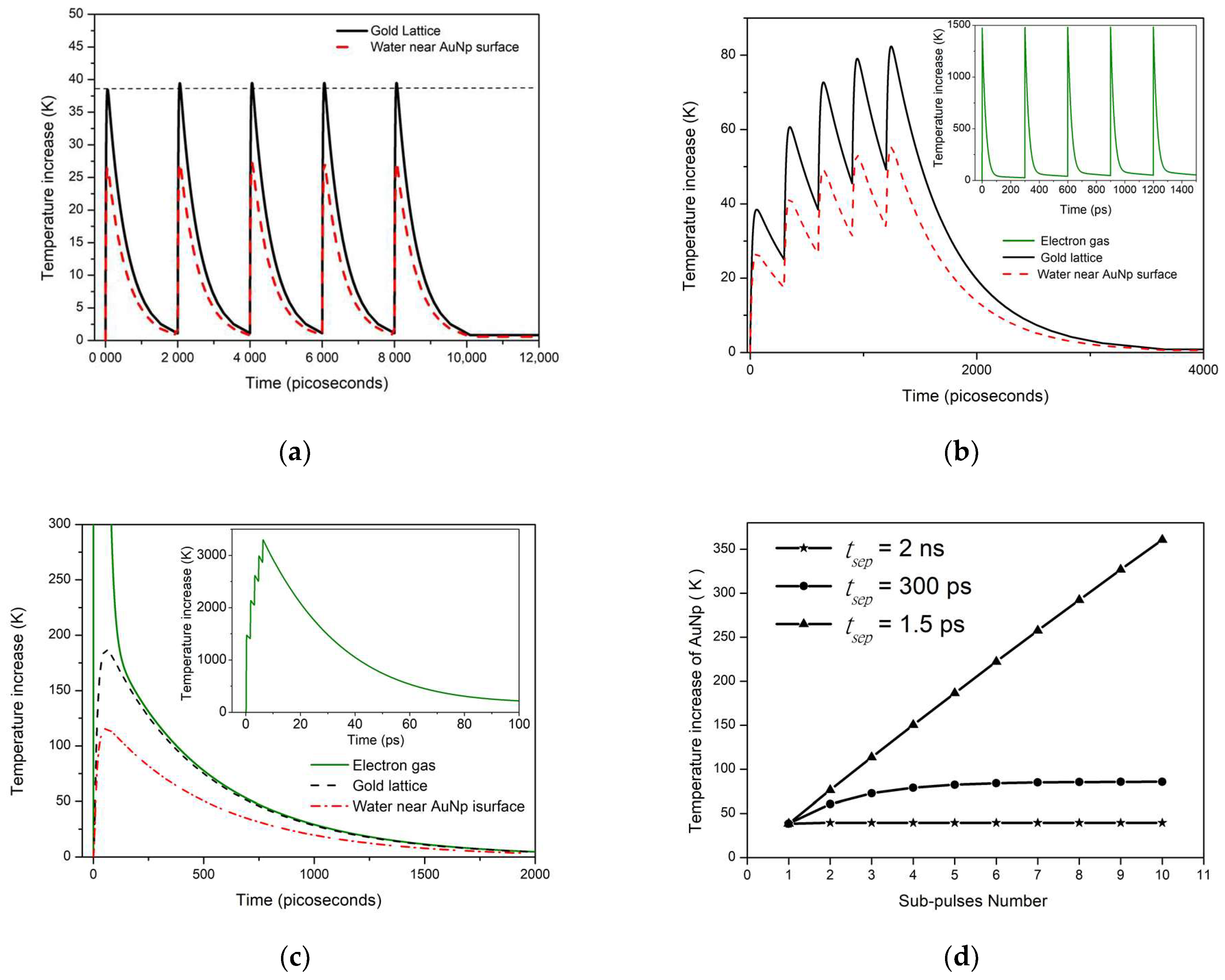
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rout, A.; Boltaev, G.S.; Ganeev, R.A.; Fu, Y.; Maurya, S.K.; Kim, V.V.; Rao, K.S.; Guo, C. Nonlinear Optical Studies of Gold Nanoparticle Films. Nanomaterials 2019, 9, 291. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, H.J.; Du, X.; Wen, D. Photothermal conversion characteristics of gold nanoparticle dispersions. Sol. Energy 2014, 100, 141–147. [Google Scholar] [CrossRef]
- Chang, C.C.; Chen, C.P.; Wu, T.H.; Yang, C.H.; Chii-Wann Lin, C.W.; Chen, C.Y. Gold Nanoparticle-Based Colorimetric Strategies for Chemical and Biological Sensing Applications. Nanomaterials 2019, 9, 861. [Google Scholar] [CrossRef] [PubMed]
- Amina, S.J.; Guo, B. A Review on the Synthesis and Functionalization of Gold Nanoparticles as a Drug Delivery Vehicle. Int. J. Nanomed. 2020, 15, 9823–9857. [Google Scholar] [CrossRef] [PubMed]
- Letfullin, R.R.; Iversen, C.B.; George, T.F. Modeling nanophotothermal therapy: Kinetics of thermal ablation of healthy and cancerous cell organelles and gold nanoparticles. Nanomed. Nanotechnol. Biol. Med. 2011, 7, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Wrigglesworth, E.G.; Johnston, J.H. Mie theory and the dichroic effect for spherical gold nanoparticles: An experimental approach. Nanoscale Adv. 2021, 3, 3530–3536. [Google Scholar] [CrossRef] [PubMed]
- Draine, B.T.; Flatau, P.J. User guide for the discrete dipole approximation code DDSCAT 7.3. arXiv 2013, arXiv:1002.1505. [Google Scholar]
- Anisimov, I.S.; Kapeliovich, B.L.; Perel’man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Sov. Phys. JETP 1974, 39, 375–377. [Google Scholar]
- Majchrzak, E.; Dziatkiewicz, J. Analysis of ultra-short laser pulse interactions with metal films, using a two-temperature model. J. Appl. Math. Comput. Mech. 2015, 14, 31–39. [Google Scholar] [CrossRef]
- Ekici, O.; Harrison, R.K.; Durr, N.J.; Eversole, D.S.; Lee, M.; Ben-Yakar, A. Thermal analysis of gold nanorods heated with femtosecond laser pulses. J. Phys. D Appl. Phys. 2008, 4, 185501. [Google Scholar] [CrossRef] [PubMed]
- Gan, R.; Fan, H.; Wei, Z.; Liu, H.; Lan, S.; Dai, Q. Photothermal Response of Hollow Gold Nanorods under Femtosecond Laser Irradiation. Nanomaterials 2019, 9, 711. [Google Scholar] [CrossRef] [PubMed]
- Pustovalov, K.V. Theoretical study of heating of spherical nanoparticle in media by short laser pulses. Chem. Phys. 2005, 308, 103–108. [Google Scholar] [CrossRef]
- Volkov, A.N.; Sevilla, C.; Zhigilei, L.V. Numerical modeling of short pulse laser interaction with Au nanoparticle surrounded by water. Appl. Surf. Sci. 2007, 253, 6394–6399. [Google Scholar] [CrossRef]
- Ali, H.; Simon, F.D.; Michel, M. Simulation of nanosecond laser-induced thermal dynamics of hollow gold nanoshells for hyperthermia therapy. AIP Conf. Proc. 2014, 1590, 105. [Google Scholar]
- Carpenter, M.; Kennedy, C.A. Fourth-Order 2N-Storage Runge-Kutta Schemes; NASA: Washington, DC, USA, 1994; p. 24. [Google Scholar]
| Parameter | Value | Ref. |
|---|---|---|
| AuNp | ||
| Electron heat capacity, Ce (Jm−3 K−1) | [12] | |
| Lattice heat capacity, CL (Jm−3 K−1) | [11] | |
| Density, ρgold (Kg m−3) | [12] | |
| Gold melting temperature, Tm (K) | 1337 | [5,11] |
| Water | ||
| Critical temperature, TCr (K) | 647 | [5,11] |
| Boiling temperature, Tb (K) | 3130 | [5,11] |
| Cavitation threshold Tcav (K) | 573 | |
| Thermal conductance at the gold/water interface, G (Wm−2 K−1) | [5] | |
| Thermal conductivity, k∞ at T = 300 K (Wm−1 K−1) | 0.61 | [5] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mediene, S.; Senoudi, A.R. Thermal Kinetics of Gold Nanosphere under a Burst of Femtosecond Laser. Mater. Proc. 2023, 14, 37. https://doi.org/10.3390/IOCN2023-14511
Mediene S, Senoudi AR. Thermal Kinetics of Gold Nanosphere under a Burst of Femtosecond Laser. Materials Proceedings. 2023; 14(1):37. https://doi.org/10.3390/IOCN2023-14511
Chicago/Turabian StyleMediene, Selma, and Assia Rachida Senoudi. 2023. "Thermal Kinetics of Gold Nanosphere under a Burst of Femtosecond Laser" Materials Proceedings 14, no. 1: 37. https://doi.org/10.3390/IOCN2023-14511
APA StyleMediene, S., & Senoudi, A. R. (2023). Thermal Kinetics of Gold Nanosphere under a Burst of Femtosecond Laser. Materials Proceedings, 14(1), 37. https://doi.org/10.3390/IOCN2023-14511






