Robust Optimal Utilization in a Grid-Interfaced PV System Using an Efficient Controller with a GWO Control Strategy ^†

Abstract

Robust optimal utilization was achieved in the integrated module of the grid-interfaced PV system. The module was created by combining a modified series capacitor high conversion ratio (MSC-HCR) converter, a maximum PowerPoint tracker (MPPT), and an efficient controller with a Grey Wolf Optimizer algorithm (GWO). The GWO created a database of control signals for optimal performance and provided the correct control signals for the system. The goal was to achieve stable, optimal power utilization at load, as represented by the system’s data signal in terms of current, voltage, and power. Power banks, such as batteries, can supply consistent and uninterrupted power to the load. The novel control strategy was employed to enhance power at load under optimal conditions. The suggested model was tested in the MATLAB/Simulink environment under a variety of scenarios, and the system’s efficiency was evaluated using existing technologies.

1. Introduction

Renewable energy sources (RES) are the most environmentally friendly options for generating electricity. Solar power has the potential to provide limitless, low-cost electricity [1]. The intermittent nature of PV systems, as well as weather conditions, cause solar power generation to be interrupted. PV systems linked to microgrids can produce enough electricity to meet load demands [2]. A power electronic converter, such as a voltage source inverter (VSI), is commonly used to link DGs to the network [3]. Batteries are commonly used in solar PV systems for providing uninterrupted power to load [4]. In a grid-interfaced system, power management is critical to maintain system reliability [5]. Here, we proposed an MSC-HCR converter which was modelled from an SC-HCR converter to enhance power at the load side [6]. The converter was modelled by using the state-space averaging approach [7] and its performance and stability were analyzed. The MPPT delivers accurate signal data to the PWM unit for optimal switching of the converter [8]. An efficient controller is required to manage the power from the source to the load. In this work, we used the Grey Wolf Optimizer (GWO) algorithm as a control strategy to create an efficient controller [9,10]. The proposed GWO strategy was compared with existing strategies in the MATLAB/Simulink environment. We studied different cases, including changing irradiance under constant load and variable load at constant irradiance. The current, voltage, and power responses for both the cases were investigated and compared with existing techniques such as BSO [10,11], and PSO [12].

The remainder of this project is organised as follows. The architecture of the grid-interfaced solar system is covered in the second section. Section 3 discusses the converter’s modelling and operational modes. Section 4 discusses the methodology of current heuristic optimization methods. Section 5 examines the MATLAB and Simulink results. The present work is concluded in Section 6.

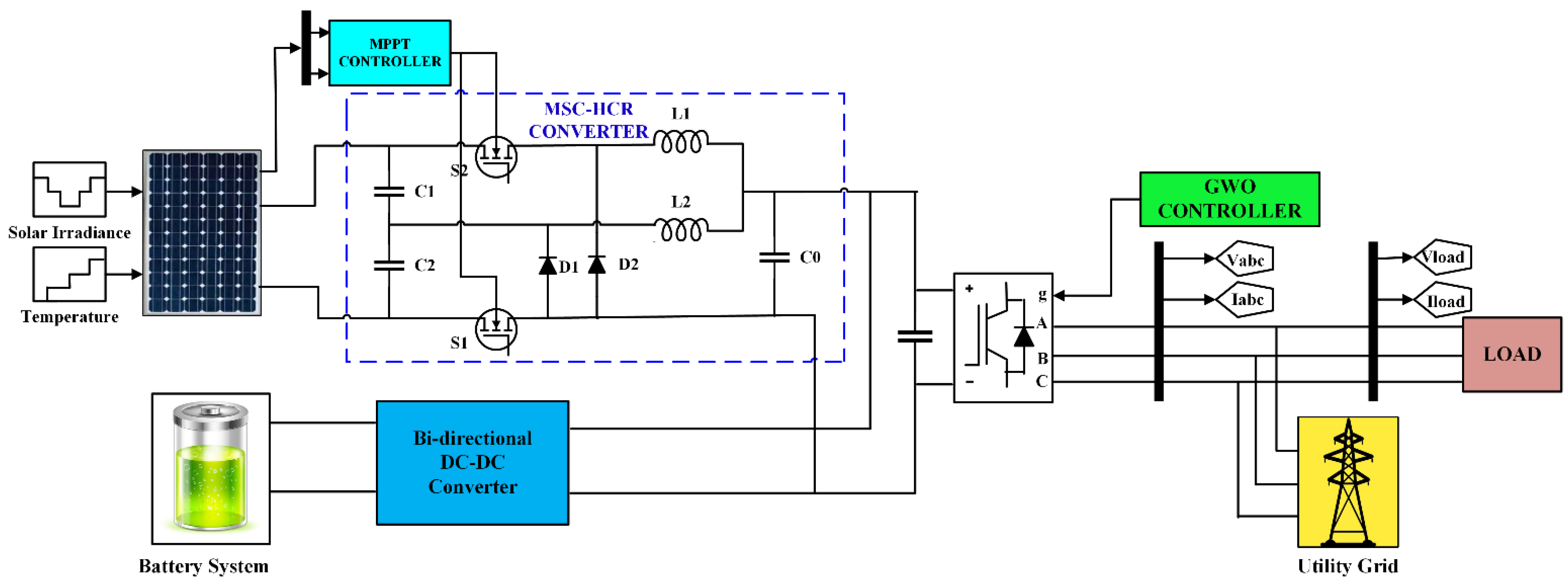
2. Architecture of the Grid-Interfaced PV System

The architecture of the grid-interfaced PV system model is shown in Figure 1. The model contains the grid-interfaced PV, battery, MSC-HCR Converter, GWO based controller, microgrid, and electrical system. The photovoltaic cell generates electricity from light energy using a solar module, which is subsequently transmitted to the DC Microgrid via the DC/DC Converter. The converter output can be controlled by using the MPPT controller. The battery system is connected to the DC-Microgrid through a bi-directional converter. The DC-Bus is linked to the AC-Bus with the help of a DC/AC Converter. If solar energy is available, the solar system is used to generate electricity, and the batteries are charged as well. When solar energy is not available, especially at night, the batteries provide a continuous power supply to the loads.

Photovoltaic System

Solar cells are fundamental units of the solar-power system. The PV modules are designed with a connecting group of PV cells in series and parallel based on the required voltage, current, and power ratings. PV arrays are designed according to the application. The power-delivery capacity of the PV system depends on the temperature and irradiance. The MPPT is used to increase efficiency by tracking the maximum energy from the solar system. An effective algorithm is essential for MPPT to track maximum power. Here, we adopted the most popular P&O MPPT algorithm because of its simplicity, effectiveness, and suitability with the system. The P&O MPPT approach was used to manage the duty cycle of the MSC-HCR converter [6].

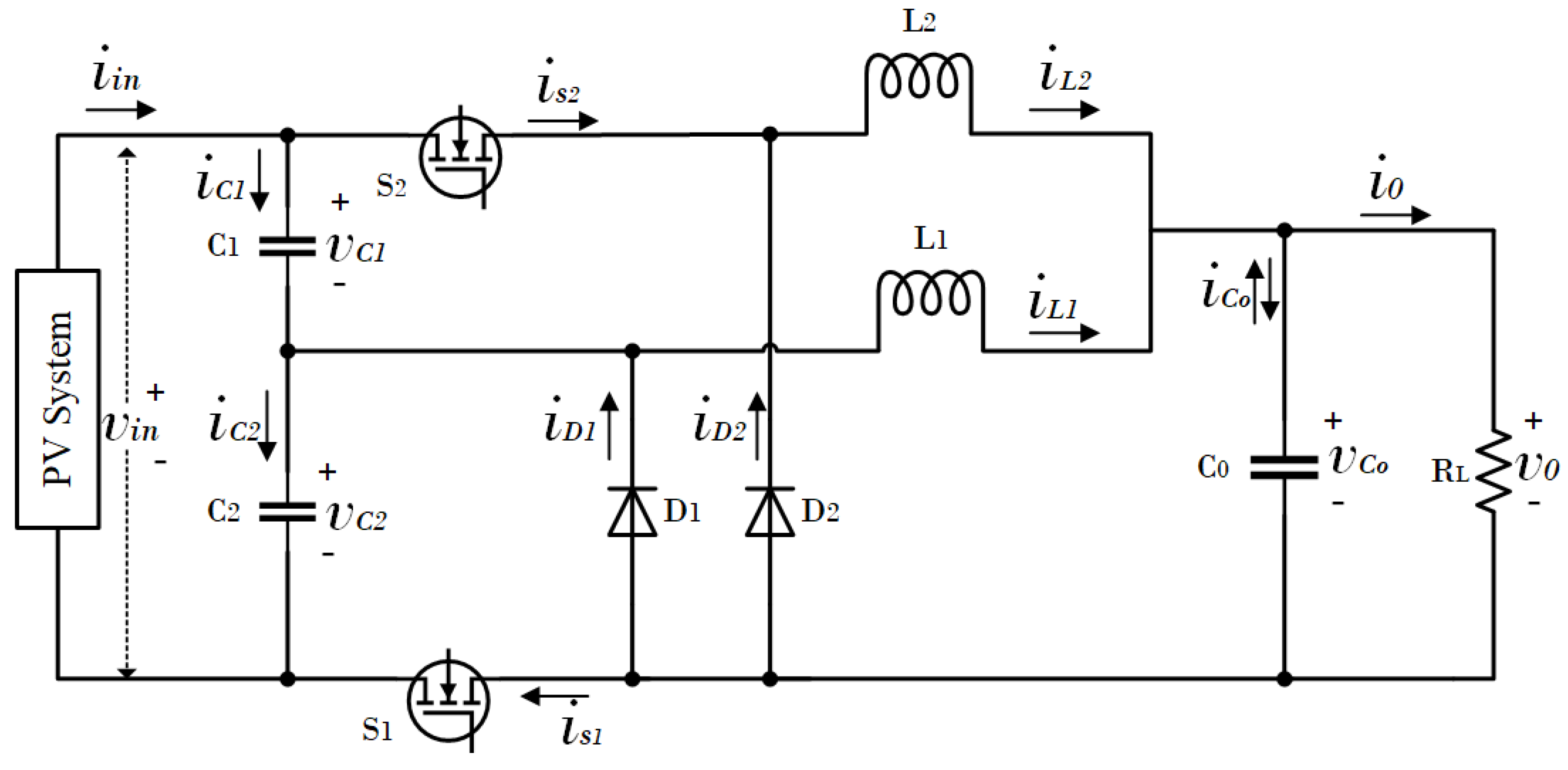
3. Modelling and Design of a Modified SC-HCR DC/DC Converter

The suggested converter is shown in Figure 2. When the switches are open, capacitors C1 and C2 are connected in series and parallel to the input voltage, resulting in Vc1 + Vc2 = Vin and Vc2 (Vin-Vc1). During the start-up phase, the capacitors are charged to their full capacity; thereafter, they are drained to keep the switch voltages constant. For the sake of simplicity, the capacitance values of C1 and C2 are assumed to be the same, and the voltage across each capacitor is the same. Vc1 = Vc2 = Vin/2. The enhanced converter’s operation was studied utilizing its four operating modes. The enhanced converter works in exactly the same way as the SC buck converter.

The inductor voltages were used to determine the voltage transfer gain for the proposed converter:

$$\left(0.5V_{in}-V_{out}\right)d{T}_s=V_{out}\left(1-d\right)T_s$$

(1)

$$V_{Tg}=\frac{V_{out}}{V_{in}}=\frac{d}{2}$$

(2)

The suggested converter’s output voltage was half of the input voltage. This indicates that the proposed converter converts at the highest possible level. This converter is mainly useful for high current and high-power systems.

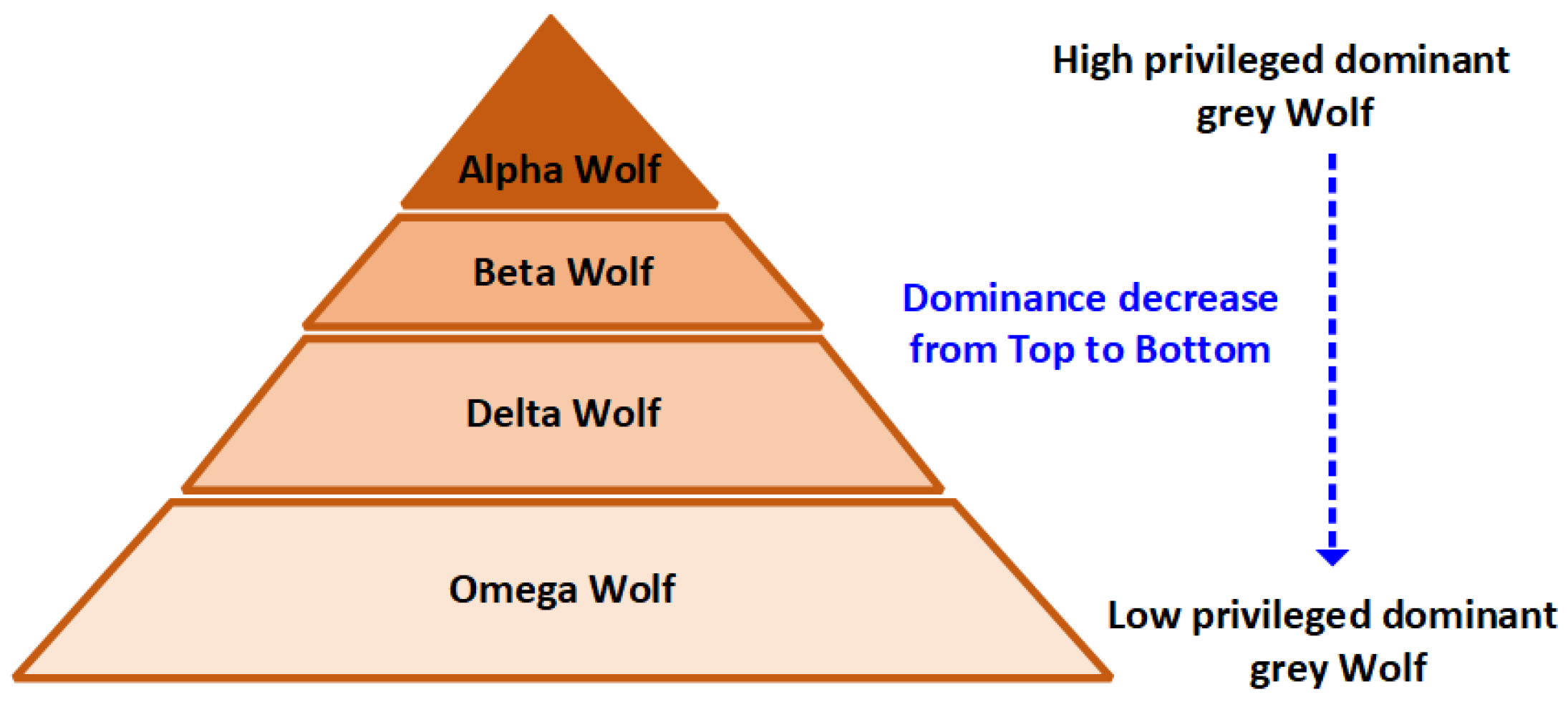
4. Grey Wolf Optimization Algorithm

Grey wolves are members of the Canidae family of animals. Grey wolves are the top predators in the food chain, making them apex predators. The usual group contains 6–12 wolves, with a social dominance structure. The alpha wolf is a dominant high-privileged grey wolf. The remaining wolves in the group must obey his or her commands. The whole pack honors the alpha by holding their tails low during meetings. This demonstrates that a pack’s structure and discipline are far more essential than their strength. The social order of wolves inspired the Grey Wolf Optimizer (GWO) algorithm [9,10]. Grey wolves engage in group hunting with hierarchy structure as shown in Figure 3.

Application of GWO Algorithm for Optimal Control Signal

Step 1: Parameter Initialization

In this step, the parameters of the controller, such as proportional gain ($K_p$) and integral gain ($K_i$) parameters, are initialised. Here, two gain parameters are involved, meaning grey wolves are searching for prey in two dimensions.

Step 2: Random Generation

The random behavior of gain parameters is generated based on the initialization of parameters.

Step 3: Objective Function

The fitness of the objective function is determined by the location of the prey. The objective function is expressed in terms of the error signal and is represented by the following equation:

$$\mathrm{u}=\min \left\{e\left(t\right)\right\}$$

(3)

where “u” is the objective function, “e(t)” error signal, “t” time period of signal.

Step 4: Following the prey

Following the prey, chasing it down, and approaching it.

Step 5: Encircling prey

Firstly, the grey wolves will encircle the victims, as previously stated.

Step 6: Hunting

Grey wolves can track down and encircle their victims during hunting. The hunt is often led by the alpha wolf. Those wolves have no idea where prey can be found in an undefined search area.

$$\overrightarrow{S_{\alpha }}=|\overrightarrow{R_1}·\overrightarrow{Y_{\alpha }}-\overrightarrow{Y}|; \overrightarrow{S_{\beta }}=|\overrightarrow{R_2}·\overrightarrow{Y_{\beta }}-\overrightarrow{Y}|; \overrightarrow{S_{\delta }}=|\overrightarrow{R_3}·\overrightarrow{Y_{\delta }}-\overrightarrow{Y}|;$$

(4)

$$\overrightarrow{Y_1}\left(t\right)=|\overrightarrow{Y_{\alpha }}-\overrightarrow{P_1}·\overrightarrow{S_{\alpha }}|; \overrightarrow{Y_2}\left(t\right)=|\overrightarrow{Y_{\beta }}-\overrightarrow{P_2}·\overrightarrow{S_{\beta }}|; \overrightarrow{Y_3}\left(t\right)=|\overrightarrow{Y_{\delta }}-\overrightarrow{P_3}·\overrightarrow{S_{\delta }}|;$$

(5)

Step 7: Upgraded position

After each individual’s fitness computation, the ideal solution is updated based on the value of the objective function.

$$\overrightarrow{Y}\left(i+1\right)=\frac{\overrightarrow{Y_1}\left(i\right)+\overrightarrow{Y_2}\left(i\right)+\overrightarrow{Y_3}\left(i\right)}{3}$$

(6)

$\overrightarrow{Y}\left(i\right)$ denotes the location vector of a grey wolf; ‘i’ denotes the current iteration.

Step 8: Obtain best fitness

The grey wolves reach prey by updating their positions according to the prey’s position, and at this point they have encircled the prey and finally hunted the prey. Similarly, the gain parameters adjust their value according to the error function value, finally obtaining the optimal function value.

5. System Outcomes and Its Analysis in MATLAB/Simulink Environment

Figure 4 shows the MATLAB/Simulink diagram of the proposed system associated with the GWO controller. This part evaluated the performance of the system under different scenarios with proposed and existing controllers.

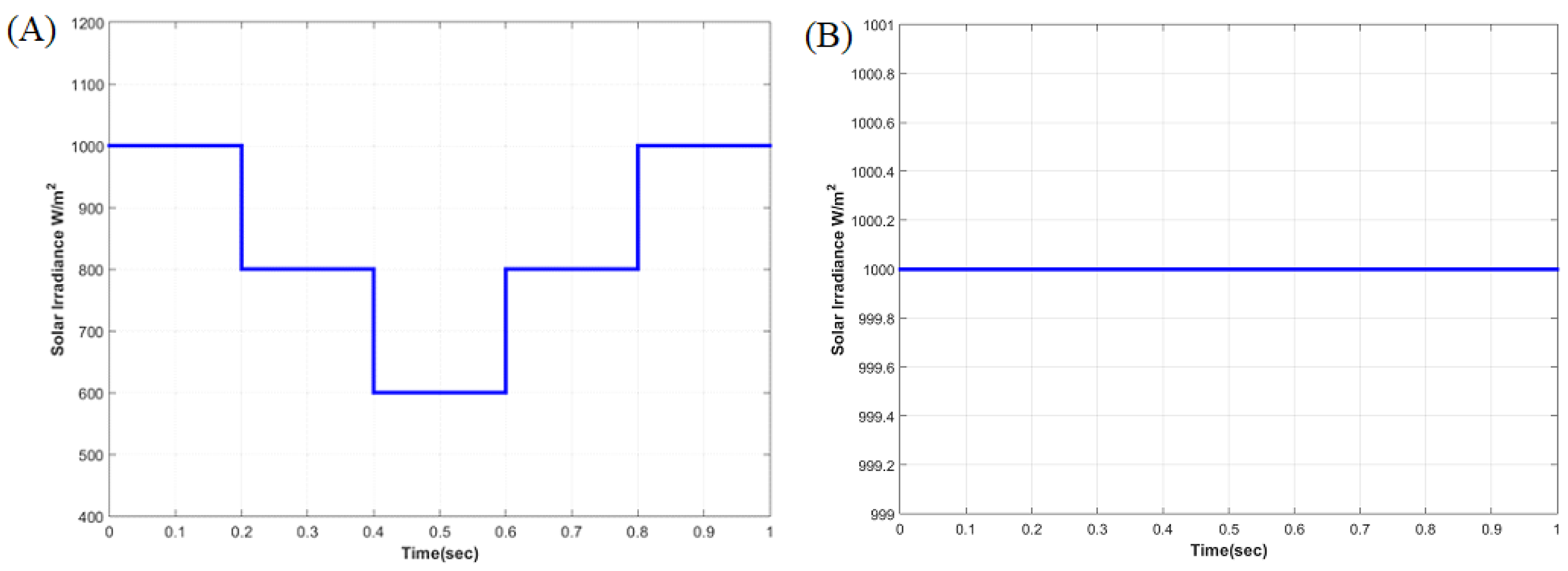
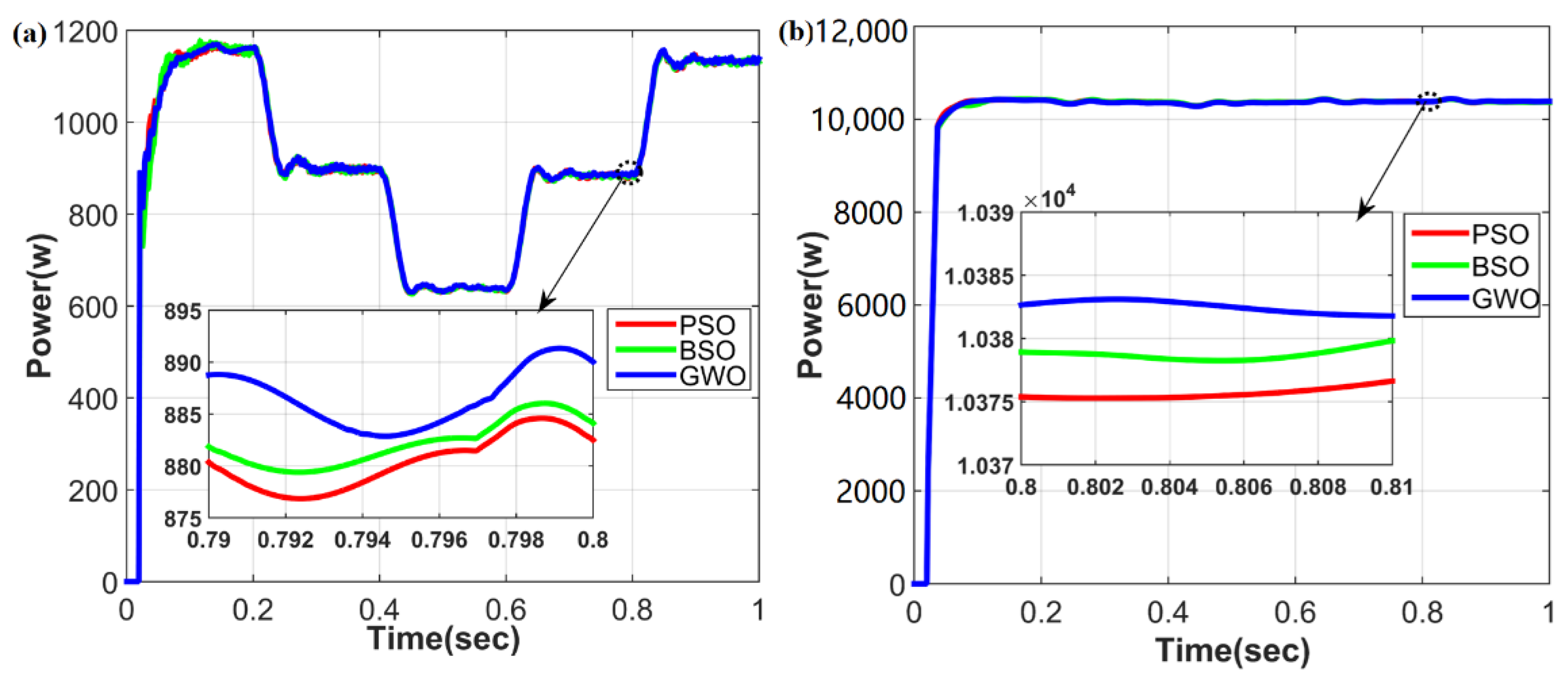
• Case 1: Changing of solar irradiance under constant Load

Case 1 is a grid-interfaced PV system with a suggested MSC-HCR converter and a chosen GWO controller, in terms of model outcomes. This was investigated when the solar irradiance varies while the load remains constant. Figure 5A shows that the $1000 \mathrm{W}/{\mathrm{m}}^2$ PV irradiance at time interval 0 was maintained for the following 0.2 s. After that, it falls linearly to $800 \mathrm{W}/{\mathrm{m}}^2$ in 0.2 s while maintaining the same amplitude up to 0.4 s. Following that, it drops linearly to $600 \mathrm{W}/{\mathrm{m}}^2$ at 0.4 s while maintaining the same amplitude until 0.6 s. Later, it grew to $800 \mathrm{W}/{\mathrm{m}}^2$ at 0.6 s and stayed the same for 0.8 s, ultimately rising to $1000 \mathrm{W}/{\mathrm{m}}^2$ at the same amplitude as before.

Under Case.1, subplot Figure 6a shows a comparison of PV converter power with existing and proposed methodologies. At 0.8 s, the system with the PSO technique produced a maximum output of 882 W. At 0.8 s, the system with the BSO technique achieved a maximum output of 884 W. At 0.8 s, the system using the suggested GWO approach produced a maximum output of 890 W. In this observation, the suggested converter’s output power was found to be high with the GWO technique. Figure 6b shows a comparison of load power with proposed and existing controllers. At 0.8 s, the system with the PSO technique achieved a maximum output of 10,375 W. At 0.8 s, the system using the BSO technique generated a maximum output of 10,378 W. At 0.8 s, the system using the suggested GWO approach achieved a maximum output of 10383 W. In comparison, the suggested method has high usable power. It was observed that the suggested GWO methodology had greater power availability at load and power usage in the system than other current methods.

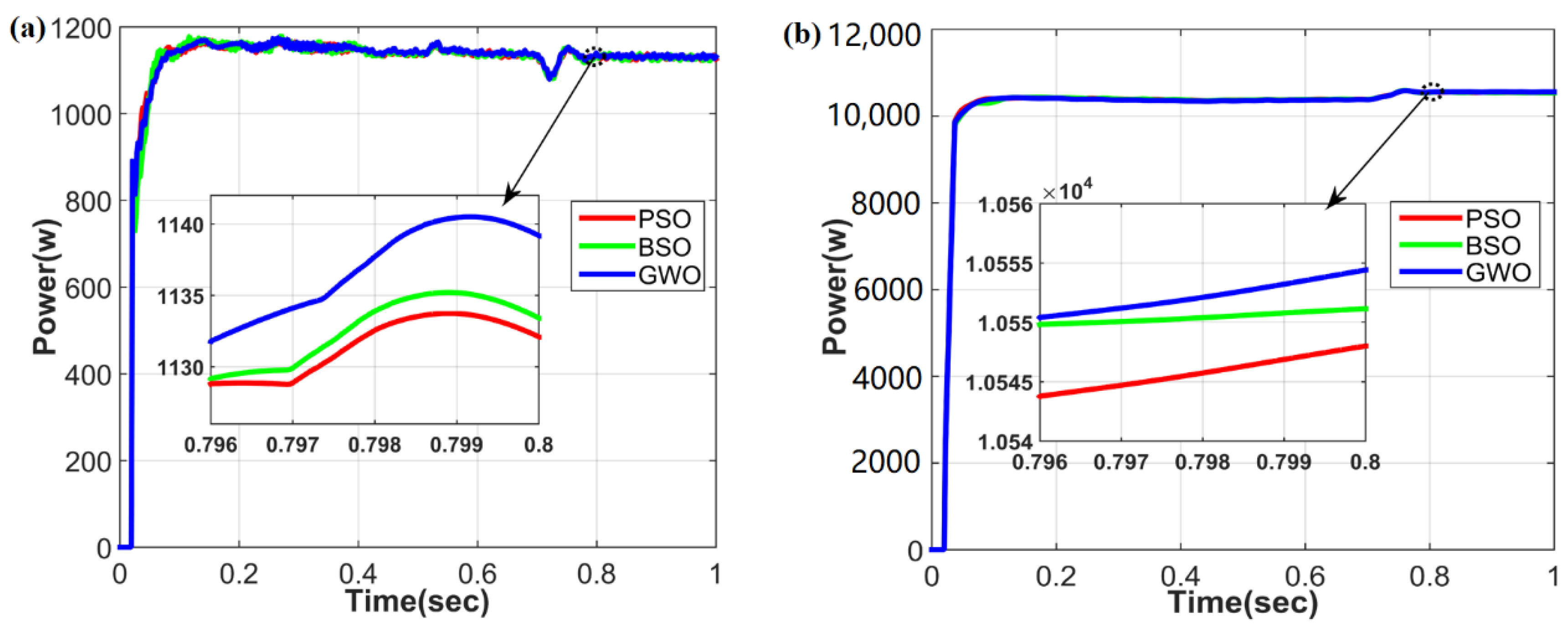
• Case 2: Changing Load under Steady PV irradiance

Case 2 is a grid-interfaced PV system with a suggested MSC-HCR converter and a chosen GWO controller, in terms of model outcomes. This was investigated under various loads at constant solar irradiance, which, as shown in Figure 5b, was investigated under various loads with steady PV irradiance. The constant irradiance ($1000 \mathrm{W}/{\mathrm{m}}^2$) was used at a temperature of 25 °C. The recommended GWO method was used to describe the system’s performance analysis.

Under case 2, subplot Figure 7a shows a comparison of PV converter power. At 0.8 s, the system with the PSO technique produced a maximum output of 1132 W. At 0.8 s, while the system with the BSO technique achieved a maximum output of 1134 W. At 0.8 s, the system using the suggested GWO approach produced a maximum output of 1140W. In this observation, the suggested converter’s output power was high with the GWO technique. Figure 7b shows a comparison of load power with proposed and existing controllers. At 0.8 s, the system with the PSO technique achieved a maximum output of 10,545 W. At 0.8 s, and the system using the BSO technique generated a maximum output of 10,550 W. At 0.8 s, the system using the suggested GWO approach achieved a maximum output of 10,555 W. In comparison to other current methodologies, the suggested method has high usable power. It was observed that the suggested GWO methodology has greater power availability at load.

6. Conclusions

This work used the innovative control method Grey Wolf Optimizer (GWO) to model and build a unique controller for a grid-interfaced PV system to achieve optimal power management in the system. A modified SC-HCR dc/dc converter was used in the system model, resulting in lower switching losses and higher converter efficiency. The system’s performance was investigated using the MATLAB/Simulink workbench. The performance of the suggested system was evaluated by comparing it to existing control techniques such as BSO and PSO. In terms of both accuracy and execution time, the GWO control strategy proved to be very competitive whereas the BSO control strategy was competitive but had a long execution time. The accuracy scores of the BSO control method were not excellent. This system model was tested in the following two scenarios: changing PV irradiance at constant load and constant PV irradiance at variable load. The proposed model’s simulation results show that the system’s efficiency improved. As a consequence, the suggested approach for power management is effective and efficient.