Adaptive Frequency and Assignment Algorithm for Context-Based Arithmetic Compression Codes for H.264 Video Intraframe Encoding †
Abstract
1. Introduction
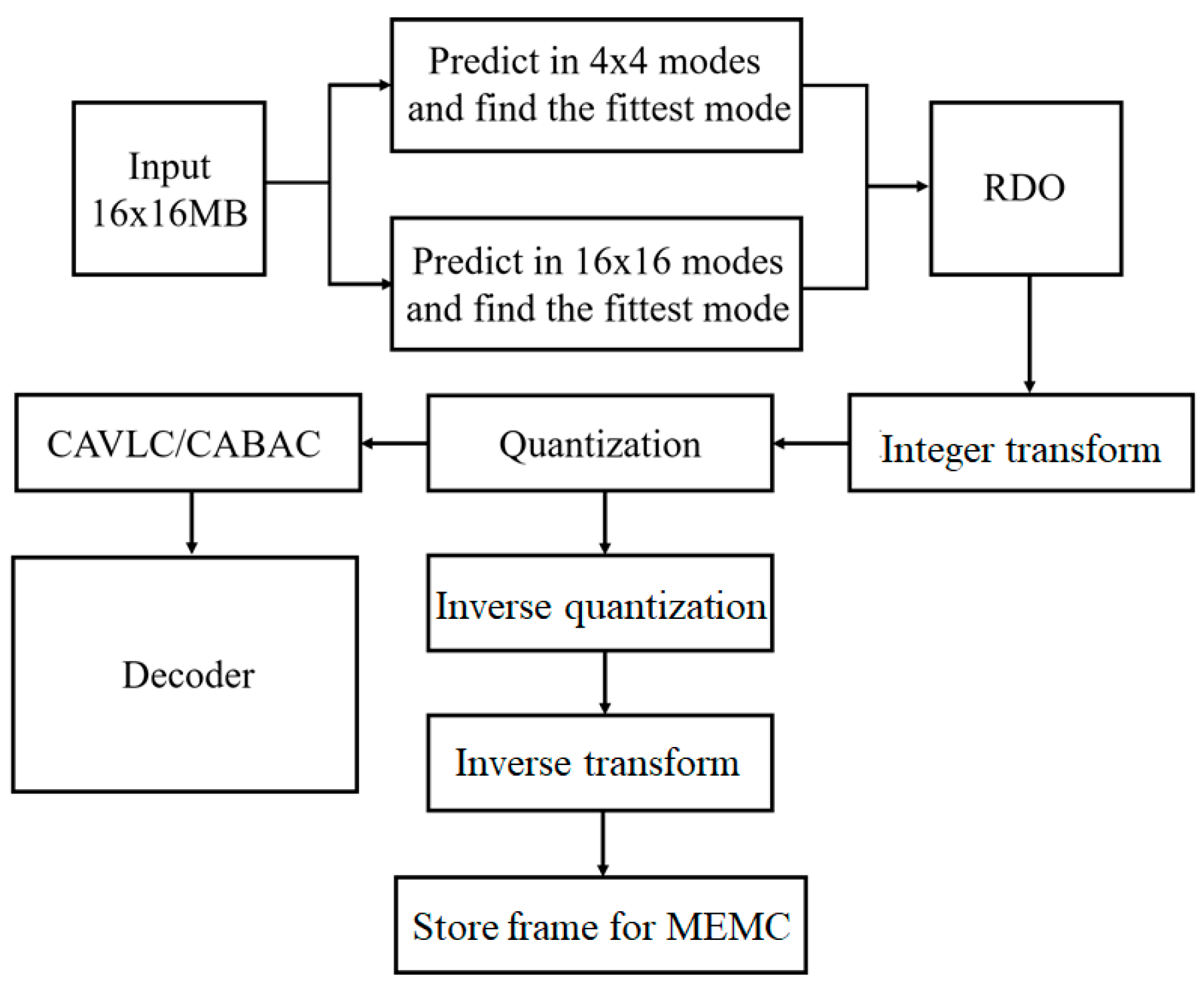
2. Proposed Intraframe Coding Scheme
2.1. Preprocessing
2.2. Context Modeling
2.3. AC Frequency Table
| Algorithm 1: Proposed adaptive frequency table squeezing method. |
| for idx=1:15 if idx==1 frequency_table(1:DC(i,j))*=W (Note: *= W means that the lefthanded side is multiplied by W) elseif idx==3 frequency_table(1:max(input(1:2)))*=X elseif idx==6 frequency_table(1: max(input(3:5)))*=Y elseif idx==10 frequency_table(1: max(input(6:9)))*=Z end |
2.4. Arithmetic Coding
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mansri, I.; Doghmane, N.; Kouadria, N.; Harize, S.; Bekhouch, A. Comparative evaluation of VVC, HEVC, H. 264, AV1, and VP9 encoders for low-delay video applications. In Proceedings of the 2020 Fourth International Conference on Multimedia Computing, Networking and Applications (MCNA), Valencia, Spain, 19–22 October 2020; pp. 38–43. [Google Scholar]
- Sullivan, G.J.; Wiegand, T. Video compression: From concepts to the H.264/AVC standard. Proc. IEEE 2005, 93, 18–31. [Google Scholar] [CrossRef]
- Wiegand, T.; Sullivan, G.J.; Bjontegaard, G.; Luthra, A. Overview of the H.264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 560–576. [Google Scholar] [CrossRef]
- Luthra, A.; Sullivan, G.J.; Wiegand, T. Introduction to the special issue on the H.264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 557–559. [Google Scholar] [CrossRef]
- Pastuszak, G.; Abramowski, A. Algorithm and architecture design of the H. 265/HEVC intra encoder. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 210–222. [Google Scholar] [CrossRef]
- Lainema, J.; Bossen, F.; Han, W.J.; Min, J.; Ugur, K. Intra coding of the HEVC standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1792–1801. [Google Scholar] [CrossRef]
- Sullivan, G.J.; Ohm, J.R.; Han, W.J.; Wiegand, T. Overview of the high efficiency video coding (HEVC) standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1649–1668. [Google Scholar] [CrossRef]
- Saldanha, M.; Corrêa, M.; Corrêa, G.; Palomino, D.; Porto, M.; Zatt, B.; Agostini, L. An overview of dedicated hardware designs for state-of-the-art AV1 and H.266/VVC video codecs. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar]
- Mukherjee, D.; Bankoski, J.; Grange, A.; Han, J.; Koleszar, J.; Wilkins, P.; Xu, Y.; Bultje, R. The latest open-source video codec VP9—An overview and preliminary results. In Proceedings of the 2013 Picture Coding Symposium (PCS), San Jose, CA, USA, 8–11 December 2013; pp. 390–393. [Google Scholar]
- Chen, Y.; Murherjee, D.; Han, J.; Grange, A.; Xu, Y.; Liu, Z.; Parker, S.; Chen, C.; Su, H.; Joshi, U.; et al. An overview of core coding tools in the AV1 video codec. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 41–45. [Google Scholar]
- Viitanen, M.; Sainio, J.; Mercat, A.; Lemmetti, A.; Vanne, J. From HEVC to VVC: The first development steps of a practical intra video encoder. IEEE Trans. Consum. Electron. 2022, 68, 139–148. [Google Scholar] [CrossRef]
- Bross, B.; Chen, J.; Ohm, J.R.; Sullivan, G.J.; Wang, Y.K. Developments in international video coding standardization after AVC, with an overview of versatile video coding (VVC). Proc. IEEE 2021, 109, 1463–1493. [Google Scholar] [CrossRef]
- Grange, A.; de Rivaz, P.; Hunt, J. VP9 Bitstream & Decoding Process Specification. Available online: https://storage.googleapis.com/downloads.webmproject.org/docs/vp9/vp9-bitstream-specification-v0.6-20160331-draft.pdf (accessed on 29 February 2024).
- Sullivan, G.J.; Wiegand, T. Rate-distortion optimization for video compression. IEEE Signal Process. Mag. 1998, 15, 74–90. [Google Scholar] [CrossRef]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE Trans. Comput. 1974, 23, 90–93. [Google Scholar] [CrossRef]
- Malvar, H.S.; Hallapuro, A.; Karczewicz, M.; Kerofsky, L. Low-complexity transform and quantization in H.264/AVC. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 598–603. [Google Scholar] [CrossRef]
- Ghasempour, M.; Ghanbari, M. A low complexity system for multiple data embedding into H.264 coded video bit-stream. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4009–4019. [Google Scholar] [CrossRef]
- Wallace, G.K. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, 18–34. [Google Scholar] [CrossRef]
- Ding, J.J.; Wang, I.H.; Chen, H.Y. Improved efficiency on adaptive arithmetic coding for data compression using range-adjusting scheme, increasingly adjusting step, and mutual-learning scheme. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 3412–3423. [Google Scholar] [CrossRef]
- Internet Archive. 2023. Available online: https://web.archive.org/web/20230509144046/http://trace.eas.asu.edu/yuv/index.html (accessed on 29 February 2024).
- 1920x1080.yuv Images for AVC Codec. 2017. Available online: https://github.com/ireader/avcodec/blob/master/libavo/test/1920x1080.yuv (accessed on 29 February 2024).
- Index of Video. 2010. Available online: https://media.xiph.org/video (accessed on 29 February 2024).
- Richardson, I.E.G. H. 264 and MPEG-4 Video Compression: Video Coding for Next-Generation Multimedia; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]


| Current Suffix Length | Threshold for Increasing Suffix Length |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
| 3 | 12 |
| 4 | 24 |
| 5 | 48 |
| 6 | N/A (highest) |
| Level | Suffix Length = 0 | Level | Suffix Length = 1 |
|---|---|---|---|
| 1 | 1 | 1 | 10 |
| −1 | 01 | −1 | 11 |
| 2 | 001 | 2 | 010 |
| −2 | 0001 | −2 | 011 |
| 3 | 00001 | 3 | 010 |
| −3 | 000001 | −3 | 0011 |
| … | … | … | … |
| −7 | 00000000000001 | 14 | 000000000000010 |
| 000000000000001xxxx | −14 | 000000000000011 | |
| 0000000000000001xxxxxxxxxxxx | 15 | 0000000000000010 | |
| −15 | 0000000000000011 | ||
| 0000000000000001xxxxxxxxxxxx | |||
| X | 6 | 4 | 1 |
| 4 | 4 | 3 | 2 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| X | 2 | 3 | 9 |
| 1 | 4 | 8 | 10 |
| 5 | 7 | 11 | 14 |
| 6 | 12 | 13 | 15 |
| Input | CAVLC | Proposed | Reduction |
|---|---|---|---|
| Akiyo | 177,925 | 171,230 | −3.18% |
| bridge-close | 370,383 | 331,572 | −10.48% |
| bridge-far | 301,698 | 257,717 | −14.58% |
| bus | 399,413 | 362,545 | −9.23% |
| foreman | 275,447 | 251,234 | −8.79% |
| flower | 359,706 | 326,845 | −9.14% |
| mother | 187,798 | 181,465 | −3.37% |
| news | 232,595 | 222,265 | −4.44% |
| silent | 342,727 | 302,813 | −11.64% |
| waterfall | 400,367 | 356,244 | −11.02% |
| Average bit reduction | −8.58% | ||
| Input | CAVLC | Proposed | Reduction |
|---|---|---|---|
| Akiyo | 52,938 | 51,761 | −2.22% |
| bridge-close | 103,432 | 91,247 | −11.78% |
| bridge-far | 77,659 | 67,597 | −12.96% |
| foreman | 79,643 | 73,088 | −8.23% |
| mother | 59,212 | 56,002 | −5.42% |
| news | 72,418 | 69,272 | −4.34% |
| silent | 88,899 | 80,225 | −9.76% |
| Average bit reduction | −7.81% | ||
| Input | CAVLC | Proposed | Reduction |
|---|---|---|---|
| AOV5 | 4,711,101 | 4,405,510 | −6.49% |
| Time lapse | 3,030,756 | 2,882,682 | −4.89% |
| camera1 | 2,979,962 | 2,772,831 | −6.95% |
| west wind | 3,353,710 | 3,270,767 | −2.47% |
| rush fields | 5,436,880 | 5,000,844 | −8.02% |
| controlled burn | 6,905,301 | 6,314,721 | −8.55% |
| life | 5,374,526 | 4,741,603 | −11.78% |
| pedestrian | 3,422,777 | 3,089,042 | −9.75% |
| park joy | 6,513,638 | 5,729,934 | −12.03% |
| Average bit reduction | −7.88% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, H.-C.; Ding, J.-J. Adaptive Frequency and Assignment Algorithm for Context-Based Arithmetic Compression Codes for H.264 Video Intraframe Encoding. Eng. Proc. 2025, 98, 4. https://doi.org/10.3390/engproc2025098004
Hsu H-C, Ding J-J. Adaptive Frequency and Assignment Algorithm for Context-Based Arithmetic Compression Codes for H.264 Video Intraframe Encoding. Engineering Proceedings. 2025; 98(1):4. https://doi.org/10.3390/engproc2025098004
Chicago/Turabian StyleHsu, Huang-Chun, and Jian-Jiun Ding. 2025. "Adaptive Frequency and Assignment Algorithm for Context-Based Arithmetic Compression Codes for H.264 Video Intraframe Encoding" Engineering Proceedings 98, no. 1: 4. https://doi.org/10.3390/engproc2025098004
APA StyleHsu, H.-C., & Ding, J.-J. (2025). Adaptive Frequency and Assignment Algorithm for Context-Based Arithmetic Compression Codes for H.264 Video Intraframe Encoding. Engineering Proceedings, 98(1), 4. https://doi.org/10.3390/engproc2025098004







