Primitive Shape Fitting of Stone Projectiles in Siege Weapons: Geometric Analysis of Roman Artillery Ammunition †
Abstract
1. Introduction
2. Materials and Methods
2.1. The Case Study
2.2. Three-Dimensional Documentation
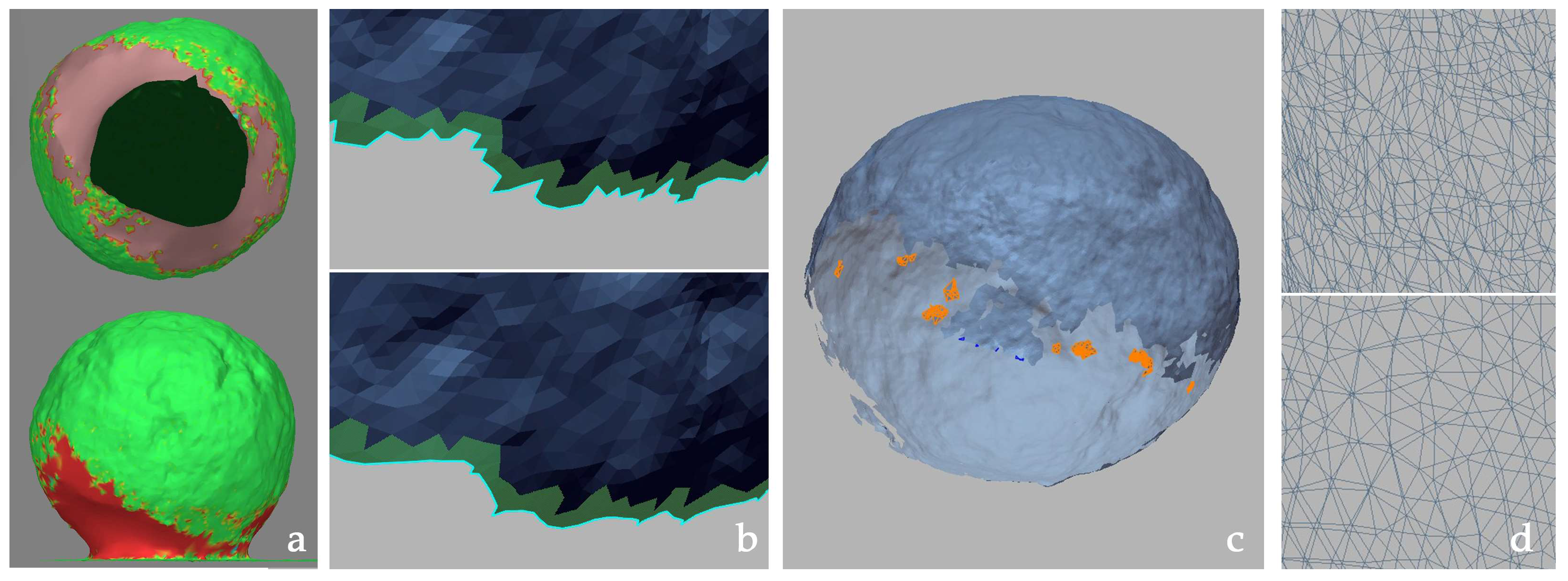
- Initial mesh editing: The lower, less documented, and more uncertain part was removed by trimming the edges to eliminate unreliable polygonal surfaces. Most image processing software also includes built-in tools for filtering and assessing model confidence (a). Irrelevant parts could be manually removed, especially because the objects were stacked, leading to unintended geometry reconstructions. The boundary editing tool extended the selection to refine edge regions affected by poor lighting or contact with other objects. Finally, an edge smoothing process was applied to improve surface continuity (b).
- Surface refinement: Smoothing operations helped to eliminate inconsistencies caused by the presence of moss, lichen, or non-removable weed vegetation.
- Mesh cleaning: Small hole-filling operations (within a certain size) and automatic corrections (e.g., removal of self-intersecting faces, minor and pendant faces, and clusters) improved the model’s accuracy (c);
- Mesh optimization: Additional refinements were applied to regularize the mesh structure (d).
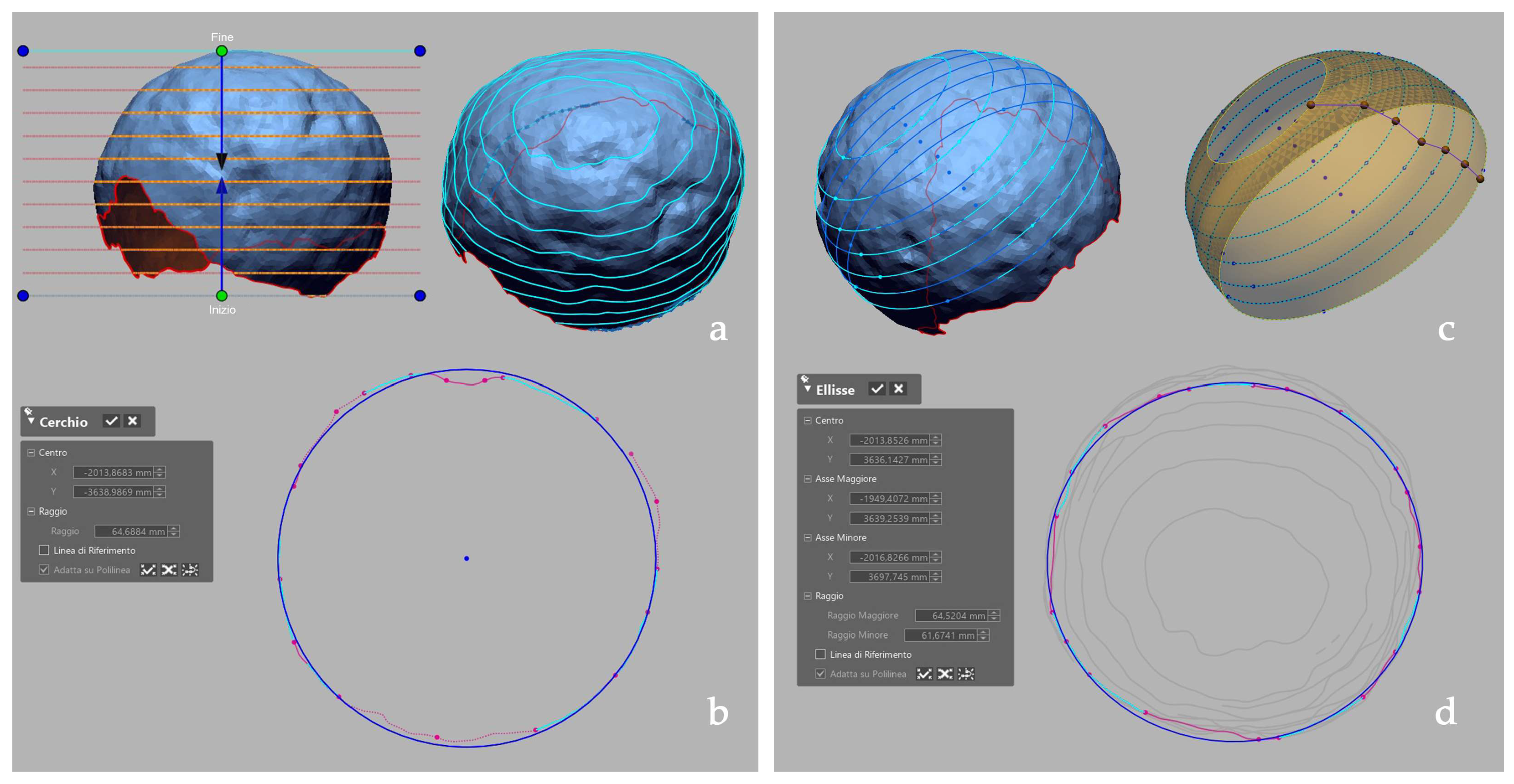
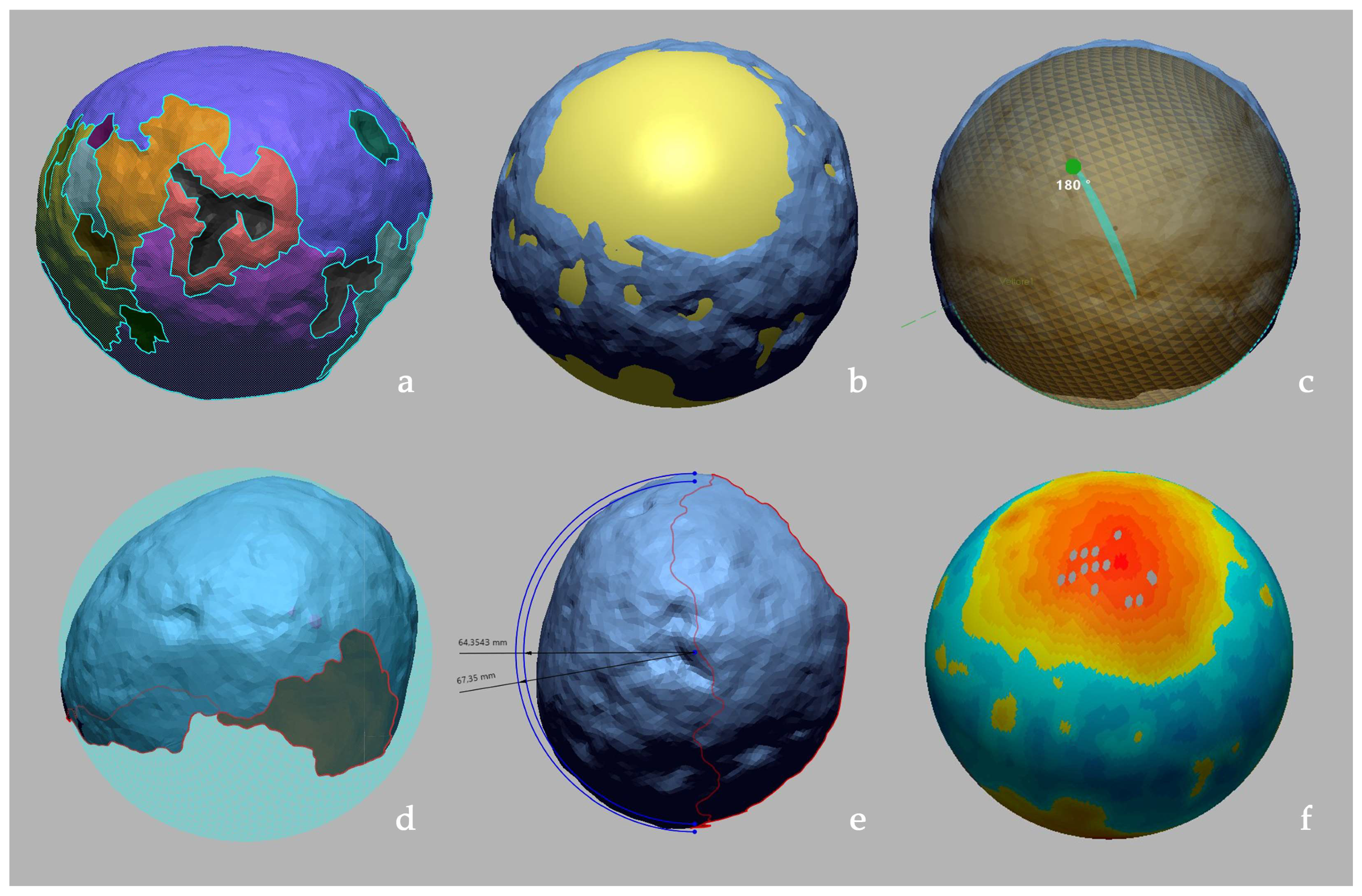
3. Results
4. Discussion and Future Developments
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-Dimensional |
| ASE | Automatic Surface Extraction |
| CH | Cultural Heritage |
| B-F | Best-fitting |
| LSEF | Least Squares Ellipsoid Fitting |
| MSR | Manual Surface Reconstruction |
| SfM | Structure from Motion |
References
- Fico, D.; Rizzo, D. (Eds.) Conservation Methodologies and Practices for Built Heritage; MDPI—Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2025; ISBN 978-3-7258-2743-5. [Google Scholar]
- Guarnieri, A.; Vettore, A.; El-Hakim, S.; Gonzo, L. Digital Photogrammetry and Laser Scanning in Cultural Heritage Survey. In Proceedings of the ISPRS XX Symposium, Istanbul, Turkey, 15 June 2004; Volume 2, pp. 1–6. [Google Scholar]
- Fassi, F.; Achille, C.; Fregonese, L.; Monti, C. Multiple Data Source for Survey and Modelling of Very Complex Architecture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, XXXVIII, 234–239. [Google Scholar]
- Fascia, R.; Barbieri, F.; Gaspari, F.; Ioli, F.; Pinto, L. From 3D Survey to Digital Reality of a Complex Architecture: A Digital Workflow for Cultural Heritage Promotion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-2-W4-2024, 205–212. [Google Scholar] [CrossRef]
- Astorga González, E.M.; Municio, E.; Noriega Alemán, M.; Marquez-Barja, J.M. Cultural Heritage and Internet of Things. In GoodTechs ’20: Proceedings of the 6th EAI International Conference on Smart Objects and Technologies for Social Good, Antwerp, Belgium, 14–16 September 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 248–251. [Google Scholar] [CrossRef]
- Casillo, M.; Colace, F.; Gaeta, R.; Lorusso, A.; Santaniello, D.; Valentino, C. Revolutionizing Cultural Heritage Preservation: An Innovative IoT-Based Framework for Protecting Historical Buildings. Evol. Intell. 2024, 17, 3815–3831. [Google Scholar] [CrossRef]
- Costantino, C.; Prati, D.; Predari, G.; Bartolomei, C. 3D Laser Scanning Survey for Cultural Heritage. A Flexible Methodology to Optimize Data Collection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 821–828. [Google Scholar] [CrossRef]
- Li, F.; Spettu, F.; Achille, C.; Vassena, G.; Fassi, F. The Role of Web Platforms in Balancing Sustainable Conservation and Development in Large Archaeological Site: The Naxos Case Study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-2-W8-2024, 303–310. [Google Scholar] [CrossRef]
- Spiess, F.; Waltenspül, R.; Schuldt, H. The Sketchfab 3D Creative Commons Collection (S3D3C). arXiv 2024, arXiv:2407.17205. [Google Scholar] [CrossRef]
- Bertacchi, S.; Juan Vidal, F.; Fantini, F. Ancient Architectural Design Interpretation: A Framework Based on Alexandrian Manuals. Acta IMEKO 2024, 13, 1–9. [Google Scholar] [CrossRef]
- Adembri, B.; Cipriani, L.; Bertacchi, G. Guidelines for a Digital Reinterpretation of Architectural Restoration Work: Reality-Based Models and Reverse Modelling Techniques Applied to the Architectural Decoration of the Teatro Marittimo, Villa Adriana. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-5/W1, 599–606. [Google Scholar] [CrossRef]
- Eramo, E.; Cinque, G.E. The Vault of the So-Called Serapeum: An Ellipsoidal Geometry at Hadrian’s Villa. In Graphic Horizons; Hermida González, L., Xavier, J.P., Pernas Alonso, I., Losada Pérez, C., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 51–58. [Google Scholar] [CrossRef]
- Rossi, A. The Survey of the Ballistic Imprints for a Renewed Image of Unearthed Pompeii. Nexus Netw. J. 2024, 26, 307–324. [Google Scholar] [CrossRef]
- Bertacchi, S.; Gonizzi Barsanti, S.; Rossi, A. Geometry of Wall Degradation: Measuring and Visualising Impact Craters in the Northern Walls of Pompeii. SCIRES-IT-Sci. Res. Inf. Technol. 2024, 14, 111–128. [Google Scholar] [CrossRef]
- Russo, F.; Russo, F. 89 a.C. Assedio a Pompei: La Dinamica e Le Tecnologie Belliche Della Conquista Sillana Di Pompei; Edizioni Flavius: Pompei, Italy, 2005; ISBN 88-88419-32-2. [Google Scholar]
- Vitruvius, P. De Architectura; Gros, P., Ed.; Einaudi: Torino, Italy, 1997. [Google Scholar]
- Holley, A.E. The Ballista Balls from Masada. In Masada IV: The Yigael Yadin Excavations 1963–1965. Final Reports; Aviram, J., Foerster, G., Netzer, E., Eds.; Israel Exploration Society: Hebrew University of Jerusalem: Jerusalem, Israel, 1994; pp. 347–365. ISBN 978-965-221-010-4. [Google Scholar]
- Wilkins, A.; Barnard, H.; Rose, P.J. Roman Artillery Balls from Qasr Ibrim, Egypt. Sudan Nubia Sudan Archaeol. Res. Soc. 2006, 10, 64–78. [Google Scholar]
- Wilkins, A. Roman Imperial Artillery: Outranging the Enemies of the Empire, 3rd ed.; Archaeopress Roman Archaeology; Archaeopress: Oxford, UK, 2024; ISBN 978-1-80327-783-7. [Google Scholar]
- Maiuri, A. Studi e Ricerche Sulla Fortificazione di Pompei; Monumenti Antichi Pubblicati per cura della R. Accademia dei Lincei; Hoepli: Milano, Italy, 1929; Volume 33. [Google Scholar]
- Giglio, M.; Pesando, F. La Guerra sociale, l’assedio e la fine di Pompei sannitica. In Proceedings of the Pompei 79 d.C. Una Storia Romana, Roma, Italy, 6 November 2020–31 January 2021; Torelli, M., Ed.; Electa: Milano, Italy, 2020; pp. 144–151, ISBN 978-88-9282-011-1. [Google Scholar]
- Di Marco, U.; Molari, P.G. Archimede ed il sistema di caricamento della balista da un talento utilizzata nella fortezza dell’Eurialo di Siracusa. In Proceedings of the 4th International Conference|Atti dell’8° Convegno Nazionale, Naples, Italy, 11 December 2020; D’Agostino, S., d’Ambrosio Alfano, F.R., Eds.; Cuzzolin: Napoli, Italy, 2020; Volume I, pp. 393–408. [Google Scholar]
- Van Buren, A.W. Further Pompeian Studies. MAAR 1932, 10, 7–54. [Google Scholar] [CrossRef]
- Piranesi, F.; Guattani, G.A. Antiquités de la Grande Grèce, Aujourd’hui Royaume de Naples, Gravées par François Piranesi; Piranesi Leblanc: Paris, France, 1804; Volume 1. [Google Scholar]
- Van Buren, A.W. Further Studies in Pompeian Archaeology. MAAR 1925, 5, 103–113. [Google Scholar] [CrossRef]
- Fiorelli, G. Pompeianarum Antiquitatum Historia; s.n.: Napoli, Italy, 1862; Volume 2. [Google Scholar]
- Fiorelli, G. Gli Scavi di Pompei dal 1861 al 1872 Relazione al Ministro della Istruzione Pubblica di Giuseppe Fiorelli; Tipografia italiana nel liceo V. Emanuele: Napoli, Italy, 1873. [Google Scholar]
- Schumacher, G. Tell El Mutesellim. Bericht Über Die 1903 Bis 1905 Mit Unterstützung SR. Majestät Des Deutschen Kaisers Und Der Deutschen Orientgesellschaft Vom Deutschen Verein Zur Erforschung Palästinas Veranstalteten Ausgrabungen; Rudolf Haupt: Leipzig, Germany, 1908. [Google Scholar]
- Burns, M. Pompeii under Siege: A Missile Assemblage from the Social War. JRMES 2015, 14/15, 1–10. [Google Scholar]
- Agisoft Metashape Professional. Available online: https://www.agisoft.com/ (accessed on 1 February 2025).
- 3D Systems Geomagic Design X. Available online: https://www.3dsystems.com/software/geomagic-design-x (accessed on 1 February 2025).
- Maiuri, A. Pompei. Isolamento della cinta murale tra la Porta Vesuvio e la Porta Ercolano. Not. Degli Scavi Antich. 1943, VII, 275–314. [Google Scholar]
- Tesema, K.W.; Hill, L.; Jones, M.W.; Ahmad, M.I.; Tam, G.K.L. Point Cloud Completion: A Survey. IEEE Trans. Vis. Comput. Graph. 2024, 30, 6880–6899. [Google Scholar] [CrossRef] [PubMed]
- Diao, H.; Jiang, X.; Fan, Y.; Li, M.; Wu, H. 3D Face Reconstruction Based on a Single Image: A Review. IEEE Access 2024, 12, 59450–59473. [Google Scholar] [CrossRef]
- Eramo, E.; Fantini, F. An Integrated Approach for Investigating Roman Cupolas: From Segmented Models to Trikentron Analyis. Disegnarecon 2024, 17, 5.1–5.12. [Google Scholar] [CrossRef]
- Li, Q.; Griffiths, J.G. Least Squares Ellipsoid Specific Fitting. In Proceedings of the Geometric Modeling and Processing 2004 (GMP’04), Beijing, China, 13–15 April 2004; pp. 335–340. [Google Scholar] [CrossRef]
- Python. Available online: https://www.python.org (accessed on 23 March 2025).
- Rhinoceros (Rhino 3D). Available online: https://www.rhino3d.com (accessed on 1 February 2025).
- Grasshopper. Algorithmic Modeling for Rhino. Available online: https://www.grasshopper3d.com (accessed on 23 March 2025).
- ChatGPT (OpenAI). Available online: https://openai.com/chatgpt (accessed on 2 April 2025).
- Molari, P.G.; Maraldi, M.; Angelini, G.; Bignami, S.; Lionello, G. La ricostruzione della balista di Vitruvio. In Proceedings of the Quinta Giornata di Studio Ettore Funaioli (V GEF), Bologna, Italy, 15 July 2011; 2012; pp. 1–26. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertacchi, S. Primitive Shape Fitting of Stone Projectiles in Siege Weapons: Geometric Analysis of Roman Artillery Ammunition. Eng. Proc. 2025, 96, 3. https://doi.org/10.3390/engproc2025096003
Bertacchi S. Primitive Shape Fitting of Stone Projectiles in Siege Weapons: Geometric Analysis of Roman Artillery Ammunition. Engineering Proceedings. 2025; 96(1):3. https://doi.org/10.3390/engproc2025096003
Chicago/Turabian StyleBertacchi, Silvia. 2025. "Primitive Shape Fitting of Stone Projectiles in Siege Weapons: Geometric Analysis of Roman Artillery Ammunition" Engineering Proceedings 96, no. 1: 3. https://doi.org/10.3390/engproc2025096003
APA StyleBertacchi, S. (2025). Primitive Shape Fitting of Stone Projectiles in Siege Weapons: Geometric Analysis of Roman Artillery Ammunition. Engineering Proceedings, 96(1), 3. https://doi.org/10.3390/engproc2025096003




