The Hub Location Problem in Air Transportation: A Review ^†

Abstract

The hub location problem is constantly examined in the field of air transportation, especially when designing networks for passenger airlines or express cargo providers. The competition that characterizes these businesses combined with the small benefit margins of the industry puts more pressure on finding innovative optimization tools when designing networks, locating hubs, and opening new routes with the minimum cost, usually under strict capacity constraints. This review covers the hub location problem in air transportation and its different mathematical models in preparation for a detailed SLR.

1. Introduction

Air transportation is a very competitive business due to the high offer per demand ratio. This makes it hard for airlines to specifically optimize their profit margins, since the main revenue streams of airlines come from passengers’ fees or cargo revenues. Airports and governmental civil aviation authorities gain their business revenues from different streams not directly oriented to the final customer (either passenger or freight). In facthas stated that “Although the recovery (From the pandemic effects) is impressive, a net benefit margin of 2.7% (The global average of air transportation business) is way inferior to what investors in any other sector would accept”.

Nonetheless, the constant growth of global traffic indicates that airlines and related business providers can continue optimizing their network to further benefit from this growth. Indeed, shows that global traffic continued to show strong resilience by March 2024, at 18.9% YoY in terms of RPK (Revenue Passenger Kilometers), maintaining pre-pandemic industry trends. Consequently, it is always very important for both airlines and airports to carefully choose the network design strategy that responds the best to the economic parameters involved.

The hub location problem is at the center of network design for airlines, airports, and countries in general. Indeed, theoretical studies suggest that implementing economies of scale in a hub-and-spoke network can lead to better fares and costs than in a classic point-to-point network [1]. Consequently, it is important to review the different mathematical models in the literature. Two allocation problems regarding the assignment of demand sources to hub nodes have been studied in the literature: single-allocation problems and multiple-allocation problems [2]. Moreover, the connection between hubs and centers determines the type of hub-and-spoke network: 1—pure hub-and-spoke network; 2—hub-and-spoke with pick-up stopovers and feeders; and 3—hub-and-spoke with center-to-center directs [3].

It is important to mention that in a competitive environment like the air transportation market, the hub location problem would ideally be examined through different competition frameworks and using diverse models, such as game theory, to seek equilibria [4].

The objective of this paper is to examine the existing literature on the hub location problem in the air transportation business that addresses modeling and mathematical approaches. The scope encompasses studies on both continuous and discrete models, starting from the first paper that considered the hub location problem as a quadratic integer program [5] in 1987. Finally, this review will try to emphasize different location factors such as the economic impact, geographic impact, and competition element. Consequently, by focusing only on the air transportation field, this review demonstrates the continuous need for more studies on this subject as the airline business continues handling complex network design situations adapted to real-life conditions.

The remainder of this paper is composed of three sections: Section 2 discusses the methodology adopted to produce this review. Section 3 has two subsections, presenting a descriptive analysis of the results followed by an examination of the hub location factors and their models in the air transportation literature. Finally, Section 4 summarizes the conclusions of this work.

2. Materials and Methods

The aim of this study is to explore how the hub location problem has been examined, analyzed, and used in the supply chain field, with a specific focus on the air transportation process. We provide a state-of-the-art review of the literature handling the target problem. Indeed, this review will serve as a basis for a larger systematic literature review on the matter.

This literature review aims to set a foundation upon which new knowledge can be obtained, starting from empirical findings explored and used from different perspectives [6].

This review focused on a keyword search of two databases: Google scholar and Scopus. The search strings used combined predefined keywords as follows:

• “hub location problem*” and “supply chain management”;
• “hub location problem*” and “SCM”;
• “Hub location problem*” and “logistics”;
• “Hub location problem*” and “air logistics”;
• “hub location problem*” AND “air transport*”;
• “hub location problem*” AND “Hub and spoke network” AND “model*”;
• “Hub location problem*” and “model*” and “air transport*”;
• “Hub location problem*” AND “Hub and spoke network” and “model*” and “air transport*”;
• “Hub location problem*” OR “Hub and spoke network” AND “model*” AND “air transport*.

The search was carried out between 5 October and 1 November 2024 using the keywords and search strings above in sequence, yielding the following results:

• Google Scholar generated a high number of articles (565).
• Scopus only generated 15 articles.

Thus, the following inclusion and exclusion criteria were applied to reduce the relevant articles from Google Scholar to those on the state of the art:

• Only papers in English were taken into consideration;
• Any article whose subject or abstract did not mention air transportation or the airline industry (or an equivalent) was not taken into consideration;
• Only articles from 2000 to 2024 were taken into consideration;
• Articles that mention air transportation in the abstract but whose content is related to railway, maritime, or roadway transportation were excluded.

The inclusion and exclusion criteria used for the 15 articles found in Scopus were the following:

• Only papers in English were taken into consideration;
• Any paper whose content was not directly related to the hub location problem, its models, or “airline or air transportation” was not taken into consideration, for example, “air taxi, Skyport location problem… for airport access”.

The application of the inclusion and exclusion criteria on the initial results (565 articles from Google Scholar and 15 articles from Scopus) reduced the papers from Scopus to 11 and those from Google Scholar to 19 after also eliminating the replicates between the two databases. Thus, a total of 30 papers were obtained within the scope of our study.

3. Results and Discussion

3.1. Descriptive Analysis

3.1.1. History of Publications

Per the inclusion and exclusion criteria, the lower range for the publication date of the papers examined from Google Scholar was 2000; nevertheless, this criterion was not used for the papers from Scopus. Consequently, one paper was found from 1999.

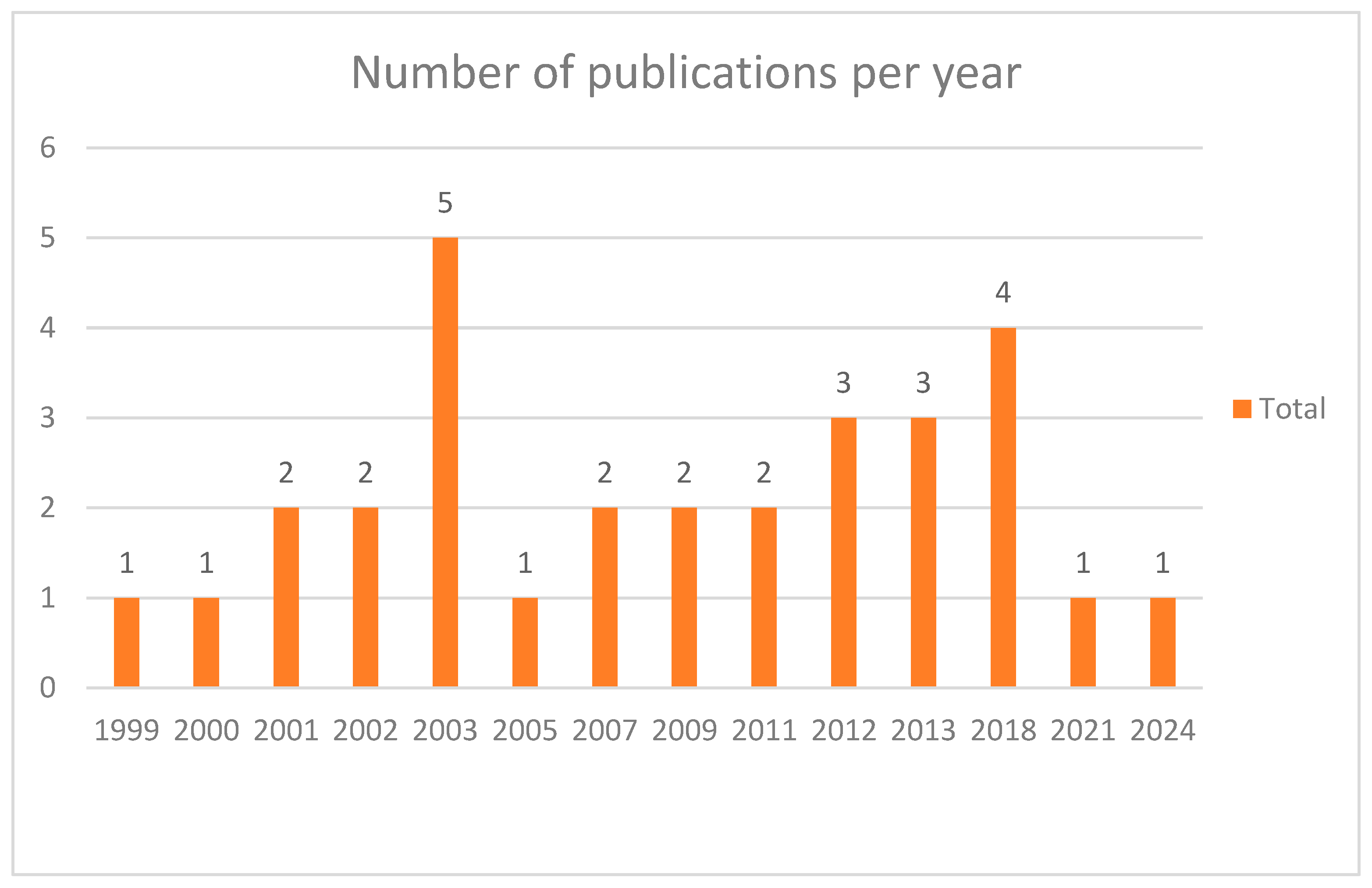
Figure 1 shows the trend in published papers related to this study on the state of the art. In actuality, researchers are still very interested in this subject, even though considerable research has been performed since 1986. Indeed, this constant interest is driven by the continuous competition between airports, airlines, and even countries, driving them to set up the most optimal hub locations for both passengers and cargo service providers.

3.1.2. Geography of Publications

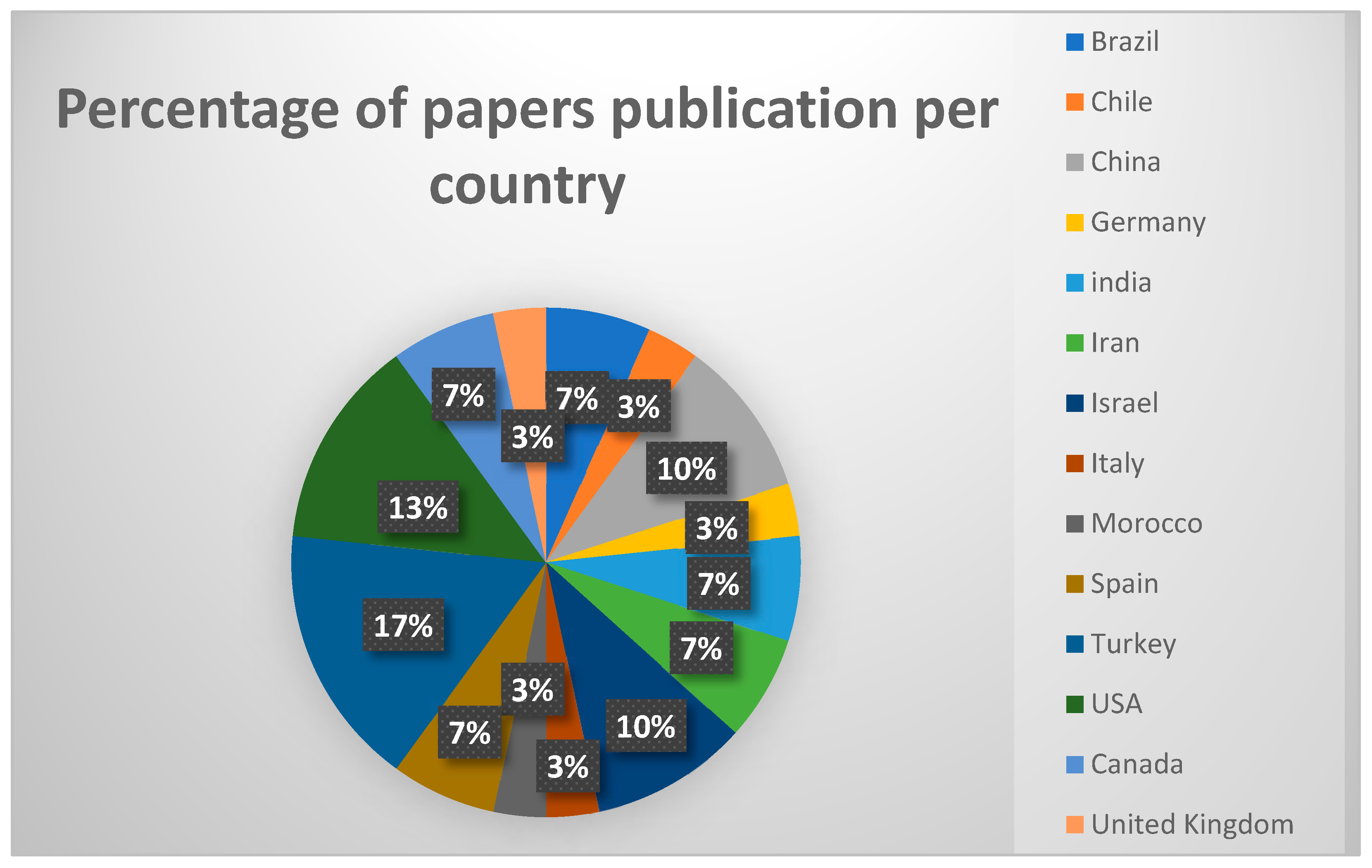
When analyzing the contributions of different countries to the subject, when authors from different countries collaborated on a paper, we chose the first author’s affiliated country. Figure 2 shows the percentage of publication of papers per country.

The papers studied within the scope of this review come from various countries all over the world, as shown in Figure 3. Nonetheless, Turkey is leading in terms of the number of publications. Indeed, 17% of the papers were produced by Turkish researchers, which is justified by the appeal of Istanbul as a major hub for diverse airline companies that benefit from establishing hub-and-spoke networks [7]. Next is the USA with 13%, noting that the deregulation of the local airline industry was a great motivator for hub-and-spoke research in 1978 [8]. China follows, as one of the major world producers and logistics platforms for its own air transportation activities, with 10% of publications. This interest is motivated by the fact that the Chinese air network is divided into six regions due to the large area covered. Notably, Chinese airports are categorized as national, regional, or local based on their network connectivity [9].

Israel and Iran, respectively, produced 10% and 7% of publications, confirming the importance of hub-and-spoke networks in the Middle East region. Spain, India, and Canada produced 7% of the publications. It is clear that, in general, African countries and even European countries are behind in terms of the number of publications related to the subject, with Morocco, Italy, the UK, and Germany only contributing one paper each (3%).

3.1.3. Publication Type

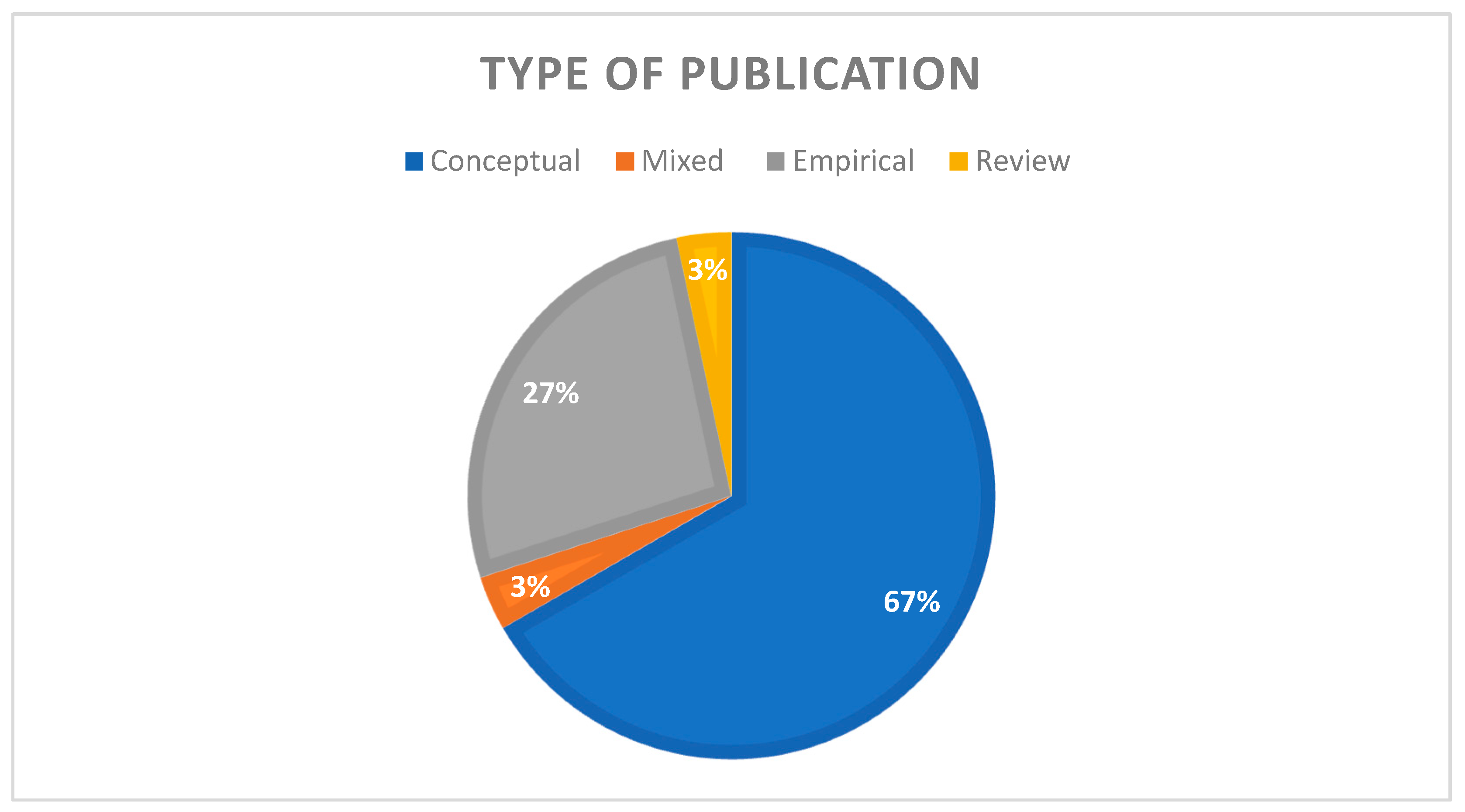
Figure 4 shows that the vast majority of the publications are conceptual (67%). This high percentage indicates that various hub-and-spoke network models still dominate the literature. A total of 27% of the publications are empirical, mainly with applications of existing theories and models for case studies and the analysis of specific contexts. Only 3% of the publications mixed empirical data and produced a new conceptual model. Finally, 3% of the publications are reviews, showing the importance of conducting thorough literature reviews on the matter.

3.2. Hub-and-Spoke Models in Air Transportation

Structural changes have been progressively implemented in air transportation networks over the years in different parts of the world. Indeed, US airlines were the first to adopt hub-and-spoke networks, mainly due to the deregulation of the aviation market in the USA in 1978. Then, European carriers followed by moving from the classical point-to-point PP model to the hub-and-spoke HS [10]. Different studies have approached the subject from multiple perspectives, either through modeling or resolution techniques.

Table 1. The literature reviewed regarding modeling, thematic, and computational aspects.

Reference	Modeling Approach	Dataset Used	Solver
[1]	Empirical study	-	-
[2]	Single-allocation hub-covering model	CAB	CPLEX
[3]	HS network with center-to-center directs	Federal Express AsiaOne airnetwork	CPLEX
[4]	Game theory	Boeing passenger demand data	-
[7]	Multi-center air transport model	-	GAMS
[8]	Game theory	ICAO	-
[9]	Capacitated p-hub median model	-	-
[10]	Empirical study	-	-
[11]	Stochastic programming model	China and Taiwan air freight market data	GAMS/OSL
[12]	Empirical study	-	-
[13]	Empirical study	-	-
[14]	N/A (Review)	-	-
[15]	Uncapacitated multiple allocation: branch-and-bound procedure	CAB and AP	CPLEX
[16]	Uncapacitated multiple allocation: mixed-integer linear programming	Turkey’s Air cargo market data (TAC) Turkish Air Cargo and Turkish Network Dataset	-
[17]	Game theory	CAB and AP	CPLEX, Gurobi
[18]	Uncapacitated multiple allocation: Benders decomposition	AP	CPLEX
[19]	Uncapacitated multiple allocation under congestion: heuristic	CAB	-
[20]	Uncapacitated multiple allocation under congestion: cutting plane approach and heuristic	CAB and TR	CPLEX
[21]	Hierarchical multi-hub location: mixed-integer programming	Turkish Network Dataset	CPLEX
[22]	Game theory	Passenger Demand Datasets of 1992	-
[23]	Game theory	ICAO	-
[24]	Game theory	-	-
[25]	Game theory	-	Standard Partial
[26]	Stylized model of network structure	-	-
[27]	Dynamic virtual HLP: metaheuristic approaches (ILS and HSA)	CAB and Turkish networks	CPLEX
[28]	Incomplete hub covering: variable neighborhood search	CAB	CPLEX
[29]	Empirical study	-	-
[30]	Uncapacitated multiple allocation: Benders decomposition	-	CPLEX
[31]	Capacitated hub location problem: Adaptive Large Neighborhood Search (ALNS)	Iran Air Organization for the year 2015	CPLEX
[32]	Empirical study	-	-

below presents the 30 articles reviewed on the chosen topic.

As competition is one of the main characteristics of the airline industry, we emphasize a specific model that addressed both competition and linear/nonlinear programming later on.

3.2.1. Planning and Scheduling in HLP

The planning and scheduling of routes in an air network either for cargo or passenger airlines are a crucial part of network design. Indeed, the hub location problem requires a strategic level of planning due to the decision-making involved [11].

References [1,11,12,13] handled scheduling decisions and the planning of an air network from a hub location problem perspective.

Reference [12] adopted the SMPSO algorithm to generate a network where the departure times guarantee the optimal filling ratio with the minimum connecting time. The QSI (quality of service index) is a decision-making factor for the multi-objective problem and is considered a beneficial parameter for any route (with the nodes of the network as departure stations).

Moreover, reference [1] approached the scheduling decision from a comprehensive economic analysis point of view. As a matter of fact, the study compared the flight frequencies of a hub-and-spoke (HS) and Fully Connected (FC) networks to mathematically prove that flight frequencies are higher in the former. Nonetheless, the high flight frequency in an HS network does not necessarily imply lower fares for customers (passengers or cargo), even if the cost per passenger/per kilo of cargo is lower in an HS network than in an FC network.

Additionally, for cargo operations, the seasonality in demand is a factor that affects many cargo airline businesses. Reference [11] addressed the effect of seasonal variations within the air freight market using a stochastic model rather than a deterministic one. This approach is very beneficial in planning and scheduling air networks.

3.2.2. The Allocation of Origins in the HLP

In addressing the hub location problem (HLP), either single or multiple origin points can be allocated to the hub nodes.

Reference [2] adopted a single-allocation model, while references [14,15,16] all adopted a multiple-allocation scheme while developing the hub location problem model. Finally, reference [17] suggested two different models: one based on single allocation and another based on multiple allocation.

Reference [2] concentrated only on the air cargo sector by suggesting a single-allocation hub-covering model that permits at most three hubs to be visited on a route.

Reference [14] reviews the novelty related to the hub location problem in general. It focuses on the heuristics developed on this topic, mainly those related to the multiple-assignment model. It also discusses how integer solutions can be reached using these heuristics.

References [15,18] both handled a specific part of the hub location problem: the uncapacitated multiple-allocation HLP. They both developed a computerized solution that enables the exact optimal solution to be reached within a reasonable amount of time.

Reference [16] focuses only on cargo operations while addressing the HLP. The authors developed a linear model related to the uncapacitated multiple-allocation HLP. The paper contains the results of the study in terms of the factors affecting the decision-making of a cargo hub location problem, including the “Trip cost, aircraft range, runway availability, and cargo traffic continuity”.

Reference [17] studies the hub location problem in terms of competition between airlines without using game theory frameworks, instead suggesting diverse network types: multiple-allocation and single-allocation networks. The mathematical formulations used are nonlinear integer programs. Two solutions are presented: one based on a mixed-integer second-order conic program and another based on Kelley’s cutting plane method. The performance of the resulting network was measured on the CAB and AP datasets.

3.2.3. Types of Hub-and-Spoke Networks

Reference [3] notes the difference between the following three types of hub-and-spoke air networks, specifically for cargo: 1. pure hub-and-spoke networks; 2. hub-and-spoke networks with pick-up stopovers and feeders; and 3. hub-and-spoke networks with center-to-center direct flights. Reference [3] concentrated on the economic effects of the third type (hub-and-spoke networks with center-to-center direct flights) to prove that this model requires a smaller fleet than the second type (hub-and-spoke networks with pick-up stopovers and feeders). Moreover, reference [9] focused on pure hub-and-spoke networks by studying the integral constrained p-hub median design problem, demonstrating the variations between the p-median and p-center, on the one hand, and p-hub, on the other hand.

References [19,20,21] focus on a cost-minimizing hub location problem. Reference [19] approaches the hub location problem in a specific context: a hub airport that becomes congested. In this situation, the authors indicate that these airports would be modeled as M/D/c queuing systems, before formulating a new hub location model focused on minimizing the total costs while taking the congestion factor into consideration. A distinction is made between two versions of the model: “First, the number of runways is fixed. Second, the number of runways is determined by the model itself”.

On the other hand, reference [20] considers stochastic demand and congestion to produce a model that minimizes all of the following costs: transportation, congestion, and total fixed costs.

Reference [21] compares the influence of the cost parameters on the location of an airport hub with their influence on a ground hub. The authors formulate a hierarchical multimodal HLP through a mixed-integer programming formulation.

3.2.4. Competition Factor in HLP

The competition between airlines and airports has become very strong since the 1990s, mainly through the introduction of hub-and-spoke network strategies [22].

References [4,17,22,23,24,25] approached the HLP from a competition perspective (either between airlines, airports, or even countries, or larger geographic zones). Three papers adopted different game theory models, and one paper adopted both a single- and multiple-allocation HLP model.

Reference [22] formulates a model structure that approaches the hub-and-spoke network design problem using a competitive framework. The analysis is based on a Nash best response game to search for a monopolistic and duopolistic equilibrium, mainly in the western European market.

Reference [4] presents a game theory framework in which the network design problem features an objective function that combines profit maximization and cost minimization. A competition analysis using the game theory framework suggested was performed, taking airline alliances and mergers into consideration as a tool to locate the optimal hub. The authors then try to determine equilibria in response to the common instinctive suggestion, noting that alliances between airlines can be surprisingly non-beneficial for some air networks.

Reference [23] presents a game theory framework from a spatial dimension. A competition analysis takes governmental and international deals into consideration, such as open skies policies.

Reference [26] studies the impact of uncertainty on the choice of whether to adopt a hub-and-spoke network model to prove whether the costs under low demand will be minimized in this scenario.

Reference [25] stands out from the articles that use game theory models by presenting models mostly adapted to real-life situations, aimed at airlines prioritizing profitability. Indeed, the authors hypothesized a game-theoretic approach realized in two stages: First, an airline will pick its network and choose whether to compete or not on an O/D service. Then, it will set three parameters at the same time—frequency, plane size, and price—while already knowing the strategy of its competitor in the first stage.

The game described in reference [25] can be played as follows: let S be the set of strategies of airlines within an HS network, where once the “connections are set, they cannot be changed within the game”. The initial strategy $S_0$ can be modeled as an integer linear program connecting spoke nodes to a chosen set of hub nodes based on a minimum distance criterion.

Let $d_{ij}$ be the distance between nodes $i$ and $j$. $x_i=0$ if no connection is set, $x_i=1$ if a single connection is set, $i_1$ is hub number 1, and $i_2$ is hub number 2, and ${\epsilon }_1-{\epsilon }_2$ is a variable that measures the solution’s balance.

$$\begin{array}{c}Minimise \left({\epsilon }_1+{\epsilon }_2\right)\varnothing +\sum _{\begin{array}{c}j=1\\ j\ne i_1, i_2\end{array}}^n\left[d_{i_{1}j}{x}_{i_{1}j}+d_{i_{2}j}{x}_{i_{2}j}\right] \\ x_{ij}\end{array}$$

(1)

subject to

$$x_{i_{1}j}+x_{i_{2}j}=1 \forall j, j\ne i_1, i_2$$

(2)

$${\sum }_{\begin{array}{c}j=1\\ j\ne i_1, i_2\end{array}}^n{x}_{i_{1}j} -{\sum }_{\begin{array}{c}j=1\\ j\ne i_1, i_2\end{array}}^n{x}_{i_{2}j} ={\epsilon }_1-{\epsilon }_2$$

(3)

$${\epsilon }_i\ge 0 , i=1, 2$$

(4)

$$x_{i_{1}j} , x_{i_{2}j} \in \left\{0 , 1\right\} \forall j, j\ne i_1, i_2$$

(5)

Different decision variables are also set and resolved, such as the utility function of the market share of the airline, its cost function, and its revenue function. As already explained, in the second stage of the game, each airline chooses the following at the same time to maximize its profit, while already knowing all of their competitors’ networks chosen in the first stage: frequency, plane size, and prices. Reference [25] assumes explicit competition and thus proposes an iterative process to obtain a sub-game perfect Nash equilibrium if it exists. Consequently, three different scenarios can be reached:

• A second stage sub-game Nash solution exists: The result would be a monopoly, oligopoly, or competitive market;
• A quasi-equilibrium is achieved: The convergence of the decision variables is partially achieved;
• No equilibrium exists: Convergence is not achieved.

Reference [25] argues that networks with low demand increase the possibility of a monopoly situation, but the oligopoly situation is likely to occur with enough demand levels.

3.2.5. Diverse Modeling Approaches for HLP

Reference [10] introduces two new parameters related to the hub-and-spoke network design: spatial and temporal dimensions. The Gini index and Freeman index are used for the spatial dimension, while the connectivity ratio is used for the temporal dimension. The paper presents a strategic comparison between the networks of LCC and FSC airlines.

Reference [27] developed a new mathematical model for the dynamic virtual hub location-routing problem (DVHLP). Inclement weather is a major factor that directly affects incapacitation in the hub allocation problem, which adds to the ability of the network to increase flexibility and demand. The CAB dataset was used to confirm the performance of the resulting network.

Reference [28] focuses on a specific part of the HLP, in which imprecise location demands are considered as variables. The authors developed a solution based on a variable neighborhood search (VNS) and validated the results through the CAB dataset.

Reference [29] compares two different solution approaches: continuous and discrete. In order to formulate a computerized experiment, a discretization heuristic and Voronoy diagram are used. While the discrete solution is based on applying the branch-and-cut method to the p-hub median model, the continuous solution is based on applying the hyperbolic smoothing technique to a min-sim-min model.

Reference [30] introduces a new notion related to the hub location problem (HLP) by differentiating between global and domestic flows. This is the gateway hub location problem (GHLP), in which global flows only enter or exit a geographic region through a gateway and local flows only enter or exit the region using hubs. The mathematical algorithm used is a mixed-integer programming formulation based on the Benders decomposition method.

Reference [31] approaches the hub location problem for an airline or airport from a capacity perspective, considering this parameter as a function of the arrival and departure of flights and not as a constant. The objective is to improve airport capacity in favor of the airline network through an algorithm called Adaptive Large Neighborhood Search (ALNS).

References [7,8,32] approach multi- and single-center air transport models of the hub location problem using different factors: “high speed train accessibility, green airport applications and the effects of the COVID-19 pandemic” [7], flight frequencies, and circle distances between airports. As examples, Federal Express (FedEx) and United Parcel Service (UPS) place importance on additional factors such as market centrality and railway or road transportation [32].

4. Conclusions

The design of an air transportation provider network requires strategic considerations. This paper reviews how the existing literature has examined the main part of this logistic issue—the hub location problem. The high number of papers produced on the subject does not necessarily mean that all mathematical models have been studied thoroughly. A simple reason behind the high number of papers is the infinite number of specific situations that an airline/airport/country could face depending on different factors. This study highlights that competition frameworks could be addressed in relation to the hub location problem through different mathematical approaches: competition and game theories and classical single- and multiple-allocation HLP models.

Moreover, the diversity of the modeling approaches may be crucial for decision makers when implementing an air network within a long-term strategy, whether they are locating an air cargo hub, calculating the number of runways, or choosing the air routes that would be most beneficial for the network.

Finally, as discussed above, the nature of the papers examined highlights the opportunity to perform a profound systematic literature review on the subject, starting at least from 2008 when the first detailed state-of-the-art study related to this subject [33] was published.