Abstract
The performance evaluation of production systems is essential for optimizing throughput caused by machine failures and operational constraints. In this study, we introduce an aggregation method designed to evaluate serial production lines (SPLs) that operate under the Slowdown Policy (SP). The SP dynamically adjusts machine service rates based on buffer levels, reducing blocking and ensuring a stable production rate. We propose an aggregation-based analytical approach that simplifies the evaluation of large-scale production systems while maintaining accuracy. To validate the method, a five-machine, four-buffer production line was analyzed, and the aggregation results were compared with those of a simulation. The results showed that our method provides a fast and good approximation of system performance.
1. Introduction
Throughput analysis is essential in the design, control, and optimization of production systems. However, these systems often suffer from inefficiencies due to machine failures, repair delays, and operational constraints. Failures interrupt production and maintenance delays increase downtime and repair costs, while blockages and starvation impact system performance. A blockage occurs when a machine cannot continue processing because the buffer is full, whereas starvation happens when a machine has no workpieces to process due to an empty buffer.
To mitigate these inefficiencies, control policies to reduce stoppages and improve system performance can be implemented. One such policy is the Slowdown Policy (SP) [1], which dynamically adjusts the service rate of machines based on the buffer level. The studied system consists of unreliable machines separated by buffers with limited capacity. Each machine is characterized by three exponentially distributed parameters: failure time, repair time, and processing rate. Under the SP, the processing rate of the machine is adjusted dynamically to reduce its blocking rate and idle time.
Given the complexity of such production systems, analytical evaluation is challenging for long lines. In this paper, we develop an aggregation method to estimate system performance efficiently.
The remainder of this paper is structured as follows: Section 2 presents a literature review on existing performance evaluation methods. Section 3 provides a short description of the Slowdown Policy control in a two-machine, one-buffer system. Section 4 introduces the aggregation method for evaluating multi-machine production lines operating under the SP. Section 5 presents an illustrative example where a five-machine, four-buffer production line was analyzed. Finally, Section 6 concludes the paper and suggests future research directions.
2. Literature Review
The evaluation of production system performance is influenced by several factors, such as system topology, operational balance, reliability, and system size. Simulation techniques are frequently employed to study complex systems and verify the accuracy of analytical models [2,3]. Analytical methods are favored for steady-state and transient performance assessment due to their computational efficiency [4]. However, their applicability is mostly limited to small-scale systems, typically comprising up to four machines [5]. Markov chain models are frequently employed in such cases but are computationally high [6]. More recently, artificial intelligence-based approaches have gained interest for estimating production line parameters and performance metrics.
On the other hand, for many years, approximate analytical techniques such as decomposition and aggregation methods have been designed to efficiently estimate key performance metrics (e.g., production rate and WIP) of different production line configurations. The decomposition method operates by decomposing the production system into smaller subsystems (two-machine, one buffer), assessing their individual starvation and blocking probabilities, and iteratively calculating performance metrics until convergence is reached. Due to its computational speed and accuracy, the decomposition method is considered a reliable approach for real-world applications. The aggregation method (AM) is another commonly employed approximate analytical technique. The AM operates iteratively by merging the initial two machines and an intermediate buffer into a single equivalent machine with modified failure and repair rates. This process continues until all machines are aggregated into a single equivalent unit. Aggregation-based equations provide fast approximations, making the AM suitable for practical industrial applications.
2.1. Exact Methods
Hunt (1956) [7] developed an equilibrium model based on Poisson arrivals and exponential processing times. Later, Muth (1973) [8] proposed mathematical models and queueing approaches for two- and three-machine systems. Buzacott (1968) [9] analyzed unreliable production lines without buffers. Later, an exact method to compute performance indicators for a two-machine, one-buffer system was developed in [10]. Berman (1982) [11] applied a Markovian method to compute production rates for two-machine, one-buffer systems with Erlang-distributed processing times. Other exact methods were introduced in later studies. In [12], the author analyzed reliable serial production systems with Poisson arrivals and exponential processing times. A Markov-based performance evaluation method for small systems (up to three machines) was proposed in [13]. Papadopoulos et al. (1989) [14] proposed iterative algorithms to analyze multi-station serial production lines, assuming exponential processing times. Other studies incorporated quality control and rework processes in serial production lines. For example, in [15], the authors analyzed reliable serial production systems with a quality control mechanism. The integration of quality and productivity measures in serial production lines was addressed by Cochran and Erol (2001) [16], who proposed models considering production rate and scrap rate together. In [17], the authors applied Gershwin’s (1994) [6] Markovian approach to evaluate serial production systems with two unreliable machines and one finite buffer. Tan (2003) [18] developed state-space models for pull-controlled manufacturing lines, while Kim and Gershwin (2005) [19] introduced Markov process models to analyze systems with finite and infinite buffer sizes by considering quality concept. Later, Tancrez et al. (2011) [20] applied phase-type distributions to approximate SPLs with finite buffers and general processing times. A linear programming method for SPLs with random processing times and finite buffers was proposed in [21]. Göttlich et al. (2015) [22] introduced sampling techniques using mixed-integer programming and differential equations to evaluate the performance of serial production lines. Fernandes et al. (2013a) [23] employed stochastic automata networks (SANs) to analyze reliable production lines with exponential service times. Their results demonstrated higher accuracy and efficiency compared with traditional Markovian queueing networks. Recent studies have integrated energy efficiency into SPL modeling. For example, energy consumption, WIP, and production rates in SPLs with Bernoulli machines were analyzed in [24]. Matta and Simone (2016) [25] analyzed unreliable SPLs with operation-dependent failures and time-dependent failures. Huang et al. (2020) [26] proposed a preventive maintenance approach integrating deep reinforcement learning for unreliable SPLs. Scrivano and Tolio (2021) [27] used Markov chains to analyze production lines incorporating manual and automated operations. With increasing focus on energy-efficient production, the authors of [28] developed an analytical model combining productivity and energy performance in two-machine SPLs with a buffer.
On the other hand, several studies have explored control policies in two-machine, one-buffer lines to optimize production efficiency. Gebennini et al. (2013, 2015) [29,30] introduced the restart policy, where the first machine idles when the buffer is full, reducing blockage frequency. Such policies help mitigate inefficiencies by dynamically adjusting machine operations. Nahas et al. (2025) [1] proposed a new control policy called the slowdown policy where the speed of the first machine is reduced to an optimal value when the buffer is full.
2.2. Decomposition Methods
Early studies on decomposition methods (DMs) for serial production lines (SPLs) focused on modeling systems with identical processing times [31]. Later, Hillier and Boling (1967) [32] evaluated the steady-state production rate and work-in-progress (WIP) for finite queue lines with Erlang-distributed processing times. In [33], the authors expanded decomposition methods by analyzing SPLs with Poisson arrivals and exponential processing times. Further advancements were made in the 1980s. Boxma and Konheim (1981) [34] applied a DM to tandem, split, and merge lines, using the equilibrium theorem. Altıok (1982) [12] developed a DM for reliable SPLs. Altıok and Perros (1987) [35] analyzed open queueing networks with Poisson arrivals and exponential processing times. Choong and Gershwin (1987) [36] proposed a DM for random failures and processing times, while Jafari and Shanthikumar (1987) [13] developed a DM for unreliable SPLs with limited buffers and scrapable parts. Dallery et al. (1988, 1989) [37,38] proposed two robust DM algorithms: the DDX algorithm for discrete material flows and an algorithm for continuous material transfer lines. These methods efficiently computed production rates while considering blocking and starvation. Jun and Perros (1990) [39] proposed a DM for finite-buffer SPLs, showing that a finite buffer in front of the first machine improved performance. The closed-loop production line with pallet constraints was analyzed in [40]. A matrix-based polynomial for single-buffer SPLs was introduced in [41]. Tolio et al. (1998) [42] highlighted unrealistic assumptions in classical analytical methods and proposed a DM variant considering multiple failure modes and finite buffers. Han et al. (1998) [43] integrated quality inspection machines into a DM.
Further studies addressed convergence issues and performance improvements. Dallery and Bihan (1999) [44] introduced the generalized exponential method, which improved accuracy by handling machine repair times via a two-moment approximation. Bihan and Dallery (2000) [45] extended this to a three-moment approximation, improving precision for SPLs with limited buffers. Later, a DM for non-homogeneous SPLs was proposed in [46]. In [47], a DM was applied to kanban-controlled serial production systems. Colledani et al. (2005) [48] expanded DMs to multi-product SPLs with different failure characteristics.
More recent work has adapted DMs to real-world manufacturing systems. Li (2004) [49] developed a decomposition-based approach for automotive production lines, validating results through simulations and industrial case studies. Alden et al. (2006) [50] reported that General Motors saved over $2.1 billion using production rate estimation. In [51], the authors integrated quality control machines into DM.
With growing interest in continuous flow models, Xia et al. (2012) [52] extended Dallery and Bihan’s [44] models for inhomogeneous SPLs, introducing a generalized exponential distribution approach. Shin and Moon (2014) [53] proposed a quasi-birth-and-death process-based algorithm for unbalanced SPLs.
More recently, Liberopoulos (2018) [54] introduced a DM for SPLs with geometrically distributed processing times. Wang et al. (2022) [55] analyzed Bernoulli serial lines, considering energy wastage from machine downtime. Helber et al. (2023) [56] introduced a neural network-based DM to handle the large expansion of machine state spaces in unreliable large SPLs.
2.3. Aggregation Methods
The aggregation method (AM) is a widely used approximate analytical approach for evaluating the performance of serial production lines (SPLs). De Koster (1987) [57] introduced the AM for large flow lines, extending the two-machine line analysis of [58,59]. In his study, he assumed exponentially distributed failure and repair times with finite buffers. Liu and Lin (1994) [60] later proposed an AM-based approach for unbalanced and reliable SPLs.
Several studies have applied AMs to real-world production lines. An AM-based performance estimation method for paint shops in automotive assembly was developed in [61], showing its efficiency through analytical formulas. Chiang et al. (2000) [62] applied AMs for unreliable SPLs using bottleneck detection. Colledani et al. (2008) [63] extended AM to multi-structure production lines, incorporating both serial and split machine configurations. Li (2013) [64] analyzed Toyota’s engine assembly system, transforming it into a serial line using AM to identify bottlenecks and optimize buffer allocation. Chen et al. (2016) [65] expanded the Markov-based model of Meerkov et al. [66] for multi-machine Bernoulli lines.
More recently, Wang et al. (2019) [67] applied AM for performance evaluation in SPLs, while Bai et al. (2021) [3] proposed an iterative AM-based method for multi-machine lines with finite buffers. An aggregation method for batch-discrete SPLs, incorporating Bernoulli reliability models was introduced in [68]. Wang et al. (2024) [69] proposed an AM-based analytical model to evaluate production rate and energy consumption in specialized SPLs.
3. Slowdown Policy for a Two-Machine System
Consider a production system consisting of two unreliable machines and a buffer with limited capacity placed between them (Figure 1). Machine M1 processes workpieces and transfers them to machine M2 with temporary storage in the buffer. Due to random failures and repairs, the system’s performance is influenced by blocking (when the buffer is full and M1 cannot continue working) and starvation (when the buffer is empty and M2 has no work to process).

Figure 1.
Two-machine production system with a finite buffer.
To improve system efficiency, Nahas et al. (2025) [1] introduced the Slowdown Policy (SP) control. This approach dynamically adjusts the service rate of machine M1 to reduce blocking while maintaining the desired production rate. The system operates in two modes: Standard (STD) and Slowdown (SWD) operation modes (Figure 2). In STD mode, machine M1 runs at its normal speed μ1, and the buffer level fluctuates between 0 and N − 1. When the buffer reaches full capacity (i.e., n = N), machine M1 slows down to a reduced service rate μ1∗, initiating the SWD mode. In this mode, machine M1 continues operating at μ1∗ until the buffer becomes empty (i.e., n = 0). At this point, the system switches back to STD mode, restoring machine M1 to its original speed μ1.
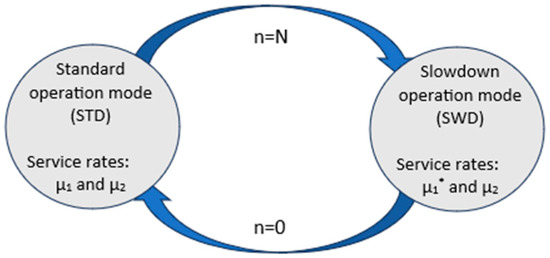
Figure 2.
Transitions between Standard (STD) and Slowdown (SWD) operation modes.
Figure 3 illustrates the state transition diagram of the two-machine production system under the Slowdown Policy (SP), detailing all possible states and transitions between the Standard (STD) and the Slowdown (SWD) operation Modes. Each state is represented by the quadruple (mode, n, α1, α2), where n is the buffer level, and α1, α2 indicate the operational status of machines M1; and M2;. The left side corresponds to STD mode, where M1; operates at its normal speed μ1, while the right side represents SWD mode, where M1; slows down to μ1* when the buffer is full (n = N). The system transitions between these states based on machine operations, failures, and repairs, with mode switching occurring when the buffer reaches its capacity limits: switching to SWD mode when full (n = N) and reverting to STD mode when empty (n = 0).
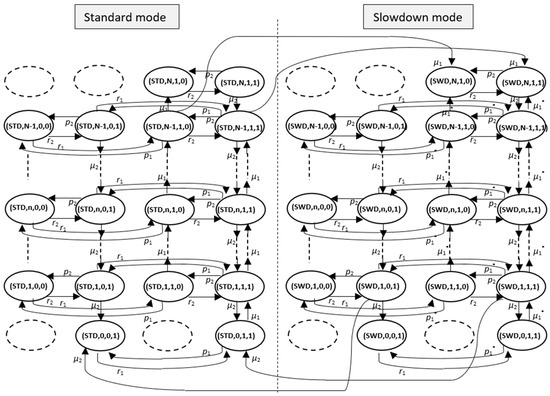
Figure 3.
State transition diagram of the two-machine, one buffer production system under the Slowdown Policy.
4. Aggregation Method for Multi-Machine Lines with the Slowdown Policy
Consider a production system consisting of n unreliable machines and (n − 1) intermediate buffers connected in series (Figure 4). Each machine is characterized by three parameters: average processing rate (μi), average repair rate (ri), and failure rate (pi).

Figure 4.
Serial production line.
The aggregation method is proposed to evaluate long production lines operating under the SP. Instead of analyzing individual machine−buffer interactions, the method iteratively combines adjacent machine−buffer pairs into artificial machines. Unlike traditional decomposition methods which rely on iteratively solving balance equations for each machine and buffer pair, the aggregation approach reduces the size of the system by replacing adjacent machine−buffer subsystems with equivalent machines. This leads to a significantly smaller state space and lower computational complexity. Decomposition methods can become computationally high due to convergence issues in the iterative process, especially in large systems [70]. In contrast, aggregation methods are generally simpler to implement and faster, making them well-suited for quick approximations in long production lines [71].
In our method, we apply downstream aggregation, beginning from the last machine Mn and moving backward to generate an equivalent machine representation. The subsystem [Mn−1, Bn−1, Mn] is replaced by an equivalent machine Mn−1,n. Once Mn−1,n is obtained, we aggregate it with Mn−2 and Bn−2. This process is repeated until we reach M1, at which point we obtain an equivalent machine representing the entire line.
Figure 5 provides a detailed breakdown of the operational states of M2 in the context of the Slowdown Policy. This policy separates the states into two distinct sections to define the equivalent failure rate, repair rate, and processing rate:
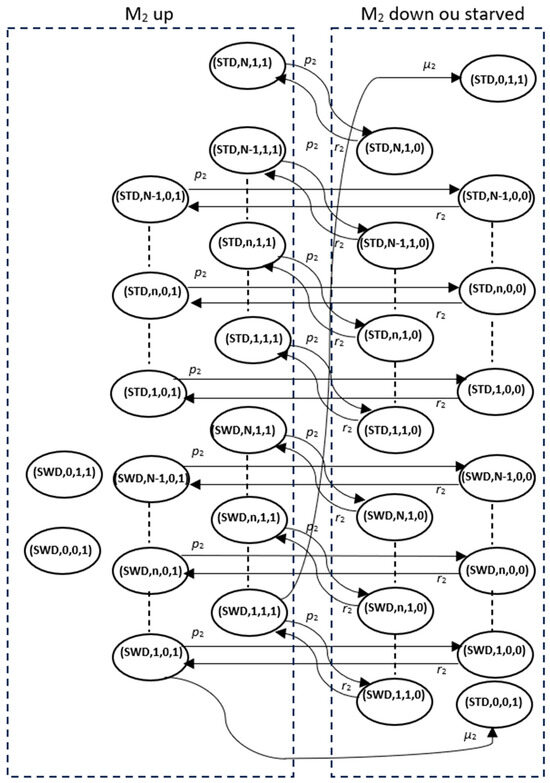
Figure 5.
State-transition diagram of two-machine, one buffer system under the Slowdown Policy.
- -
- M2 Up: This section includes all states where M2 is operational, either in Standard (STD) mode or Slowdown (SWD) mode.
- -
- M2 Down or starved: This section includes all states where M2 is down or starved, meaning it has failed and is undergoing repair or starved.
Using state probability distributions and transition rates, the equivalent machine parameters are derived as follows:
- -
- Equivalent Failure Rate
The failure rate of the equivalent machine Mi,i+1 considers both machine failures and slowdown effects:
where
pi+1 = probability that Mi+1 fails.
ps(0, 1, 1) = probability that Mi is in STD mode, Mi and Mi+1 are up, and the buffer is empty.
= processing rate in Slowdown mode.
= probability that Mi+1 is up and not starved.
- -
- Equivalent Repair Rate
The equivalent repair rate accounts for repairs and the slowdown effect when the buffer is empty:
where
ri+1= repair rate of Mi+1
ps(0,0,1) = probability that Mi is in STD mode and down, Mi+1 is up, and the buffer is empty.
pi = probability that Mi+1 is down or starved.
This expression adjusts the repair rate by incorporating the influence of the slowdown policy on buffer-starved and repair states.
- -
- Equivalent Processing Rate
Since Mi+1 determines the system throughput, the equivalent processing rate remains
where
µi+1 = processing rate of Mi+1
This reflects that under downstream aggregation, the effective throughput of the subsystem is determined by the last machine in the pair.
Probabilities are obtained from the steady-state distribution derived in [1]. Readers interested in the full derivation and probability computation can refer to that work for detailed explanations.
5. Illustrative Example: A Five-Machine Line
To validate the proposed method, a five-machine, four-buffer production line was analyzed. The system data are given in Table 1. The results obtained from the aggregation method were compared with discrete-event simulation outcomes. Buffers were varied from 10 to 30, and throughput performance with and without the SP was analyzed.

Table 1.
Data for the illustrative example.
The comparison (Table 2) shows that the aggregation method closely approximated simulation results obtained using ProModel version 10.2.0.3428 (a discrete-event simulation software), with deviations below 5% in most cases. These findings confirm that aggregation offers a computationally efficient alternative for evaluating production systems operating under the Slowdown Policy.

Table 2.
Comparison results.
6. Limitations
The proposed aggregation method relies on the assumption that machine failure, repair, and processing times follow exponential distributions. This Markovian framework simplifies the derivation of equivalent parameters. However, it may not accurately represent systems where time-to-failure or processing times show significant variability or deterministic distributions. In such cases, the performance estimates derived from the proposed aggregation method may deviate from real system behavior. Addressing these limitations would require the use of semi-Markov processes or simulation-based techniques, which we identify as important avenues for future research.
7. Conclusions
This study presents an aggregation-based methodology for evaluating multi-machine production lines operating under the Slowdown Policy. Initially developed for a two-machine system, the SP dynamically adjusts machine service rates to mitigate blocking and starvation effects, ensuring a more stable production flow.
The methodology was extended to longer production lines by iteratively aggregating adjacent machine-buffer pairs into equivalent machines. Using a downstream aggregation approach, we developed equivalent failure, repair, and processing rates, enabling a computationally efficient alternative to simulation.
The proposed aggregation method was validated through a five-machine system, comparing analytical results with discrete-event simulation outcomes. The results demonstrated that the aggregation approach closely approximated simulation results, with errors below 5% in most cases.
Ongoing work focuses on evaluating the method’s robustness by applying it to a large number of randomly generated production lines of lengths 3, 5, 7, and 10. Comparative studies with existing approaches are also planned. It is worth noting that this method relies on the assumption of exponential distributions for failure, repair, and processing times. Extending the framework to accommodate non-exponential behaviors remains an important direction for future research.
Author Contributions
Conceptualization, Z.N., N.E.-H. and N.N.; methodology, Z.N.; software, Z.N.; validation, Z.N., N.E.-H. and N.N.; formal analysis, Z.N.; investigation, Z.N., N.E.-H. and N.N.; resources, Z.N.; data curation, Z.N. and N.E.-H.; writing—original draft preparation, Z.N.; writing—review and editing, N.N. and N.E.-H.; visualization, Z.N.; supervision, N.E.-H. and N.N.; project administration, N.E.-H. and N.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nahas, Z.; El Hachemi, N.; Nahas, N. Performance Evaluation of an Unreliable Two-Machine System with Slowdown Policy. Comput. Ind. Eng. 2025, submitted.
- Diamantidis, A.C.; Lee, J.H.; Papadopoulos, C.T.; Li, J.; Heavy, C. Performance evaluation of flow lines with non-identical and unreliable parallel machines and finite buffers. Int. J. Prod. Res. 2020, 58, 3881–3904. [Google Scholar] [CrossRef]
- Bai, Y.; Tu, J.; Yang, M.; Zhang, L.; Denno, P. A new aggregation algorithm for performance metric calculation in serial production lines with exponential machines: Design, accuracy and robustness. Int. J. Prod. Res. 2021, 59, 4072–4089. [Google Scholar] [CrossRef]
- Tu, J.; Zhang, L. Performance analysis and optimisation of Bernoulli serial production lines with dynamic real-time bottleneck identification and mitigation. Int. J. Prod. Res. 2022, 60, 3989–4005. [Google Scholar] [CrossRef]
- Li, J.; Meerkov, S.M. Production Systems Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gershwin, S.B. Manufacturing Systems Engineering; Prentice Hall: Hoboken, NJ, USA, 1994; pp. 76–93. [Google Scholar]
- Hunt, G.C. Sequential arrays of waiting lines. Oper. Res. 1956, 4, 674–683. [Google Scholar] [CrossRef]
- Muth, E.J. The production rate of a series of work stations with variable service times. Int. J. Prod. Res. 1973, 11, 155–169. [Google Scholar] [CrossRef]
- Buzacott, J.A. Prediction of the efficiency of production systems without internal storage. Int. J. Prod. Res. 1968, 6, 173–188. [Google Scholar] [CrossRef]
- Gershwin, S.B.; Berman, O. Analysis of transfer lines consisting of two unreliable machines with random processing times and finite storage buffers. AIIE Trans. 1981, 13, 2–11. [Google Scholar] [CrossRef]
- Berman, O. Efficiency and production rate of a transfer line with two machines and a finite storage buffer. Eur. J. Oper. Res. 1982, 9, 295–308. [Google Scholar] [CrossRef][Green Version]
- Altıok, T. Approximate analysis of exponential tandem queues with blocking. Eur. J. Oper. Res. 1982, 11, 390–398. [Google Scholar] [CrossRef]
- Jafari, M.A.; Shanthikumar, J.G. An approximate model of multistage automatic transfer lines with possible scrapping of workpieces. IIE Trans. 1987, 19, 252–265. [Google Scholar] [CrossRef]
- Papadopoulos, H.T.; Heavey, C.; O’Kelly, M.E.J. Throughput rate of multistation reliable production lines with inter station buffers: (I) Exponential Case. Comput. Ind. 1989, 13, 229–244. [Google Scholar] [CrossRef]
- Jacobs, D.; Meerkov, S.M. Asymptotically reliable serial production lines with a quality control system. Comput. Math. Appl. 1991, 21, 85–90. [Google Scholar] [CrossRef]
- Cochran, J.K.; Erol, R. Performance modelling of serial production lines with inspection/repair stations. Int. J. Prod. Res. 2001, 39, 1707–1720. [Google Scholar] [CrossRef]
- Tolio, T.; Matta, A.; Gershwin, S.B. Analysis of two-machine lines with multiple failure modes. IIE Trans. 2002, 34, 51–62. [Google Scholar] [CrossRef]
- Tan, B. State-space modeling and analysis of pull-controlled production systems. In Analysis and Modeling of Manufacturing Systems; Springer: Boston, MA, USA, 2003; pp. 363–398. [Google Scholar]
- Kim, J.; Gershwin, S.B. Integrated quality and quantity modeling of a production line. OR Spectr. 2005, 27, 287–314. [Google Scholar] [CrossRef]
- Tancrez, J.S.; Chevalier, P.; Semal, P. Probability masses fitting in the analysis of manufacturing flow lines. Ann. Oper. Res. 2011, 182, 163–191. [Google Scholar] [CrossRef]
- Helber, S.; Schimmelpfeng, K.; Stolletz, R.; Lagershausen, S. Using linear programming to analyze and optimize stochastic flow lines. Ann. Oper. Res. 2011, 182, 193–211. [Google Scholar] [CrossRef]
- Göttlich, S.; Kühn, S.; Schwarz, J.A.; Stolletz, R. Approximations of time-dependent unreliable flow lines with finite buffers. Math. Methods Oper. Res. 2015, 83, 295–323. [Google Scholar] [CrossRef]
- Fernandes, P.; O’Kelly, M.E.J.; Papadopoulos, C.T.; Sales, A. Analysis of exponential reliable production lines using Kronecker descriptors. Int. J. Prod. Res. 2013, 51, 4240–4257. [Google Scholar] [CrossRef]
- Jia, Z.; Zhang, L.; Arinez, J.; Xiao, G. Performance analysis for serial production lines with Bernoulli machines and real-time WIP-based machine switch-on/off control. Int. J. Prod. Res. 2016, 54, 6285–6301. [Google Scholar] [CrossRef]
- Matta, A.; Simone, F. Analysis of two-machine lines with finite buffer, operation-dependent and time-dependent failure modes. Int. J. Prod. Res. 2016, 54, 1850–1862. [Google Scholar] [CrossRef]
- Huang, J.; Chang, Q.; Arinez, J. Deep reinforcement learning based preventive maintenance policy for serial production lines. Expert Syst. Appl. 2020, 160, 113701. [Google Scholar] [CrossRef]
- Scrivano, S.; Tolio, T. A Markov Chain model for the performance evaluation of manufacturing lines with general processing times. Procedia CIRP 2021, 103, 20–25. [Google Scholar] [CrossRef]
- Dong, H.; Li, J. Energy and productivity analysis in serial production lines with setups. IEEE Robot. Autom. Lett. 2022, 7, 7108–7115. [Google Scholar] [CrossRef]
- Gebennini, E.; Grassi, A.; Fantuzzi, C. The two-machine one-buffer continuous time model with restart policy. Ann. Oper. Res. 2015, 230, 69–92. [Google Scholar] [CrossRef][Green Version]
- Gebennini, E.; Gershwin, S.B. Modeling waste production into two-machine-one-buffer transfer lines. IIE Trans. 2013, 45, 591–604. [Google Scholar] [CrossRef]
- Vladzievskiĭ, A.P. The probability law of operation of automatic lines and internal storage in them. Avtom. I Telemekhanika 1952, 13, 227–281. [Google Scholar]
- Hillier, F.S.; Boling, R.W. Finite queues in series with exponential or Erlang service times-a numerical approach. Oper. Res. 1967, 15, 286–303. [Google Scholar] [CrossRef]
- Takahashi, Y.; Miyahara, H.; Hasegawa, T. An approximation method for open restricted queueing networks. Oper. Res. 1980, 28, 594–602. [Google Scholar] [CrossRef]
- Boxma, O.J.; Konheim, A.G. Approximate analysis of exponential queueing systems with blocking. Acta Inform. 1981, 15, 19–66. [Google Scholar] [CrossRef]
- Altıok, T.; Perros, H.G. Approximate analysis of arbitrary configurations of open queueing networks with blocking. Ann. Oper. Res. 1987, 9, 481–509. [Google Scholar] [CrossRef]
- Choong, Y.F.; Gershwin, S.B. A decomposition method for the approximate evaluation of capacitated transfer lines with unreliable machines and random processing times. IIE Trans. 1987, 19, 150–159. [Google Scholar] [CrossRef]
- Dallery, Y.; David, R.; Xie, X.L. An efficient algorithm for analysis of transfer lines with unreliable machines and finite buffers. IIE Trans. 1988, 20, 280–283. [Google Scholar] [CrossRef]
- Dallery, Y.; David, R.; Xie, X.L. Approximate analysis of transfer lines with unreliable machines and finite buffers. IEEE Trans. Autom. Control 1989, 34, 943–953. [Google Scholar] [CrossRef]
- Jun, K.P.; Perros, H.G. An approximate analysis of open tandem queueing networks with blocking and general service times. Eur. J. Oper. Res. 1990, 46, 123–135. [Google Scholar] [CrossRef]
- Frein, Y.; Commault, C.; Dallery, Y. Modeling and analysis of closed-loop production lines with unreliable machines and finite buffers. IIE Trans. 1996, 28, 545–554. [Google Scholar] [CrossRef]
- Yeralan, S.; Tan, B. Analysis of multistation production systems with limited buffer capacity part 1: The subsystem model. Math. Comput. Model. 1997, 25, 109–122. [Google Scholar] [CrossRef]
- Tolio, T.; Matta, A.; Jovane, F. A method for performance evaluation of automated flow lines. CIRP Ann. 1998, 47, 373–376. [Google Scholar] [CrossRef]
- Han, M.S.; Lim, J.T.; Park, D.J. Performance analysis of serial production lines with quality inspection machines. Int. J. Syst. Sci. 1998, 29, 939–951. [Google Scholar] [CrossRef]
- Dallery, Y.; Bihan, L.H. An improved decomposition method for the analysis of production lines with unreliable machines and finite buffers. Int. J. Prod. Res. 1999, 37, 1093–1117. [Google Scholar] [CrossRef]
- Bihan, H.; Dallery, Y. A robust decomposition method for the analysis of production lines with unreliable machines and finite buffers. Ann. Oper. Res. 2000, 93, 265–297. [Google Scholar] [CrossRef]
- Tempelmeier, H.; Bürger, M. Performance evaluation of unbalanced flow lines with general distributed processing times, failures and imperfect production. IIE Trans. 2001, 33, 293–302. [Google Scholar] [CrossRef]
- Krieg, G.N.; Kuhn, H. A decomposition method for multi-product kanban systems with setup times and lost sales. IIE Trans. 2002, 34, 613–625. [Google Scholar] [CrossRef]
- Colledani, M.; Matta, A.; Tolio, T. Performance evaluation of production lines with finite buffer capacity producing two different products. OR Spectr. 2005, 27, 243–263. [Google Scholar] [CrossRef]
- Li, J. Throughput analysis in automotive paint shops: A case study. IEEE Trans. Autom. Sci. Eng. 2004, 1, 90–98. [Google Scholar] [CrossRef]
- Alden, J.M.; Burns, L.D.; Costy, T.; Hutton, R.D.; Jackson, C.A.; Kim, D.S.; Kohls, K.A.; Owen, J.H.; Turnquist, M.A.; Veen, D.J.V. General motor increases its production throughput. Interfaces 2006, 36, 6–25. [Google Scholar] [CrossRef]
- Kim, J.; Gershwin, S.B. Analysis of long flow lines with quality and operational failures. IIE Trans. 2008, 40, 284–296. [Google Scholar] [CrossRef]
- Xia, B.; Xi, L.; Zhou, B. An improved decomposition method for evaluating the performance of transfer lines with unreliable machines and finite buffers. Int. J. Prod. Res. 2012, 50, 4009–4024. [Google Scholar] [CrossRef]
- Shin, Y.W.; Moon, D.H. Approximation of throughput in tandem queues with multiple servers and blocking. Appl. Math. Model. 2014, 38, 6122–6132. [Google Scholar] [CrossRef]
- Liberopoulos, G. Performance evaluation of a production line operated under an echelon buffer policy. IISE Trans. 2018, 50, 161–177. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y.; Jia, Z. Energy-efficient on/off control in serial production lines with Bernoulli machines. Flex. Serv. Manuf. J. 2022, 36, 103–128. [Google Scholar] [CrossRef]
- Helber, S.; Kellenbrink, C.; Südbeck, I. Evaluation of stochastic flow lines with provisioning of auxiliary material. OR Spectr. 2023, 46, 669–708. [Google Scholar] [CrossRef]
- De Koster, M.B.M. Estimation of line efficiency by aggregation. Int. J. Prod. Res. 1987, 25, 615–626. [Google Scholar] [CrossRef]
- Wijngaard, J. The effect of interstage buffer storage on the output of two unreliable production units in series, with different production rates. AIIE Trans. 1979, 11, 42–47. [Google Scholar] [CrossRef]
- de Koster, R.; Wijngaard, J. A continuous flow model for three production units in series with buffers. In DGOR, 14th Annual Meeting/Vorträge der 14. Jahrestagung; Springer: Berlin/Heidelberg, Germany, 1986; pp. 253–264. [Google Scholar]
- Liu, C.M.; Lin, C.L. Performance evaluation of unbalanced serial production lines. Int. J. Prod. Res. 1994, 32, 2897–2914. [Google Scholar] [CrossRef]
- Lim, J.T.; Meerkov, S.M.; Top, F. Homogeneous, asymptotically reliable serial production lines: Theory and a case study. IEEE Trans. Autom. Control 1990, 35, 524–534. [Google Scholar] [CrossRef]
- Chiang, S.Y.; Kuo, C.T.; Meerkov, S.M. DT-bottlenecks in serial production lines: Theory and application. IEEE Trans. Robot. Autom. 2000, 16, 567–580. [Google Scholar] [CrossRef]
- Colledani, M.; Gandola, F.; Matta, A.; Tolio, T. Performance evaluation of linear and non-linear multi-product multi-stage lines with unreliable machines and finite homogeneous buffers. IIE Trans. 2008, 40, 612–626. [Google Scholar] [CrossRef]
- Li, J. Continuous improvement at Toyota manufacturing plant: Applications of production systems engineering methods. Int. J. Prod. Res. 2013, 51, 7235–7249. [Google Scholar] [CrossRef]
- Chen, G.; Wang, C.; Zhang, L.; Arinez, J.; Xiao, G. Transient performance analysis of serial production lines with geometric machines. IEEE Trans. Autom. Control 2016, 61, 877–891. [Google Scholar] [CrossRef]
- Meerkov, S.M.; Shimkin, N.; Zhang, L. Transient behavior of two-machine geometric production lines. IEEE Trans. Autom. Control 2010, 55, 453–458. [Google Scholar] [CrossRef]
- Wang, F.; Ju, F.; Kang, N. Transient analysis and real-time control of geometric serial lines with residence time constraints. IISE Trans. 2019, 51, 709–728. [Google Scholar] [CrossRef]
- Liu, L.; Yan, C.B.; Li, J. Modeling, analysis, and improvement of batch-discrete manufacturing systems: A systems approach. IEEE Trans. Autom. Sci. Eng. 2021, 19, 1567–1585. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y.; Jia, Z.; Wang, G. Transient analysis of production performance and energy consumption in geometric flexible production systems. Expert Syst. Appl. 2024, 245, 123065. [Google Scholar] [CrossRef]
- Belmansour, A.-T. Contribution à la Modélisation, L’Analyse et L’Optimisation de Lignes de Production en Série Peu Fiables. Master’s Thesis, Université du Québec en Abitibi-Témiscamingue, Rouyn_Noranda, QC, Canada, 2007. [Google Scholar]
- Ouazene, Y. Méthodologie D’aide à la Conception Des Lignes de Production en Série: Application à L’Industrie Automobile. Ph.D. Thesis, Université de Technologie de Troyes, Troyes, France, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).