Abstract
An artificial neural network (ANN)-based decision support system model, which aggregates intuitionistic fuzzy matrix data using a recently introduced operator, is developed in this work. Several desirable features related to distance measures of aggregation operators and artificial neural networks, including the backpropagation method, are investigated to support the application of the proposed methodologies to multiple attribute group decision-making (MAGDM) problems using intuitionistic fuzzy information. A novel and enhanced aggregation operator—the Hamming–Intuitionistic Fuzzy Power Generalized Weighted Averaging (H-IFPGWA) operator—is proposed for weight determination in MAGDM situations. Numerical examples are provided, and various ranking techniques are used to demonstrate the effectiveness of the suggested strategy. Subsequently, an identical numerical example is solved without bias using the ANN backpropagation approach. Additionally, a novel algorithm is created to address MAGDM problems using the proposed backpropagation model in an unbiased manner. Several defuzzification operators are applied to solve the numerical problems, and the efficacy of the solutions is compared. For MAGDM situations, the novel approach works better than the previous ANN approaches.
1. Introduction
The purpose of artificial neural network organizations is to function as networks of parallel distributed computing. Neural networks have intrinsic characteristics that are analogous to those of biological neural networks and they are, by nature, Mathematical models of information processing. The basic processing units of neural networks are artificial neurons, or simply neurons. In an ANN, signals are transmitted between neurons via a coupler. To control its output signal, each neuron applies an activation function to its net input. A neural network is characterized by its architecture—the layout of the microcircuitry between neurons—its activation function, and its approach to assigning weight to the connections, which can be supervised or unsupervised. Artificial neural networks (ANNs) effectively handle uncertainty, nonlinearity, and high-dimensional data by learning complex patterns and relationships from input data. Their adaptive nature enables robust decision-making in diverse applications, including classification, optimization, and prediction.
Modern computers are accelerated sequential machines, in contrast to the brain’s wonderfully parallel structure. Arithmetic operations—sequential tasks that must be completed one after the other—are one example of the unique enterprises that the brain oversees. In the instance of visual or speech recognition problems, which are thought to be extremely parallel, the brain can easily and concurrently handle the intricacies, while a computer cannot manage such tasks as effectively. A biological neuron that works in the human brain is similar to the artificial neuron that has recently been developed. A neuron’s output can be either on or off, and it is entirely dependent on the inputs. The authors of [1,2,3,4,5,6,7,8,9] worked extensively on ANNs. Aggregation operators were designed and widely applied to MAGDM scenarios by the authors in [5,6,7,9,10,11,12]. Furthermore, the authors of [3,7,13,14] applied state-of-the-art techniques to tackle real-world problems involving fuzzy systems using machine learning applications. Although a significant number of ANN-related works have been conducted in the past, this paper will focus on the innovative field of ANNs with intuitionistic fuzzy sets and the use of the backpropagation approach, which has not yet been covered by many authors.
The Hamming–Intuitionistic Fuzzy Power Generalized Weighted Averaging (H-IFPGWA) operator is a novel and improved aggregation operator used in this paper to derive inputs for an adapted ANN model from [7]. In the past, the Power Generalized Weighted Averaging operator played a vital role in MAGDM problem-solving; in this work, it is enhanced with the Hamming distance to identify the closest alternatives to the attributes. The proposed ANN model appears to be more effective and reasonable, particularly when the decision-maker provides incomplete information about the problem statement. After processing the input using the novel backpropagated intuitionistic fuzzy ANN, the outcomes are evaluated for efficacy by contrasting them with those obtained using other ANN techniques and ranking strategies.
2. The Backpropagation Method for Artificial Neural Networks
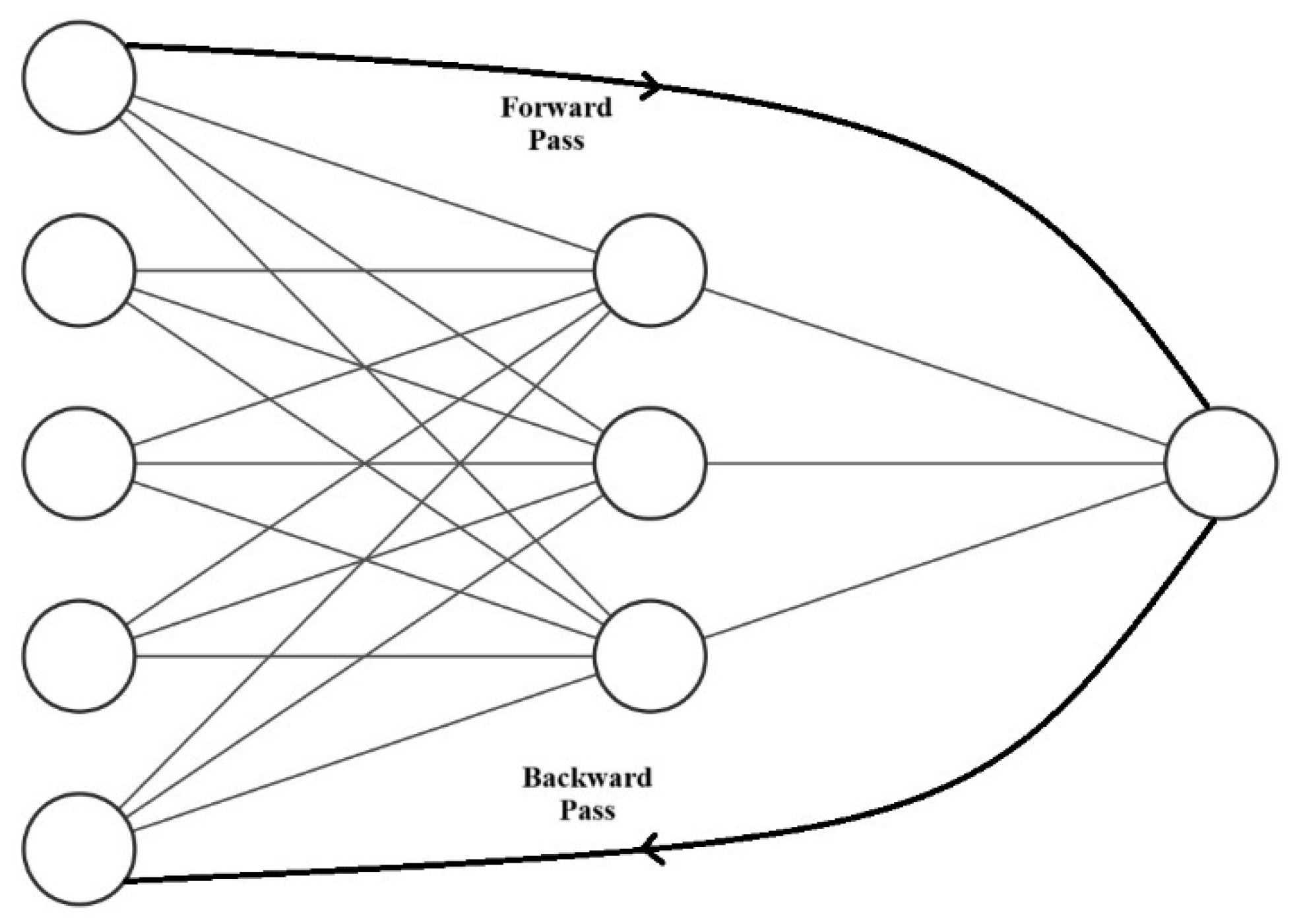
Since its inception, applications of artificial neural networks—or recursive nonlinear functions—have transformed machine learning. In this instance, proper training of a neural network is the most important step in producing a reliable model. The term “backpropagation”, commonly used in connection with this training, is difficult for most individuals unfamiliar with deep learning to understand. One of the crucial techniques utilized in ANN training is backpropagation. It is necessary to calculate the error rate of forward propagation and distribute the loss backward through the ANN layers in order to calibrate the weights during this network operation. The backpropagation phases are an essential component of any neural net training. It involves balancing the weights of a neural net according to the error rate achieved in the previous iteration, or epoch. Lower error rates, which occur during ANN weight vector calibration, improve the model’s generalizability and dependability. ANN’s backpropagation algorithm uses the chain rule to calculate the gradient of the loss function for a single weight which is evident from Figure 1. In contrast to an indigenous direct computational model—which computes the gradient but does not disclose how it is transmitted—the backpropagation skilfully computes one layer at a time and generalizes the calculation in the delta rule.
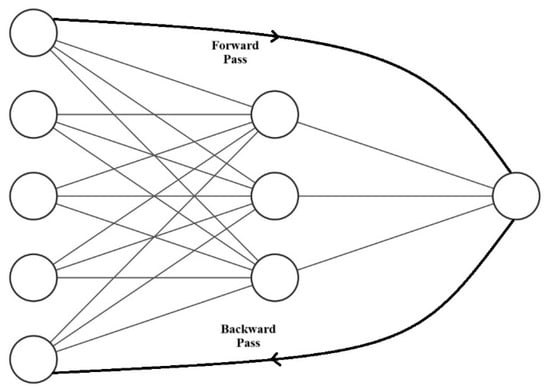
Figure 1.
A simple backpropagation architecture.
3. The Hamming–Intuitionistic Fuzzy Power Generalized Weighted Averaging (H-IFPGWA) Operator
In the following section, the Hamming–IFPGWA operator, which functions mainly based on the usual Euclidean distance metric for IFSs, is presented.
Definition 1.
Let be a cluster of Intuitionistic Fuzzy Numbers. Let
be the weighting vector of , where the weight vector has the property and Now, the novel and improvised operator called Hamming–Intuitionistic Fuzzy Power Generalized Weighted Average (H-IFPGWA) operator is proposed as follows: , where
Using mathematical induction on , the following can be observed:
where and is nothing but the support for from and possesses the following three properties:
(1) , (2) , (3) if , Sup () = 1–d (), where is the distance measure calculated using the Hamming Distance: d (,) = , where π = 1 − μ − ϒ.
Here, a few exclusive essentials of the operator are provided.
- (1)
- Suppose .
- (2)
- Suppose then .
- (3)
- Suppose , then
Theorem 1.
If
for all
then
Note: Support in the IFPGWA operator plays a crucial role in aggregating intuitionistic fuzzy information, balancing conflicting opinions, and improving the reliability of decision-making in MAGDM problems.
Theorem 2 (Commutative Property).
Let be any permutation of
, then
Theorem 3 (Idempotent Property).
Let
with
, then H-
Theorem 4 (Boundedness Property).
The is found to lie within the maximum and the minimum operators:
4. The Back-Propagated IFS-ANN with the H-IFPGWA Operator
| Pseudo-code for ANN with H-IFPGWA: Cn: n Matrix itemset of size k × m Input {An, Collection of n Intuitionistic Fuzzy Decision Matrices of size k } W = np.array([w1,w2,w3,w4,w5]) #weights Initialization //* Aggregation Phase*// Compute {Hamming-IFPGWA aggregator with the Initial Weight Vector} For (n = 1; An ∅; n++) do begin Generate {Individual Preference Intuitionistic Fuzzy Decision Matrices, Xn} //* Xn is the collection of Individual Preference IF-Decision Matrices *// Generate {Intuitionistic Fuzzy Attribute Weight Vector} //* The same H-IFPGWA is also used to derive the attribute weight vector *// While do {Defuzzify the IF column matrix into Fuzzy Column matrix} Generate {Collective Overall Preference Intuitionistic Fuzzy Decision Matrices the new Weight Vector, WT} //*Improvise the input vector by different Defuzzification functions , , , *// Input vector //* Back Propagation: Start*// Forward Pass: Calculate net input to each hidden layer: Learning Rate = 0.5 Error Calculation: Error = Target Output − Network output Backward Pass: (weights updating) ; Continue the Forward Pass with updated weights from Backward pass: Calculate net input to each hidden layer: Continue the weight updation until the error is minimized to a desired level //*Choosing the MAGDM best alternative*// Find {The Weighted Arithmetic Averaging (WAA) values between the alternatives} Find {The distance between WAA values and Net output} While Distance values Threshold do Generate {The best alternative} Output {Best Alternative(s) to be chosen} End. |
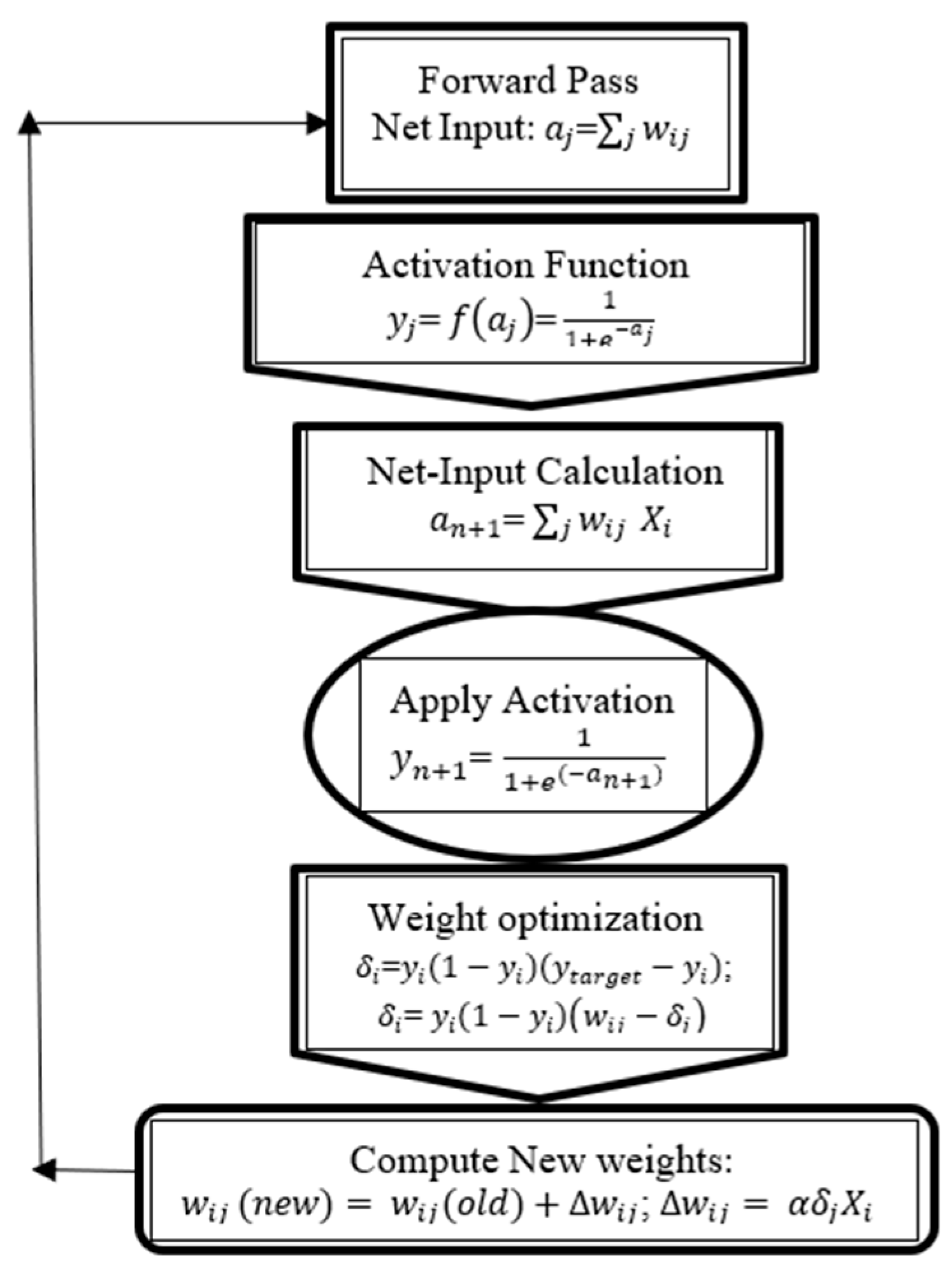
This pseudo-code algorithm works in three phases. Phase 1 is the aggregation phase, where the proposed H-IFPGWA operator combines all the given matrices with individual column matrices. Phase 2 involves the determining the attribute weight vector from the given decision matrices, which is used in the final phase of aggregation to convert the individual decision matrices into input for the ANN. Phase 3 consists of the forward and backward passes of the artificial neural network with backpropagation to decide the best alternative of the decision problem which is evident from the depiction given in Figure 2. The forward and backward passes are clearly depicted in the following flowchart.
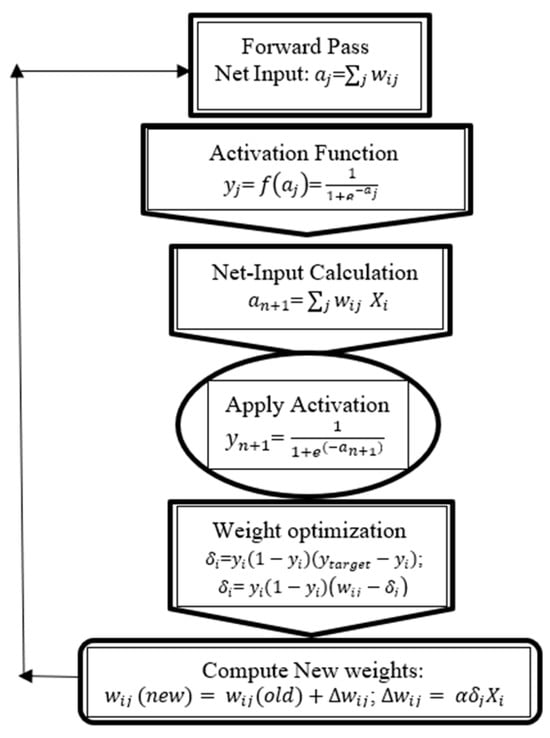
Figure 2.
Flow chart for backpropagation method.
5. Numerical Illustration for Backpropagated IFS-ANN withH-IFPGWA Operator
These days, the average person must invest money in a suitable company or plan. Consider an investment firm with five options for where to put its funds: Vehicles are the business of A1, beverages are the business of A2, software is the business of A4, heavy alloys are the business of A4, and oil and gas are the business of A5. The following four characteristics are considered: Risk analysis (G1), cash flow analysis (G2), liquidity analysis (G3), and debt and equity analysis (G4). Three experts have thoroughly examined this investment strategy challenge and subsequently offered their weighting vector. Their data are presented as decision matrices and are as follows:
Following the computations of BPIF-ANN, the results are as follows:
The H-IFPGWA values can be calculated for each data entry provided by the experts from the above three matrices. Suppose then
Similarly, all the other values from the above three matrices can be computed as collective overall matrices, as follows:
By defuzzifying the collective overall values using the identity , we obtain the input vector, as follows:
Assume the weight vector, (and permutation of for all the other stages) as follows:
= . Let the Target Output = 1.
Through computing the forward and backward passes and updating the weights, we can derive the output as recorded in Table 1 and Table 2.

Table 1.
Transforming vague values into fuzzy values.

Table 2.
Selection of best alternatives [7] by intuitionistic fuzzy ANN and different aggregation operators with/without hidden layers and different learning rules.
6. Discussion
Table 1 illustrates how this ANN model, which is based on the backpropagation technique, is used to convert intuitionistic fuzzy input into a fuzzy input vector using the three different defuzzification procedures based on the median membership grades. The collective matrix for which the ANN was used was supplied by the suggested H-IFPGWA operator, and the outcomes are shown in a table. Following the completion of weight updates, the network output is presented in Table 1. The maximum number of iterations is n=1000, though the decision-maker may choose to increase this to any large value of n. The best alternative is for one case and in the other two cases. The same numerical example was also illustrated by P-IFWG aggregation operator in [7], and the results were compared with existing ranking techniques. The choice of best alternative in [7] was also , when Delta and Perceptron Learning Rules were employed. Hence, using this new ANN algorithm proves to be a consistent method in line with the earlier proposed methods, which is clearly evident from the data presented in Table 1 and Table 2.
7. Conclusions
Using an enhanced aggregation operator for computing, a novel backpropagated model for MAGDM problem-solving is presented in this study. In order to solve the MAGDM problem, the new aggregation operator (H-IFPGWA) defined and used in this work advances the decision matrices to the next level of processing through an ANN. Lastly, the decision alternatives are ranked based on the updated weights of the ANN, following successful forward and backward passes. The model proposed in this paper was compared to the conventional MAGDM methods and techniques for addressing the same investment choice problem. Compared to the previous ANN-based method in [7], which employed different learning rules, the new ANN approach proves to be very effective, particularly in handling the complexities faced by decision-makers during the weight updating process in MAGDM situations. This MAGDM model, together with the proposed backpropagated ANN (implemented without any bias vector), can also be extended by including a bias vector, which is reserved for the future work.
Author Contributions
Conceptualization, methodology, validation, formal analysis, resources, supervision, project administration: J.R.P.D.; Writing—original draft preparation, writing—review and editing: W.A.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Atanassov, K.; Sotirov, S.; Pencheva, T. Intuitionistic Fuzzy Deep Neural Network. Mathematics 2023, 11, 716. [Google Scholar] [CrossRef]
- Hájek, P.; Olej, V. Intuitionistic Fuzzy Neural Network: The Case of Credit Scoring Using Text Information. In Engineering Applications of Neural Networks: EANN 2015, Rhodes, Greece, 25–28 September 2015; Iliadis, L., Jayne, C., Eds.; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2015; Volume 517. [Google Scholar] [CrossRef]
- Jekova, I.; Christov, I.; Krasteva, V. Atrioventricular synchronization for detection of atrial fibrillation and flutter in one to twelve ECG leads using a dense neural network classifier. Sensors 2022, 22, 6071. [Google Scholar] [CrossRef] [PubMed]
- Krasteva, V.; Christov, I.; Naydenov, S.; Stoyanov, T.; Jekova, I. Application of dense neural networks for detection of atrial fibrillation and ranking of augmented ECG feature set. Sensors 2021, 21, 6848. [Google Scholar] [CrossRef] [PubMed]
- Leonishiya, A.; Robinson, P.J. A Fully Linguistic Intuitionistic Fuzzy Artificial Neural Network Model for Decision Support Systems. Indian J. Sci. Technol. 2023, 16, 29–36. [Google Scholar] [CrossRef]
- Petkov, T.; Bureva, V.; Popov, S. Intuitionistic fuzzy evaluation of artificial neural network model. Notes Intuitionistic Fuzzy Sets 2021, 27, 71–77. [Google Scholar] [CrossRef]
- Robinson, P.J.; Leonishiya, M. Application of Varieties of Learning Rules in Intuitionistic Fuzzy Artificial Neural Network. In Machine Intelligence for Research & Innovations; Verma, O.P., Wang, L., Kumar, R., Yadav, A., Eds.; Lecture Notes in Networks & Systems; Springer: Singapore, 2024; Volume 832, pp. 35–45. [Google Scholar] [CrossRef]
- Sotirov, S.; Atanassov, K. Intuitionistic fuzzy feed forward neural network. Cybern. Inf. Technol. 2009, 9, 62–68. Available online: https://cit.iict.bas.bg/CIT_09/v9-2/62-68.pdf (accessed on 24 July 2024).
- Xu, Z.S.; Yager, R.R. Some Geometric Aggregation Operators Based on Intuitionistic Fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Leonishiya, A.; Robinson, P.J. Varieties of Linguistic Intuitionistic Fuzzy Distance Measures for Linguistic Intuitionistic Fuzzy TOPSIS Method. Indian J. Sci. Technol. 2023, 16, 2653–2662. [Google Scholar] [CrossRef]
- Yager, R.R.; Filev, D.P. Induced Ordered Weighted Averaging Operators. IEEE Trans. Syst. Man Cybern.-Part B 1999, 29, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Yager, R.R. The Power average operator. IEEE Trans. Fuzzy Syst. Man Cybern.-Part A Syst. Hum. 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, T.K.; Verma, O.P. Detection of Heart Failure by Using Machine Learning. In Machine Intelligence for Research & Innovations; Verma, O.P., Wang, L., Kumar, R., Yadav, A., Eds.; Lecture Notes in Networks & Systems; Springer: Singapore, 2024; Volume 832, pp. 195–203. [Google Scholar]
- Sharma, R.; Verma, O.P.; Kumari, P. Application of Dragonfly Algorithm-Based Interval Type-2 Fuzzy Logic Closed-Loop Control System to Regulate the Mean Arterial Blood Pressure. In Machine Intelligence for Research & Innovations; Verma, O.P., Wang, L., Kumar, R., Yadav, A., Eds.; Lecture Notes in Networks & Systems; Springer: Singapore, 2024; Volume 832, pp. 183–194. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).