Linear Quadratic Regulator Control of Rotary Inverted Pendulum Using Elvis III Embedded Platform †
Abstract
1. Introduction
2. Dynamic Model of Rotary Inverted Pendulum
3. LQR Controller Design
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Available online: https://www.ni.com/zh-tw/shop/model/ni-elvis-iii.html (accessed on 12 October 2024).
- György, K.; Dávid, L.; Kelemen, A. Theoretical study of the nonlinear control algorithms with continuous and discrete-time state-dependent Riccati equation. Procedia Technol. 2016, 22, 582–591. [Google Scholar] [CrossRef]
- Agarana, M.C.; Akinlabi, E.T. Lagrangian-Laplace dynamic mechanical analysis and modeling of inverted pendulum. Procedia Manuf. 2019, 35, 711–718. [Google Scholar] [CrossRef]
- Binz, R.; Aranovskiy, S. Iterative learning control strategy for a Furuta pendulum system with variable-order linearization. IFAC-PapersOnLine 2021, 54, 14–19. [Google Scholar] [CrossRef]
- Antonio-Cruz, M.; Hernandez-Guzman, V.M.; Merlo-Zapata, C.A.; Marquez-Sanchez, C. Nonlinear control with friction compensation to swing-up a Furuta pendulum. ISA Trans. 2023, 139, 713–723. [Google Scholar] [CrossRef] [PubMed]
- Nekoo, S.R. Digital implementation of a continuous-time nonlinear optimal controller: An experimental study with real-time computations. ISA Trans. 2020, 101, 346–357. [Google Scholar] [CrossRef] [PubMed]
- Acuña-Bravo, W.; Molano-Jiménez, A.G.; Canuto, E. Embedded model control for underactuated systems: An application to Furuta pendulum. Control. Eng. Pract. 2021, 113, 104854. [Google Scholar] [CrossRef]
- Nisar, L.; Koul, M.H.; Ahmad, B. Controller design aimed at achieving the desired states in a 2-DOF rotary inverted pendulum. IFAC-PapersOnLine 2024, 57, 256–261. [Google Scholar] [CrossRef]
- Safeea, M.; Neto, P. A Q-learning approach to the continuous control problem of robot inverted pendulum balancing. Intell. Syst. Appl. 2024, 21, 200313. [Google Scholar] [CrossRef]
- Tejado, I.; Torres, D.; Pérez, E.; Vinagre, B.M. Physical modeling based simulators to support teaching in automatic control: The rotatory pendulum. IFAC-PapersOnLine 2016, 49, 75–80. [Google Scholar] [CrossRef]
- Yavin, Y. Control of a rotary inverted pendulum. Appl. Math. Lett. 1999, 12, 131–134. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Workman, M. Digital Control of Dynamic Systems, 3rd ed.; Ellis-Kagle Press: Half Moon Bay, CA, USA, 1998. [Google Scholar]
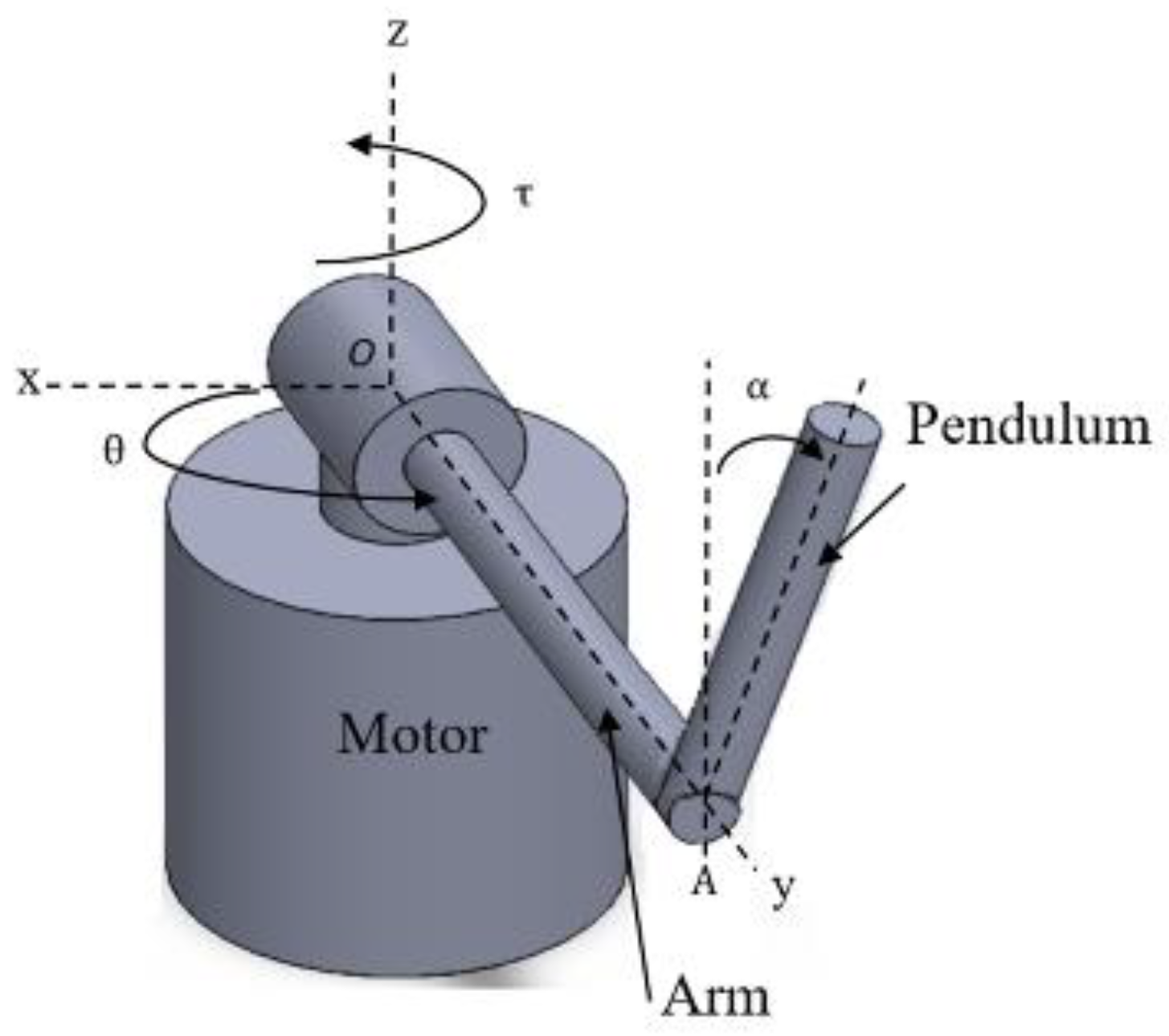


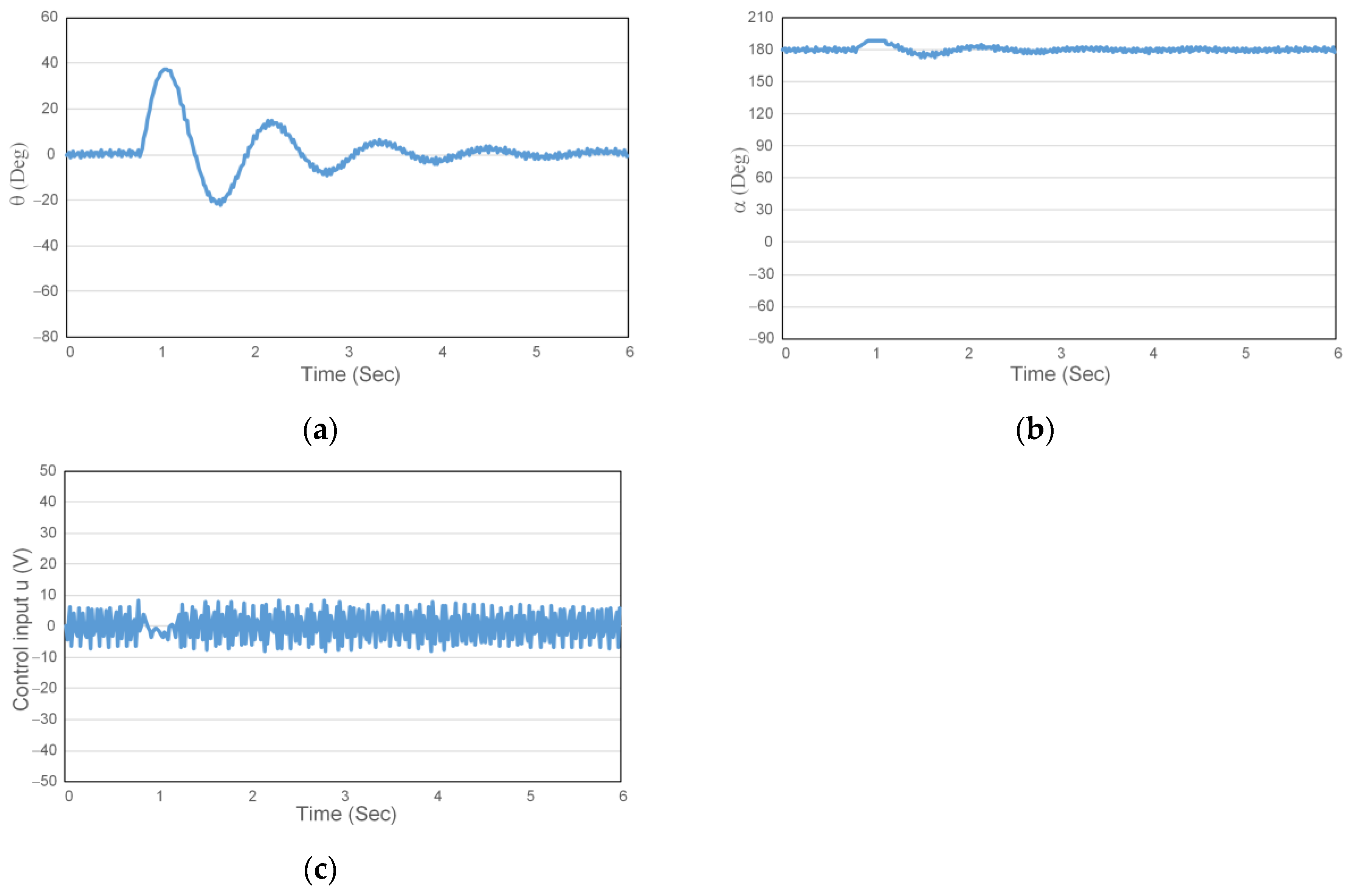
| Symbol | Description | Value | Unit |
|---|---|---|---|
| Lp | Swing bar length | 0.08504 | m |
| mp | Swing bar mass | 0.01724 | Kg |
| Lr | Swing arm length | 0.10602 | M |
| mr | Swing arm mass | 0.06046 | Kg |
| g | Gravity | 9.81 | m/s2 |
| Jp | Equivalent inertia of the swing rod | 0.00003143 | kg·m2 |
| Jr | Equivalent inertia of rotating arm | 0.00067416 | kg·m2 |
| C1 | The distance from the pivot point O to the center of mass G1 of the rotating arm | 0.01606 | M |
| C2 | The distance from the pivot point A to the center of mass G2 of the swing rod | 0.04321 | M |
| Kb | Back electromotive force | 0.16344417 | V·s/rad |
| Kt | Motor torque constant | 0.16344417 | N·m/A |
| Ra | Armature resistance | 6.15 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, M.-H.; Huang, J.-Q.; Tsai, Y.-H.; Chang, C.-C.; Chen, C.-Y. Linear Quadratic Regulator Control of Rotary Inverted Pendulum Using Elvis III Embedded Platform. Eng. Proc. 2025, 92, 46. https://doi.org/10.3390/engproc2025092046
Lin M-H, Huang J-Q, Tsai Y-H, Chang C-C, Chen C-Y. Linear Quadratic Regulator Control of Rotary Inverted Pendulum Using Elvis III Embedded Platform. Engineering Proceedings. 2025; 92(1):46. https://doi.org/10.3390/engproc2025092046
Chicago/Turabian StyleLin, Ming-Hung, Jun-Qi Huang, Yao-Hung Tsai, Chun-Chieh Chang, and Cheng-Yi Chen. 2025. "Linear Quadratic Regulator Control of Rotary Inverted Pendulum Using Elvis III Embedded Platform" Engineering Proceedings 92, no. 1: 46. https://doi.org/10.3390/engproc2025092046
APA StyleLin, M.-H., Huang, J.-Q., Tsai, Y.-H., Chang, C.-C., & Chen, C.-Y. (2025). Linear Quadratic Regulator Control of Rotary Inverted Pendulum Using Elvis III Embedded Platform. Engineering Proceedings, 92(1), 46. https://doi.org/10.3390/engproc2025092046





