1. Introduction
The integration necessity of disruptive technologies is considered to play a crucial part in the achievement of more energy-efficient, climate-friendly, and sustainable aviation. This is underlined in studies [
1] discussing the shortcomings of evolutionary improvements in aircraft components to fulfill international targets on the aviation climate impact. The interaction complexity of novel concepts, such as hybrid propulsion systems, and the potential use of hydrogen fuel or fuel cells, require the consideration of such technologies as early as the conceptual design phase. Furthermore, the data scarcity implies not only the inherent design uncertainties, but also unknown information on external factors concerning the systems’ operation. These include, for example, the difficulty in predicting operating costs due to energy price fluctuations, political preferences, or infrastructure availability. Hence, an analysis of the solution space under the consideration of uncertainties is necessary, including a robustness assessments of the solutions against fluctuations.
In this context, necessity arises not only to achieve optimal integration of novel concepts, but also to augment the reliability of uncertain results in this regard. Additionally, this implies the use of a system modeling approach which allows for uncertain estimations of design parameters and system performance, therefore excluding purely qualitative modeling methods. These aims reflect the latest developments of the Advanced Morphological Approach (AMA) [
2], which represents a structured conceptual design method focused on complex engineering solutions such as civil aircraft.
1.1. The Advanced Morphological Approach as a Conceptual Design Process
So far, the definition of aircraft configurations has relied predominantly on previous experience and brainstorming [
3]. The fundamental literature on engineering design has come to a general consensus on a common process structure for the generation of new concepts [
4,
5,
6]:
Exploration and functional decomposition of the problem;
Analysis of the isolated sub-problems and study of the component interconnections;
Structural synthesis of the engineering solution (combination of selected solutions of the sub-problems).
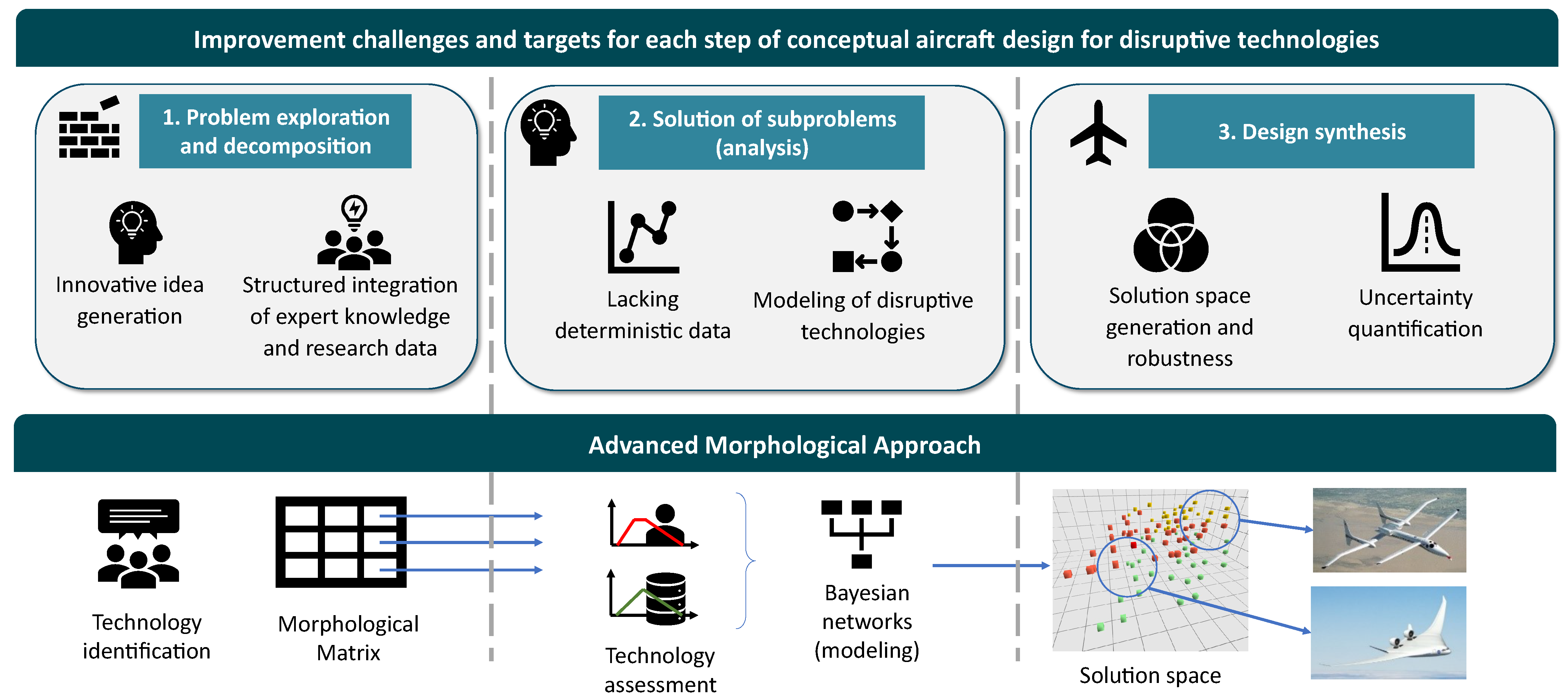
When applying this to conceptual aircraft design, a number of challenges and potential improvement targets can be identified for each stage. The AMA allows us to address each of these in the manner shown in
Figure 1. In order to enhance the generation of unconventional ideas and go beyond the designer’s own experience, the concept of the classical Morphological Analysis [
7,
8] is used as the AMA’s kernel. It is a creativity technique dating back to the 1950s [
9] which suggests the functional decomposition of a design problem. It is defined in a morphological matrix (MM) with system attributes such as rows and their alternative implementations (options) as columns, therefore fulfilling the purpose of the first stage of conceptual design. The second one is conducted by assessing the technological options. Initially, this has been done by eliciting qualitative expert judgments for given criteria and aggregating these in order to compensate for the lacking test data on novel technologies. Subsequently, the Analytical Hierarchy Process (AHP) was used to model the design system and obtain global evaluations of the options for a set of higher- and lower-level criteria [
10,
11]. Finally, design solutions were synthesized by combining the MM options and their calculated assessments into a solution space.
These achieved milestones in the definition of a structured conceptual design process yielded an initial framework for the generation and relative comparison of complex engineering solutions. However, these depended heavily on subjective expert opinions on a qualitative evaluation scale, thus remaining rough estimations of the configuration’s performance. In this context, a study has been conducted to select tools that introduce a more detailed design and uncertainty quantification [
12]. The results suggested replacing the AHP with system modeling based on Bayesian networks (BNs), which would allow for a more reliable approximation of design parameters and uncertainty propagation. In this way, it will pave the way for robustness analysis of the solution space.
The current paper suggests a novel framework structure for conceptual aircraft design which integrates AMA and BNs for semi-quantitative system modeling.
Figure 1.
Identification of the challenges in conceptual aircraft design and the corresponding AMA steps aiming to address these. Aircraft image sources: [
13,
14].
Figure 1.
Identification of the challenges in conceptual aircraft design and the corresponding AMA steps aiming to address these. Aircraft image sources: [
13,
14].
1.2. Objectives
The key objectives of the current paper are defined as follows:
Structured integration of uncertainty propagation in conceptual aircraft design.
Positioning and verification of BNs in conceptual aircraft design:
As a semi-quantitative approach for system modeling;
For uncertainty modeling and propagation;
For handling lacking data on disruptive technologies.
Investigation of solution space robustness analysis in combination with BNs.
The results of this paper serve the long-term purpose of combining expert knowledge and limited research data to deal with data scarcity for unconventional configurations.
2. Fundamentals
2.1. Bayesian Networks
Previous work [
11,
12,
15] has shown the wide variety of uncertainties inherent to aircraft design, especially in its conceptual design phase. As stated in Reference [
12], this could be achieved by applying BNs, which allow for the probabilistic modeling of system parameters, their relationships, and the uncertainty propagation.
Bayesian inference is based on the premise that each event (or in the case of product design, each design parameter) cannot be described by a single deterministic value. It rather reflects the world’s imperfections and can therefore be modeled as a probability distribution [
16]. These depend on one’s knowledge of the parameter, which could initially be subjective or uninformed (denoted as prior
) and subsequently updated by a number of observations (also denoted as observed data
y). This key process in Bayesian inference is modeled in Equation (
1) [
16].
The aim is to obtain an updated probability distribution
based on the observations
y (e.g., measurements, calculations, etc.) which is supposed to improve the prior belief
. This could be applied to the nodes of an acyclic directed graph, where each node represents a probabilistic or a deterministic variable. The variables are with predefined relationships. Since in most cases there is no analytical solution to Equation (
1) for complex graphs, the current approach to estimating the posterior distributions is Markov Chain Monte-Carlo (MCMC) sampling [
17].
2.2. Selected Use Case
Since the aim of this paper lies in the integration of uncertainty propagation and solution space robustness analysis, an existing design use case and its data were taken as its basis. This was the work of Marciello et al. [
18], who had investigated hybrid-electric designs for more sustainable regional aircraft under consideration of technology forecasts on power electronics and storage systems. In total, eight aircraft were derived in [
18] from an ATR 42-600-like baseline for technology performance estimations in the short (2025–2035), medium (2035–2045), and long term (2045–2050+). These integrated different propulsion concepts: the conventional internal combustion engine (ICE), hydrogen-powered fuel cells (Polymer Electrolyte Membrane Fuel Cells (PEMFCs) or Solid-Oxide Fuel Cells (SOFCs)), and batteries. The team behind Reference [
18] conducted mission step simulations to estimate the fuel efficiency, emissions, and performance of the different configurations for a design range of 600 nmi (1111.2 km) and a typical range of 200 nmi (370.4 km), able to carry a 4750 kg design payload (equivalent to 50 passengers). In the context of the AMA design process, the aircraft configurations simulated in [
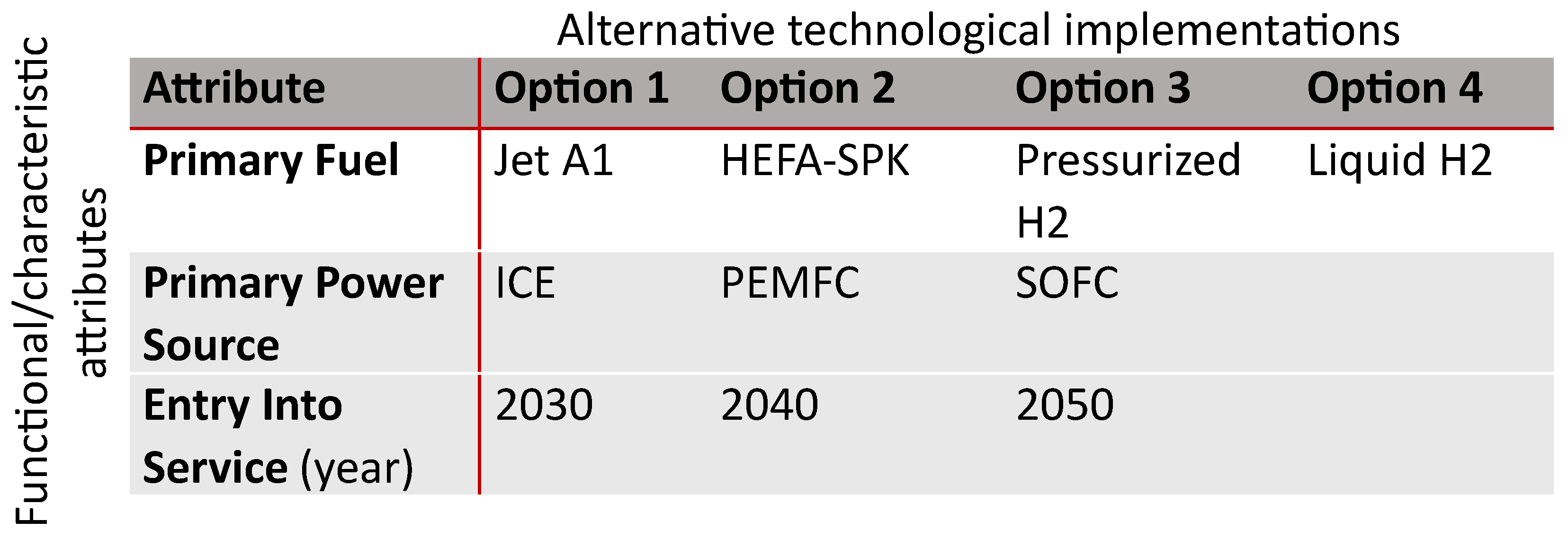
18] represent different combinations of the MM options defined in
Figure 2, and span the solution space.
3. Methodology
In order to fulfill the defined objectives (
Section 1.2), the developed approach in this work implemented a system model as a BN, used the data from Reference [
18], added uncertainties, and propagated those through the model. This allowed us to obtain and visualize uncertainties for the different design solutions, and to investigate the suitability for robustness analysis. Each step of the workflow is outlined in the following subsections.
3.1. Problem Definition and Decomposition; Dataset Definition
According to the AMA process, the configurations analyzed in Reference [
18] have been decomposed and summarized in an MM (
Figure 2). The available data from Reference [
18] allowed us to create a dataset of 16 data points in total. These comprise eight configurations for two mission ranges of 200 nmi and 600 nmi. The parameters included mass breakdowns, fuel quantities (kerosene, sustainable aviation fuel (hydroprocessed esters and fatty acid synthetic paraffinic kerosene, HEFA-SPK), or hydrogen), fuel, and battery energy (for the entire mission). Furthermore, Reference [
18] outlined assumptions on powertrain efficiencies, battery energy densities, and fuel cell power densities, which originated from technology forecasts.
3.2. System Modeling with a Bayesian Network
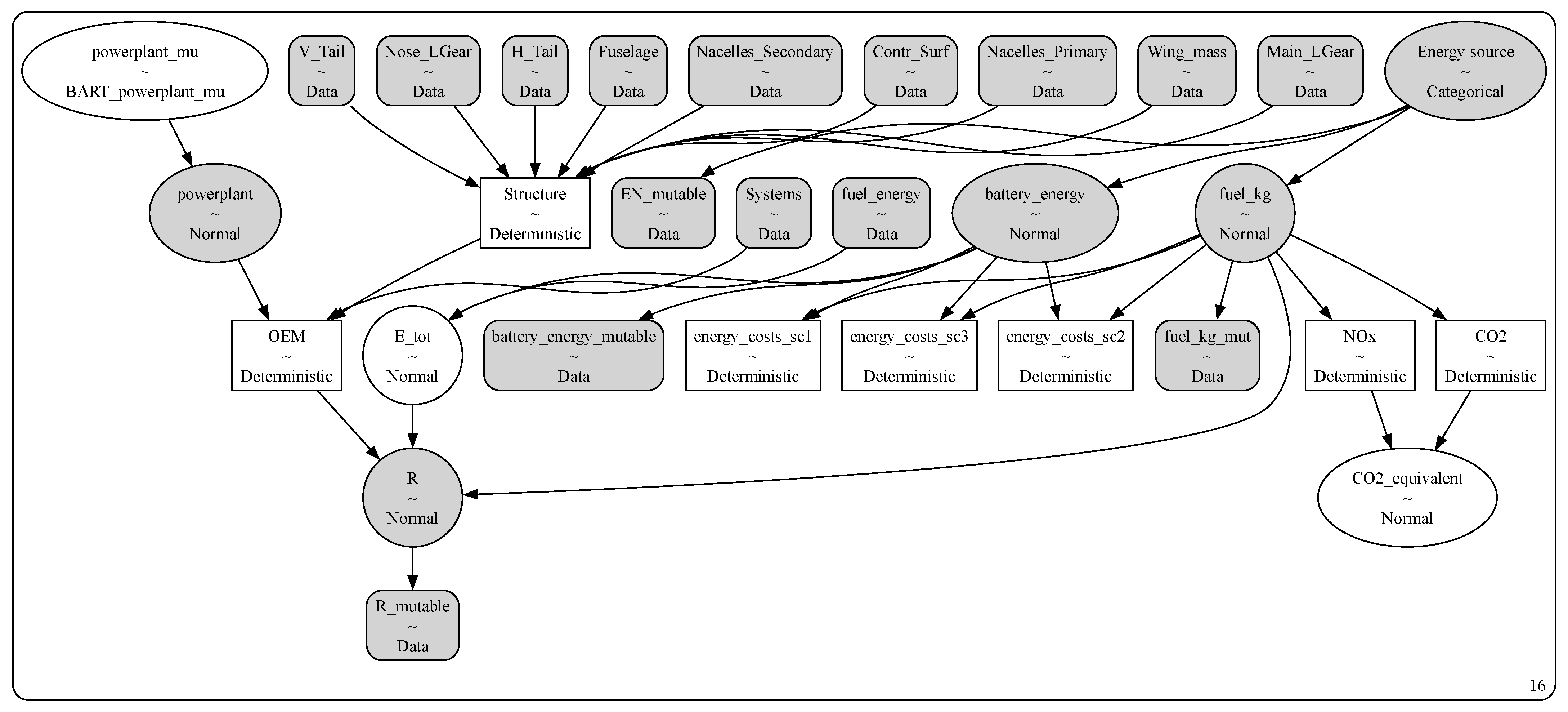
The BN structure and probabilistic inference were implemented in the Python 2 programming language with the probabilistic programming library PyMC [
19]. A visualization of the developed BN generated by the PyMC library is depicted in
Figure 3. The nodes represent different variables, with their names and types as upper and lower labels, respectively. Thus, variables marked as “Normal” were modeled probabilistically with a normal distribution; “Data” stands for datapoints without added uncertainty, allowing us to define variable values in order to make predictions; “Deterministic” stands for calculated variables with defined equations with no additional uncertainty.
In most cases, the node relationships were approximated with available equations, reflecting the physics behind the variable, e.g., the aircraft range calculation with the Breguet equation or its variations for hybrid-electric aircraft, as per Reference [
20]. The influence of the selected energy sources on the design was represented by defining a categorical variable and corresponding probability distributions for the child nodes depending on the energy source category. Another way to model complex relationships was to include a probabilistic decision tree model to reflect the nonlinear influence of the powerplant type on powerplant mass. This was done by applying the Bayesian additive regression trees method implemented in the PyMC-BART library [
21].
The defined BN structure does not pretend to embody a detailed and precise model of an aircraft, and therefore integrates rough approximations of the design parameters of interest. The main purpose of this BN was to take existing aircraft design data, add uncertainty to the variables, model the variable relationships in a probabilistic manner, and propagate the uncertainties through the defined system.
3.3. Solution Space Generation and Visualization
The subsequent step of the AMA allowed for solution space generation by building option combinations from the MM (
Figure 2) which corresponded to the design solutions from the derived dataset. For this purpose, probabilistic inference was conducted by applying MCMC sampling and propagating the variable uncertainties in the BN for each option combination. This allowed for the derivation of probability distributions of the defined target values, which are the total mission energy
, the mission energy costs, and the CO
2-equivalent operational mission emissions.
4. Results
4.1. Model Quality Assessment
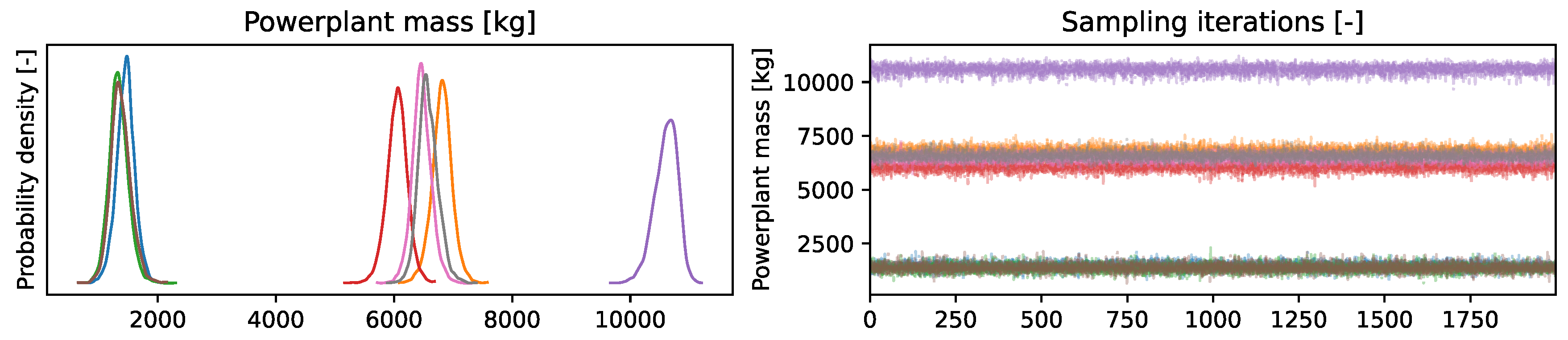
The verification of the BN model quality consisted of three major steps, which were conducted for the developed BN: a prior predictive check (quality of the model before seeing the data), a convergence assessment, and a posterior predictive check (quality of the model after seeing the data). The left diagram in
Figure 4 serves as an example of the last step and shows the posterior distributions of the powerplant mass for each configuration. One observes the mean variation depending on the types of primary fuel and the primary and secondary power sources—the means roughly correspond to the powerplant mass values given in Reference [
18]. The right side of
Figure 4 depicts the sampled value at each step within the MCMC algorithm. It confirms the estimated means and uncertainties by revealing the oscillation of each sample around the respective means.
4.2. Solution Space
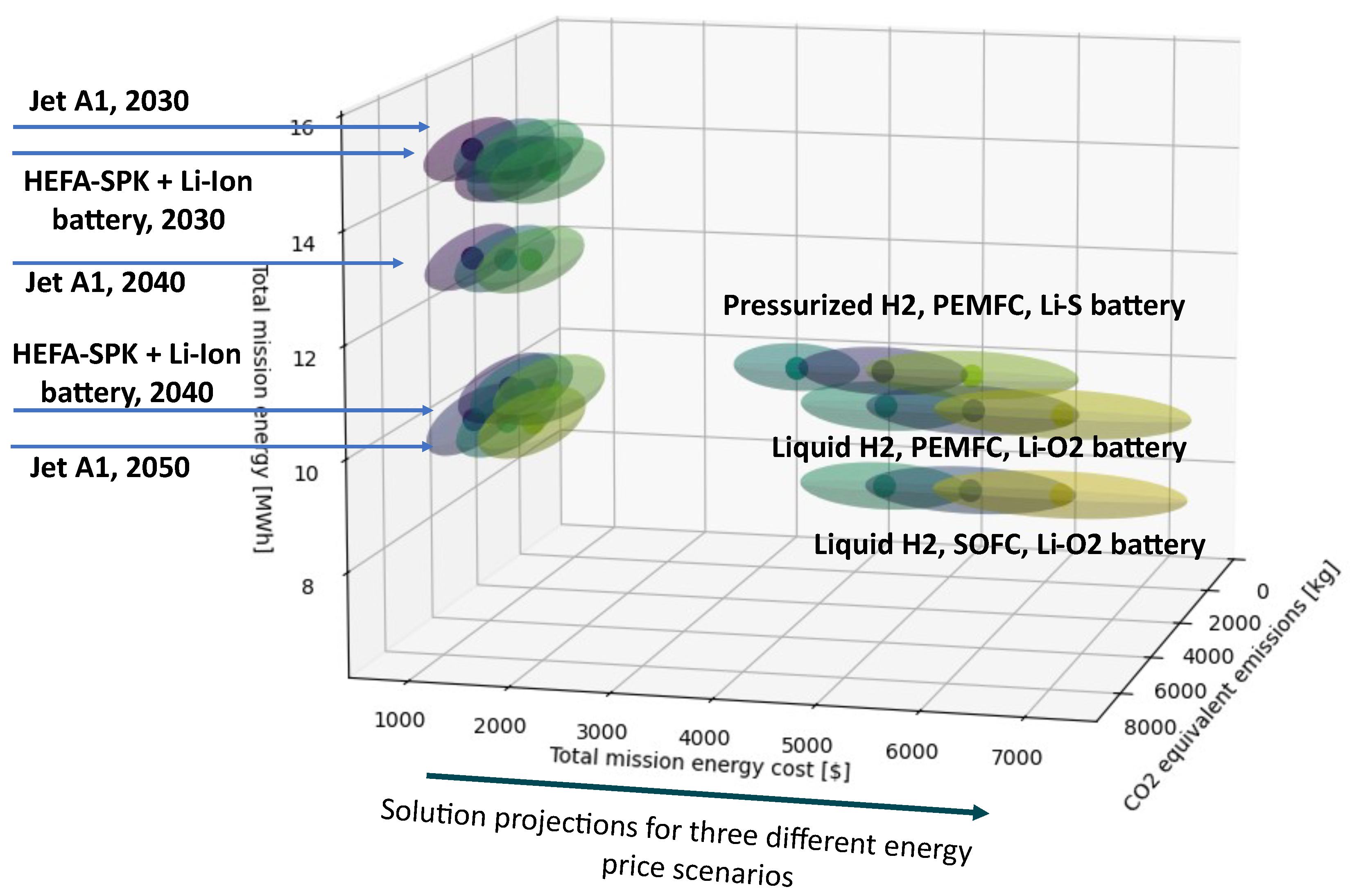
The generated solution space is visualized in
Figure 5, which positions the configurations along the axes describing total mission energy, total mission energy cost, and CO
2-equivalent emissions. In total, 24 datapoints are depicted—8 unique option combinations from the MM, which are varied for the three energy cost scenarios. The ellipsoids encircling the datapoints represent the uncertainties resulting from the probability propagation in the BN. One distinguishes eight clusters, each containing datapoints of the same configurations for the three energy cost scenarios. The observations fulfill initial expectations: newer technology (later entry into service) yields more energy-efficient aircraft, as well as zero operational CO
2 and NO
x emissions (incorporated into the CO
2-equivalent).
5. Discussion
Since the current study aimed to test the suitability of BNs for uncertainty propagation and solution space robustness analysis, the structure of the BN was kept rather simple to focus on certain parameters. Some variables kept the constant original data without introducing new uncertainty in order to focus on the parameters of interest and the target values. In this context, the model quality requirements to converge and fit the data have been fulfilled. Another main task of BNs is to make predictions on unseen data. Although this is outside of the current scope, the defined model would allow for the generation of novel concepts given unseen data. For example, the input of updated battery data (battery energy, mass, etc.) and the corresponding uncertainties would yield updated values for the rest of the parameters.
The benefit of the BN for the assessment of design robustness can be seen in the same figure. The large uncertainty intersections indicate lacking significance for proper decision-making in this area of the solution space.
6. Conclusions
An accelerated and reliable assessment of disruptive concepts is vital to accelerate the entry into service of more efficient aircraft and the achievement of climate goals. Low- and high-fidelity analyses of novel aircraft are computationally expensive and are not always applicable to components with a lower technology readiness level. In this context, the AMA is used as a structured conceptual design process to combine research data and expert knowledge for the innovative idea generation. The necessity for an increase in detail on design solutions and more reliable uncertainty modeling resulted in the integration of BNs into the AMA framework. The purpose of this work is to verify the use of BNs within the AMA and the approach’s suitability for conceptual aircraft design.
In this context, data from Reference [
18] were used, which consist of mass, emissions, and some mission performance values for ATR 42-600-like aircraft, which included different propulsion configurations—ICE, hybrid-electric, and fuel-cell-based. Subsequently, a BN structure was developed, aiming to estimate the total mission energy, the CO
2-equivalent emissions, and the energy cost for three energy price scenarios. The Bayesian inference was conducted through MCMC probability distribution sampling and uncertainty propagation. Subsequently, the model quality was confirmed with convergence and posterior predictive checks. Finally, a solution space was generated by plotting different concepts and their corresponding uncertainties. This allowed for the visualization of their robustness and the identification of different solution clusters.
While the added parameter uncertainties were exemplary, this work verifies the potential of BNs in conceptual aircraft design for multiple purposes. Firstly, it offers a reliable propagation of parameter uncertainties through the modeled system. Secondly, unlike other machine learning algorithms, it does not constitute a black box, i.e., BN is transparent regarding parameter probability definitions, as well as their relationships. Thirdly, it paves the way to more advanced solution space robustness analyses. Fourthly, it allows for the modeling of complex parameter relationships, e.g., through decision trees or categorical variables. Finally, BNs are well suited to the hypothesis and the approach of the AMA, which aims to take advantage from both expert knowledge and scarce research data in order to deal with lacking data on disruptive technologies. These steps are planned for execution in future, more detailed BNs.
Author Contributions
Conceptualization, V.T.T., D.R., and A.B.; methodology, V.T.T. and D.R.; software, V.T.T.; validation, V.T.T. and A.B.; formal analysis, V.T.T.; investigation, V.T.T.; resources, D.R. and A.B.; data curation, V.T.T.; writing—original draft preparation, V.T.T. and D.R.; writing—review and editing, D.R. and A.B.; visualization, V.T.T.; supervision, D.R. and A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 443831887.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available on demand.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytical Hierarchy Process |
| AMA | Advanced Morphological Approach |
| BN | Bayesian network |
| HEFA-SPK | hydroprocessed esters and fatty acid synthetic paraffinic kerosene |
| ICE | internal combustion engine |
| Li-Ion | lithium-ion |
| Li-O2 | lithium-air |
| Li-S | lithium-sulfur |
| MCMC | Markov Chain Monte-Carlo |
| MM | morphological matrix |
| PEMFC | polymer electrolyte membrane fuel cell |
| SOFC | solid-oxide fuel cell |
References
- The Shift Project; SUPAERO DECARBO. Pouvoir Voler en 2050: Quelle Aviation dans un Monde Contraint? (Flying in 2050: What Future for Aviation in a Constrained World?). Technical Report. 2021. Available online: https://theshiftproject.org/wp-content/uploads/2021/03/Pouvoir-voler-en-2050_ShiftProject_Rapport-2021.pdf (accessed on 22 July 2021).
- Bardenhagen, A.; Rakov, D. Analysis and Synthesis of Aircraft Configurations During Conceptual Design Using an Advanced Morphological Approach; Deutsche Gesellschaft für Luft- und Raumfahrt—Lilienthal-Oberth e.V.: Bonn, Germany, 2019. [Google Scholar] [CrossRef]
- Sadraey, M.H. Aircraft Design: A Systems Engineering Approach; Aerospace Series; Wiley: Chichestet, West Sussex, UK, 2013. [Google Scholar]
- Goel, V.; Pirolli, P. The structure of Design Problem Spaces. Cogn. Sci. 1992, 16, 395–429. [Google Scholar] [CrossRef]
- Pahl, G.; Wallace, K.; Blessing, L.; Pahl, G. (Eds.) Engineering Design: A Systematic Approach, 3rd ed.; Springer: London, UK, 2007. [Google Scholar]
- Taura, T. Basic Principles of Conceptual Design. In Creative Design Engineering; Elsevier: Amsterdam, The Netherlands, 2016; pp. 119–129. [Google Scholar] [CrossRef]
- Ritchey, T. General Morphological Analysis. A General Method for Non-Quantified Modelling; Swedish Morphological Society, 2002; Available online: https://www.swemorph.com/pdf/gma.pdf (accessed on 13 March 2025).
- Zwicky, F. Discovery, Invention, Research—Through the Morphological Approach; The Macmillan Company: Toronto, ON, Canada, 1969. [Google Scholar]
- Zwicky, F. Morphology and Nomenclature of Jet Engines. Aeronaut. Eng. Rev. 1947, 6, 49–50. [Google Scholar]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Structured Expert Judgment Elicitation in Conceptual Aircraft Design. Aerospace 2023, 10, 287. [Google Scholar] [CrossRef]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Enhancement Opportunities for Conceptual Design in Aerospace Based on the Advanced Morphological Approach. Aerospace 2022, 9, 78. [Google Scholar] [CrossRef]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. A Morphological Analysis of Methods for Conceptual Aircraft Design under Uncertainties. In Proceedings of the 34th Congress of the International Council of the Aeronautical Sciences (ICAS), Florence, Italy, 9–13 September 2024. Available online: https://www.icas.org/ICAS_ARCHIVE/ICAS2024/data/papers/ICAS2024_1169_paper.pdf (accessed on 13 March 2025).
- Thomas, C.; NASA. Proteus EC03-0085-17: Proteus in Flight over Rosamond Dry Lakebed. 2003. Available online: https://www.dfrc.nasa.gov/Gallery/Photo/Proteus/HTML/EC03-0085-17.html (accessed on 9 December 2024).
- NASA; The Boeing Company. File: Boeing Advanced Blended Wing Body Concept 2011 (Cropped).jpg—Wikipedia. 2011. Available online: https://en.m.wikipedia.org/wiki/File:Boeing_advanced_blended_wing_body_concept_2011_%28cropped%29.jpg (accessed on 9 December 2024).
- Thunnissen, D.P. Uncertainty Classification for the Design and Development of Complex Systems. In Proceedings of the 3rd Annual Predictive Methods Conference, Newport Beach, CA, USA, 16–17 June 2003. [Google Scholar]
- Koski, T.; Noble, J.M. Bayesian Networks: An Introduction, 1st ed.; Wiley Series in Probability and Statistics; Wiley: Chichester, UK, 2009. [Google Scholar]
- Van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte–Carlo sampling. Psychon. Bull. Rev. 2018, 25, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Marciello, V.; Di Stasio, M.; Ruocco, M.; Trifari, V.; Nicolosi, F.; Meindl, M.; Lemoine, B.; Caliandro, P. Design Exploration for Sustainable Regional Hybrid-Electric Aircraft: A Study Based on Technology Forecasts. Aerospace 2023, 10, 165. [Google Scholar] [CrossRef]
- Abril-Pla, O.; Andreani, V.; Carroll, C.; Dong, L.; Fonnesbeck, C.J.; Kochurov, M.; Kumar, R.; Lao, J.; Luhmann, C.C.; Martin, O.A.; et al. PyMC: A modern, and comprehensive probabilistic programming framework in Python. PeerJ Comput. Sci. 2023, 9, e1516. [Google Scholar] [CrossRef] [PubMed]
- De Vries, R.; Hoogreef, M.F.M.; Vos, R. Range Equation for Hybrid-Electric Aircraft with Constant Power Split. J. Aircr. 2020, 57, 552–557. [Google Scholar] [CrossRef]
- Quiroga, M.; Garay, P.G.; Alonso, J.M.; Loyola, J.M.; Martin, O.A. Bayesian additive regression trees for probabilistic programming. arXiv 2023. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).