Design of Maximally Permissive Controllers for Solving Deadlock Problems in Flexible Manufacturing Systems ^†

Abstract

Industry 5.0 aims to integrate humans and machines to achieve greater productivity, personalization, and sustainable development in the production process. Built on the foundation of Industry 4.0 which emphasizes automation, digitalization, and intelligent production processes, Industry 5.0 highlights the importance of human resources in modern manufacturing. Robotic arms have replaced traditional manpower, particularly in flexible manufacturing systems. However, integrating advanced machinery into workflows has increased competition in terms of securing resources, resulting in frequent deadlocks. Various deadlock prevention policies have been proposed to address this issue. Despite these efforts, resolving system deadlocks while achieving the optimal number of reachable states remains challenging. Based on existing research, we have developed a novel deadlock recovery method applicable to various flexible manufacturing systems. We designed an adaptable system and a controller that can restore the system to its fully operational state.

1. Introduction

System deadlocks are caused repeatedly in flexible manufacturing systems (FMSs) [1,2], resource allocation systems (RASs) [3,4], and automated manufacturing systems (AMSs) [5,6,7], so solving problems related to these deadlocks is a significant and urgent task. The Petri Net (PN) theory is the one most widely utilized for dealing with deadlock problems. In this study, we adopted reachability graph analysis as our main technique, which with structural analysis are the two main analyzing techniques in PN theory. Our deadlock recovery strategy has demonstrated permissiveness and an optimal performance. Unlike the traditional deadlock prevention strategy, our deadlock recovery strategy improves the system liveness of deadlock states rather than forbidding them. Lu et al. [8] developed a resource flow graph (RFG)-based deadlock recovery method to mitigate resource competition. This method features a low computation cost and an intuitive application, with no need to calculate the whole reachability graph. Tseng et al. [9] improved the RFG-based method to reduce the number of controllers and maintain the same performance.

We have developed an optimal deadlock recovery method to solve system deadlock problems. The existing RFG-based methods [8,9] built transition-based controllers that release the resources from all operations of the RFG and return them to idle and resource places. However, this method requires a lot of reallocating of whole resources. We rearranged the partial resources in the RFG to maintain permissiveness and reachability. An example of a system of simple sequential processes with resources(S³PR) net, modeled on the PN theory, was introduced for demonstration.

The rest of this article is laid out as follows: Section 2 provides an overview of the basic PN theory. Section 3 clarifies the central concept and the definition of an HRC. Section 4 introduces a classic PN model of S³PR net to demonstrate the proposed method and compare it with existing works. The final section gives a summary and our conclusions.

2. Preliminaries

According to basic PN theory [10], the PN model of S³PR net is a four-tuple $N=(P,T,F,W)$. A PN is illustrated as a directed bipartite graph, which is also called a Place/Transition net. $P$ and $T$ are two nonempty disjoint finite sets of places and transitions, respectively, where $P\cap T=\mathrm{\varnothing }$ and $P\cup T\ne \mathrm{\varnothing }$. $F$ denotes the set of arcs connecting places and transitions, such that $F\subseteq \left(P\times T\right)\cup (T\times P)$. $W:F\to {\mathbb{N}}^{+}$ is the weighted value of each arc in $F$. Each place of $N$ is marked with one or more tokens at the current time to represent its property. A marking (or state) is a one-dimensional array mapping $M:P\to \mathbb{Z}$ and $M_0$ is the initial marking of $N$. $M\left(p\right)$ denotes the marking of any place $p\in P$ within $M$.

Identical to graph theory, ${}^{•}x$ and $x^{•}$ indicate the pre- and post-set of the node $x$ of a PN model, no matter whether $x$ is a place or transition. Given a transition $t\in T$ for firing at marking $M$, $\forall p\in {}^{•}t:M\left(p\right)\ge W(p,t)$, which is also denoted as $M[t⟩$. $\neg M[t⟩$ means $t$ is disabled for the firing at marking $M$. An S³PR net contains idle, operation, and resource places, which are denoted as $P^0$, $P_A$, and $P_R$. Each sequential process of an S³PR consists of one idle place and certain operation places, and different processes are connected by various shared resources.

Definition 1.

Let $N=(P^0\cup P_A\cup P_R, T, F, W, M_0)$ be an S³PR net which holds the following:

(1) 

$P_A$ is the set of operation places, $\forall p_a\in P_A$, $M_0\left(p_a\right)=0$.

(2) 

$P_R$ is the set of resource places, $\forall p_r\in P_R, {}_{ }{}^{•}{p}_r\cap p_r^{ •}=\varnothing$; $\forall p_a\in P_A, t_i\in {}_{ }{}^{•}{p}_a, t_j\in p_a^{ •}, \exists p_r\in P_R, {}_{ }{}^{•}{t}_i\cap P_R=t_j^{ •}\cap P_R=\left\{p_r\right\}$; $\forall p_r\in P_R, {}_{ }{}^{••}{p}_r\cap P_A=p_r^{ ••}\cap P_A\ne \varnothing$.

(3) 

$P^0$ is the set of idle places and each sequential process contains one idle place $p^0$.

Using reachability graph analysis, all markings that were reachable from the initial one were found for further study. A reachability graph consists of nodes, which are labeled as markings, and arrows, labeled with transitions. $R(N,M_0)$ denotes the reachability graph of the PN model $N$ with the initial marking $M_0$. $\mathfrak{M}$ indicates the set of all markings, including $M_0$. A reachable marking $M$ can be reached by firing a sequence of transitions $\sigma =t_1{t}_2{t}_3\dots t_{n-1}{t}_n$, where $M_0[\sigma ⟩M$. A deadlock marking $M_D$ does not reach any other ones due to all transitions being disabled. To develop an optimal deadlock recovery solution, we used a control transition instead of a control place to deal with the deadlock problem. A control transition is a generated transition that is enabled at certain deadlock markings.

3. Hold and Request Circuit-Based Deadlock Recovery Policy

In this study, we built an optimal deadlock recovery method to provide maximum permissiveness and system liveness. A structure named a hold and request circuit (HRC) was used to enhance efficiency.

3.1. HRC

In S³PR systems, multiple production processes usually request shared resources to follow the steps of production. When any resource is held by one of the relevant processes while it waits for other resources, the others cannot obtain this resource again. System deadlocks caused by a lack of shared resources are undesirable and require full recovery. Via the specific subnet HRC, the flow between the resources and operation is checked, and then a set of well-designed control transitions is added to the system to reallocate those held resources.

An HRC contains operation and resource places, with connecting arrows between them used to present the flow relationships of the competing resources. As aforementioned, a deadlock occurs when resources are held by certain processes and these processes are waiting for other resources to carry out their next operation. When partial operation places and resource places are at a standstill and keep waiting, circular holding and waiting occur, which is one of the conditions of a deadlock. It is necessary to check all HRCs and build corresponding control transitions.

Definition 2.

Given an S³PR net $N=(P^0\cup P_A\cup P_R, T, F, W, M_0)$, a valid HRC ${\mathbb{G}}_{HRC}(\mathcal{V},\mathcal{U})$ holds:

(1) 

$\mathcal{V}$ is the set of nodes in the HRC, including operation places ${\mathcal{V}}_A\subseteq P_A$ and resource places ${\mathcal{V}}_R\subseteq P_R$, such that $\mathcal{V}={\mathcal{V}}_A\cup {\mathcal{V}}_R$.

(2) 

$\mathcal{U}$ is the set of edges in the HRC, implying a flow of circular holding and waiting. There are two types of resource flow: requesting resources and releasing them from operation, where $\mathcal{U}=\left\{v_a\to v_r \right| \exists t\in T, \left(v_r, t\right)\cup \left(t, v_a\right)\subseteq F\}\cup \{v_a\to v_r | \exists t\in T, \left(v_r, t\right)\cup \left(v_a, t\right)\subseteq F\}$.

(3) 

Given an HRC with ${\mathcal{V}}_A={\bigcup }_{i\in {\mathbb{N}}^{+}}^n{v}_{a_i}$ and ${\mathcal{V}}_R={\bigcup }_{i\in {\mathbb{N}}^{+}}^n{v}_{r_i}$, $\forall v_a\in {\mathcal{V}}_A, v_r\in {\mathcal{V}}_R, {}_{ }{}^{•}{v}_a\cup v_a^{ •}\subseteq {\mathcal{V}}_R, {}_{ }{}^{•}{v}_r\cup v_r^{ •}\subseteq {\mathcal{V}}_A$.

(4) 

It is noteworthy that there is no repetition of any node in each HRC.

3.2. Control Transition

Each valid HRC can form one corresponding control transition by reallocating resources. According to the concept of circular holding and waiting, the products and resources from idle and resource places are held in operation places. Therefore, control transitions are designed to solve these standstill conditions, release the products and the resources from operation places, and send them to idle places and resource places.

Definition 3.

Given an HRC ${\mathbb{G}}_{HRC}(\mathcal{V},\mathcal{U})$, its corresponding control transition $t_c$ has input arcs from all $v_a\in {\mathcal{V}}_A$, output arcs into all of $v_r\in {\mathcal{V}}_R$, and an idle place $p^0\in P^0$ belonging to the same process as $v_a$.

3.3. Efficiency Enhancement

In the HRC-based deadlock recovery method, all valid HRCs of the system are found, and related control transitions are generated. All the operation places and resource places of the HRCs are considered within obtaining solutions, but they also bring the requirement of higher consumption for the rearrangement of resources. We assume that not all nodes of the HRCs are necessary for developing solutions. An S³PR net contains two or more sequential processes with shared resources, with each process being a circuit of one idle place and one operation place. Each pair of operation places from the same HRC belongs to the same process, i.e., they share the same idle place $p^0$. In a deadlock marking, all operation places in the HRC cannot progress any further. Given two operation places $v_a^1$ and $v_a^2$ belong to the same HRC and share the same idle place $p^0$, the resources in $v_a^1$ and $v_a^2$ are not sent to the next operation place in this production circuit. As $v_a^1$ is closer to the end of this process than $v_a^2$, it releases its resources to partially recover the processing sequence. That is to say, in any sequential process, only one operation place needs to be considered when generating a control transition.

4. Experimental Results

A classic example of S³PR net was used for the demonstration of our proposed HRC-based method.

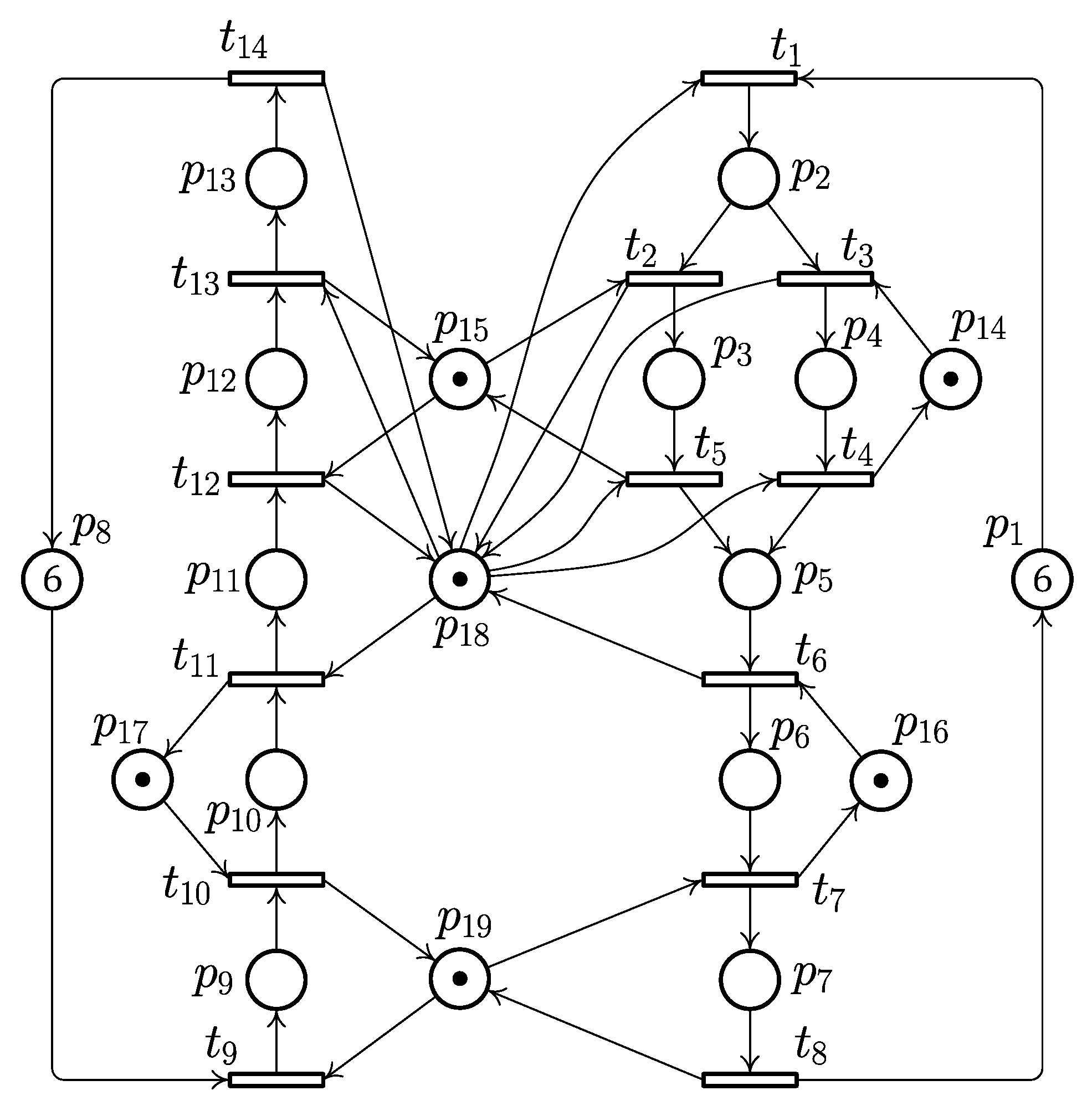
Example 1.

Considering the PN model in Figure 1, there are 19 places and 14 transitions in total, where $P^0=\{p_1,p_8\}$, $P_A=\left\{p_2,p_3,p_4,p_5,p_6,p_7,p_9,p_{10},p_{11},p_{12},p_{13}\right\},$ and $P_R=\{p_{14},p_{15},p_{16},p_{17},p_{18},p_{19}\}$. The initial marking $M_0=6p_1+6p_8+p_{14}+p_{15}+p_{16}+p_{17}+p_{18}+p_{19}$.

According to HRC-based deadlock recovery policies [8,9], there are four HRCs in Example 1. Their contents are shown in

Table 1. Contents of all HRCs.

HRC	${\mathcal{V}}_{\mathit{A}}$	${\mathcal{V}}_{\mathit{R}}$	$\mathcal{U}$
${\mathbb{G}}_{HR{C}_1}$	$p_2,p_4$	$p_{14},p_{18}$	$p_2\to p_{14},{p_{14}\to p}_4,p_4\to p_{18},p_{18}\to p_2$
${\mathbb{G}}_{HR{C}_2}$	$p_3,p_{11}$	$p_{15},p_{18}$	$p_{11}\to p_{15},p_{15}\to p_3,p_3\to p_{18},p_{18}\to p_{11}$
${\mathbb{G}}_{HR{C}_3}$	$p_{11},p_{12}$	$p_{15},p_{18}$	$p_{11}\to p_{15},p_{15}\to p_{12},p_{12}\to p_{18},p_{18}\to p_{11}$
${\mathbb{G}}_{HR{C}_4}$	$p_5,p_6,p_9,p_{10}$	$p_{16},p_{17},p_{18},p_{19}$	$p_{18}\to p_5,p_5\to p_{16},p_{16}\to p_6,p_6\to p_{19},$ $p_{19}\to p_9,p_9\to p_{17},p_{17}\to p_{10},p_{10}\to p_{18}$

.

There are two sequential processes in the net in Figure 1, including $p_1{t}_1{p}_2{t}_2{p}_3{t}_5\left(t_3{p}_4{t}_4\right)p_5{t}_6{p}_6{t}_7{p}_7{t}_8$ and $p_8{t}_9{p}_9{t}_{10}{p}_{10}{t}_{11}{p}_{11}{t}_{12}{p}_{12}{t}_{13}{p}_{13}{t}_{14}$. Only ${\mathbb{G}}_{HR{C}_4}$ has more than one operation place belonging to each sequential process; the other HRCs have one operation place each. According to Section III-C, ${\mathbb{G}}_{HR{C}_4}$ can be replaced by ${\mathbb{G}}_{HR{C}_4}^{\star }=({\mathcal{V}}_4^{\star },{\mathcal{U}}_4^{\star })$ when ${\mathcal{V}}_4^{\star }=\{p_6,p_{10},p_{16},p_{17}\}$. The newly generated control transitions are shown in

Table 2. Generated control transitions.

${\mathit{t}}_{{\mathit{c}}_{\mathit{i}}}$	${}^{•}{\mathit{t}}_{{\mathit{c}}_{\mathit{i}}}$	${\mathit{t}}_{{\mathit{c}}_{\mathit{i}}}^{•}\cap {\mathit{P}}_{\mathit{R}}$	${\mathit{t}}_{{\mathit{c}}_{\mathit{i}}}^{•}\cap {\mathit{P}}^0$
$t_{c_1}$	$p_2,p_4$	$p_{14},p_{18}$	$2p_1$
$t_{c_2}$	$p_3,p_{11}$	$p_{15},p_{18}$	$p_1,p_8$
$t_{c_3}$	$p_{11},p_{12}$	$p_{15},p_{18}$	$2p_8$
$t_{c_4}$	$p_6,p_{10}$	$p_{16},p_{17}$	$p_1,p_8$

.

After four control transitions $t_{c_1},t_{c_2},t_{c_3},t_{c_4}$ are added to the original net in Figure 1, the controlled net is checked with no any reachable deadlock marking by simulation software. The comparative results of the HRC-based methods are shown in

Table 3. Comparison of all RFG-based methods.

Methods	$\left|\mathfrak{M}\right|$	$\left|{\mathit{T}}_{\mathit{c}}\right|$	$|{}^{•}{\mathit{T}}_{\mathit{c}}\cup {\mathit{T}}_{\mathit{c}}^{•}|$	Liveness
[8]	282	6	42	Deadlock-free
[9]	282	4	30	Deadlock-free
Proposed	282	4	24	Deadlock-free

, where the proposed method provides a better performance.

5. Conclusions

We developed an HRC-based deadlock recovery policy that led to an improvement in performance and efficiency. The experimental and comparative results showed that the proposed method is better than other HRC-based ones. In future research, it will be necessary to consider a more complicated system and enhance that system’s performance.