A Quantitative Model of Supply Chain Disruption Propagation Dynamics †
Abstract
1. Introduction
2. Literature Review
3. Problem Formulation
4. Modeling Process and Material Flow
5. Characteristics of Disruption Propagation
5.1. Disruption Signal Generation and Profile
5.2. Disruption Propagation Across One Tier
5.3. Disruption Propagation Along Multiple Tiers
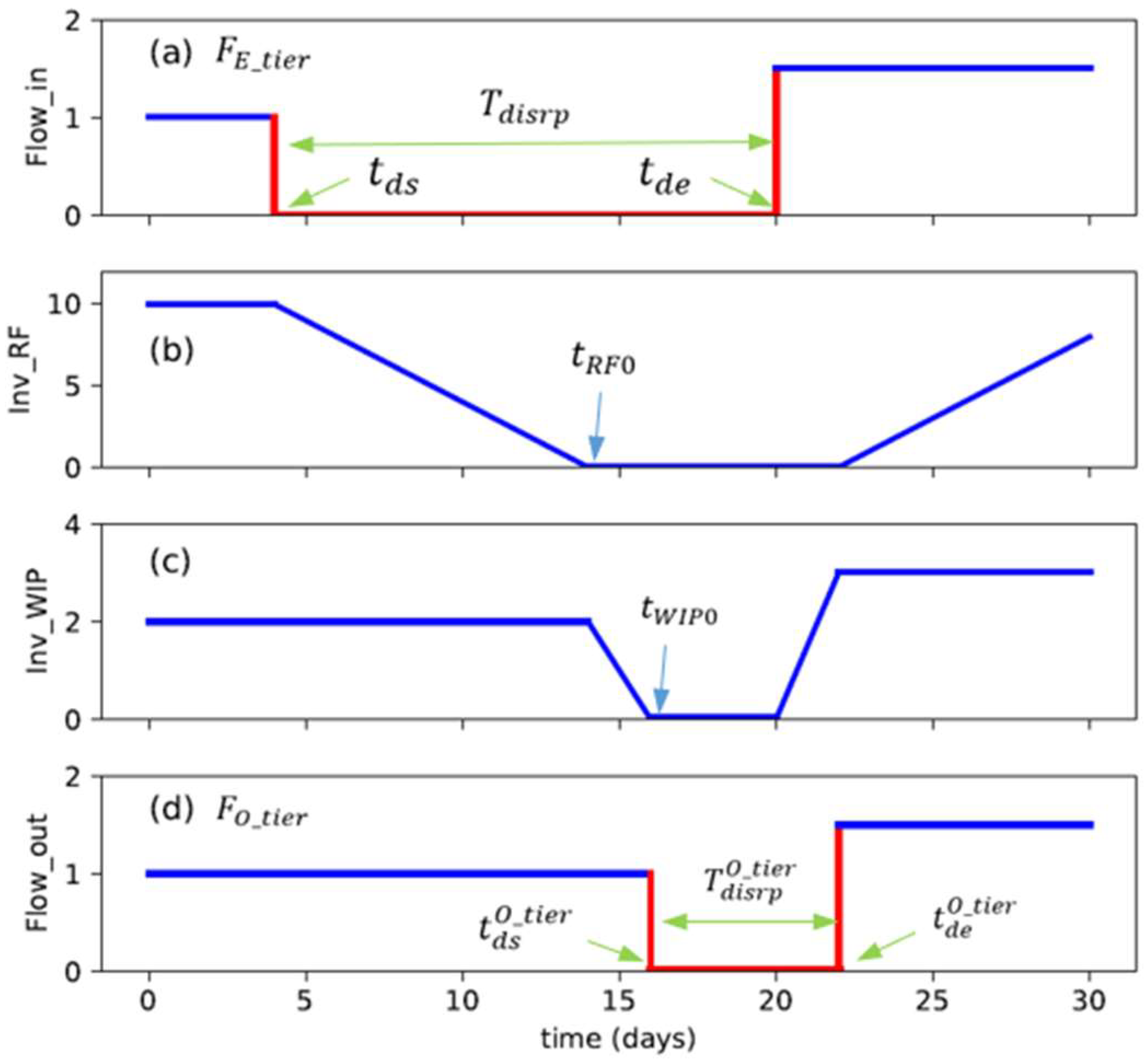
- Inventory is critical in preventing disruption propagation, and it can work as a buffer to reduce the effect of input flow disruption. It is the inventory of raw materials and final products that plays a critical role. When a disruption propagates through a tier, the duration of disruption is reduced by their combined inventory level (in terms of the time unit). The WIP can delay the start time of disruption for the next tiers, but it does not affect the duration of disruption.
- The number of tiers that a material flow disruption propagates depends on the sum of inventories of raw material and final product at different tiers from the source of the disruption. As the disruption propagates, it becomes weaker and eventually ceases at the entry point of a certain tier. Therefore, from a focal company’s perspective, it is often unnecessary to look into many tiers upstream.
- For the MTO supplier of a focal company, its disruptions are more likely to propagate to the focal company than those from MTS suppliers. This is because the MTO supplier has no final product inventory and, thus, typically has less total inventory than MTS suppliers. Therefore, when we develop a monitoring system for disruption, if many upstream tiers are of MTO tiers, we may need to monitor more upstream tiers compared to the case in which many upstream tiers are of MTS tiers.
- From the mechanism of disruption propagation, we can estimate the scale of disruption that should be monitored at each tier and establish appropriate thresholds. Based on the formula of propagation, we can derive which scale (threshold) of disruption at each tier will be able to propagate to the focal company. Therefore, if the disruption happening at a given tier is less than its corresponding threshold, the focal company does not need to monitor this disruption. The larger the tier number of suppliers, the larger the threshold. This is useful for developing an effective disruption monitoring system. Nevertheless, in setting such thresholds, other factors, such as the uncertainties, must be considered in upstream parameter estimations and the risk level that the focal company can afford.
- The time is estimated when a disruption at a certain upstream tier is propagated to the focal company. From this time, the focal company knows how much time it has to adopt mitigation plans or implement response measures.
5.4. Stochastic Parameters
6. Numerical Example
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qin, R.; Khakzad, N.; Zhu, J. An overview of the impact of hurricane harvey on chemical and process facilities in Texas. Int. J. Disaster Risk Reduct. 2020, 45, 101453. [Google Scholar] [CrossRef]
- Sokolov, B.; Ivanov, D.; Dolgui, A. The ripple effect in supply chains: Trade of efficiency-flexibility-resilience in disruption management. Int. J. Prod. Res. 2014, 52, 2154–2172. [Google Scholar]
- Hosseini, S.; Ivanov, D. Bayesian networks for supply chain risk, resilience and ripple effect analysis: A literature review. Expert Syst. Appl. 2020, 161, 113649. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Ivanov, D.; Dolgui, A. Ripple effect modelling of supplier disruption: Integrated Markov chain and dynamic Bayesian network approach. Int. J. Prod. Res. 2020, 58, 3284–3303. [Google Scholar] [CrossRef]
- Ivanov, D.A.; Dolgui, A.; Sokolov, B.V.; Ivanov, M. Literature review on disruption recovery in the supply chain. Int. J. Prod. Res. 2017, 55, 6158–6174. [Google Scholar] [CrossRef]
- Rinaldi, M.; Murino, T.; Gebennini, E.; Morea, D.; Bottani, E. A literature review on quantitative models for supply chain risk management: Can they be applied to pandemic disruptions? Comput. Ind. Eng. 2022, 170, 108329. [Google Scholar] [CrossRef] [PubMed]
- Katsaliaki, K.; Galetsi, P.; Kumar, S. Supply chain disruptions and resilience: A major review and future research agenda. Ann. Oper. Res. 2022, 319, 965–1002. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zeng, A.Z.; Zhao, L. Single or dual sourcing: Decision-making in the presence of supply chain disruption risks. Omega 2009, 37, 788–800. [Google Scholar] [CrossRef]
- Xu, H.-Y.; Fu, X.; Ponnambalam, L.; Namatame, A.; Yin, X.F.; Goh, R.S.M. A model to evaluate risk propagation considering effect of dynamic risk information sharing and multi-sourcing in supply chain networks. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 6–9 December 2015; pp. 1593–1597. [Google Scholar]
- Wilson, M.C. The impact of transportation disruptions on supply chain performance. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 295–320. [Google Scholar] [CrossRef]
- Schmitt, A.J.; Singh, M. A quantitative analysis of disruption risk in a multi-echelon supply chain. Int. J. Prod. Econ. 2012, 139, 22–32. [Google Scholar] [CrossRef]
- Tan, P.S.; Lee, S.G.; Tan, C.S. Modeling disruption propagation in a complex supply chain. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; pp. 154–158. [Google Scholar]
- Liu, R.; Kumar, A.; van der Aalst, W. A formal modeling approach for supply chain event management. Decis. Support Syst. 2007, 43, 761–778. [Google Scholar] [CrossRef]
- Blackhurst, J.; Wu, T.; Ogrady, P. Methodology for supply chain disruption analysis. Int. J. Prod. Res. 2007, 45, 1665–1682. [Google Scholar]
- Zegordi, S.H.; Davarzani, H. Developing a supply chain disruption analysis model: Application of colored petri-nets. Expert Syst. Appl. 2012, 39, 2102–2111. [Google Scholar] [CrossRef]
- Liu, S.; Song, M.; Tan, K.C.; Zhang, C. Multiclass dynamic inventory rationing with stochastic demands and backordering. Eur. J. Oper. Res. 2015, 244, 153–163. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, C. An efficient inventory rationing strategy for systems with two demand classes and backordering. Int. J. Prod. Res. 2015, 53, 6136–6142. [Google Scholar] [CrossRef]
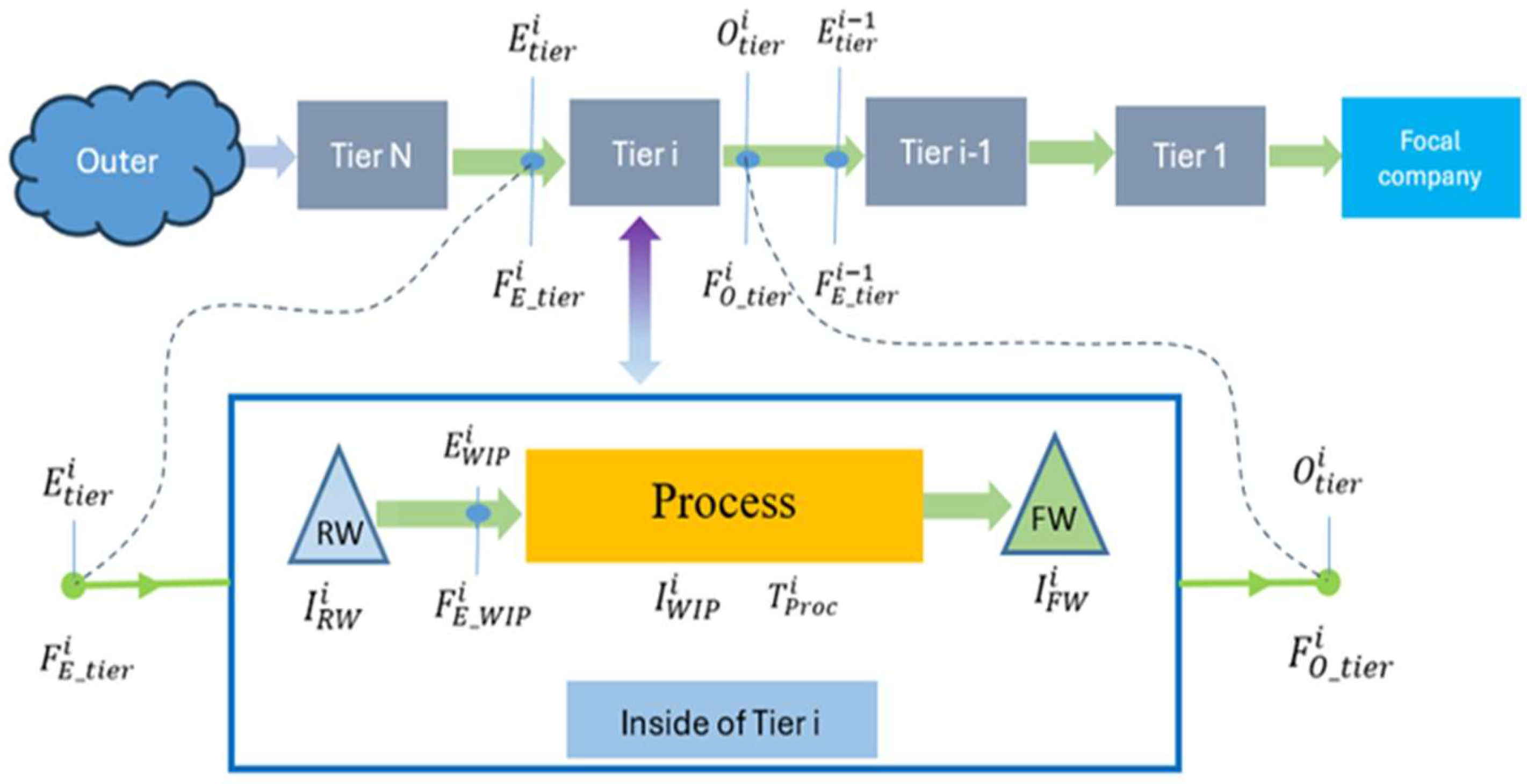
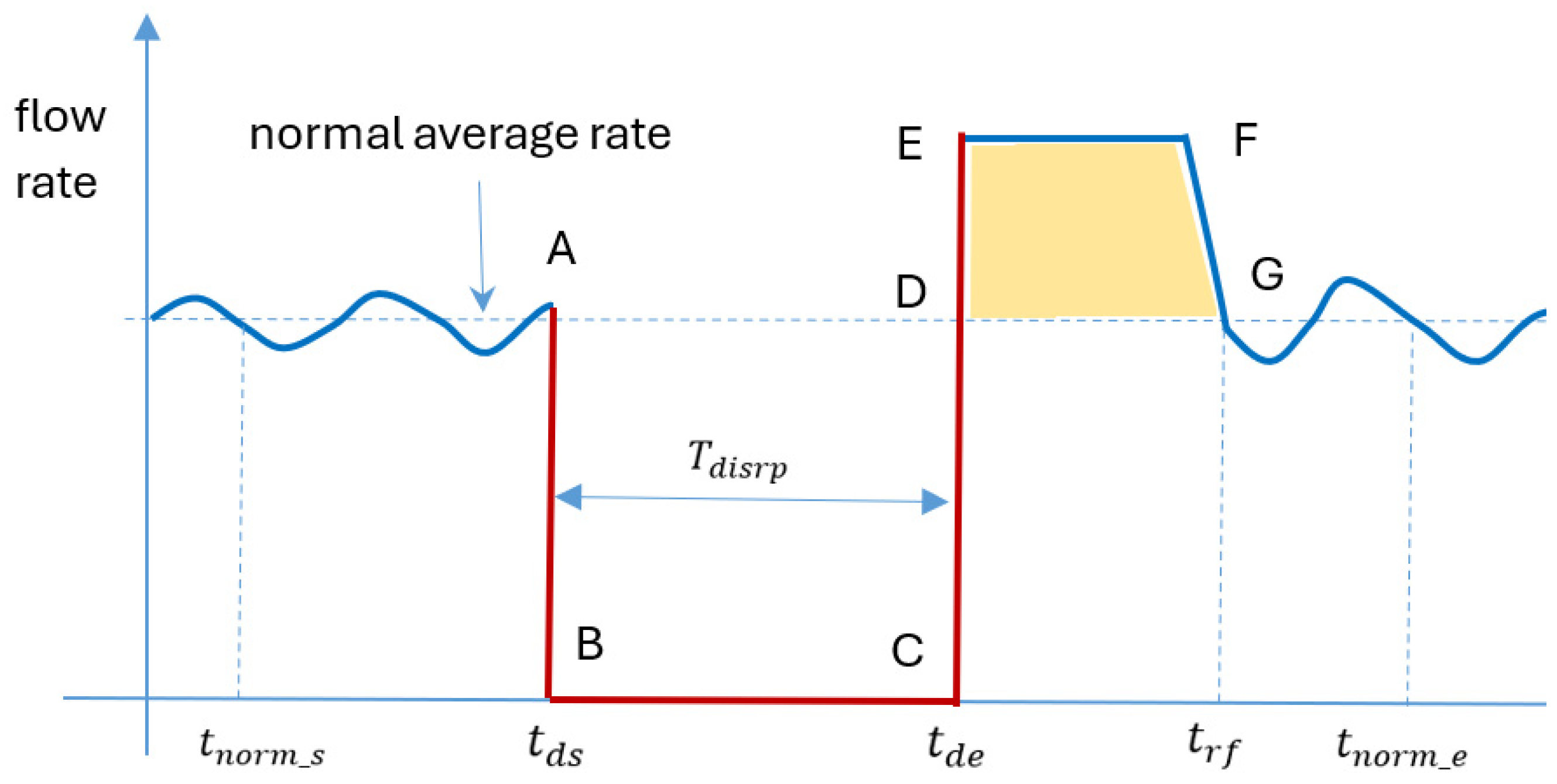
| Symbol | Meaning |
|---|---|
| material flow entry point (location) and output point (location) of tier i, respectively | |
| material flow rate entering and leaving tier i, respectively | |
| inventory level for raw material, final product, and work in progress, respectively | |
| process time converting raw material into products | |
| total inventory of raw material and final product at tier i | |
| transportation time between tiers i and i − 1 | |
| duration of disruption |
| Tier | ||||||
|---|---|---|---|---|---|---|
| K | 15 | 5 | 4 | 0 | 30 | 30 |
| K − 1 | 18 | 6 | 2 | 24 | 39 | 15 |
| K − 2 | 10 | 3 | 2 | --- | --- | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Xiang, S.; Wang, L. A Quantitative Model of Supply Chain Disruption Propagation Dynamics. Eng. Proc. 2025, 89, 1. https://doi.org/10.3390/engproc2025089001
Liu S, Xiang S, Wang L. A Quantitative Model of Supply Chain Disruption Propagation Dynamics. Engineering Proceedings. 2025; 89(1):1. https://doi.org/10.3390/engproc2025089001
Chicago/Turabian StyleLiu, Shudong, Shili Xiang, and Lu Wang. 2025. "A Quantitative Model of Supply Chain Disruption Propagation Dynamics" Engineering Proceedings 89, no. 1: 1. https://doi.org/10.3390/engproc2025089001
APA StyleLiu, S., Xiang, S., & Wang, L. (2025). A Quantitative Model of Supply Chain Disruption Propagation Dynamics. Engineering Proceedings, 89(1), 1. https://doi.org/10.3390/engproc2025089001






