Performance Monitoring for Galileo High Accuracy Service and Reliable Galileo Service Operations †
Abstract
1. Introduction
2. Galileo Services and HAS
- Collecting Galileo HAS corrections as well as raw GNSS ranging measurements globally at the GSS as part of continuous 24/7 operations.
- Obtaining the most recent reference dataset for the routine comparison and quality monitoring of the Galileo HAS corrections.
- Generating PPP solution(s) with an EU-approved HAS user algorithm (HAS-UA) (see [3], pg. 38 and Appendix E) with multiple signal/frequency/constellation combinations routinely (with daily restarts) using Galileo HAS-generated precise GNSS products and the collected GSS raw measurements. This allows the monitoring (identification and isolation) of any potential anomalies on the receiver side or the broadcast HAS corrections themselves.
- Computing the Galileo HAS correction availability at the average and worst user location (AUL/WUL) in the globe.
3. Service Operations for Galileo HAS
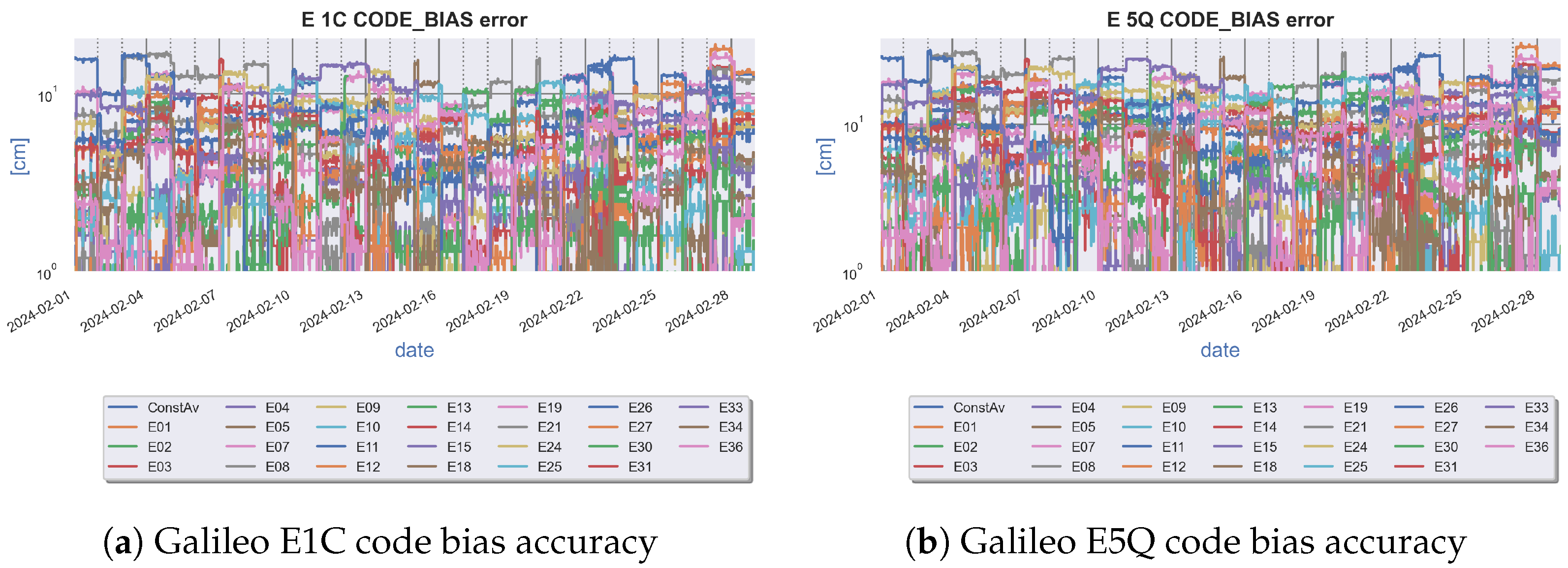
3.1. Galileo HAS Correction Accuracy
- 1.
- In the first step, the HAS corrections are decoded from the GSS E6B binary data and consolidated.
- 2.
- 3.
- In a second step these intermediate products (from Step 1 above) are subtracted from the corresponding reference values (3) after applying the appropriate coordinate transformations (see [9], pg. 41 and §7.2 for orbit correction and pg. 42 and §7.3 for clock correction) to ensure consistency. These are summarized in Equations (5a) and (6a) for orbit and clock, respectively. Although not explicitly described in this paper, a similar procedure is used to evaluate the code bias accuracy.
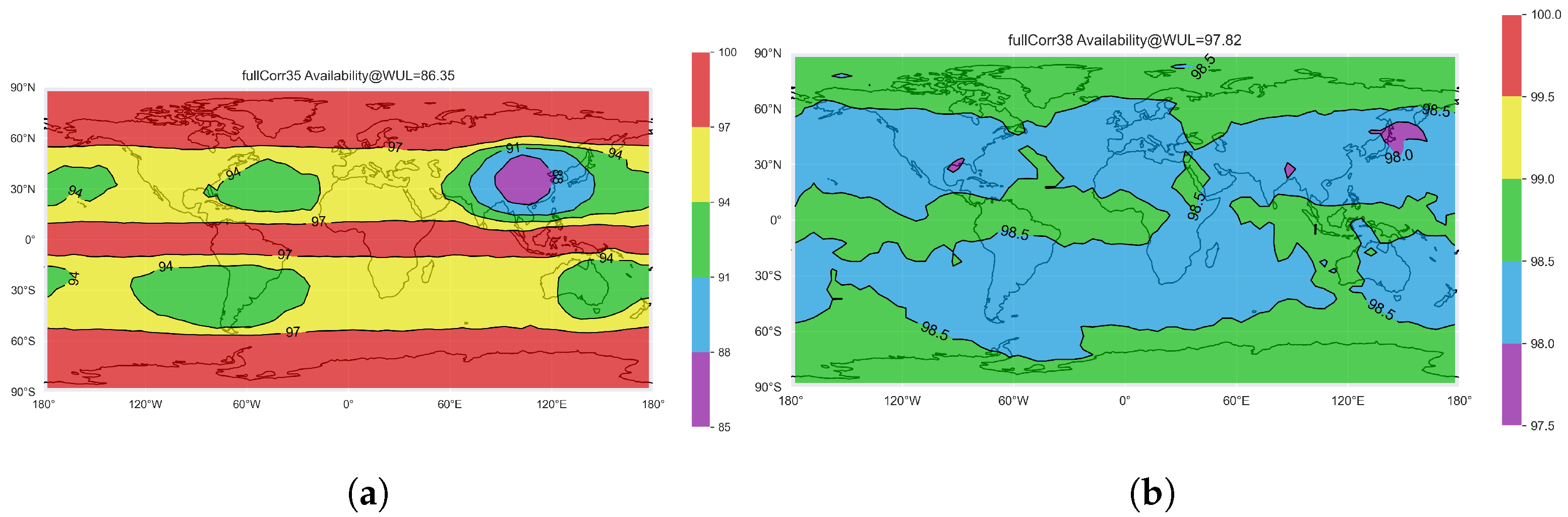
3.2. Galileo HAS Correction Availability
3.3. Galileo HAS Typical Positioning Accuracy
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EU. Galileo Open Service Signal-in-Space Interface Control Document; Galileo OS SIS ICD; European Union Agency for the Space Programme (EUSPA): Prague, Czech Republic, 2023. [Google Scholar]
- EU. Galileo High Accuracy Service Signal-in-Space Interface Control Document; Galileo HAS SIS ICD; European Union Agency for the Space Programme (EUSPA): Prague, Czech Republic, 2022. [Google Scholar]
- EU. Galileo High Accuracy Service definition doccument (HAS SDD); Galileo HAS SDD; European Union Agency for the Space Programme (EUSPA): Prague, Czech Republic, 2023. [Google Scholar]
- Springer, T.; Hugentobler, U. IGS ultra rapid products for (near-) real-time applications. Phys. Chem. Earth Part A: Solid Earth Geod. 2001, 26, 623–628. [Google Scholar] [CrossRef]
- IGS. International GNSS Service Real-Time Service (IGS RTS). Available online: https://igs.org/rts/ (accessed on 18 August 2025).
- Dach, R.; Bockmann, E. International GNSS Service Technical Report 2022 (IGS Annual Report). IGS Central Bureau and University of Bern; Bern Open Publishing, 2023. Available online: https://doi.org/10.48350/179297 (accessed on 18 August 2025).
- Weber, G.; Dettmering, D.; Gebhard, H. Networked transport of RTCM via internet protocol (NTRIP). In A Window on the Future of Geodesy: Proceedings of the International Association of Geodesy IAG General Assembly, Sapporo, Japan, 30 June–11 July 2003; Springer: Berlin/Heidelberg, Germany, 2005; pp. 60–64. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Multi-GNSS signal-in-space range error assessment–Methodology and results. Adv. Space Res. 2018, 61, 3020–3038. [Google Scholar] [CrossRef]
- EU. Galileo High Accuracy Service Service Definition Document (HAS SDD); European Union: Prague, Czech Republic, 2022. [Google Scholar] [CrossRef]
- de Blas, F.; Vázquez, J.; Hernández, C.; Ostolaza, J.; Lagrasta, S.; Fernandez-Hernández, I.; Blonski, D. The Galileo High Accuracy Service (HAS): A Pioneer Free-of-Charge Global Precise Positioning Service. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 449–468. [Google Scholar]
- Naciri, N.; Yi, D.; Bisnath, S.; de Blas, F.J.; Capua, R. Assessment of Galileo High Accuracy Service (HAS) test signals and preliminary positioning performance. GPS Solut. 2023, 27, 73. [Google Scholar] [CrossRef] [PubMed]
- Martini, I.; Susi, M.; Cucchi, L.; Fernandez-Hernandez, I. Galileo high accuracy service performance and anomaly mitigation capabilities. Gps Solut. 2024, 28, 25. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O.; Steigenberger, P.; Martini, I.; Fernandez-Hernandez, I. Orbit determination of Sentinel-6A using the Galileo high accuracy service test signal. Gps Solut. 2022, 26, 120. [Google Scholar] [CrossRef]
- EU. Galileo Services—High Accuracy Service Performance Report 2023; European Union Agency for the Space Programme (EUSPA): Prague, Czech Republic, 2023. [Google Scholar]
- Fernandez-Hernandez, I.; Chamorro-Moreno, A.; Cancela-Diaz, S.; Calle-Calle, J.D.; Zoccarato, P.; Blonski, D.; Senni, T.; de Blas, F.J.; Hernández, C.; Simón, J.; et al. Galileo high accuracy service: Initial definition and performance. Gps Solut. 2022, 26, 65. [Google Scholar] [CrossRef]
- Galileo authentication and high accuracy: Getting to the truth. Available online: https://insidegnss.com/galileo-authentication-and-high-accuracy-getting-to-the-truth/ (accessed on 18 August 2025).
- Cucchi, L.; Damy, S.; Gioia, C.; Motella, B.; Paonni, M. Testing the Galileo High Accuracy Service in Different Operational Scenarios. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 2712–2722. [Google Scholar]
- GPS Directorate. NAVSTAR GPS Space Segment/Navigation User Interfaces. Interface Specification IS-GPS-200, Revision M; El Segundo, CA, USA, May 2021. Available online: https://apps.dtic.mil/sti/pdfs/ADA255994.pdf (accessed on 18 August 2025).
- Gendt, G.; Altamimi, Z.; Dach, R.; Söhne, W.; Springer, T.; The GGSP Prototype Team. GGSP: Realisation and maintenance of the Galileo terrestrial reference frame. Adv. Space Res. 2011, 47, 174–185. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A. Code Biases in Multi-GNSS Point Positioning. In Proceedings of the 2013 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 28–30 January 2013. [Google Scholar]
- Susi, M.; Borio, D.; Azeez, A.; Park, J.; Wezka, K.; Fernandez-Hernandez, I. Assessing the High-Accuracy Service at High Latitudes. Eng. Proc. 2023, 54, 8. [Google Scholar]


| Month | GPS Orbit Correction (cm) | GPS Clock Correction (cm) | GPS Code Bias (C1C) (cm) | Galileo Orbit Correction (cm) | Galileo Clock Correction (cm) | Galileo Code Bias (C1C) (cm) |
|---|---|---|---|---|---|---|
| January 2024 | 16.4 | 10.1 | 25.1 | 15.7 | 7.0 | 6.7 |
| February 2024 | 15.3 | 10.0 | 20.7 | 15.9 | 7.3 | 7.9 |
| March 2024 | 18.3 | 10.0 | 17.5 | 17.7 | 8.1 | 9.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lalgudi Gopalakrishnan, G.; Salonico, A.; De Blas, J.; Carandente, V.; Pintor, P.; Nordmann, C. Performance Monitoring for Galileo High Accuracy Service and Reliable Galileo Service Operations. Eng. Proc. 2025, 88, 73. https://doi.org/10.3390/engproc2025088073
Lalgudi Gopalakrishnan G, Salonico A, De Blas J, Carandente V, Pintor P, Nordmann C. Performance Monitoring for Galileo High Accuracy Service and Reliable Galileo Service Operations. Engineering Proceedings. 2025; 88(1):73. https://doi.org/10.3390/engproc2025088073
Chicago/Turabian StyleLalgudi Gopalakrishnan, Ganesh, Antonio Salonico, Javier De Blas, Valerio Carandente, Pedro Pintor, and Chris Nordmann. 2025. "Performance Monitoring for Galileo High Accuracy Service and Reliable Galileo Service Operations" Engineering Proceedings 88, no. 1: 73. https://doi.org/10.3390/engproc2025088073
APA StyleLalgudi Gopalakrishnan, G., Salonico, A., De Blas, J., Carandente, V., Pintor, P., & Nordmann, C. (2025). Performance Monitoring for Galileo High Accuracy Service and Reliable Galileo Service Operations. Engineering Proceedings, 88(1), 73. https://doi.org/10.3390/engproc2025088073






