Multipath Characterization of GNSS Ground Stations Using RINEX Observations and Machine Learning †
Abstract
1. Introduction
2. Data Processing and Feature Computation
2.1. Data Pre-Processing
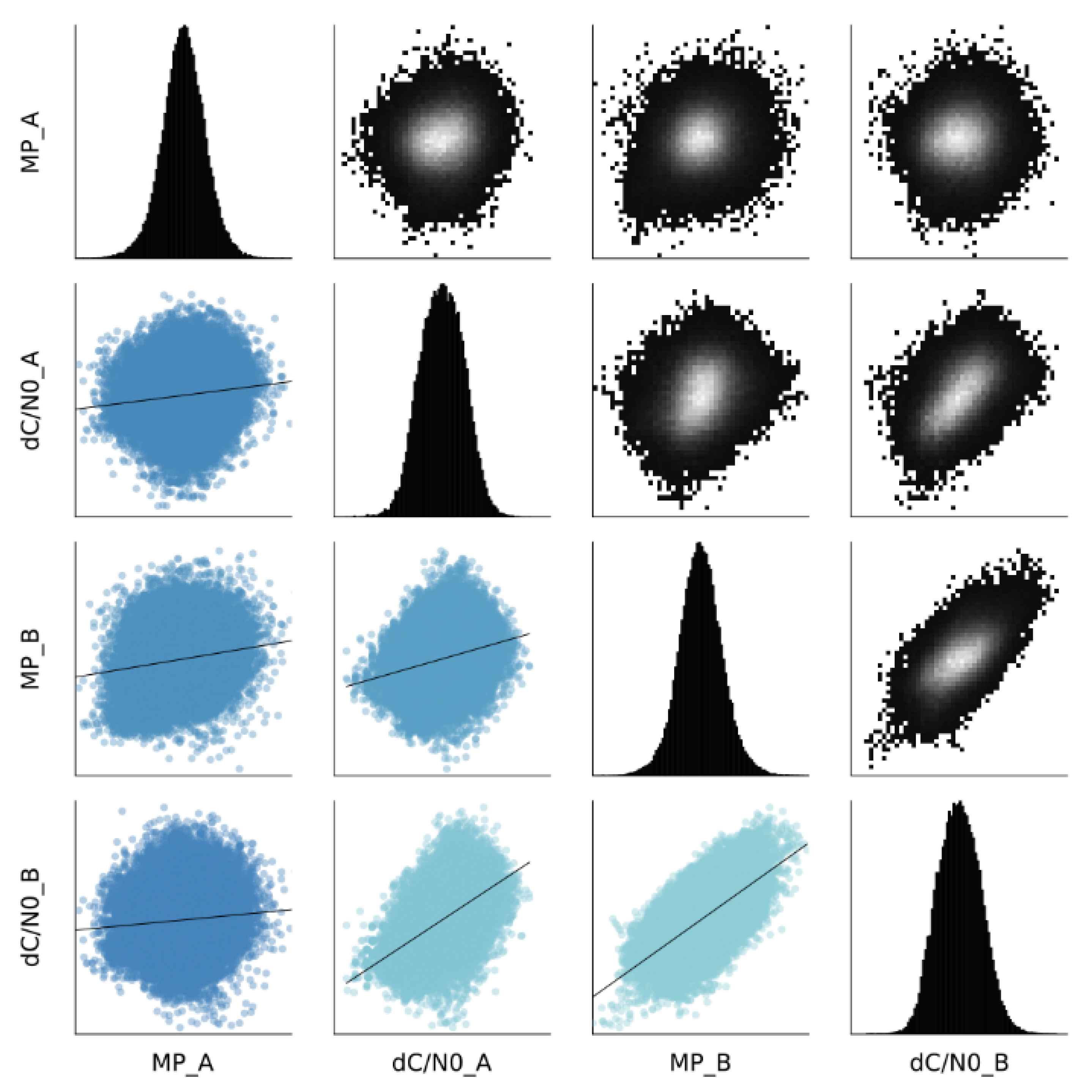
2.2. Feature Computation
3. Machine Learning Methods and Model Training
3.1. Training Data Selection
3.2. Machine Learning Methods
3.3. Model Training and Validation
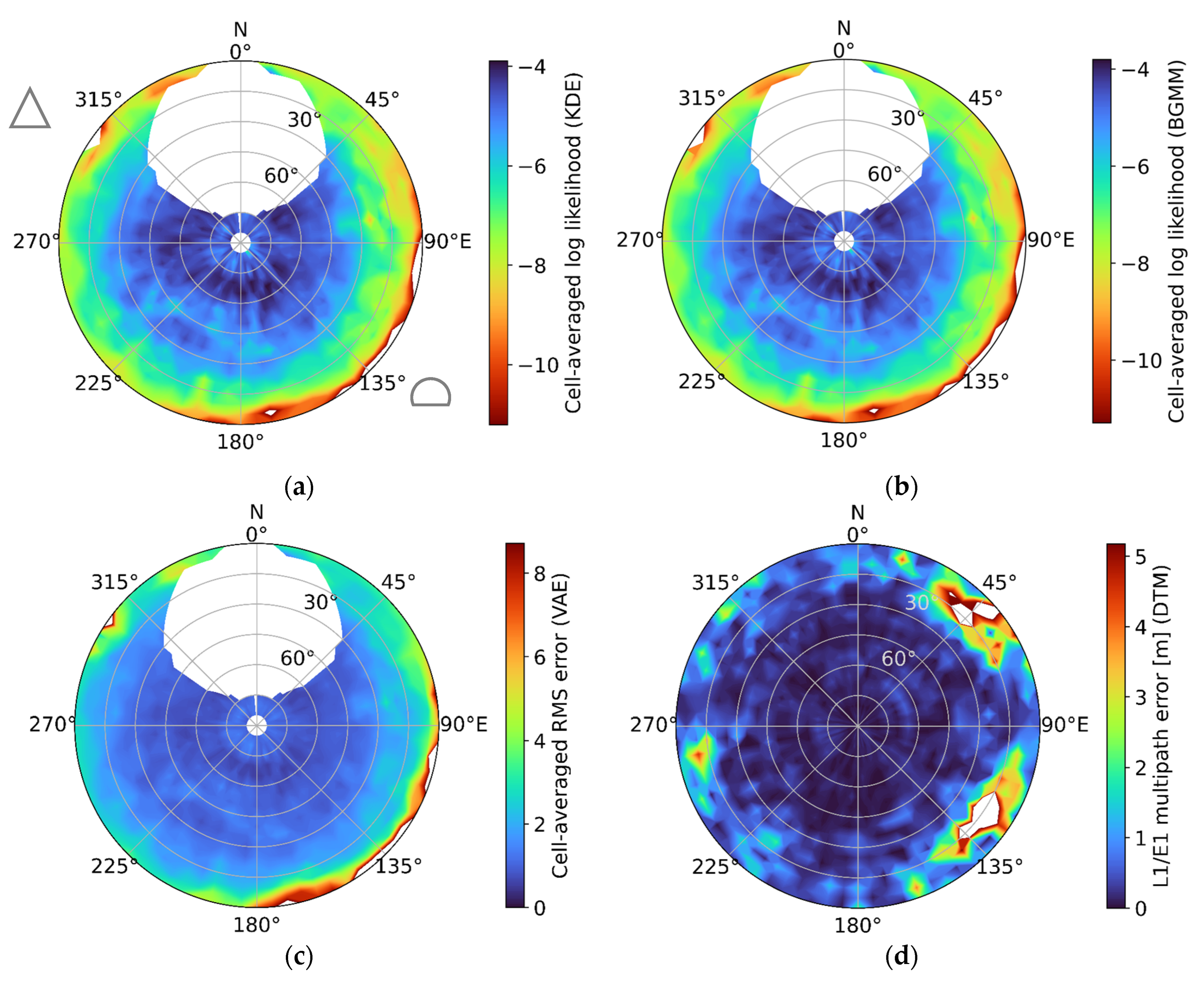
4. Multipath Characterization Using a Digital Twin Model
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bevly, D.; Martin, S. Navigation in advanced driver-assisted systems and automated driving. In Positioning, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Jade Morton, Y.T., van Diggelen, F., Spilker, J.J., Jr., Parkinson, B.W., Lo, S., Gao, G., Eds.; The IEEE, Inc.: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2021; Volume 2, pp. 1769–1810. [Google Scholar]
- Pullen, S.; Joerger, M. GNSS integrity and receiver autonomous integrity monitoring (RAIM). In Positioning, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Jade Morton, Y.T., van Diggelen, F., Spilker, J.J., Jr., Parkinson, B.W., Lo, S., Gao, G., Eds.; The IEEE, Inc.: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2021; Volume 1, pp. 591–617. [Google Scholar]
- Thoelert, S.; Circiu, M.-S.; Meurer, M. Impact of satellite biases on the position in differential MFMC applications. In Proceedings of the International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 21–24 January 2020; pp. 222–235. [Google Scholar] [CrossRef]
- Lee, J.; Jade Morton, Y.T.; Lee, J.; Moon, H.-S.; Seo, J. Monitoring and mitigation of ionospheric anomalies for GNSS-based safety critical systems: A review of up-to-date signal processing techniques. IEEE Sig. Proc. Mag. 2017, 34, 96–110. [Google Scholar] [CrossRef]
- Thombre, S.; Bhuiyan, M.Z.; Eliardsson, P.; Gabrielsson, B.; Pattinson, M.; Dumville, M.; Fryganiotis, D.; Hill, S.; Manikundalam, V.; Pölöskey, M.; et al. GNSS threat monitoring and reporting: Past, present, and a proposed future. J. Navig. 2018, 71, 513–529. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, J. Real-time monitoring for a wide area precise positioning system. Sat. Nav. 2020, 1, 24. [Google Scholar] [CrossRef]
- van Graas, F.; Ugazio, S. GNSS signal quality monitoring. In Positioning, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Jade Morton, Y.T., van Diggelen, F., Spilker, J.J., Jr., Parkinson, B.W., Lo, S., Gao, G., Eds.; The IEEE, Inc.: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2021; Volume 1, pp. 215–231. [Google Scholar]
- Walter, T. Satellite based augmentation systems. In Springer Handbook of Global Navigation Satellite System; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International: Berlin/Heidelberg, Germany, 2017; pp. 339–361. [Google Scholar]
- Hauschild, A. Combinations of observations. In Springer Handbook of Global Navigation Satellite System; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International: Berlin/Heidelberg, Germany, 2017; pp. 583–604. [Google Scholar]
- Braasch, M.S. Multipath. In Springer Handbook of Global Navigation Satellite System; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International: Berlin/Heidelberg, Germany, 2017; pp. 443–468. [Google Scholar]
- Maqsood, M.; Gao, S.; Montenbruck, O. Antennas. In Springer Handbook of Global Navigation Satellite System; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International: Berlin/Heidelberg, Germany, 2017; pp. 505–534. [Google Scholar]
- Caizzone, S.; Schöfeldt, M.; Elmarissi, W.; Circiu, M.S. Antennas as precise sensors for GNSS reference stations and high-performance PNT applications on Earth and in space. Sensors 2021, 21, 4192. [Google Scholar] [CrossRef] [PubMed]
- Azarbad, M.R.; Mosavi, M.R. A new method to mitigate multipath error in single-frequency GPS receiver with wavelet transform. GPS Sol. 2014, 18, 189–198. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X.; Zhang, C. Convolutional neural network based multipath detection method for static and kinematic GPS high precision positioning. Remote Sens. 2018, 10, 2052. [Google Scholar] [CrossRef]
- Hsu, L. GNSS multipath detection using a machine learning approach. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Suzuki, T.; Amano, Y. NLOS multipath classification of GNSS signal correlation output using machine learning. Sensors 2021, 21, 2503. [Google Scholar] [CrossRef] [PubMed]
- Romero, I. (Ed.) The Receiver Independent Exchange Format (RINEX) v4; IGS/RTCM RINEX WG Chair; ESA/ESOC/Navigation Support Office: Darmstadt, Germany, 2021. [Google Scholar]
- Pan, Y.; Möller, G.; Soja, B. Machine learning-based multipath modeling in spatial domain applied to GNSS short baseline processing. GPS Sol. 2024, 28, 9. [Google Scholar] [CrossRef]
- Groves, P.D.; Jian, Z.; Rudi, M.; Strode, P. A portfolio approach to NLOS and multipath mitigation in dense urban areas. In Proceedings of the International Technical Meeting of the Satellite Division of The Institute of Navigation, Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Zhang, Z.; Li, B.; Gao, Y.; Shen, Y. Real-time carrier phase multipath detection based on dual-frequency C/N0 data. GPS Sol. 2019, 23, 7. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Attias, H. A variational Bayesian framework for graphical models. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 29 November–4 December 1999; pp. 209–215. [Google Scholar]
- Blei, D.M.; Jordan, M.I. Variational inference for Dirichlet process mixtures. Bayes. Anal. 2006, 1, 121–143. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1987; pp. 318–362. [Google Scholar]
- Klingma, D.P.; Welling, M. Auto-enconding variational Bayes. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Addo, E.O.; Elmarissi, W.; Caizzone, S. Digital twin-enabled characterization of GNSS multipath in challenging reference stations using a dual-polarized probe. J. Inst. Navig. 2024, 71, navi.644. [Google Scholar] [CrossRef]
- Dassault-Systèmes. CST Studio Suite: Electromagnetic Field Simulation Software. Brochure. Available online: www.3ds.com/fileadmin/PRODUCTS-SERVICES/SIMULIA/PRODUCTS/CST/CST_Brochure_A4.pdf (accessed on 1 January 2022).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allende-Alba, G.; Caizzone, S.; Addo, E.O. Multipath Characterization of GNSS Ground Stations Using RINEX Observations and Machine Learning. Eng. Proc. 2025, 88, 72. https://doi.org/10.3390/engproc2025088072
Allende-Alba G, Caizzone S, Addo EO. Multipath Characterization of GNSS Ground Stations Using RINEX Observations and Machine Learning. Engineering Proceedings. 2025; 88(1):72. https://doi.org/10.3390/engproc2025088072
Chicago/Turabian StyleAllende-Alba, Gerardo, Stefano Caizzone, and Ernest Ofosu Addo. 2025. "Multipath Characterization of GNSS Ground Stations Using RINEX Observations and Machine Learning" Engineering Proceedings 88, no. 1: 72. https://doi.org/10.3390/engproc2025088072
APA StyleAllende-Alba, G., Caizzone, S., & Addo, E. O. (2025). Multipath Characterization of GNSS Ground Stations Using RINEX Observations and Machine Learning. Engineering Proceedings, 88(1), 72. https://doi.org/10.3390/engproc2025088072






