Integrity Monitoring of GNSS Constellations with Only LEO-PNT Satellites ^†

Abstract

This paper explores the usage of LEO-PNT (Positioning, Navigation, and Timing) for providing navigation integrity to GNSS (Global Navigation Satellite System) constellations. LEO mega-constellations, which are positioned between GNSSs and users, offer closer-to-the user geometry, improving performance, reducing the time to alarm (TTA) and enabling integrity monitoring without complex ground segments of any sort. The aim is to use future LEO mega-constellations as integrity monitors for a forthcoming European Global Navigation Satellite System (EGNSS) specifically focused on automotive users, which has minimal onboard satellite capabilities and no ground involvement. This plan builds on earlier studies, anticipating the performance of the upcoming LEO-PNT In-Orbit Demonstration.

1. Introduction

The current navigation systems providing integrity services to GNSS users rely on ground infrastructure to elaborate the integrity information that is broadcasted to the user. LEO (Low-Earth-Orbit) mega-constellations provide a unique infrastructure that could be leveraged to provide alternative navigation systems, such as the LEO-PNT initiative by the ESA. In this paper, we explore options for exploiting the LEO-PNT to deliver new high-integrity navigation systems with no infrastructure on ground, providing time to alarms (TTAs) shorter than 6 s. The LEO-PNT satellites (here called LEOs for short) are used as integrity monitors of the GNSS satellites flying above the GNSS users and transmit integrity information directly to them, thus significantly improving their time to alarm performance.

The bare minimum integrity required is that the LEOs provide information to GNSS users in such a way that they can determine their PVT solution with a bounded error that is not exceeded with a given probability.

2. Exploring the Options

Different integrity concepts can be envisaged depending on the LEO constellation’s capabilities. We explore different system configurations that lead to different LEO constellations capabilities, which are laid out here.

2.1. Option 1: LEO-PNT Supports ARAIM

This is the basic option, in which the LEO-PNT constellation provides additional dual-frequency L-Band ranging measurements with a committed minimum performance and without a bespoke integrity payload. This is of interest for ARAIM users [1], who benefit greatly from the additional geometrical redundancy provided by LEO satellites.

2.2. Option 2: User-Based Integrity with LEO-MEO Observables

This option is based on monitoring the MEO satellites at user level using LEO-MEO L-Band observables. Each LEO-PNT satellite collects LEO-MEO observables and sends these observables or a suitable by-product to the user. Then, the user individually checks each MEO against a particular hypothesis, e.g., against a given threshold, and decides whether to use that MEO satellite for generating the navigation solution.

The user monitors each MEO satellite by using the LEO satellites that are transmitting their products to the user as reference stations. This approach distributes the monitoring functionality between the LEO-PNT constellation and the user. The constellation performs MEO data collection and dissemination, while the user performs integrity processing.

2.3. Option 3: LEO Satellite-Based Integrity

As with the previous option, the LEO satellite collects MEO observables; however, with this option, an integrity monitoring algorithm is run on board the LEO satellite, sending integrity indicators, possibly per MEO, to the user. A voting algorithm would need to be used to modulate false alarms and missed detection probabilities.

2.4. Option 3: LEO Plane-Based Integrity

This option assumes that the LEO constellation is equipped with inter-plane intersatellite links. The LEO satellites on each plane share their LEO-MEO observables. Within each plane there is a selected LEO satellite for each MEO that acts as an MEO monitor. The selected monitor collects all the observables for the MEO, runs the monitoring algorithm, and returns the flag to the rest of the LEO satellites in the plane as their downlink to the user.

2.5. Selection of the Correct Integrity Approach

Table 1. Summary of evaluation following the selection criteria.

	Performance	TTA	Resource (Processing/BW/ISL)
Option 1: ARAIM	In the range of the ARAIM algorithm.	Does not improve TTA, only improves ARAIM performance.	On-board processing: medium. Low Leo-to-user bandwidth: [one ISM per LEO] ISL: N/A
Option 2: User-based integrity	The performance limit is the number of LEOs visible.	The barrier is run by the user with the LEO data that can be provided in real time by the LEO satellite.	On board processing: low. High Leo-to-User bandwidth: [#MEO in LEO-View × #obs per LEO.] ISL: N/A
Option 3: LEO satellite-based	The number of LEOs visible to one MEO is very limited.	Processing on board will use the TTA budget.	On-board processing: high. Medium Leo-to-user bandwidth: [#MEO in LEO-View × 1 flag per LEO.] ISL: N/A
Option 4: LEO plane-based	LEO visibility in each plane is limited to two or three MEOs per LEO.	ISL distribution will take the TTA budget away. Processing on board will use the TTA budget.	On-board processing: high. Medium Leo-to-user bandwidth: [#MEO in LEO-View × 1 flag per LEO.] ISL: Yes

below provides the justification for the proposed selection of option 2, user-based integrity, which has been chosen for further examination in this study and for upcoming projects within orbit demonstrators as it provides the best accuracy with the lowest TTA, very low on-board processing, and without the need for ISL. The downside is that it is highly demanding in the LEO-to-User bandwidth.

Three selection criteria were considered: performance, TTA, and number of on-board resources.

3. User-Based Integrity with LEO-PNT Formulation (Option 2)

3.1. Integrity Concept

In this section, the integrity monitor is discussed in the context of a broader integrity concept. We use Ithaca [2] as a convenient source of a reference for the “Integrity Concept for EGNSS high accuracy”, which explores different users’ requirements and system configurations. We select the road use case presented in

Table 2. Target Integrity Risk (TIR) for road users.

Alert Limit (AL)	Target Integrity Risk (TIR)	Continuity Risk
3 m	1 × 10−5 per hour	1 × 10−5 per hour

.

3.2. LEO-PNT as a Barrier

The LEO-PNT barrier is located within the integrity GNSS FTA of the integrity concept. Ithaca also provides this tree at a convenient level of decomposition. The GNSS top event (loss of integrity) is broken down into two main branches: a Fault-Free Branch that includes the events that may lead to a loss of integrity under fault-free conditions; a Faulty Branch that further decomposes the events that may lead to a loss of integrity under failure conditions.

The integrity monitor will act as a barrier against the failure mode “Undetected (MEO) Satellite Feared Event”, which is located in the faulty branch. Underneath this failure mode node in the tree, we find events such as satellite clock jumps, pseudorange errors, etc. We can assume that between 10 and 20 events like these can be identified, leading to a split of the 1.5 × 10⁻⁶ per hour budget amongst 20 events (in the worst case scenario, assuming the probability is equal for every event), e.g., 7.5 × 10⁻⁸ per hour. This is usually split into the probability of the occurrence (per h) of the feared event and the probability of its missed detection, Pmd. We will assume that the MEO constellation has a probability of occurrence (per h) of 1 × 10⁻⁴ (per h) for each of these events, leading to a probability of missed detection, Pmd, of 7.5 × 10⁻⁴. A conservative value of 1 × 10⁻⁵ for the Pmd is selected to account for other allocations such those related to feared events occurring in the LEO-PNT satellite itself.

The FTA for continuity is not addressed in the Ithaca report, but a budget is required to stablish the false alarm probability of the integrity monitor, the Pfa. We adopt a Pfa of 1 × 10⁻⁵ for this analysis, with the justification that this is of the same magnitude as the Pmd and the Gaussian assumptions can still be checked with these values.

Finally, the magnitude of the feared event that is to be monitored is taken to be 2 m. The justification for this is made using the example of a satellite clock jump: this event is projected to the user in the same manner as it is to the LEO and it exists in the range domain; thus, when the resulting error is below 2 m in magnitude, it is expected to be covered by an AL of 3 m.

With these three values allocated, the LEO-PNT monitor will need to provide the following performances, expressed in terms of ${\mathit{T}}_{\mathit{m}\mathit{o}\mathit{n}}$ and ${\mathit{\sigma }}_{\mathit{m}\mathit{o}\mathit{n},\mathit{i}}$ (see

Table 3. Performance indicators for LEO-PNT integrity monitor.

Inputs for Barrier Design
MDB	Minimum Detectable Bias to be detected with the probability of missed detection	2 m
Pmd	Probability of missed detection	1 × 10−5
Pfa	Probability of false alarm	1 × 10−5
Output Barrier Performance Indicators
${\mathit{T}}_{\mathit{m}\mathit{o}\mathit{n}}$	Monitoring Threshold: the threshold at which the barrier is triggered	1.13 m
${\mathit{\sigma }}_{\mathit{m}\mathit{o}\mathit{n},\mathit{i}}$	Monitoring Accuracy or sigma monitor, derived from MDB, Pfa, and Pmd	0.19 m

).

3.3. LEO-PNT Error Budget

The LEO-PNT’s barrier performance relies on the quality of the MEO observables collected by the LEO satellites and the geometry that the LEO constellation provides to the user.

Table 4. Error budget.

	Concept	Budget (1 Sigma, m)	Justification
A	Accuracy of real-time LEO position solution	0.1	This is considered feasible using the HAS service [3]
B	Accuracy of real-time LEO synchronization solution	0.15
C	Phase noise	0.005	This value is typical for on-board receivers such as PODRIX in the iono-free combination [4]
	Derived LERE Budget (From A, B, C, and D)
E	Phase LERE	0.18 (0.23)	$\mathrm{LERE} \mathrm{for} \mathrm{phase} \mathrm{users} (\sqrt{A^2+B^2+C^2}$)

presents the LEO Equivalent Ranging Error (LERE) budget. The first two terms (A and B) are the LEO satellite’s position and synchronization. The next two terms (C and D) are the phase and code noise for the iono-free combination. Finally, these terms are added quadratically to derive the phase and code LERE in rows E and F, respectively. The more conservative values in brackets are used in the simulations to account for some uncertainties not considered in this simple budget, such as multipath errors.

3.4. User Equations

3.4.1. Basic LEO Barrier Formulation

MEO to LEO Observations

The observation residual at a given epoch for MEO i–LEO l is expressed as follows:

$$y_{i,l}={\mathit{v}}_{i,l}^T·{\mathit{x}}_i+{ϵ}_{i,l}$$

(1)

where

${\mathit{v}}_{i,l}^T$ is the unit vector from the LEO satellite $l$ to the MEO satellite i.

${\mathit{x}}_i$ is the error in the MEO’s position and clock according to the SiS.

${ϵ}_{i,l}$ is the LEO to MEO observation noise considering the LEO PNT’s Rx and environment, e.g., LERE. It is modelled as a normal distribution ${ϵ}_{i,l}~N\left(0,w_{i,l}^{-1}\right)$, with $w_{i,l}^{-1}$ being the covariance of the MEO i–LEO l observation noise. This situation is depicted in Figure 1.

Basic LEO Barrier

A user will collect from the LEO satellites all the MEO-LEO residuals and run one barrier per MEO satellite. Stacking up the equations for each MEO-LEO observation yields

$$\begin{gathered} {\mathit{y}}_{\mathit{i}}=\left[\begin{array}{c}{y}_{i,1}\\ \dots \\ y_{i,L}\end{array}\right]=\left[\begin{array}{c}{\mathit{v}}_{i,1}^T\\ \dots \\ {\mathit{v}}_{i,L}^T\end{array}\right]{\mathit{x}}_i+\left[\begin{array}{c}{ϵ}_{i,1}\\ \dots \\ {ϵ}_{i,L}\end{array}\right]={\mathit{C}}_{\mathit{i}}·{\mathit{x}}_i+{\mathit{ϵ}}_{\mathit{i}} \\ l=\left\{1,L\right\} LEOs in view of the User and of MEO i \end{gathered}$$

(2)

Now this user will run a barrier for the MEO satellite i. Here, a weighted LSQ barrier is taken as a reference:

$${\widehat{\mathit{x}}}_i={\left({\mathit{C}}_{\mathit{i}}^T{\mathit{W}}_{{\mathit{L}}_i} {\mathit{C}}_i\right)}^{-1}{\mathit{C}}^T{\mathit{W}}_{{\mathit{L}}_i}{\mathit{y}}_{\mathit{l}}$$

(3)

with $\mathbf{E}\left[{\mathit{ϵ}}_i{\mathit{ϵ}}_i^T\right]={\mathit{W}}_{{\mathit{L}}_i}$.

The user will perform a check on ${\widehat{\mathit{x}}}_i$ (e.g., $\left|{{\mathit{u}}_i^T\widehat{\mathit{x}}}_i\right|<T_{mon}$) and decide whether to include or exclude the satellite. The objective of the barrier is to evaluate the covariance involved in the MEO position error estimation process, and the performance of the LEO barrier is measured with the sigma monitor ${\sigma }_{mon,i}$, which is the projection of the ${\widehat{\mathit{x}}}_i-{\mathit{x}}_i$ covariance on the user in direction ${\mathit{u}}_{\mathit{i}}$:

$${\sigma }_{mon,i}^2={\mathit{u}}_{\mathit{i}}^{\mathit{T}}\mathbf{E}\left[\left({\widehat{\mathit{x}}}_i-{\mathit{x}}_i\right){\left({\widehat{\mathit{x}}}_i-{\mathit{x}}_i\right)}^T\right]{\mathit{u}}_{\mathit{i}}={\mathit{u}}_{\mathit{i}}^{\mathit{T}}{\left({\mathit{C}}_{\mathit{i}}^T{\mathit{W}}_{{\mathit{L}}_i}{\mathit{C}}_i\right)}^{-1}{\mathit{u}}_{\mathit{i}}$$

(4)

3.4.2. A Priori LEO Barrier Formulation

A Priori LEO Barrier

The Basic LEO Barrier in Equation (4) requires a large amount of LoS to provide a low-covariance matrix and an accurate estimation of ${\widehat{\mathit{x}}}_i-{\mathit{x}}_i$. Usually, this is overcome by using time filtering, and the most popular options are WLSQ with a priori information and the Kalman filter. Since we are aiming for a low TTA, we opt for the WLSQ with a priori information, where the a priori covariance matrix remains constant over time and allows us to better ensure a detectability time.

The state vector ${\mathit{x}}_i$ from epoch t is here renamed as $\mathbf{\Delta }{\mathit{X}}_{\mathit{t}}$. At epoch t, we start with the state vector from the previous epoch t − 1, $\mathbf{\Delta }{\mathit{X}}_{\mathit{t}-\mathbf{1}}$. The a priori covariance matrix of $\mathbf{\Delta }{\mathit{X}}_{\mathit{t}-\mathbf{1}}$ is ${\mathit{P}}_{\mathbf{0}}^{-\mathbf{1}}$. In this case, it can be demonstrated that

$$\begin{gathered} {\widehat{\mathit{x}}}_{\mathit{i}}=\mathbf{\Delta }{\mathit{X}}_{\mathit{t}}={\left({\mathit{C}}_{\mathit{i}}^{\mathit{T}}{\mathit{W}}_{{\mathit{L}}_i}{\mathit{C}}_{\mathit{i}}+{\mathit{P}}_{\mathbf{0}}\right)}^{-\mathbf{1}}\left({\mathit{C}}^{\mathit{T}}{\mathit{W}}_{{\mathit{L}}_i}{\mathit{y}}_{\mathit{l}}+{\mathit{P}}_{\mathbf{0}}\mathbf{\Delta }{\mathit{X}}_{\mathit{t}-\mathbf{1}}\right) \\ {\mathit{\sigma }}_{\mathit{m}\mathit{o}\mathit{n},\mathit{i}}^{\mathbf{2}}={\mathit{u}}_{\mathit{i}}^{\mathit{T}}\mathbf{E}\left[\left({\widehat{\mathit{x}}}_{\mathit{i}}-{\mathit{x}}_{\mathit{i}}\right){\left({\widehat{\mathit{x}}}_{\mathit{i}}-{\mathit{x}}_{\mathit{i}}\right)}^{\mathit{T}}\right]{\mathit{u}}_{\mathit{i}}={\mathit{u}}_{\mathit{i}}^{\mathit{T}}{\left({\mathit{C}}_{\mathit{i}}^{\mathit{T}}{\mathit{W}}_{{\mathit{L}}_i}{\mathit{C}}_{\mathit{i}}+{\mathit{P}}_{\mathbf{0}}\right)}^{-\mathbf{1}}{\mathit{u}}_{\mathit{i}} \end{gathered}$$

(5)

The detectability of the barrier is not compromised significantly as long as the following are true:

• ${\mathit{P}}_{\mathbf{0}}$ is “smaller” than ${\mathit{W}}_{{\mathit{L}}_i}$ in terms of their diagonal elements;
• The LEO constellation’s altitude is low enough that the user–MEO geometry is like the LEO-MEO geometry.

3.5. Performance Assessment

3.5.1. Methodology

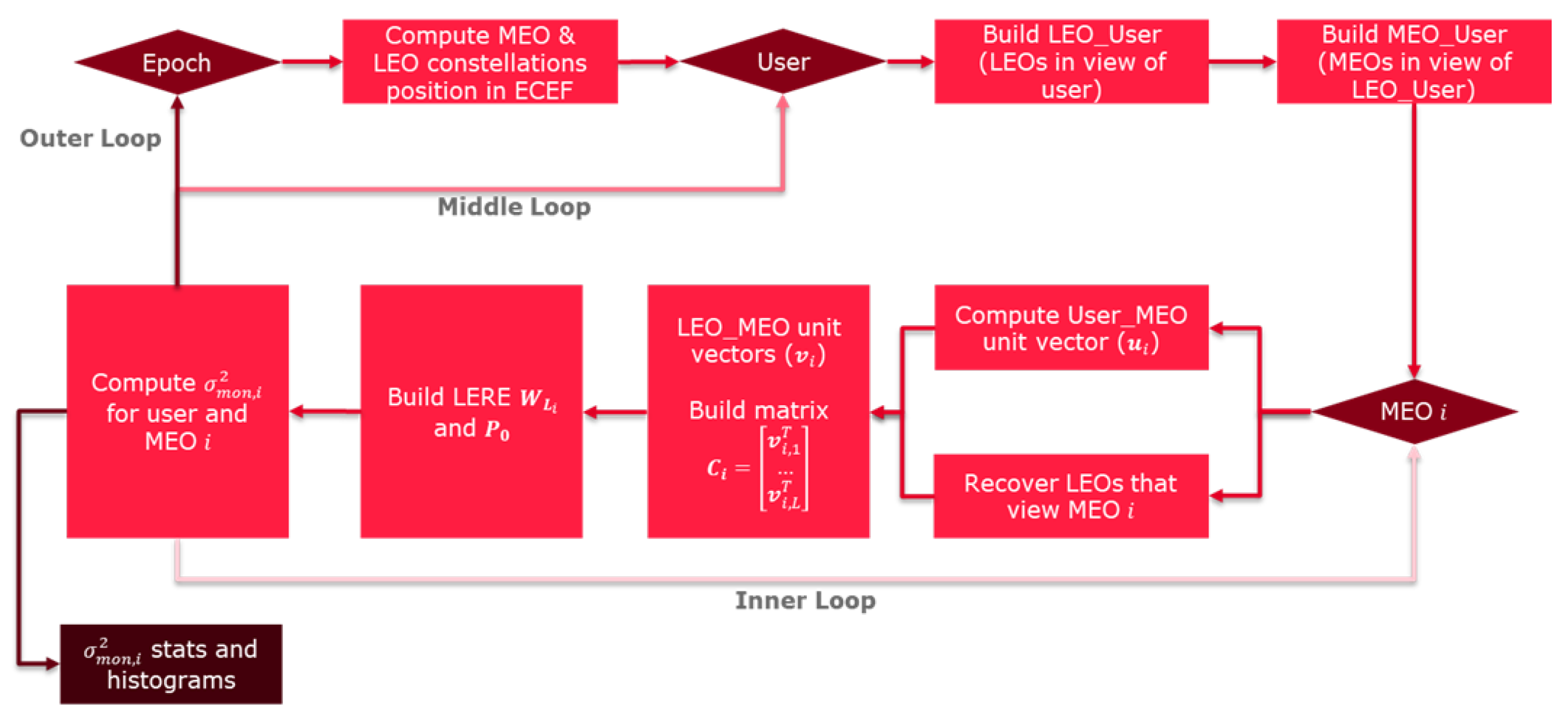
A Service Volume Simulator, SVS, has been developed in Python 3.11.6 to analyze the performance of the integrity monitor.

The SVS’s process is shown in Figure 2.

3.5.2. LEO Constellations

In earlier studies, these strategies were analyzed over full LEO constellations containing 200–400 satellites, such as the HIGH_LEO constellation (

Table 5. Constellation definition.

Constellation ID	Number of Satellites	Number of Planes	Altitude [km]	Inclination [deg]
HIGH_LEO (220 satellites)	42	6	1200	80
	81	9	1200	65
	49	7	1200	50
	48	8	1200	10
IoD (4 satellites)	4	2	561	97.6354

). It would be interesting to evaluate the different algorithms in a less standard constellation, one that can be tested in orbit without spending millions of dollars. For that, the “IoD constellation” has been defined, as shown in Table 5.

3.5.3. Simulation Results

The following results are from the 1-day SVS simulation run for a 20 × 20 user grid with a time step of 1 h.

Basic LEO Barrier Results

Table 6. Basic barrier results comparison for full constellation (left) and IoD constellation (right).

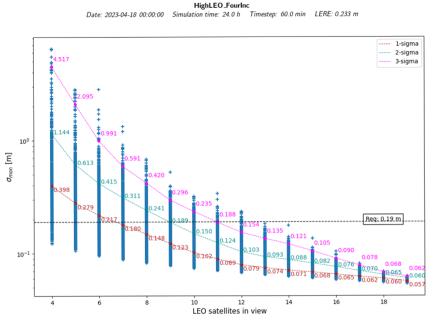
Full Constellation Performance	IOD Constellation Performance

shows the comparison of the basic sigma monitor, as a function of the LEOs in view, and the phase LERE budget for both the full constellation and the IoD constellation. The 19 cm target of the sigma monitor is achieved 95% of the time (2-sigma) when there are 9 LEOs or more in view. This geometry distribution depends only on the constellation’s configuration and the analyzed epoch. For a constellation with only four satellites, this approach does not return relevant results, since there are not enough satellites visible to the user to make the barrier work.

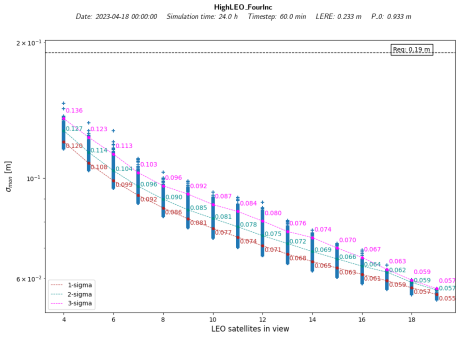
A Priori Results

The a priori sigma monitor is simulated here with a diagonal matrix that is 16 times the noise value. The distribution of the sigma monitor across the full constellation in

Table 7. A priori results comparison for full constellation (left) and IoD constellation (right).

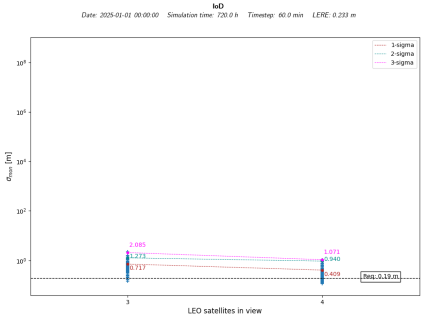
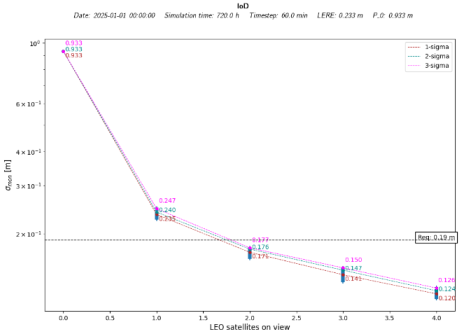
Full Constellation Performance	IOD Constellation Performance

shows that the required sigma monitor is always achieved. This is not the case for the IoD constellation; however, the required sigma monitor is achieved with only two satellites in view, so not as many lines of sight are required.

IoD Global Results

In

Table 8. Summary of results from a priori strategy for IoD simulations.

LEO Barrier	LERE Value [cm]	$\mathit{w}/\mathit{p}$ Ratio	Number of Satellites Used to Meet Requirements (0.19 m) at 67/95/99.7 Percentile		Sigma Monitor Values [m] Achieved at 67/95/99.7 Percentile		Time % with Less Satellites Than Required
A priori	23 cm	4	67.0%	2	67.0%	0.21	38.264
			95.0%	2	95.0%	0.47	38.264
			99.7%	2	99.7%	-	38.264
		16	67.0%	2	67.0%	0.23	38.264
			95.0%	2	95.0%	0.93	38.264
			99.7%	2	99.7%	-	38.264
		100	67.0%	3	67.0%	0.25	48.553
			95.0%	4	95.0%	2.33	75.563
			99.7%	4	99.7%	-	75.563
	50 cm	4	67.0%	-	67.0%	0.46	-
			95.0%	-	95.0%	1.03	-
			99.7%	-	99.7%	-	-
		16	67.0%	-	67.0%	0.5	-
			95.0%	-	95.0%	2.06	-
			99.7%	-	99.7%	-	-
		100	67.0%	-	67.0%	0.55	-
			95.0%	-	95.0%	5.14	-
			99.7%	-	99.7%	-	-

, the results obtained from this set of simulations are presented. These simulations last 1 day, with a timestep of 1 h over one relevant user location in the ESTEC (ESA), and use the a priori approach with different noise configurations. The a priori matrix’s diagonal elements vary from 2 to 10 times the noise value. As this case is quite extreme, restrictive conditions must be applied to make the barrier work, but this is possible and allows us to test our strategies using low-budget demonstrators. Note that bold is used to highlight the best case scenario.

4. Conclusions

This paper explores the different options for providing GNSS integrity services when using only an LEO mega-constellation as infrastructure. This study has focused on an automotive user whose integrity FTA has been reused from the Ithaca project. The integrity monitor has been contextualized in this FTA and dimensioned in terms of MDB, Pmd, and Pfa.

The barrier required for the integrity monitor has been identified and formulated in three different manners, considering a basic WLSQ approach with a priori information. The impact of the a priori formulation on the responsiveness of the barrier (and therefore the TTA) has been initially addressed using a simple example. The error budget for the GNSS on board the LEO mega-constellation has also been analyzed.

Based on the results obtained with the simulations run by the SVS, it can be concluded that the targeted sigma monitor of 19 cm, resulting from the MDB, Pfa, and Pmd analyses, is achievable, especially when considering the mega-constellations that are projected, which encourages us to continue improving the concept of integrity by utilizing LEO satellites.