Geometric Analysis of LEO-Based Monitoring of GNSS Constellations †
Abstract
1. Introduction
2. Methodology
2.1. Geometrical Analysis
2.1.1. Availability
2.1.2. Dilution of Precision (DOP)
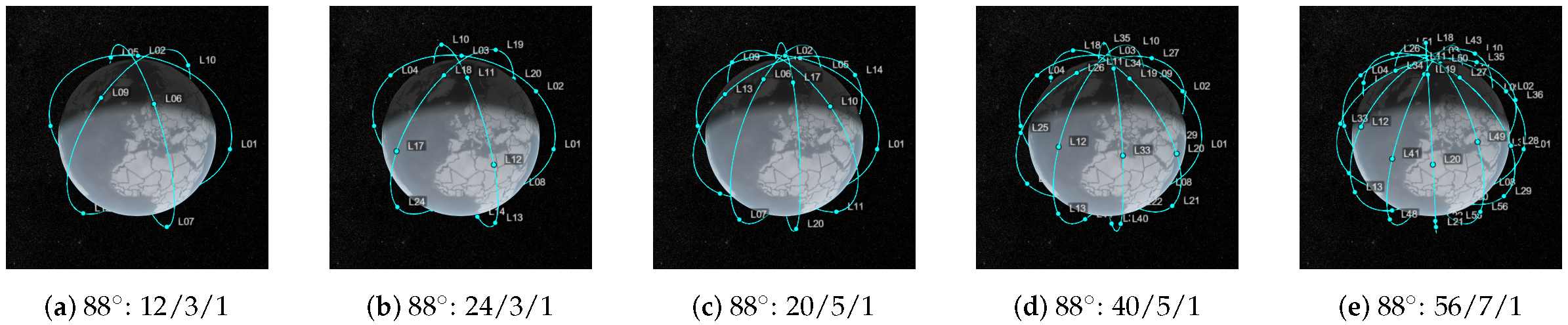
2.2. Simulation Environment
3. Results
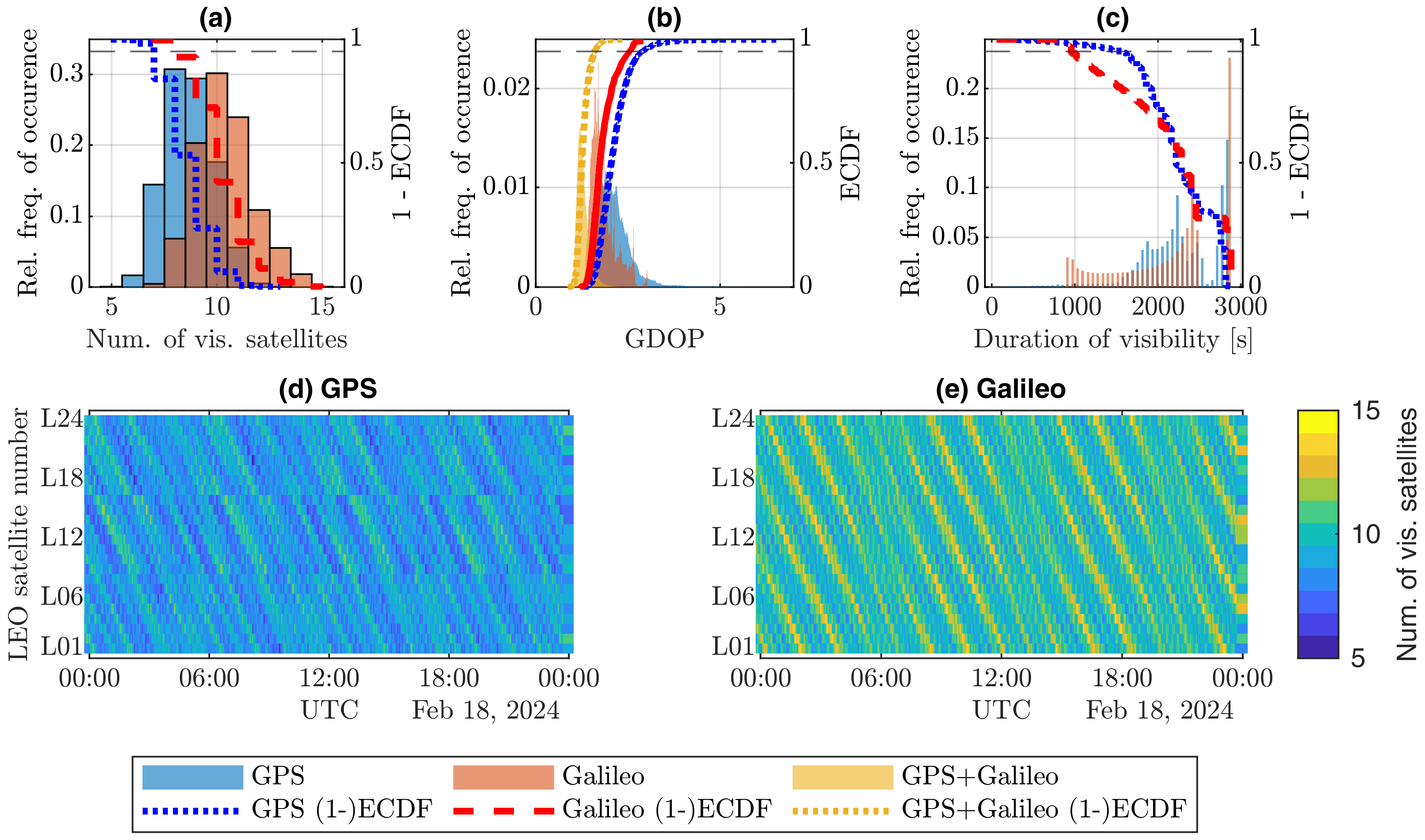
3.1. Visibility
3.2. Observability
3.3. Overview
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reid, T.G.; Chan, B.; Goel, A.; Gunning, K.; Manning, B.; Martin, J.; Neish, A.; Perkins, A.; Tarantino, P. Satellite Navigation for the Age of Autonomy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 342–352. [Google Scholar] [CrossRef]
- González, A.; Tobías; Rodriguez, I.; Navarro, P.; Sobrero, F.; Carbonell, E.; Calle, D.; Fernández, J. LEO Satellites for PNT, the Next Step for Precise Positioning Applications. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 2573–2581. [Google Scholar] [CrossRef]
- Ries, L.; Limon, M.C.; Grec, F.C.; Anghileri, M.; Prieto-Cerdeira, R.; Abel, F.; Miguez, J.; Perello-Gisbert, J.V.; D’addio, S.; Ioannidis, R.; et al. LEO-PNT for Augmenting Europe’s Space-based PNT Capabilities. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023. [Google Scholar]
- Catalán, C.C.; Iglesias, L.G.; Muñoz, A.J.; Matamala, E.F.; Berges, C.P.; Moreno, A.M.; Gassió, M.P.; Fort, E.A.; Samper, M.D.L.; Álvarez, J.B.; et al. Integrity Monitoring of GNSS with LEO Satellites to Reduce the Time to Alarm. In Proceedings of the 36th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 2282–2309. [Google Scholar]
- Morales-Ferre, R.; Lohan, E.S.; Falco, G.; Falletti, E. GDOP-based Analysis of Suitability of LEO Constellations for Future Satellite-Based Positioning. In Proceedings of the 2020 Annual IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Vicenza, Italy, 12–14 October 2020; pp. 147–152. [Google Scholar]
- Ge, H.; Li, B.; Jia, S.; Nie, L.; Wu, T.; Yang, Z.; Shang, J.; Zheng, Y.; Ge, M. LEO Enhanced Global Navigation Satellite System (LeGNSS): Progress, Opportunities, and Challenges. Geo-Spat. Inf. Sci. 2022, 25, 1–13. [Google Scholar] [CrossRef]
- Ferre, R.M.; Lohan, E.S. Comparison of MEO, LEO, and Terrestrial IoT Configurations in Terms of GDOP and Achievable Positioning Accuracies. IEEE J. Radio Freq. Identif. 2021, 5, 287–299. [Google Scholar] [CrossRef]
- Dufour, F.; Bertrand, R.; Sarda, J.; Lasserre, E.; Bernussou, J. Constellation Design Optimization with a DOP Based Criterion. In Proceedings of the 14th International Symposium on Space Flight Dynamics, Foz do Iguaçu, Brazil, 8–12 February 1999. [Google Scholar]
- Casanova, D.; Avendaño, M.; Mortari, D. Seeking GDOP-optimal Flower Constellations for Global Coverage Problems through Evolutionary Algorithms. Aerosp. Sci. Technol. 2014, 39, 331–337. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Nie, L.; Ge, M.; Schuh, H. LEO Constellation Optimization for LEO Enhanced Global Navigation Satellite System (LeGNSS). Adv. Space Res. 2020, 66, 520–532. [Google Scholar] [CrossRef]
- Marchionne, L.; Gessato, L.M.; Toni, F.; Barbera, S.L. Striking a Balance: Performance and Cost Optimization of LEO-PNT Constellation for Hybrid Users Using a Meta-Heuristic Approach. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace, MetroAeroSpace 2023—Proceedings, Milan, Italy, 19–21 June 2023; pp. 609–614. [Google Scholar] [CrossRef]
- Jan, S.S.; Chan, W.; Walter, T. MATLAB Algorithm Availability Simulation Tool. GPS Solut. 2009, 13, 327–332. [Google Scholar] [CrossRef]
- González, Á. Measurement of Areas on a Sphere Using Fibonacci and Latitude–Longitude Lattices. Math. Geosci. 2010, 42, 49–64. [Google Scholar] [CrossRef]





| Parameter | Used Value |
|---|---|
| Initial time | 2024-02-18 00:00 UTC |
| End time | 2024-03-19 00:00 UTC |
| Simulation rate | 60 |
| Orbit propagator | Two-body Keplerian |
| Satellite Constellations | GPS, Galileo, and LEO |
| GPS Almanac File | MAAST almgps24+3.txt |
| Galileo Almanac File | MAAST almgalileo.txt |
| 36/3/1 | 35/5/1 | 35/7/1 | ||||
|---|---|---|---|---|---|---|
| Num. vis. GPS | 7 | (5, 9, 13) | 7 | (4, 9, 13) | 7 | (4, 9, 13) |
| Num. vis. GAL | 8 | (7, 10, 15) | 7 | (6, 10, 15) | 7 | (6, 10, 15) |
| Vis. dur. GPS [min] | 26 | (1, 37, 48) | 22 | (1, 37, 49) | 22 | (1, 37, 48) |
| Vis. dur. GAL [min] | 16 | (1, 39, 48) | 22 | (1, 35, 48) | 24 | (1, 39, 48) |
| GDOP GPS | 2.9 | (1.3, 2.0, 6.6) | 2.9 | (1.2, 2.0, 47) | 2.9 | (1.2, 2.0, 51) |
| GDOP GAL | 2.5 | (1.2, 1.7, 3.0) | 2.6 | (1.2, 1.8, 3.3) | 2.6 | (1.2, 1.8, 3.3) |
| GDOP GPS+GAL | 1.6 | (0.9, 1.3, 2.4) | 1.6 | (0.9, 1.3, 2.7) | 1.6 | (0.9, 1.3, 2.6) |
| Num. LEO obs. GPS | 8 | (7, 12, 15) | 8 | (6, 12, 15) | 8 | (5, 12, 15) |
| Num. LEO obs. GAL | 9 | (8, 12, 15) | 8 | (6, 11, 15) | 8 | (5, 11, 14) |
| Obs. PDOP GPS | 3.2 | (2.1, 2.7, 3.8) | 3.3 | (2.1, 2.7, 4.1) | 3.2 | (2.2, 2.8, 12) |
| Obs. PDOP GAL | 3.6 | (2.6, 3.2, 3.9) | 3.8 | (2.6, 3.2, 4.7) | 3.7 | (2.6, 3.3, 14) |
| 12/3/1 | 24/3/1 | 20/5/1 | 40/5/1 | 28/7/1 | 56/7/1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Num. vis. GPS | 7 | (5, 9, 13) | 7 | (5, 9, 13) | 7 | (5, 9, 13) | 7 | (4, 9, 13) | 7 | (5, 9, 13) | 7 | (5, 9, 13) |
| Num. vis. GAL | 9 | (7, 11, 15) | 9 | (7, 11, 15) | 8 | (6, 10, 15) | 8 | (6, 10, 15) | 8 | (6, 10, 15) | 8 | (6, 10, 15) |
| Vis. dur. GPS [min] | 24 | (1, 34, 42) | 24 | (1, 34, 42) | 21 | (1, 34, 42) | 21 | (1, 34, 43) | 21 | (1, 34, 43) | 21 | (1, 34, 43) |
| Vis. dur. GAL [min] | 17 | (1, 35, 43) | 17 | (1, 35, 43) | 21 | (1, 35, 43) | 21 | (1, 36, 43) | 22 | (1, 36, 43) | 22 | (1, 36, 43) |
| GDOP GPS | 2.8 | (1.2, 2.0, 6.0) | 2.8 | (1.2, 2.0, 6.2) | 2.8 | (1.2, 2.0, 8.5) | 2.8 | (1.2, 2.0, 18) | 2.8 | (1.2, 2.0, 14) | 2.8 | (1.2, 2.0, 14) |
| GDOP GAL | 2.5 | (1.2, 1.7, 3.1) | 2.5 | (1.2, 1.7, 3.1) | 2.6 | (1.2, 1.8, 3.4) | 2.6 | (1.2, 1.8, 3.4) | 2.6 | (1.2, 1.8, 3.4) | 2.6 | (1.2, 1.8, 3.4) |
| GDOP GPS+GAL | 1.5 | (0.9, 1.2, 2.3) | 1.5 | (0.9, 1.2, 2.4) | 1.6 | (0.9, 1.3, 2.6) | 1.6 | (0.9, 1.3, 2.5) | 1.6 | (0.9, 1.2, 2.5) | 1.6 | (0.9, 1.2, 2.6) |
| Num. LEO obs. GPS | 2 | (2, 4, 6) | 6 | (4, 8, 12) | 4 | (3, 7, 10) | 10 | (8, 14, 20) | 6 | (4, 10, 14) | 14 | (10, 19, 25) |
| Num. LEO obs. GAL | 3 | (2, 4, 6) | 6 | (5, 8, 10) | 4 | (3, 6, 10) | 9 | (8, 13, 16) | 6 | (5, 9, 13) | 13 | (11, 19, 23) |
| Obs. PDOP GPS | 9.8 | (3.6, 5.9, ∞) | 1.3 | (0.9, 1.1, 1.7) | 2.3 | (1.0, 1.3, ∞) | 1.0 | (0.7, 0.9, 1.2) | 1.8 | (0.9, 1.1, 4.6) | 0.8 | (0.6, 0.7, 1.1) |
| Obs. PDOP GAL | 11 | (4.3, 7.3, ∞) | 1.3 | (1.0, 1.2, 1.5) | 2.6 | (1.0, 1.4, ∞) | 1.0 | (0.8, 0.9, 1.1) | 2.0 | (0.9, 1.1, 4.0) | 0.8 | (0.7, 0.7, 0.9) |
| 12/3/1 | 24/3/1 | 20/5/1 | 40/5/1 | 28/7/1 | 56/7/1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Num. vis. GPS | 7 | (4, 9, 13) | 7 | (5, 9, 13) | 7 | (4, 9, 13) | 7 | (4, 9, 13) | 7 | (4, 9, 13) | 7 | (4, 9, 13) |
| Num. vis. GAL | 8 | (7, 10, 15) | 8 | (7, 10, 15) | 7 | (6, 10, 15) | 7 | (6, 10, 15) | 7 | (6, 10, 15) | 7 | (6, 10, 15) |
| Vis. dur. GPS [min] | 26 | (1, 37, 48) | 26 | (1, 37, 48) | 22 | (1, 37, 49) | 22 | (1, 37, 49) | 23 | (1, 37, 48) | 22 | (1, 37, 48) |
| Vis. dur. GAL [min] | 16 | (1, 39, 48) | 16 | (1, 39, 48) | 22 | (1, 39, 48) | 22 | (1, 39, 48) | 24 | (1, 39, 48) | 24 | (1, 39, 48) |
| GDOP GPS | 2.7 | (1.2, 2.0, 5.9) | 2.8 | (1.2, 2.0, 6.2) | 2.8 | (1.2, 2.0, 8.5) | 2.8 | (1.2, 2.0, 17) | 2.8 | (1.2, 2.0, 14) | 2.8 | (1.2, 2.0, 14) |
| GDOP GAL | 2.7 | (1.2, 1.7, 3.1) | 2.5 | (1.2, 1.7, 3.1) | 2.6 | (1.2, 1.8, 3.3) | 2.6 | (1.2, 1.8, 3.4) | 2.6 | (1.2, 1.8, 3.4) | 2.6 | (1.2, 1.8, 3.4) |
| GDOP GPS+GAL | 1.5 | (0.9, 1.2, 2.3) | 1.5 | (0.9, 1.2, 2.4) | 1.5 | (0.9, 1.3, 2.6) | 1.5 | (0.9, 1.3, 2.5) | 1.6 | (0.9, 1.2, 2.5) | 1.6 | (0.9, 1.2, 2.6) |
| Num. LEO obs. GPS | 2 | (2, 4, 6) | 5 | (4, 8, 12) | 4 | (3, 7, 10) | 9 | (6, 13, 19) | 6 | (4, 9, 14) | 13 | (10, 19, 25) |
| Num. LEO obs. GAL | 2 | (2, 4, 6) | 6 | (4, 8, 9) | 4 | (3, 6, 10) | 9 | (6, 13, 15) | 6 | (4, 9, 13) | 13 | (11, 18, 21) |
| Obs. PDOP GPS | 3.4 | (1.3, 2.6, ∞) | 4.0 | (2.4, 3.3, 5.5) | 2.4 | (1.0, 1.3, ∞) | 1.0 | (0.7, 0.9, 1.3) | 1.9 | (0.9, 1.1, 4.6) | 0.8 | (0.6, 0.7, 1.1) |
| Obs. PDOP GAL | 4.0 | (1.4, 2.5, ∞) | 4.9 | (3.2, 3.9, 6.2) | 2.7 | (1.1, 1.4, ∞) | 1.0 | (0.8, 0.9, 1.3) | 2.1 | (0.9, 1.1, 4.6) | 0.8 | (0.7, 0.7, 1.0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oezmaden, C.; García Crespillo, O.; Niestroj, M.; Brachvogel, M.; Meurer, M. Geometric Analysis of LEO-Based Monitoring of GNSS Constellations. Eng. Proc. 2025, 88, 57. https://doi.org/10.3390/engproc2025088057
Oezmaden C, García Crespillo O, Niestroj M, Brachvogel M, Meurer M. Geometric Analysis of LEO-Based Monitoring of GNSS Constellations. Engineering Proceedings. 2025; 88(1):57. https://doi.org/10.3390/engproc2025088057
Chicago/Turabian StyleOezmaden, Can, Omar García Crespillo, Michael Niestroj, Marius Brachvogel, and Michael Meurer. 2025. "Geometric Analysis of LEO-Based Monitoring of GNSS Constellations" Engineering Proceedings 88, no. 1: 57. https://doi.org/10.3390/engproc2025088057
APA StyleOezmaden, C., García Crespillo, O., Niestroj, M., Brachvogel, M., & Meurer, M. (2025). Geometric Analysis of LEO-Based Monitoring of GNSS Constellations. Engineering Proceedings, 88(1), 57. https://doi.org/10.3390/engproc2025088057






