Abstract
A core problem relating to indoor positioning is a lack of prior knowledge of the environment. To date, most WiFi–RTT research assumes knowledge of the access points in an indoor environment. This paper provides a solution to this problem by using a simultaneous localisation and mapping (SLAM) algorithm, using WiFi–RTT and pedestrian dead reckoning, which uses the inertial sensors in a smartphone. A WiFi–RTT SLAM algorithm has only been researched in one instance at the time of writing; this paper aims to expand the exploration of this problem, particularly in relation to the use of outlier detection and motion models. For the trials, which were 35 steps long, the final mobile device horizontal positioning error was 1.01 m and 1.7 m for the forward and reverse trials, respectively. The results of this paper show that unmapped indoor positioning using WiFi–RTT is feasible for metre-level indoor positioning, given correct access point calibration.
1. Introduction and Background
WiFi is used to carry out mobile indoor positioning, primarily because it has vast infrastructure presence and a typically static access point (AP) location. WiFi fine time measurement (FTM) is a WiFi protocol that enables the time of flight (ToF) of a WiFi signal to be determined. The system that applies this protocol is commonly referred to as WiFi fine time measurement (FTM) and round-trip timing (WiFi–RTT) [1]. This protocol has allowed ToF-based positioning algorithms to be applied to WiFi signals, which is a key step to enabling more accurate and reliable indoor positioning than WiFi received signal strength indicator (RSSI)-based positioning. This technique has the potential to achieve reliable sub-metre accuracy in indoor environments [2]. Non-line-of-sight (NLOS) reception and multipath interference are inevitable in complex indoor environments and degrade WiFi–RTT accuracy. Raja and Groves [3] explored filtering techniques and RSSI-based outlier detection at ION GNSS+ 2023 to mitigate these issues and to demonstrate WiFi–RTT as a reliable positioning solution.
WiFi–RTT-based positioning has been explored by several different authors. Gentner et al. [4] reviewed the distribution of the WiFi–RTT distance estimation errors and developed a Gaussian mixture model. This model was then used in a particle filter. In an experiment involving a person carrying the mobile device that was being tracked, the average positioning error was found to be 0.93 m with a standard deviation of 0.88 m, which is an improvement of 0.45 m compared to the model using a standard Gaussian measurement model, which had a standard deviation of 0.95 m. Guo et al. [5] opted for a different approach that revolved around a hybrid RSSI and RTT model. The paper compared RSSI fingerprinting against a Kalman filter using WiFi–RTT ranging data. The average positioning error of the fingerprinting was 3.41 m with a standard deviation of 1.993 m, whilst the Kalman filter had an error of 2.04 m and a standard deviation of 1.286 m for the same environment. When an RSSI outlier detection method was used, the positioning error of the RTT-based Kalman filter improved to 1.44 m with a standard deviation of 0.819 m. Sun et al. [6] integrated pedestrian dead reckoning (PDR) with WiFi–RTT in an extended Kalman filter. This method achieved an average positioning error of 0.98 m and an average RMSE of 1.1 m. Whilst the performance of the algorithms developed for the discussed papers was promising, all papers assumed that the location of the APs was known. This is a key limitation of indoor positioning as it results in a lengthy data collection phase that can be impractical at scale.
Gentner and Avram [7] developed a WiFi–RTT simultaneous localisation and mapping (SLAM) model. Within WiFi–RTT-based positioning, this is the first paper that does not assume prior knowledge of the environment such as the location of APs or a fingerprint database. This model follows a SLAM approach with a particle filter, and fuses WiFi–RTT ranging measurements with IMU data from the same mobile device; the model simultaneously estimates the AP locations and the position of the mobile device. Gentner and Avram [7] highlight the importance of using a particle filter over a low-complexity extended Kalman filter due to the non-linearity of the measurements. The estimated mobile device position using this method had a root mean square error below 1 m. This demonstrates the feasibility of SLAM when applied to WiFi–RTT and is a strong basis for the research explored in this paper. Gentner and Avram did not explore any outlier detection methods and, more importantly, did not use a pedestrian dead reckoning model for estimating the movement of the pedestrian, instead using a set of fixed markers with a known position in the environment.
This paper aims to provide a WiFi–RTT-based pedestrian navigation solution that makes no assumption of the location of APs by using simultaneous localisation and mapping (SLAM).
The research in this paper explores the accuracy of WiFi–RTT SLAM pedestrian navigation when applied to indoor environments. The algorithm used is FastSLAM [8], which uses a particle filter with sequential importance resampling [9] for obtaining position estimates of the pedestrian holding the moving smartphone and the APs. The algorithm in this paper was augmented with an RSSI-based outlier detection model [3]. The movement of the pedestrian was measured using a pedestrian dead reckoning algorithm. This solely uses the inertial sensors in the smartphone. All methods for orientation and step detection are based on what is provided by the smartphone and Android API [1]. This ensures a more realistic experimental setup. The paper will begin by reviewing the literature published in this research area; then, it will describe the methodology used to demonstrate the accuracy of the algorithm. Finally, the results will be discussed and concluded.
2. Methodology
2.1. FastSLAM
Fast SLAM conceptually follows a similar flow to a particle filter. However, in addition to the particle filter of the mobile device position estimate, each landmark has their own particle filter state with their own position estimate. This means that the estimated position of the landmarks is actually variable and the location estimate is determined as the mobile device moves through the environment. Compared to other SLAM models, FastSLAM is better suited for dealing with different motion and error models that might be non-linear in nature. During the earlier epochs of the SLAM model, the algorithm was more akin to odometry. Due to the uncertainty around the landmark locations, the algorithm relies more heavily on the motion sensors in the earlier epochs of the algorithm. Furthermore, by using particles, the mobile device and landmark states can scale more efficiently whilst dealing with a more complex distribution; this is a general benefit of Monte Carlo-based filters. This means that FastSLAM is well suited for positioning during operation, as the number of particles can be altered to accommodate for computational requirements. Admittedly, this will have an effect on the positioning accuracy.
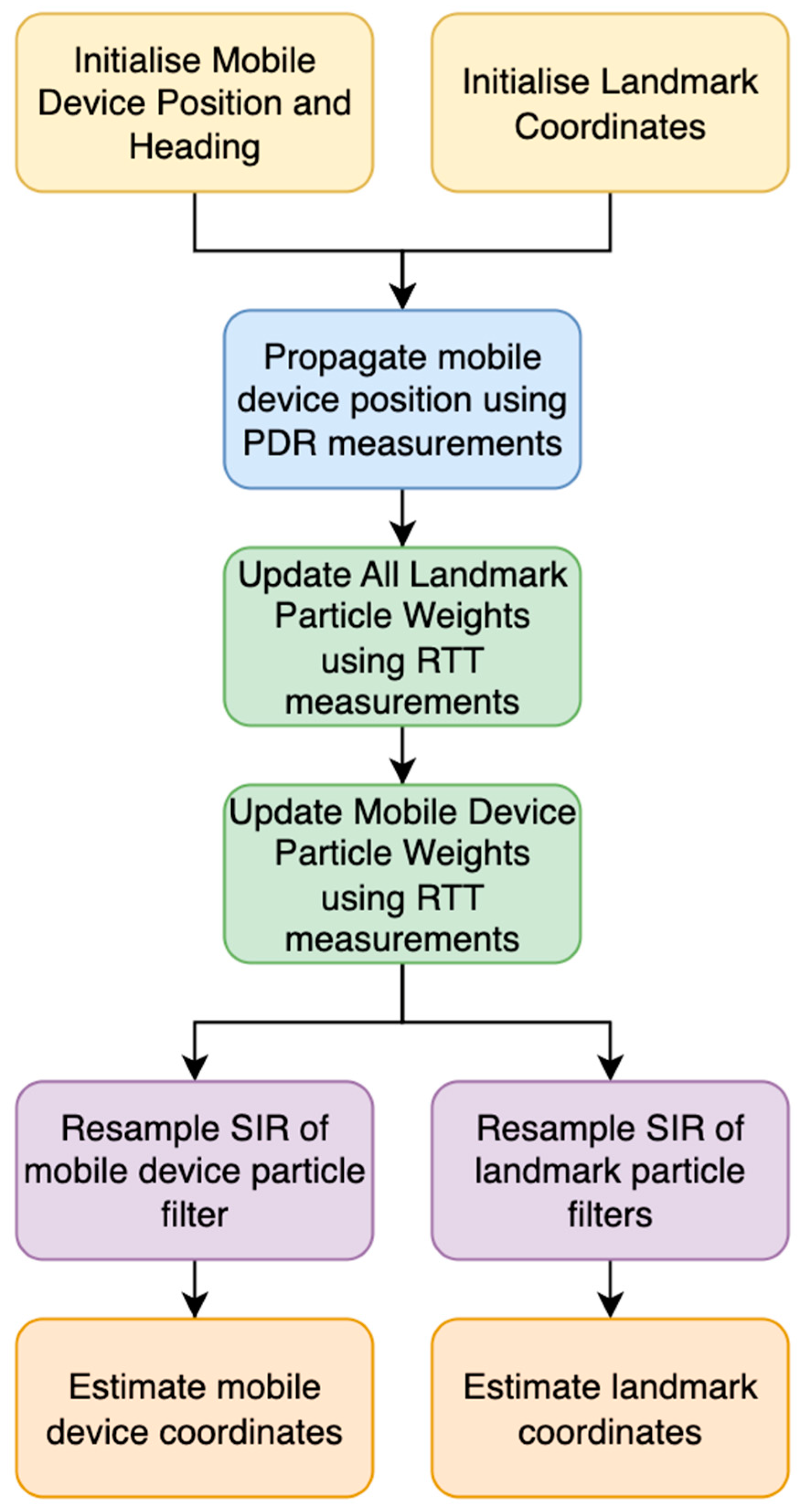
The algorithm follows the process shown in Figure 1.
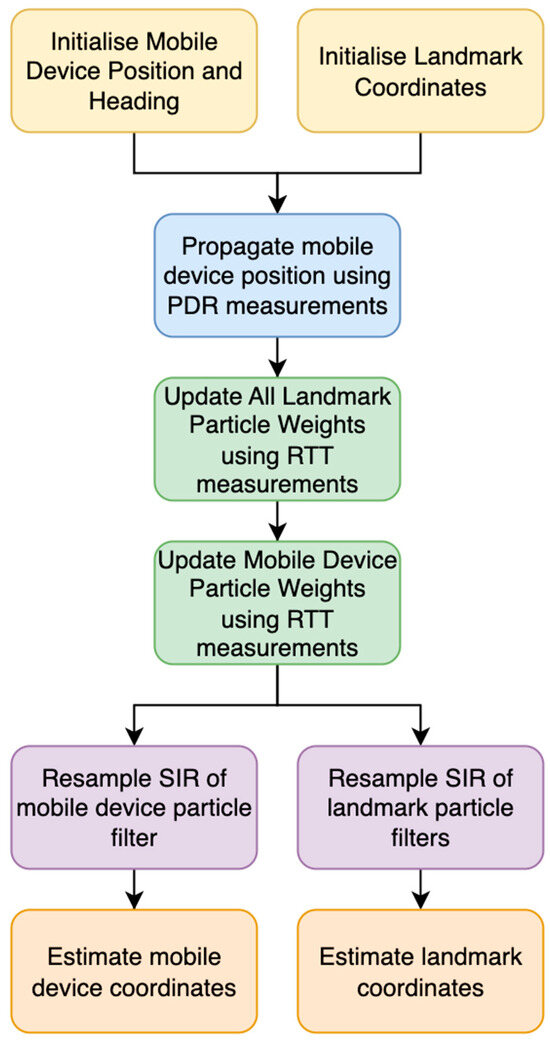
Figure 1.
FastSLAM algorithm per epoch, where each epoch is a new RTT measurement.
- The mobile device position and heading are assumed to be known. The landmark coordinates are initialised based on a uniform distribution in the environment, where each landmark will have its own particle filter.
- The PDR model is applied during the prediction step. In this step, the mobile device particles are moved according to the PDR model, with noise distributed according to a Gaussian distribution. The PDR model is described in Section 2.2.
- For the access point update step, the particles of each access point are weighted against the distance between the particle and the estimated mean coordinates of the mobile device using Equation (1). The update step for computing weightings is the step for determining how strongly a particle state matches the state suggested from measurements.
The Euclidean distance, , between each particle, j, and the landmarks is computed using Pythagoras’ theorem, where i is the AP landmark being measured from, n is the number of APs, and k represents the epoch. This distance is then treated as the mean in a Gaussian distribution, alongside a standard deviation. This standard deviation is modified using RSSI-based outlier detection, which is described in [3]. Once the Gaussian distribution is determined, the PDF of the distribution of —the measurement obtained of the distance between the AP, i, and the mobile device—is calculated using Pythagoras’ theorem at epoch k. This gives the particle weight for that landmark. The weights for all landmarks for each epoch are then multiplied together, along with the previous weight of that particle, , to give a final weight for that particle, . This process is repeated for all particles.
- 4.
- The particles of the mobile device are weighted against their distance from each estimated landmark position; the estimate is based on the mean coordinates of each landmark particle filter.
- 5.
- The particles for both the mobile device and landmarks go through sequential importance resampling (SIR) [9,10] if the particle degeneracy limit is exceeded.
- 6.
- Finally, the position estimate of the mobile device and all landmarks is calculated using the weighted average of the particle positions.
2.2. Pedestrian Dead Reckoning
The PDR model used in this paper uses the Google Android API for step detection and orientation [1] due to its convenience and also because this paper does not intend on exploring step detection models. For step length estimation, the model used in this paper is based on the Mikov step length estimation equation [11].
where q is the step length, α is a constant parameter that is calibrated per pedestrian, tstep is the time taken for a given step, fz,max is the maximum specific force along the z axis during the step, and fz,min is the minimum specific force along the z axis during the step. The mobile device was held parallel to the ground facing the direction of travel; therefore, the z axis here is perpendicular to the ground.
2.3. Experimental Setup
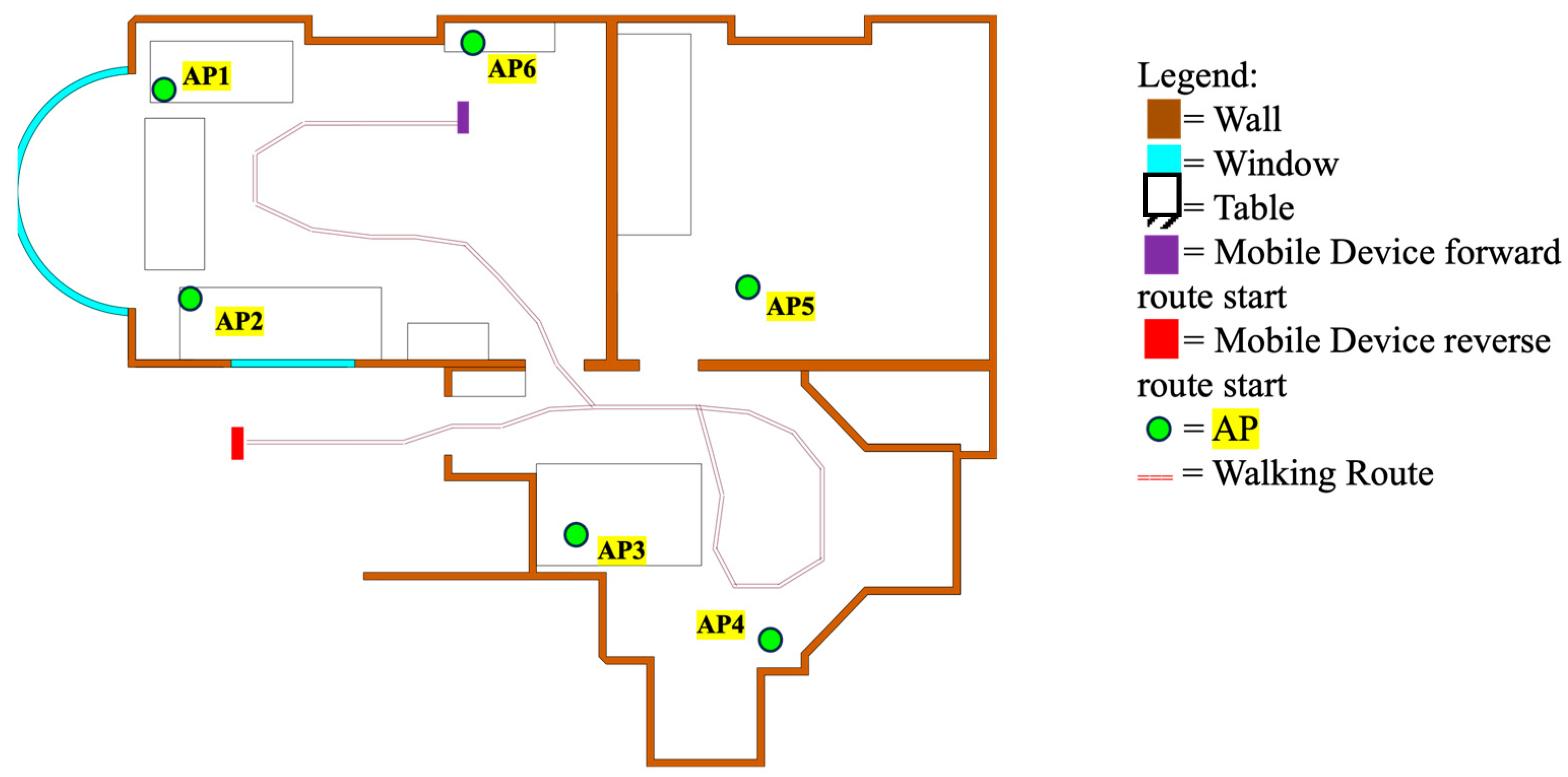
The methodology for testing the SLAM algorithm involved moving through a route in an environment in both the forward and reverse directions. These routes were designed to enable NLOS signal reception to occur. The routes and environment explored are shown in Figure 2. The trials involved a pedestrian holding the smartphone and walking on top of fixed step markers placed on the ground along the route of the trial. The markers were approximately 670 mm apart; the location of each marker was measured against the reference points in the environment to generate the step marker’s ground truth coordinates. In order to align the ground truth data with the measured data, the trials were filmed. The timestamps of the steps from the video were used to determine the expected position of a device at a given time, allowing the algorithms to have an accurate comparison point at each step. The standard deviation of the step length assuming white noise, which was used to determine the noise applied during the prediction step, was calibrated as follows. A pedestrian carrying the mobile device walks 20 steps in a straight line 10 times; the real distance travelled is measured and the estimated distance travelled is calculated using the PDR model; the standard deviation of the difference is computed, and this is divided by the number of steps to give the standard deviation of a step. All data were collected simultaneously using a custom mobile app. RTT and RSSI measurements were received at 100 ms intervals, and IMU data were collected at approximately 20 ms intervals. RSSI-based outlier detection is implemented as described by Raja and Groves [3]. A Google Pixel 4a smartphone was used in combination with 3 Google Nest WiFi Routers, a Google WiFi Router, and 2 Google WiFi Points. The fixed instrument bias for each router was calibrated out of the range estimates.
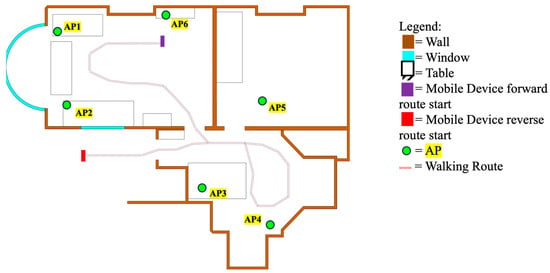
Figure 2.
Environment experimental layout.
3. Results
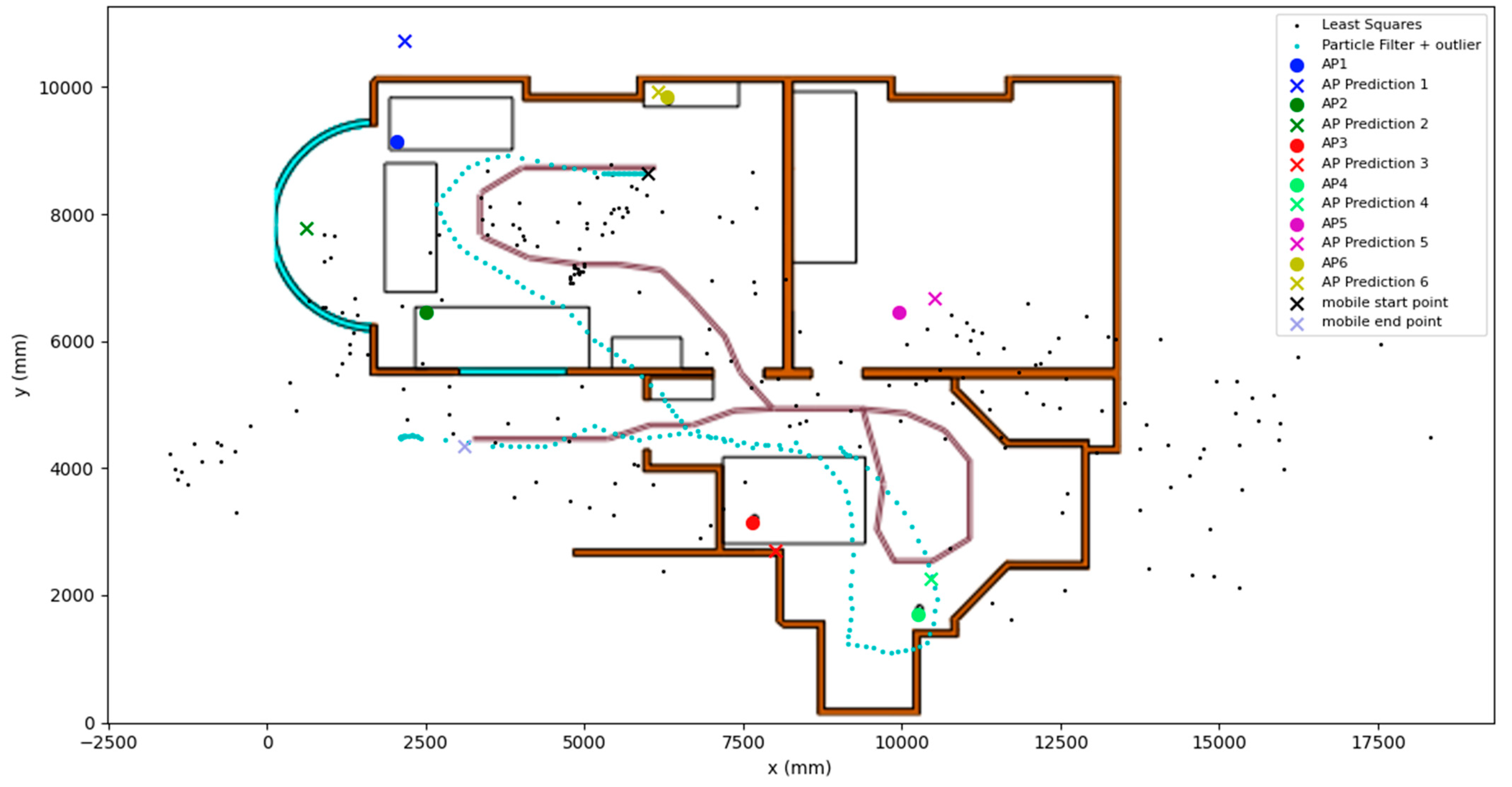
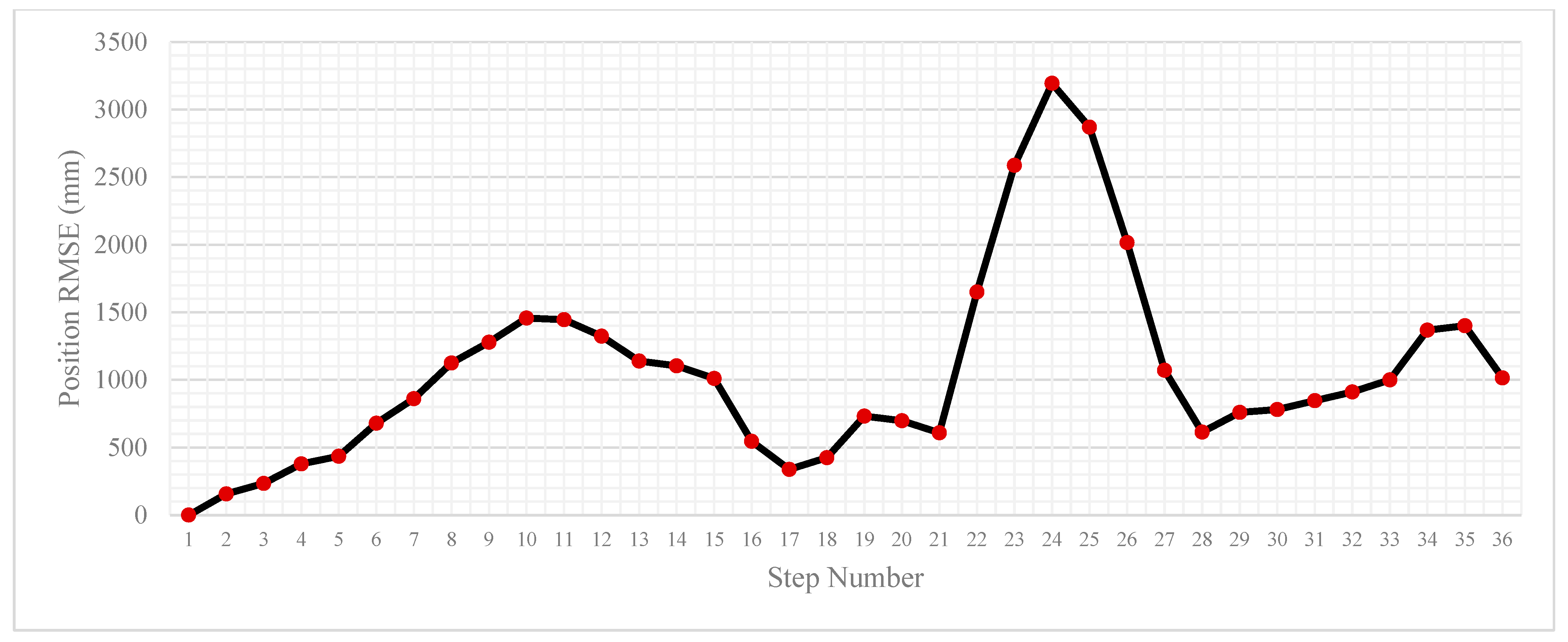
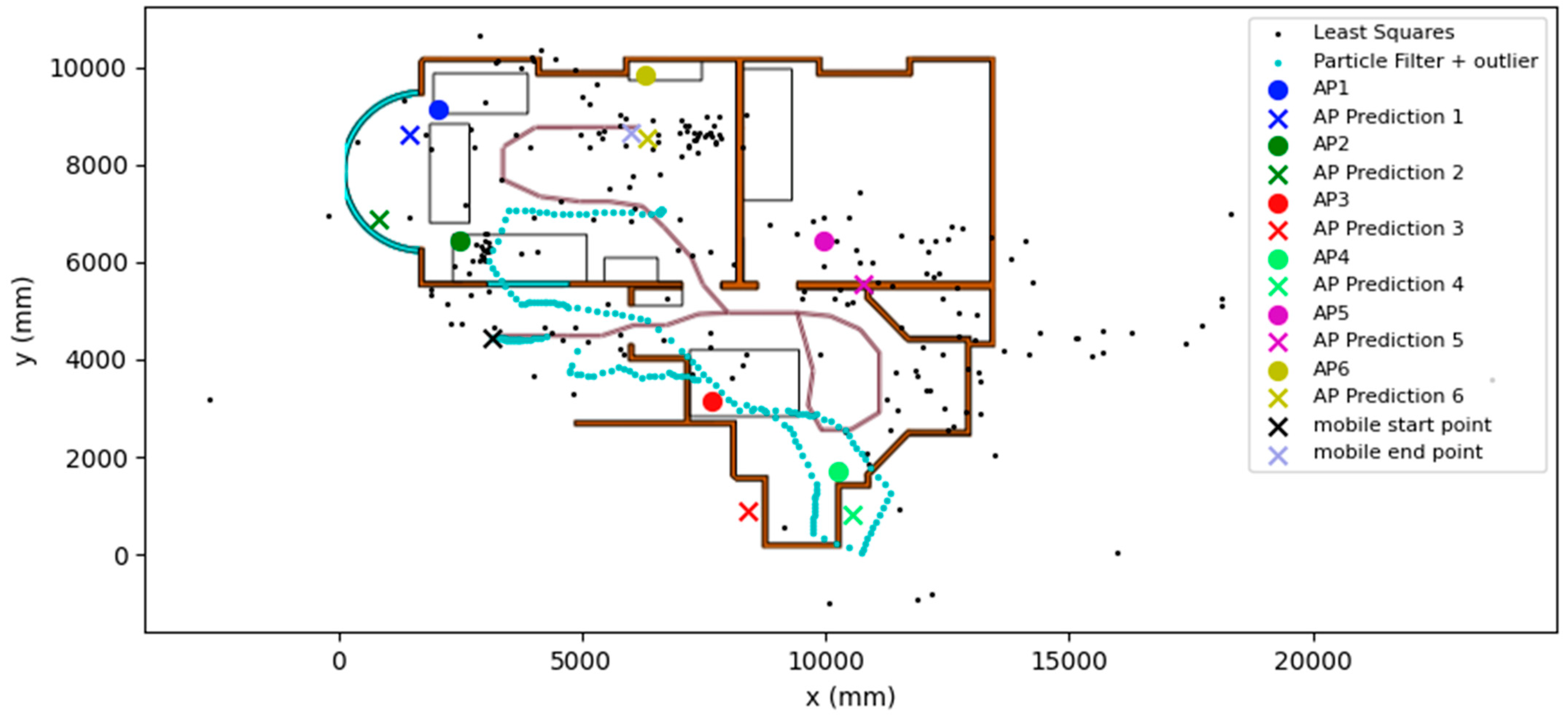
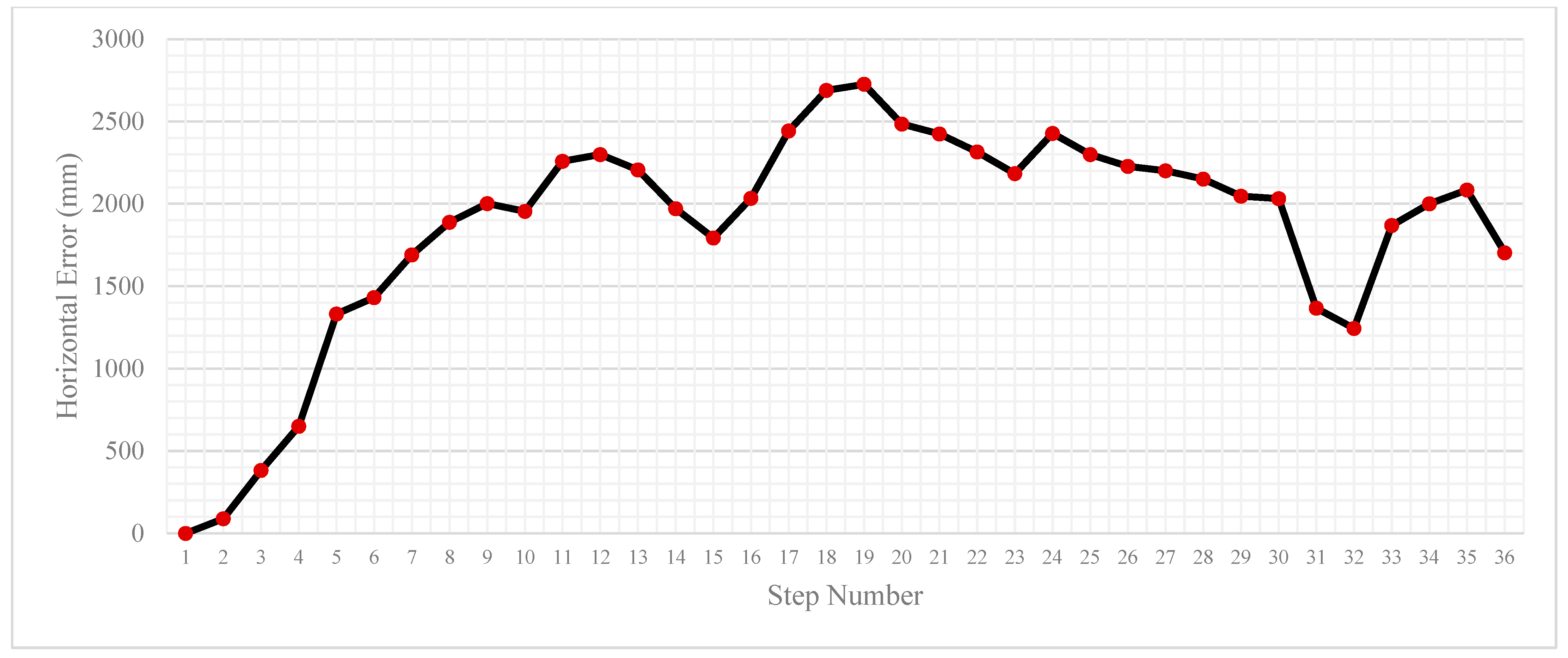
In Table 1, the statistics of the performance of the algorithm in the forward and reverse trials can be seen. Overall, the results are promising, with the mean, median, and final position RMSE for the forward trial being about a metre. The maximum horizontal error and standard deviation for the trial are 3.2 m and 0.69 m, respectively. In Figure 3 and Figure 4, during the loop section of the trial in the bottom right of the environment, the position RMSE increases by more than double. The algorithm then recovers the positioning solution to sub-metre accuracy, ending the trial at 1.01 m.

Table 1.
Statistics for the forward and reverse trials for the SLAM algorithm.
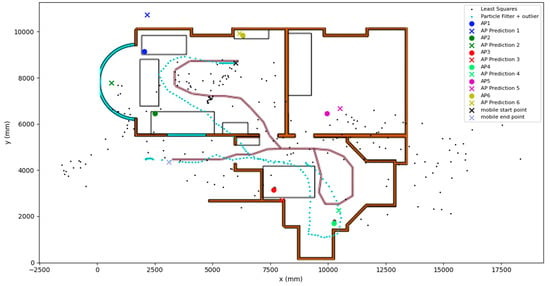
Figure 3.
Graph showing the performance of the SLAM algorithm in the forward trial.
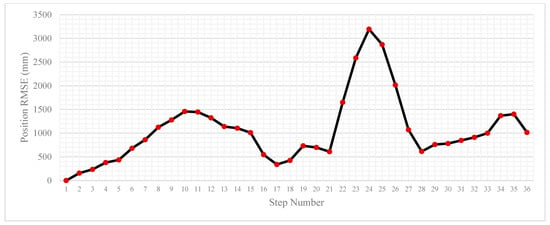
Figure 4.
Position error per step for the forward trial.
In the reverse scenario, where the mobile device begins outside and ends inside, the results are slightly worse. Firstly, in Figure 5 and Figure 6, whilst the rough shape of the predicted path of the pedestrian matches the true path, the entire path is translated down the y axis by around 2 m. The final position horizontal error is 1.7 m with an average and median horizontal error of 1.91 m and 2.03 m, respectively. This is nearly a metre worse than that of the forward trial. In the reverse scenario, the mobile device has no line of sight with any AP, whereas in the forward trial, the mobile device has a direct line of sight with three APs at the start of the trial. The lack of a line-of-sight signal will drastically reduce the reliability of the signals; thus, the overall positioning solution will be degraded with fewer line-of-sight APs. The NLOS signal reception will also have an impact on the predictions of the landmark coordinates due to the fact that in the earlier stages of the algorithm, the distance between each mobile device and the AP will be less reliable. Therefore, the starting layout of APs and the number of LOS signals plays a major role in the accuracy of the positioning solution. This is a limitation of FastSLAM in general as particle degeneracy and drift will occur with most particle-based approaches.
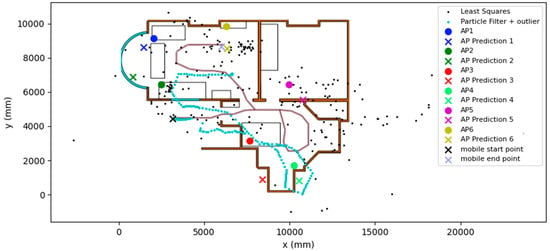
Figure 5.
Graph showing the performance of the SLAM algorithm in the reverse trial.
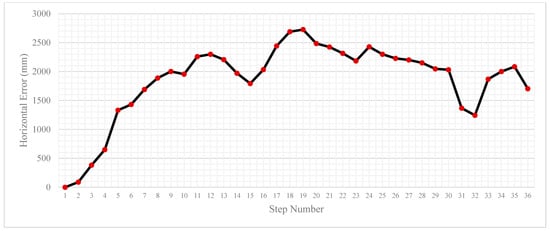
Figure 6.
Position horizontal error per step for the reverse trial.
The final landmark-estimated coordinates were also gathered and discussed here. AP6 reached a horizontal error of just 0.16 m, while AP3 reached a maximum horizontal error of 2.4 m. This is visualised in Figure 3. This demonstrates that the algorithm was able to identify the location of the landmarks to an acceptable degree of accuracy during this trial. In the forward trial, as can be seen in Figure 3, the path of the device roughly matches the shape of the true path of the pedestrian. For the reverse trial landmark final position horizontal error, the average AP final position horizontal error is 1.4 m, with the lowest position horizontal error being 0.78 m and the highest position horizontal error being 2.4 m. Interestingly, in the forward scenario, AP3 had a horizontal error of 0.58 m, and the same AP had a horizontal error of 2.4 m in the reverse scenario. This information is summarised in Table 2.

Table 2.
Statistics for the landmark position estimates.
The methodology in this paper explored a single environment with a single path walked in two directions. In order to confirm the accuracy and properly quantify the reliability of the work in this paper, a more diverse range of pedestrian walking paths, AP geometries, and indoor environments should be tested. Furthermore, the research in this paper was limited to a Google Pixel 4a and Google WiFi products; the research could benefit from testing with different mobile devices and APs.
4. Conclusions
To conclude, the SLAM algorithm is able to track the position of a pedestrian to sub-two-metre accuracy and determine the location of the landmarks to sub-two-metre accuracy 83% of the time and sub-metre accuracy 50% of the time. It was observed that when the starting position of the mobile device had access to line-of-sight signals, the location of the mobile device and the location of the landmarks could be determined to sub-metre accuracy 67% of the time. With NLOS signals, the accuracy declined, which is expected as it impacts both the location estimates of the mobile device and the access points.
Future work will include research into using prior datasets of an environment to initialise future trials, which is known as Posterity SLAM, as well as exploring other forms of cooperative SLAM. These methods should provide improvements to the accuracy and reliability of the overall positioning solution as there are more data available to determine the location of the landmarks. Finally, the research could benefit from being tested on a more diverse range of environments, mobile devices, and APs.
Author Contributions
K.J.R. is responsible for the paper. P.D.G. is the supervisor of K.J.R. and provided support with ideas for the paper, as well as providing a thorough review of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Google. Wi-Fi Location: Ranging with RTT. 2022. Available online: https://developer.android.com/guide/topics/connectivity/wifi-rtt (accessed on 2 February 2024).
- Van Diggelen, F.; Want, R.; Wang, W. How to Achieve 1-Meter Accuracy in Android. 2018. Available online: https://www.gpsworld.com/how-to-achieve-1-meter-accuracy-in-android/ (accessed on 2 February 2024).
- Raja, K.J.; Groves, P.D. WiFi-RTT Indoor Positioning Using Particle, Genetic and Grid Filters with RSSI-Based Outlier Detection. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 1644–1655. [Google Scholar]
- Gentner, C.; Ulmschneider, M.; Kuehner, I.; Dammann, A. WiFi-RTT Indoor Positioning. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1029–1035. [Google Scholar]
- Guo, G.; Chen, R.; Ye, F.; Peng, X.; Liu, Z.; Pan, Y. Indoor Smartphone Localization: A Hybrid WiFi RTT-RSS Ranging Approach. IEEE Access 2019, 7, 176767–176781. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Y.; Xu, S.; Qi, H.; Hu, X. Indoor Positioning Tightly Coupled Wi-Fi FTM Ranging and PDR Based on the Extended Kalman Filter for Smartphones. IEEE Access 2020, 8, 49671–49684. [Google Scholar] [CrossRef]
- Gentner, C.; Avram, D. WiFi-RTT-SLAM: Simultaneously Estimating the Positions of Mobile Devices and WiFiRTT Access Points. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 3142–3148. [Google Scholar] [CrossRef]
- Montemerlo, M.; Thrun, S.; Roller, D.; Wegbreit, B. FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. In Proceedings of the 18th International Joint Conference on Artificial Intelligence (IJCAI’03), Acapulco, Mexico, 9–15 August 2003; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2003; pp. 1151–1156. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans Signal Process. 2002, 50, 174–188. [Google Scholar]
- Doucet, A. University of British Columbia (no date) Importance Sampling & Sequential Importance Sampling. pp. 1–40. Available online: https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/readings/samsi_lec2.pdf (accessed on 2 February 2024).
- Mikov, A.; Moschevikin, A.; Fedorov, A.; Sikora, A. A localization system using inertial measurement units from wireless commercial hand-held devices. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard, France, 28–31 October 2013; pp. 1–7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).