Application of Quantum Computing Algorithms in the Synthesis of Control Systems for Dynamic Objects ^†

Abstract

Currently, the main focus in the automation of technological processes is on developing control systems that enhance the quality of the control process. Because the systems being controlled are often complex, multidimensional, and nonlinear, quantum computing algorithms offer an effective solution. Although there are several intelligent control methods available to improve the quality of technological processes, each has certain drawbacks. Quantum algorithms, which rely on the principles of quantum correlation and superposition, are designed to optimize control while minimizing energy and resource consumption. This article discusses the diesel fuel hydrotreating process, a critical step in oil refining. The primary goal of hydrotreating is to enhance fuel quality by removing sulfur, nitrogen, and oxygen compounds. To accurately model this process, it is essential to consider not only the external factors affecting it but also its physical characteristics. By doing so, the mathematical model becomes more precise. Based on this approach, a quantum fuzzy control system for the diesel fuel hydrotreating process was developed using quantum algorithms. These algorithms can rapidly analyze large amounts of data and make decisions. At the same time, a computer model of a fuzzy quantum control system for the process of hydrotreating diesel fuel was constructed, and a number of computational experiments were carried out. As a result, a 1.8% reduction in energy costs for the diesel fuel hydrotreating process was achieved.

1. Introduction

The automation and control of technological processes is a crucial component of modern industrial operations. As industries seek to improve productivity, efficiency, and precision, control systems have become essential in controlling dynamic processes to achieve the desired outcomes, despite disturbances from external and internal factors. However, the complexity, multidimensionality, and nonlinearity of many processes present significant challenges in control system design.

Traditional control methods, such as proportional–integral–derivative (PID) controllers and model predictive control (MPC), have been widely used in industrial settings [1]. While effective for controlling linear and moderately complex systems, these methods face limitations when applied to nonlinear, large-scale, or highly dynamic processes. Additionally, the need for real-time optimization becomes increasingly challenging as data size and complexity grow. Control system designs based on classical computing architectures are constrained by their sequential nature, limiting their ability to handle high-dimensional data in real time.

Quantum computing has emerged as a transformative technology capable of addressing complex computational problems that are beyond the capabilities of classical systems. Unlike traditional bits, which exist in binary states (0 or 1), quantum bits (qubits) can exist in multiple states simultaneously due to the principle of superposition. Furthermore, quantum entanglement enables qubits to share information instantaneously, irrespective of distance, thereby facilitating parallel computations. This allows quantum algorithms to perform certain types of computations exponentially faster than their classical counterparts, making them attractive for optimization tasks in control systems [2].

Quantum computing’s unique properties have made it a promising tool for enhancing the efficiency and performance of control systems in dynamic environments [3]. The development of quantum algorithms for optimization, such as Grover’s algorithm for search problems and the Quantum Approximate Optimization Algorithm (QAOA), has paved the way for significant advancements in control applications [4]. By enabling rapid data processing and decision-making, quantum computing offers a means to overcome the inherent limitations of classical systems when handling multidimensional data sets [5].

In control system engineering, integrating fuzzy logic with quantum computing has shown potential in managing uncertain and nonlinear systems. Fuzzy logic models human reasoning by employing linguistic variables and inference rules to handle imprecise data [6]. By incorporating quantum computing capabilities, fuzzy control systems can enhance decision-making, achieving greater precision and adaptability in real time. Quantum fuzzy control systems combine the flexibility of fuzzy logic with the computational efficiency of quantum algorithms, resulting in robust frameworks capable of optimizing control decisions under conditions of uncertainty [7,8].

This study addresses the challenges posed by complex industrial processes through the development of a quantum fuzzy control system tailored for the diesel fuel hydrotreating process. Hydrotreating is a key phase in oil refining, intended to enhance fuel quality by eliminating sulfur, nitrogen, and oxygen compounds. The process involves chemical reactions in the presence of catalysts at high temperatures and pressures, making it both resource-intensive and highly sensitive to variations in process conditions. Effective control of this process ensures compliance with regulatory standards, such as those outlined by international bodies for sulfur emissions, minimizes energy consumption, and mitigates environmental impacts. Failure to meet regulatory standards could result in operational penalties, increased production costs, and adverse environmental consequences.

The diesel fuel hydrotreating process is characterized by complex chemical kinetics and dynamic interactions between multiple variables [9]. Control parameters, including temperature, pressure, and hydrogen flow rate, must be precisely regulated to achieve optimal performance. Traditional control approaches may struggle to maintain stable process conditions when faced with external disturbances or changes in catalyst performance over time. This underscores the need for an intelligent control system capable of adapting to changing conditions while maintaining process efficiency.

The primary objective of this research is to design and evaluate a quantum fuzzy control system that optimizes the diesel fuel hydrotreating process. By leveraging the computational power of quantum algorithms, the proposed system processes large datasets to enable accurate and efficient control decisions. The integration of a quantum decision-making layer into the fuzzy logic controller enhances system performance by improving stability, adaptability to varying process conditions, and resource optimization. Unlike conventional methods that rely on static control strategies, the quantum fuzzy control system dynamically adjusts control actions based on real-time feedback.

The implementation of quantum fuzzy control systems involves the construction of a hybrid architecture that combines classical and quantum components. The classical component handles sensor data acquisition, fuzzification, and defuzzification, while the quantum component performs rapid optimization and decision-making. Quantum gates are applied to represent the possible control states, and quantum superposition enables the evaluation of multiple control scenarios simultaneously. The fuzzy inference engine generates control rules based on expert knowledge and past observations, and the quantum optimizer refines these rules to ensure optimal performance.

This research also aims to evaluate the practical feasibility of quantum fuzzy control systems in industrial settings by conducting computational experiments and simulations. A key focus is the comparison of energy consumption, impurity reduction, and control stability between the proposed system and conventional control methods. Preliminary results indicate that quantum fuzzy control systems can achieve significant improvements in energy efficiency and process stability, contributing to a reduction in overall production costs.

2. Methodology

Quantum computing methods are based on the principle of quantum superposition. In a quantum computing scheme, these two states $(|0⟩$ and $(|1⟩$ can exist in a superposition state, meaning that the most general state of a quantum bit can be written as follows:

$$|\Psi ⟩=\alpha |0⟩+\beta |1⟩$$

(1)

where $\alpha$ and $\beta$ are a complex numbers.

To represent the two states of qubits, the bra $(⟨ |$ and ket $(| ⟩$ notations from Dirac notation are used. Vectors in the form of $(| ⟩$ are called ket-vectors, while vectors in the form of $(⟨ |$ are called bra-vectors. The ket notation corresponds to the following vectors: (a) the ket-vector corresponding to zero; (b) the ket-vector representing the one state of the qubit:

$$|0⟩=\left[\begin{array}{c}1\\ 0\end{array}\right] \mathrm{and} |1⟩=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

(2)

When measuring the system’s state using function $|\Psi ⟩=\alpha |0⟩+\beta |1⟩$, the probability of detecting it in the $|0⟩$ state is ${\alpha }^2$, and the probability of detecting it in the $(⟨1|$ state is ${\beta }^2$. The sum of these probabilities must be equal to one, which is known as the normalization condition [10]:

$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$$

(3)

This relationship is called the normalization condition.

Quantum computing typically requires more than one qubit. A system composed of multiple qubits embodies the tensor product of its constituent subsystems. Such a system is called a quantum system.

The state of an n-qubit quantum system can be expressed using the following mathematical relationship:

$$|q_1⟩\dots |q_n⟩=\left({\alpha }_0\right|0⟩+{\beta }_0|1⟩⨂({\alpha }_1\left|0⟩+{\beta }_1\right|1⟩⨂\dots ⨂\left({\alpha }_{n-1}\left|0⟩+{\beta }_{n-1}\right|1⟩\right)$$

The complete mixed state of a two-qubit system can be described as follows:

$$|\psi ⟩=({\alpha }_0|0⟩+{\beta }_0|1⟩⨂({\alpha }_1\left|0⟩+{\beta }_1\right|1⟩={\alpha }_0{\alpha }_1|00⟩+{\alpha }_0{\beta }_1|01⟩+{\beta }_0{\alpha }_1|10⟩+{\beta }_0{\beta }_1|11⟩$$

To create superposition states, the Hadamard (H) operator is used. The Hadamard operator in matrix form is represented as [11]

$$H={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$$

(4)

Qubit states can be expressed mathematically as follows:

$$|0⟩=\left(\begin{array}{c}1\\ 0\end{array}\right); |1⟩=\left(\begin{array}{c}0\\ 1\end{array}\right); |\Psi ⟩=\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)$$

(5)

The key features of quantum computing methods lie in their ability to consider the natural properties of nonlinear objects when solving synthesis problems and to establish new control laws.

The possibilities of using quantum computing methods for controlling the hydrotreatment process of diesel fuel, which exhibits nonlinear characteristics, have been explored.

The mathematical model of the diesel fuel hydrotreatment process consists of three main components. The material balance equation describes the change in concentration of sulfur-containing compounds and other reactants in the reactor volume over time. This equation ensures that the total inflow of reactants into the system balances with the reaction consumption and the outlet flow of the products [12]. It is expressed as

$${\displaystyle \frac{d{C}_A}{dt}}={\displaystyle \frac{F}{V}}·\left(C_{A0}-C_A\right)+r$$

(6)

where $C_A$ is a concentration of aromatic compounds (mole/L), $C_{A0}$ is an initial concentration of aromatic compounds (mole/L), $F$ is the volumetric flow of diesel fuel (${\mathrm{m}}^3/\mathrm{s}),$ $V$ is the volume of the reactor (m³), and $r$ is reaction rate ($\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}/\mathrm{L}·\mathrm{s})$.

The reaction rate equation accounts for the transformation of sulfur-containing compounds when they react with hydrogen in the presence of a catalyst to form hydrogen sulfide (H₂S) and desulfurized hydrocarbons [13]. The reaction rate is given as

$$r=k_f·C_A·C_H-k_r·C_{AS},$$

(7)

where $k_f$ and $k_r$ are the rate constants of the forward and reverse reactions depend on temperature. This equation follows the Langmuir–Hinshelwood mechanism, which considers catalyst surface adsorption effects.

The heat balance equation describes the temperature changes in the reactor due to reaction heat, heat loss, and energy transfer by the hydrogen gas stream. The equation is formulated as

$$\rho ·c_p·{\displaystyle \frac{dT}{dt}}={\displaystyle \frac{F}{V}}·\left(T_0-T\right)+∆H·r-Q_q$$

(8)

where $T$ is the temperature of reactor (K), $T_0$ is the temperature of inlet flow, $∆H$ is the thermal effect of the reaction (J/mole), and $Q_q$ is heat transferred by hydrogen (J).

The process is highly sensitive to temperature fluctuations, making precise thermal control essential for maintaining optimal reactor performance. The reaction rate constants are determined using the Arrhenius equation, which expresses the temperature dependence of the reaction kinetics as

$$k_f=k_{f0}·exp\left(-{\displaystyle \frac{E_f}{R·T}}\right), k_r=k_{r0}·exp\left(-{\displaystyle \frac{E_r}{R·T}}\right),$$

(9)

where $k_{f0}, k_{r0}$ are pre-exponential factors, $E_f$, $E_r$ are activation energies, and $R$ is the universal gas constant (8.314 J/(mol·K)).

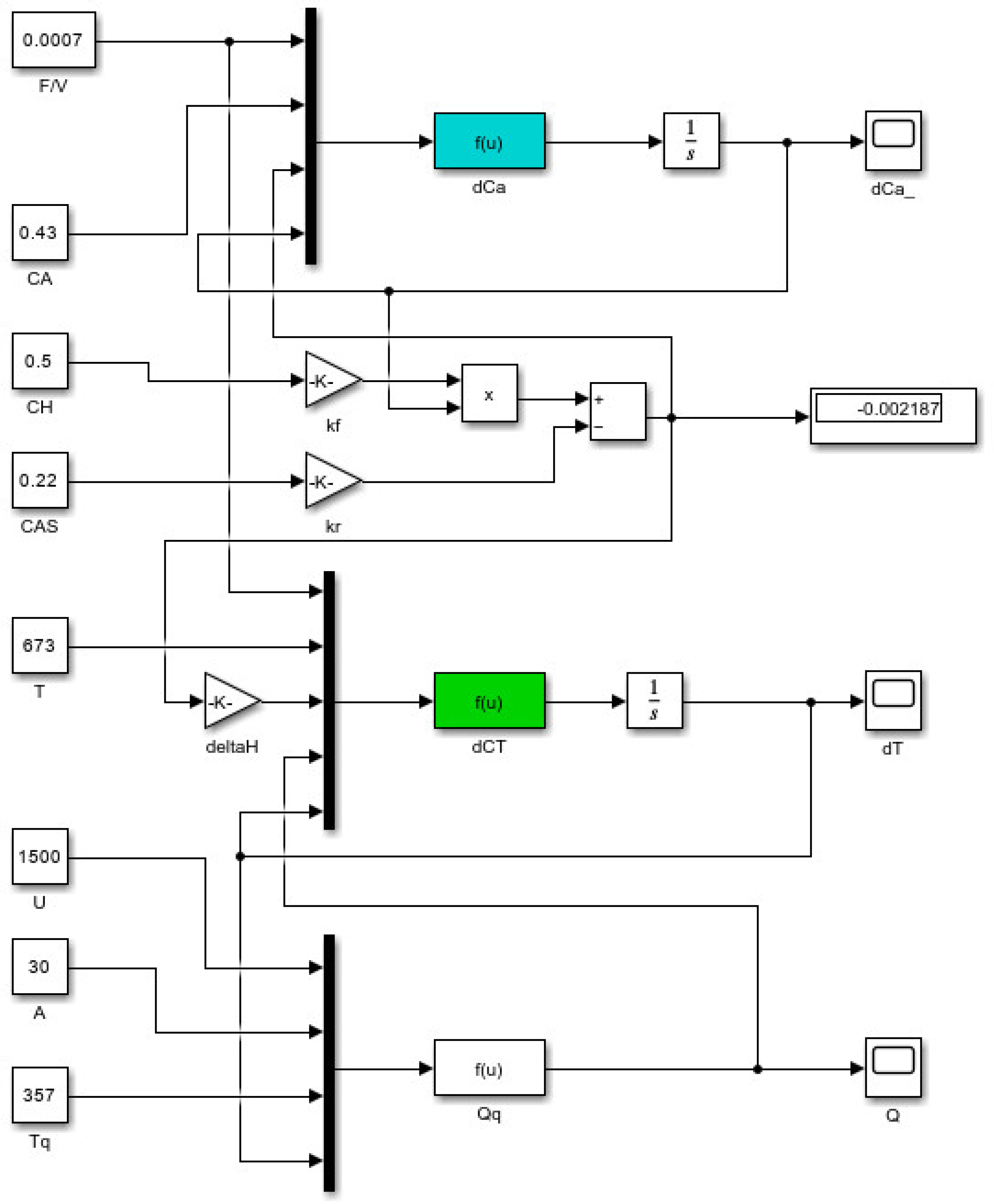
The MATLAB R2024b software package was used to implement the mathematical model of the hydrotreatment process [14,15]. A block diagram of the MATLAB model is shown in Figure 1, which represents the computational structure of the hydrotreatment process.

In this study, the quantum controlling method is realized by integrating a quantum decision-making module within the fuzzy inference system. The design is based on the Quantum Approximate Optimization Algorithm, which utilizes quantum circuits to search for near-optimal solutions in a discrete optimization space. The fuzzy rules, initially derived from expert knowledge and empirical process data, are encoded as quantum states. These states are manipulated using unitary transformations—represented by a combination of Hadamard, phase, and controlled-NOT (CNOT) gates—to explore multiple control trajectories simultaneously via quantum superposition.

A critical aspect of the quantum controller is its ability to handle uncertainty and nonlinearity in real time. The quantum layer calculates the expected values of different control scenarios by applying measurement operators on the quantum state vector. These expected values represent the cost function—typically energy consumption or impurity levels—which the system seeks to minimize. The outcome of the quantum computation guides the defuzzification process to produce crisp control actions that adapt dynamically to the process environment.

The hybrid quantum–classical control structure proposed in this study is illustrated in Figure 2, which demonstrates the interaction between traditional PID control, quantum algorithms (QA), and neural network-based modules (NNC1 and NNC2). This architecture combines the robustness of classical control with the adaptability and optimization power of quantum-enhanced computation.

Figure 2 presents a functional structure where the quantum-enhanced controller operates in tandem with a conventional PID controller. The quantum control architecture includes two neural network components, NNC1 and NNC2, which receive process feedback and output signals. These neural networks assist in tuning the quantum algorithm block that generates optimal control actions based on a pre-established knowledge base.

The quantum algorithm (QA) block serves as the optimization core of the system. It interprets current and historical process states (processed by NNC1 and NNC2) to refine the control signal dynamically. This results in adaptive PID gains that adjust in real time depending on system behavior, thereby enhancing control stability and response speed. The output of the QA is then fed into a classical PID controller that determines the control action applied to the Control Object—in this case, the diesel fuel hydrotreating process. The Measurement System continuously captures real-time process parameters m(t), and a delay block Z⁻¹ is used to maintain historical state awareness for quantum optimization. A feedback loop ensures that the control action is evaluated and corrected continuously, and the updated control status is reflected on the device.

In the next stage, the control system elements are integrated into the developed model of the process. The block diagram of the control system model in SIMULINK is shown in Figure 3. This block diagram integrates the previously developed process model with the controller, represented as quantum computing algorithms.

3. Result and Discussion

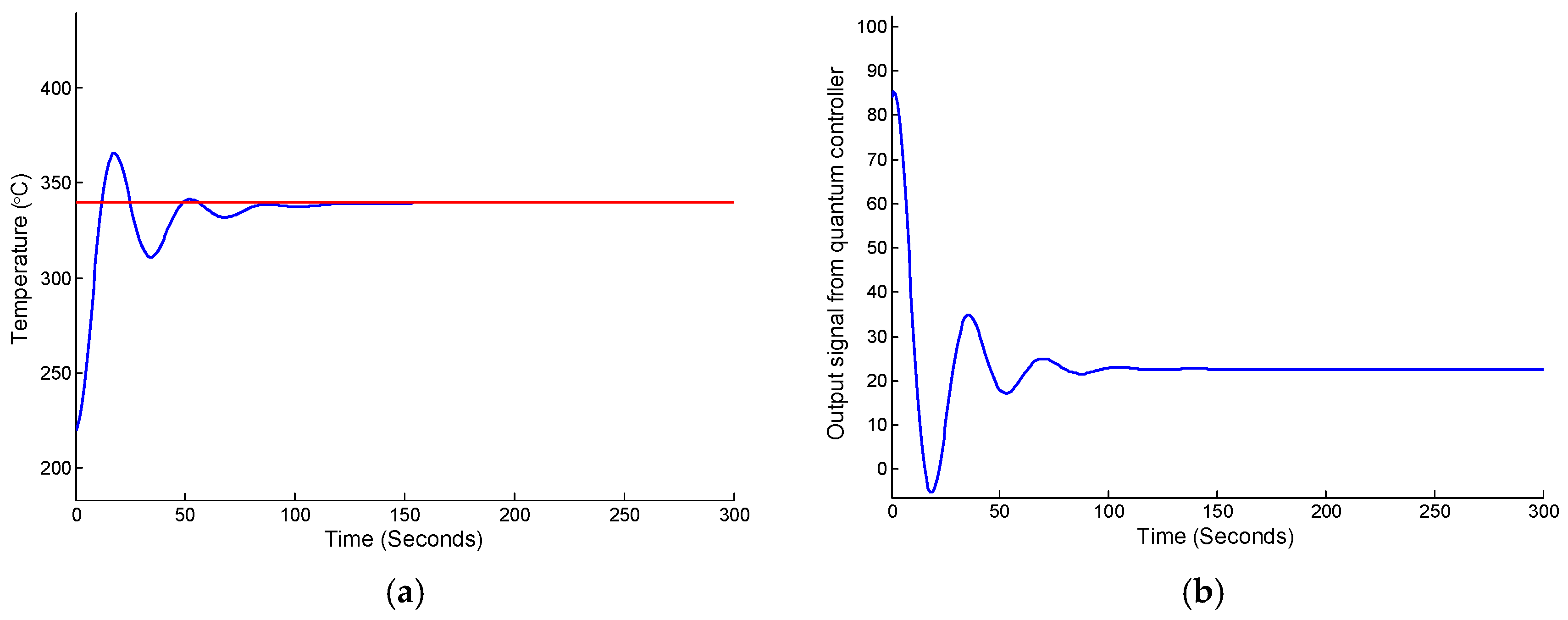
The results of the simulation and computational experiments conducted on the quantum fuzzy control system for the diesel fuel hydrotreatment process demonstrate significant improvements in process efficiency, stability, and product quality. Figure 4a illustrates the transient characteristics of the output parameters, showing the temperature changes over time. The quantum controller effectively maintained the reactor temperature within the optimal range, demonstrating high stability despite external disturbances. Figure 4b depicts the output signal of the quantum controller during temperature control, which highlights its rapid response and adaptability to changing process conditions.

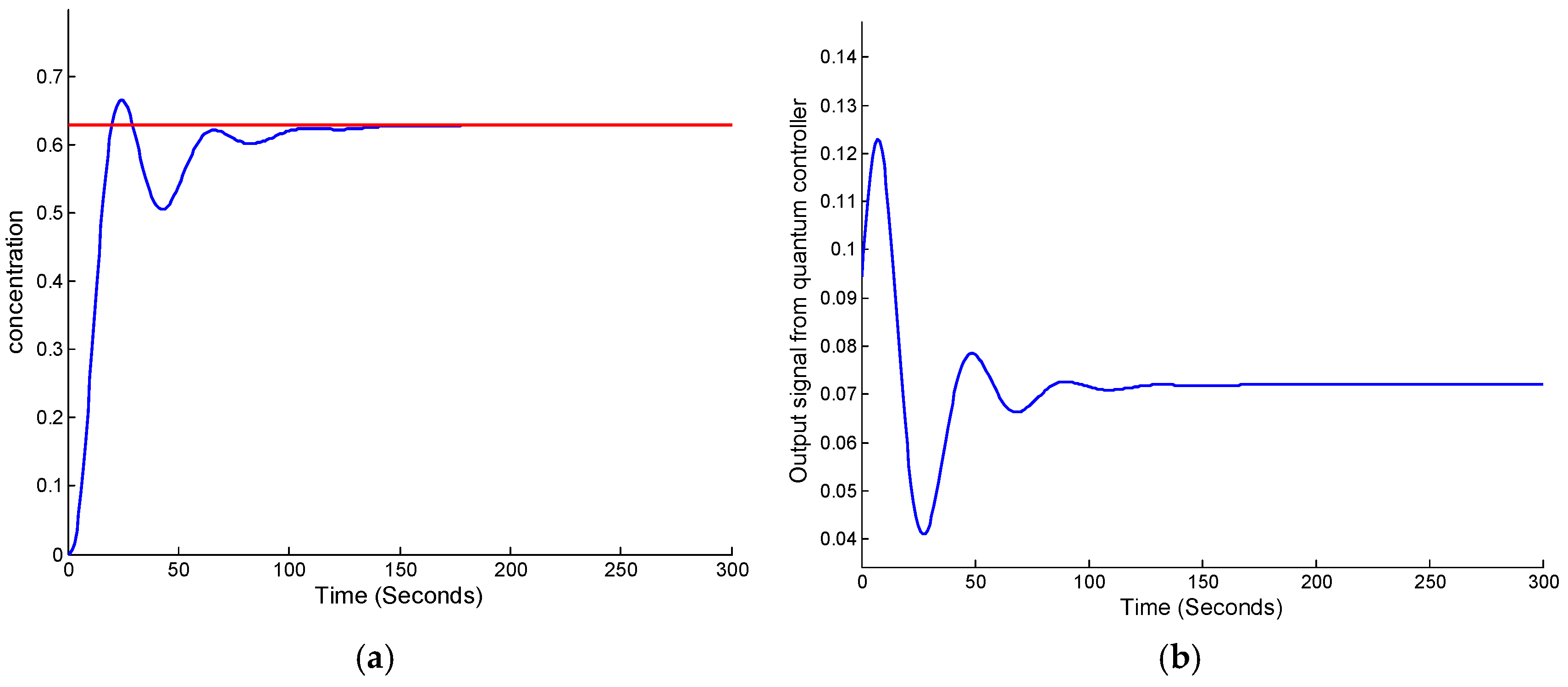
Similarly, Figure 5a shows the transient characteristics of the concentration of sulfur-containing compounds, where the quantum fuzzy control system ensured efficient removal of sulfur compounds and maintained concentrations within desired thresholds. Figure 5b further depicts the corresponding quantum controller output signal for concentration control, showcasing the controller’s capability to dynamically adjust its decisions in real time.

The purified diesel fuel and byproduct compositions obtained from the simulation are summarized in

Table 1. Simulation results.

Product % Mass	Experiment
Purified fraction of diesel fuel	95.0
Hydrogen sulfide	0.148
Water	0.1
Ammonia	0.03
Petrol	1.022
Hydrocarbon gas	3.1
The remaining sulfur composition	0.63

. The results indicate that the quantum fuzzy control system achieved a 95% yield of purified diesel fuel while significantly reducing impurities such as sulfur, hydrogen sulfide, and ammonia.

The developed mathematical models and quantum fuzzy control system demonstrated several key benefits in optimizing the hydrotreatment process. The hydrogen consumption was significantly reduced, lowering operational costs. Additionally, the production of purified diesel fuel increased, maximizing process efficiency. There was also a noticeable decrease in the quantity of fine crystal particles in the purified fuel, enhancing its quality. Furthermore, the quantum fuzzy control system resulted in a 1.8% reduction in energy consumption compared to conventional control systems, underscoring its potential for improving energy efficiency in industrial applications.

4. Conclusions

This study investigates the diesel fuel hydrotreatment process using a computational model implemented in MATLAB. The hydrotreatment process is a nonlinear chemical system involving complex interactions between chemical kinetics, mass transfer, and heat transfer phenomena. The primary objective of this study was to model and analyze the influence of key process parameters such as temperature, reaction rate, and hydrogen concentration on the desulfurization efficiency of diesel fuel. Also, a quantum control system was employed to achieve optimal control of diesel hydro treatment process.

Any real object is characterized by nonlinearity, multi-dimensionality, and multiple interconnections, where various modes and complex transient processes occur. Creating a control system for such objects that fully considers their nonlinearity across a wide range can achieve high efficiency through the use of quantum computing methods. Quantum control methods allow for the consideration of the nonlinear properties and multi-dimensional interconnections of the process, enabling the formulation of new control laws. By using this approach, the efficiency of controlling key parameters in the hydro treatment process—such as reactor temperature, hydrogen concentration, and reaction rate—was significantly improved. The quantum control system works in conjunction with mathematical models to determine the optimal operating points of the hydro treatment process and ensure the best operating conditions. This approach not only enhances energy efficiency and product quality but also minimizes the costs associated with resources such as hydrogen and catalysts.

This study developed a quantum fuzzy control system for diesel fuel hydrotreatment, significantly improving process stability, efficiency, and energy consumption. The system effectively managed nonlinear dynamics, optimizing key parameters such as temperature, hydrogen concentration, and sulfur removal.

Simulation results showed a 95% yield of purified diesel fuel, with reduced sulfur and impurities, ensuring higher product quality and compliance with environmental standards. The quantum control system achieved 1.8% lower energy consumption, optimizing hydrogen and catalyst use while reducing operational costs.

Leveraging quantum superposition and entanglement, the system enabled real-time optimization, outperforming traditional control methods in computational efficiency. These findings highlight the potential of quantum fuzzy control systems to revolutionize process automation, making operations more sustainable and cost-effective. Future research should focus on further refinements and real-world implementation.