Comparative Study of Propeller Thrust Force on Unmanned Aerial Vehicle Using Ground Testing Methods and Theoretical Calculations †
Abstract
1. Introduction
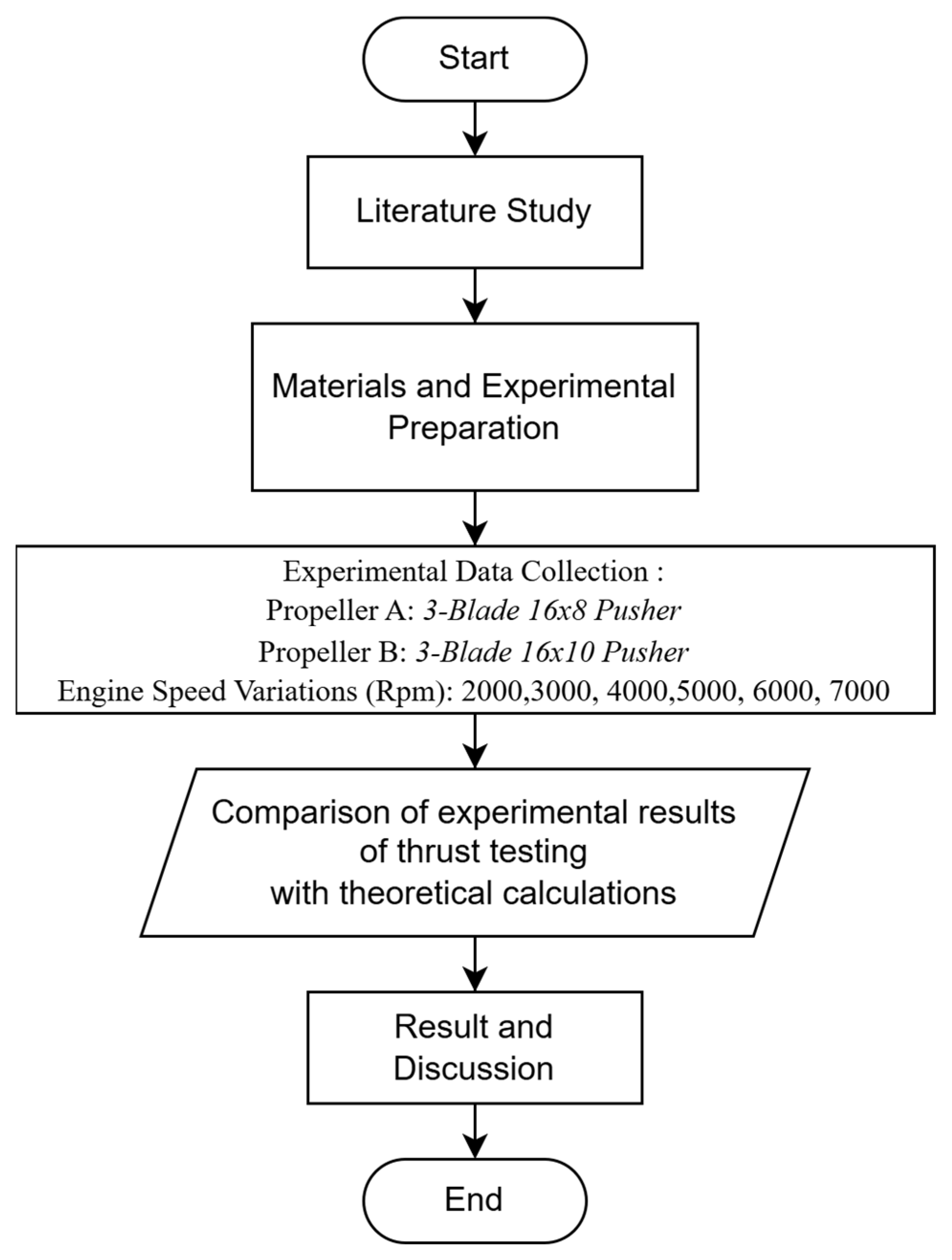
2. Materials and Methods
2.1. Ground Test Bed
2.2. Theoretical Calculation
3. Result and Discussion
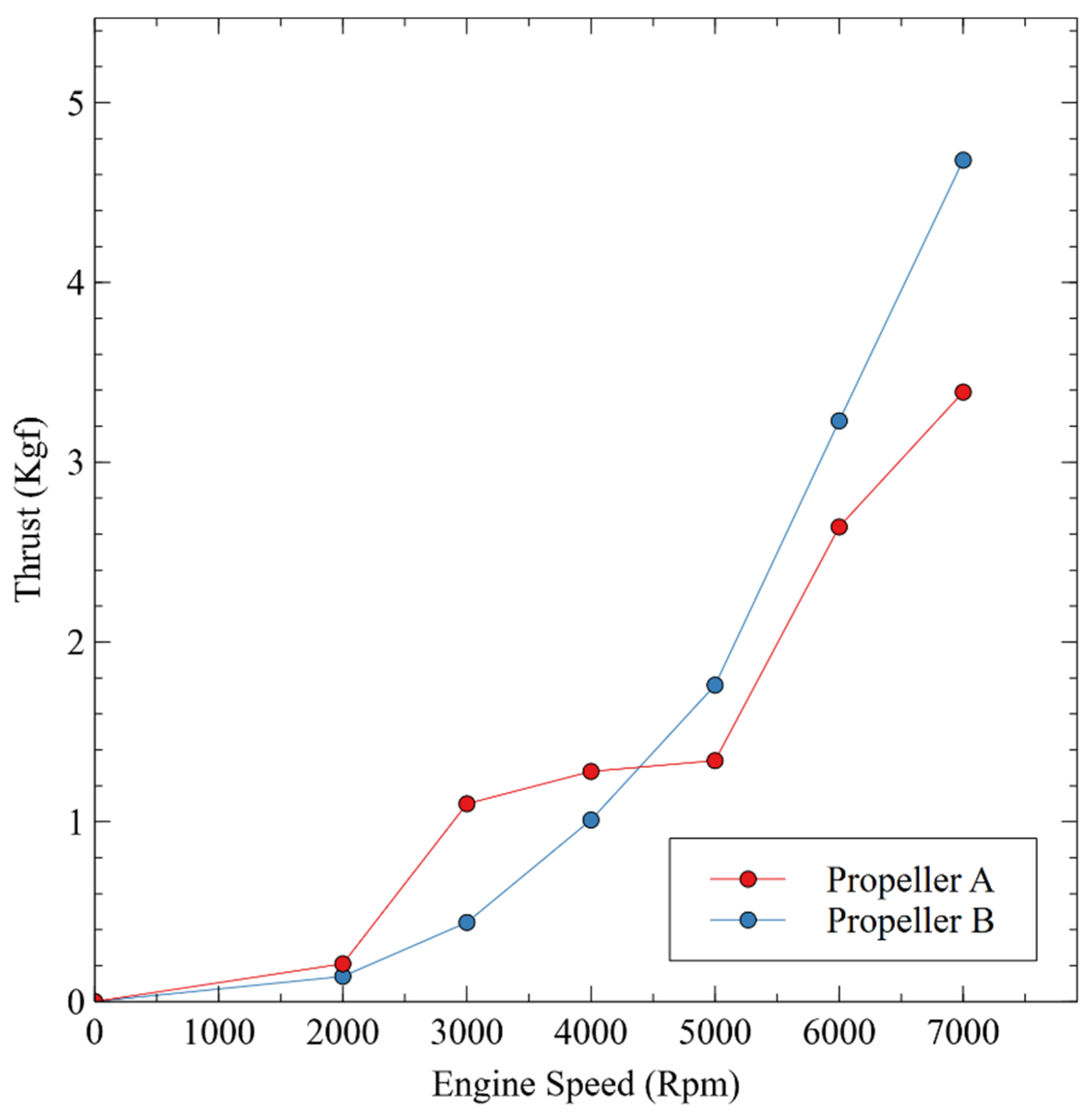
3.1. Experimental Result
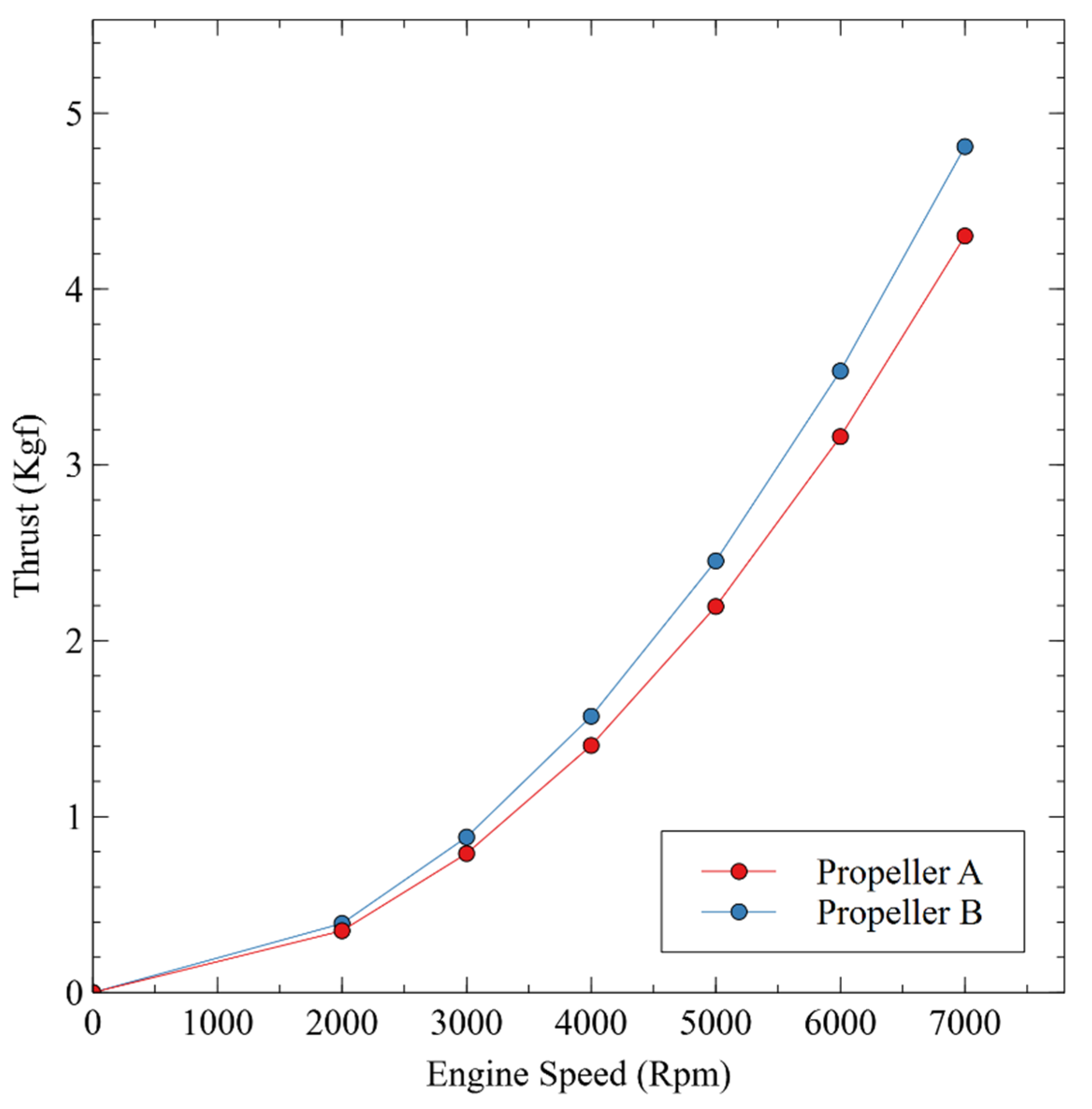
3.2. Theoretical Calculation Result
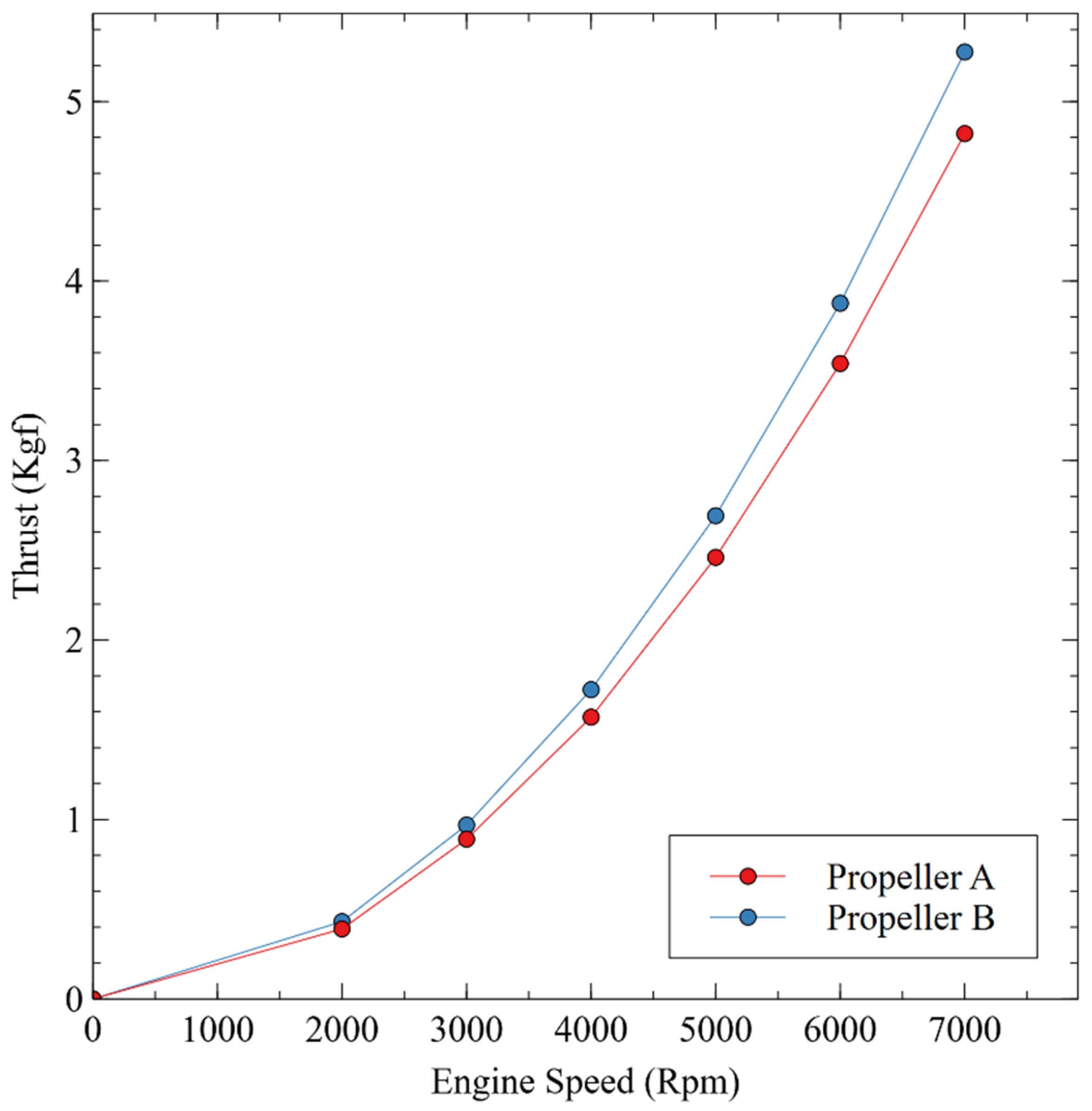
3.3. Propeller Power Calculator Result
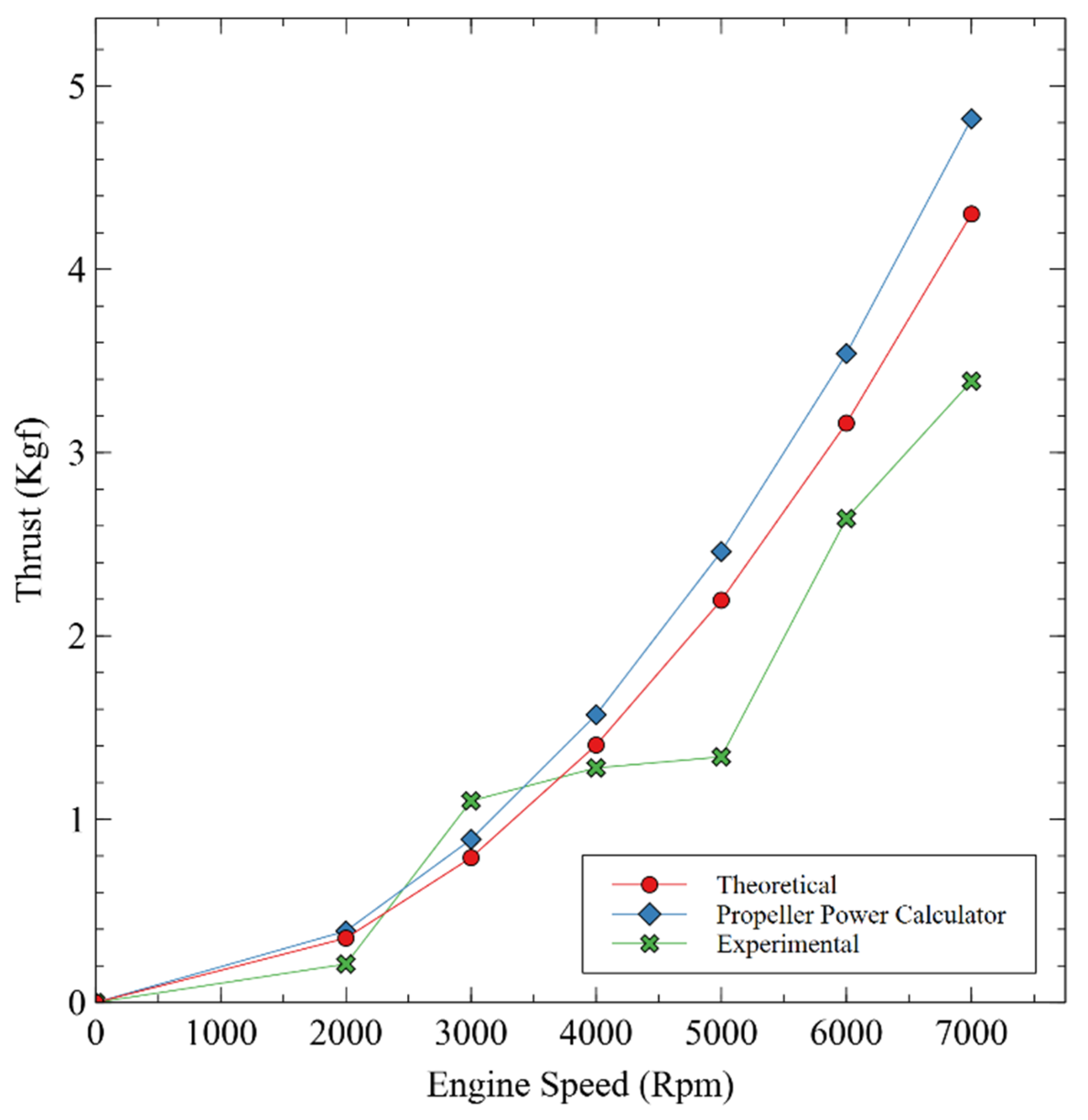
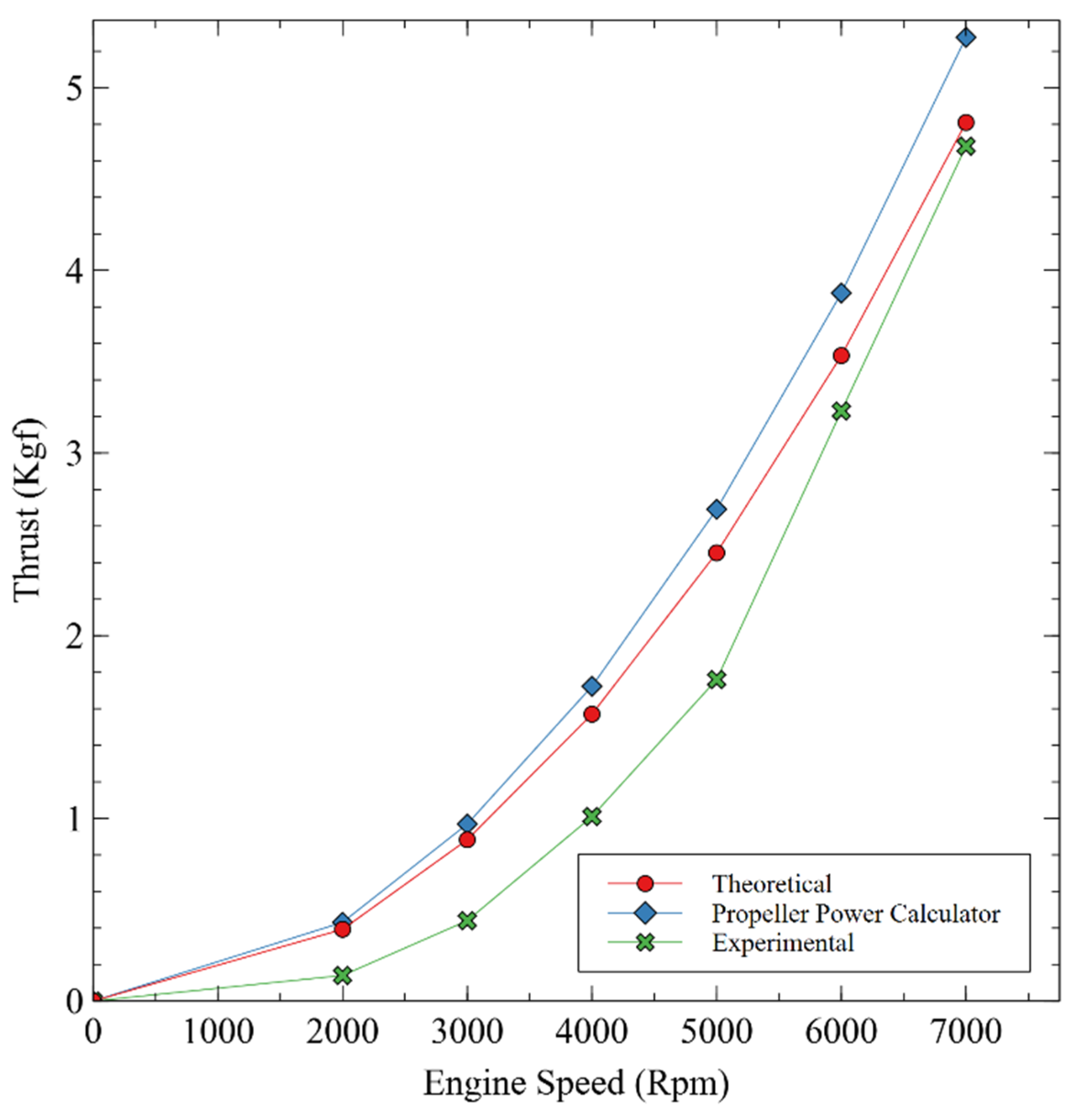
3.4. Comparison of Experimental, Theoretical, and Propeller Power Calculator Results
4. Conclusions
- From the experimental results, the thrust produced increases along with the increase in engine speed on both types of propellers. The lowest thrust is produced at 2000 Rpm, which is 0.21 Kgf and 0.14 Kgf, respectively, for propellers A and B. The highest thrust is produced at 7000 Rpm, which is 3.39 Kgf and 4.68 Kgf, respectively, for propellers A and B.
- The theoretical calculation indicates that thrust production increases with the rise in engine speed for both propeller designs. The minimum thrust occurs at 2000 RPM, providing 0.390 Kgf for propeller A and 0.431 Kgf for propeller B. The maximum thrust occurs at 7000 RPM, measuring 4.821 Kgf for propeller A and 5.276 Kgf for propeller B. The data indicate that propeller B outperforms propeller A in generating thrust force at engine speeds ranging from 2000 to 7000 RPM. This result aligns with the findings from the propeller power calculator.
- The practical and theoretical comparisons indicate that propeller B exceeds propeller A. The thrust generated at each engine speed indicates that propeller B produces more thrust force. However, an exception exists in the experimental data at low RPM, where propeller A exhibits a higher trend than propeller B. This results from many characteristics that enable propeller A to outperform propeller B at low RPM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elmeseiry, N.; Alshaer, N.; Ismail, T. A Detailed Survey and Future Directions of Unmanned Aerial Vehicles (UAVs) with Potential Applications. Aerospace 2021, 8, 363. [Google Scholar] [CrossRef]
- Andria, G.; Di Nisio, A.; Lanzolla, A.; Spadevecchia, M.; Pascazio, G.; Antonacci, F.; Sorrentino, G. Design and Performance Evaluation of Drone Propellers. In Proceedings of the 2018 5th IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Rome, Italy, 20–22 June 2018; pp. 407–412. [Google Scholar]
- Ilham, K.; Mukhaiyar, R. Pergerakan Autonomous Pesawat Tanpa Awak Berdasarkan Tinggi Terbang Pesawat. Ranah Res. J. Multidiscip. Res. Dev. 2021, 3, 154–165. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Prakken, E. Design, Modeling, and Control of a Novel Multirotor UAV with Embedded 3D-Printed Thrust Force Sensor. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- MacNeill, R.; Verstraete, D.; Gong, A. Optimisation of Propellers for UAV Powertrains. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; p. 5090. [Google Scholar]
- Sihaan, J.C.R.; Munawir, A.; Husin, Z. Analisis Gaya Dorong (Thrust) Propeller Pada Pesawat Model Remote Control (Uav). J. Mekanova Mek. Inov. Dan Teknol. 2022, 8, 135–142. [Google Scholar] [CrossRef]
- Augustiantyo, B.; Setiawan, R. Optimasi Desain Bilah Dengan Metode Linearisasi Chord Dan Twist Terhadap Performa Turbin Angin Sumbu Horizontal. Media Mesin Maj. Tek. Mesin 2021, 22, 97–110. [Google Scholar] [CrossRef]
- Pribadyo, P.; Hadiyanto, H.; Jamari, J. Simulasi Performa Turbin Propeller Dengan Sudut Pitch Yang Divariasikan. J. Mekanova Mek. Inov. Dan Teknol. 2020, 6, 54–63. [Google Scholar] [CrossRef]
- Sarjito; Aklis, N.; Hartanto, T. An Optimization of Flap and Slat Angle Airfoil NACA 2410 Using CFD. AIP Conf. Proc. 2017, 1831, 020038. [Google Scholar] [CrossRef]
- Hartanto, T.; Sarjito, I.; Nur Aklis, S. Analisa Aerodinamika Flap Dan Slat Pada Airfoil NACA 2410 Terhadap Koefisien Lift Dan Koefisien Drag Dengan Metode Computational Fluid Dynamic. Ph.D. Dissertation, Universitas Muhammadiyah Surakarta, Surakarta, Jawa Tengah, Indonesia, 2015. [Google Scholar]
- Perdana, D.W.A.; Effendy, M. Studi Numerik Dan Eksperimen Aerodinamika Airfoil NACA 24112. Creat. Res. Eng. (CERIE) 2021, 1, 1–11. [Google Scholar] [CrossRef]
- Mohamed, W.M.W.; Ravindran, N.P.; Rajendran, P. A CFD Simulation on the Performance of Slotted Propeller Design for Various Airfoil Configurations. CFD Lett. 2021, 13, 43–57. [Google Scholar] [CrossRef]
- OS Engine OS GT-33 Piston Engine Specifications 2024. Available online: https://www.os-engines.co.jp/english/line_up/engine/air/aircraft/img/manual/38300.pdf (accessed on 22 August 2024).
- Shen, C.H.; Albert, F.; Ang, C.; Teck, D.J.; Chan, K. Theoretical Development and Study of Takeoff Constraint Thrust Equation for a Drone. In Proceedings of the 2017 IEEE 15th Student Conference on Research and Development (SCOReD), Wilayah Persekutuan Putrajaya, Malaysia, 13–14 December 2017; pp. 18–22. [Google Scholar]
- Wald, Q.R. The Aerodynamics of Propellers. Prog. Aerosp. Sci. 2006, 42, 85–128. [Google Scholar] [CrossRef]
- Stapples, G. Propeller Static & Dynamic Thrust Calculation. 2014, Volume 1, pp. 1–2. Available online: https://www.electricrcaircraftguy.com/2013/09/propeller-static-dynamic-thrust-equation.html (accessed on 10 December 2024).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faishal, A.; Setyadewi, I.T.; Aklis, N.; Harjanto, F.; Wibowo, A.M.; Supriyanto, A. Comparative Study of Propeller Thrust Force on Unmanned Aerial Vehicle Using Ground Testing Methods and Theoretical Calculations. Eng. Proc. 2025, 84, 59. https://doi.org/10.3390/engproc2025084059
Faishal A, Setyadewi IT, Aklis N, Harjanto F, Wibowo AM, Supriyanto A. Comparative Study of Propeller Thrust Force on Unmanned Aerial Vehicle Using Ground Testing Methods and Theoretical Calculations. Engineering Proceedings. 2025; 84(1):59. https://doi.org/10.3390/engproc2025084059
Chicago/Turabian StyleFaishal, Afif, Imas Tri Setyadewi, Nur Aklis, Furqaan Harjanto, Ari Mukti Wibowo, and Agung Supriyanto. 2025. "Comparative Study of Propeller Thrust Force on Unmanned Aerial Vehicle Using Ground Testing Methods and Theoretical Calculations" Engineering Proceedings 84, no. 1: 59. https://doi.org/10.3390/engproc2025084059
APA StyleFaishal, A., Setyadewi, I. T., Aklis, N., Harjanto, F., Wibowo, A. M., & Supriyanto, A. (2025). Comparative Study of Propeller Thrust Force on Unmanned Aerial Vehicle Using Ground Testing Methods and Theoretical Calculations. Engineering Proceedings, 84(1), 59. https://doi.org/10.3390/engproc2025084059





