Transformation of Guided Ultrasonic Wave Signals from Air Coupled to Surface Bounded Measurement Systems with Machine Learning Algorithms for Training Data Augmentation †
Abstract
1. Introduction
2. Methods and Experiments
2.1. Experimental Setup
2.2. Data Preprocessing
2.3. Machine Learning Models
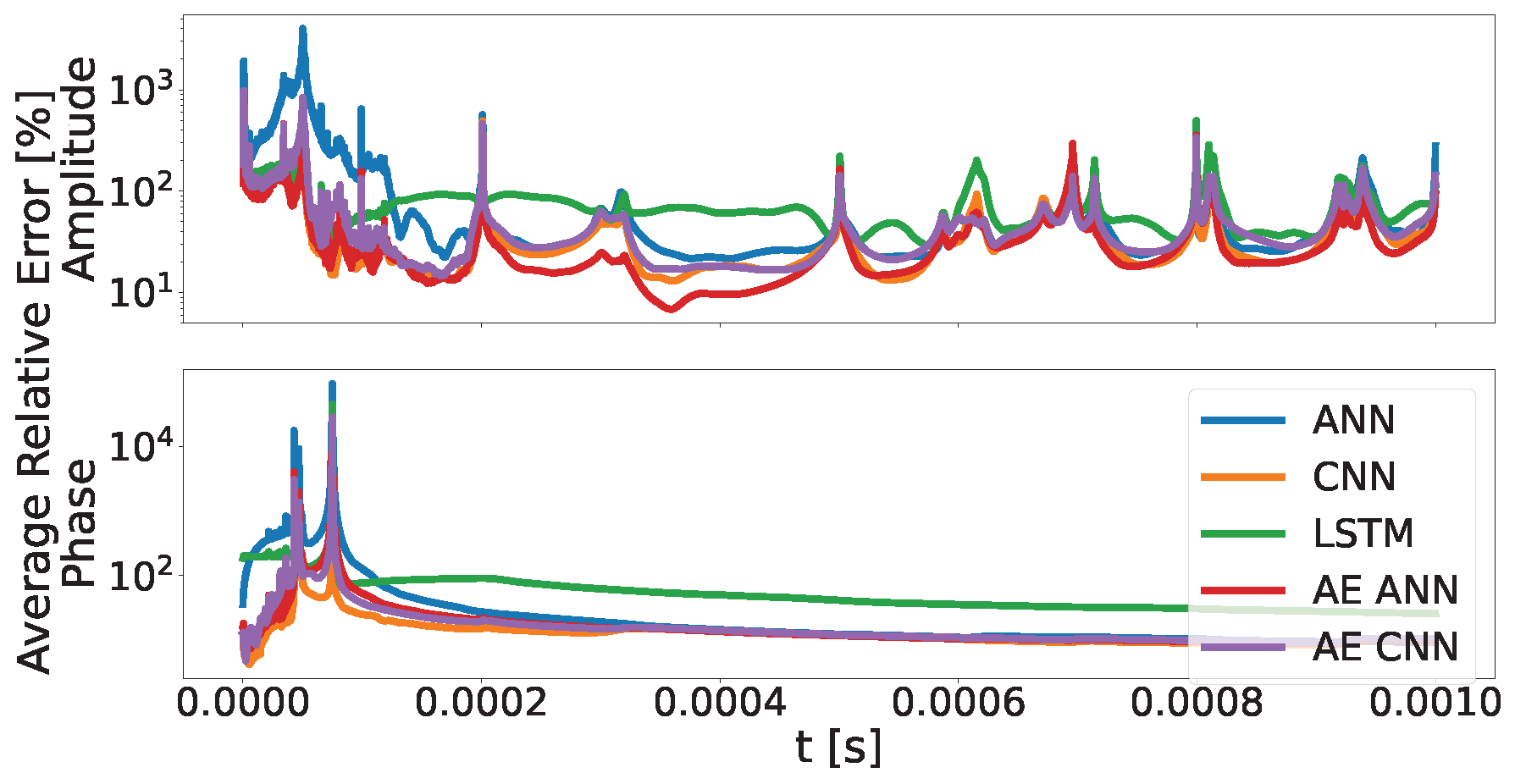
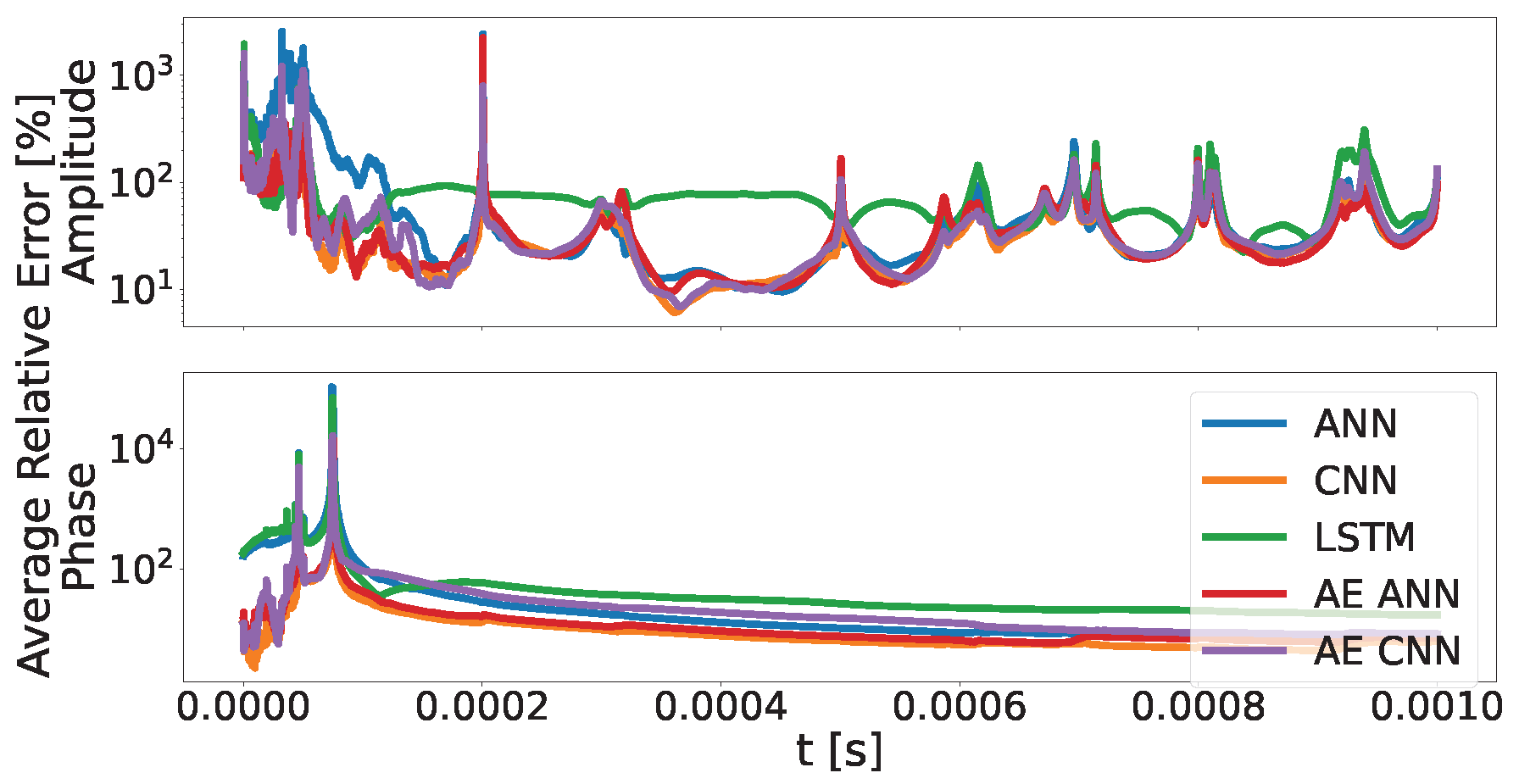
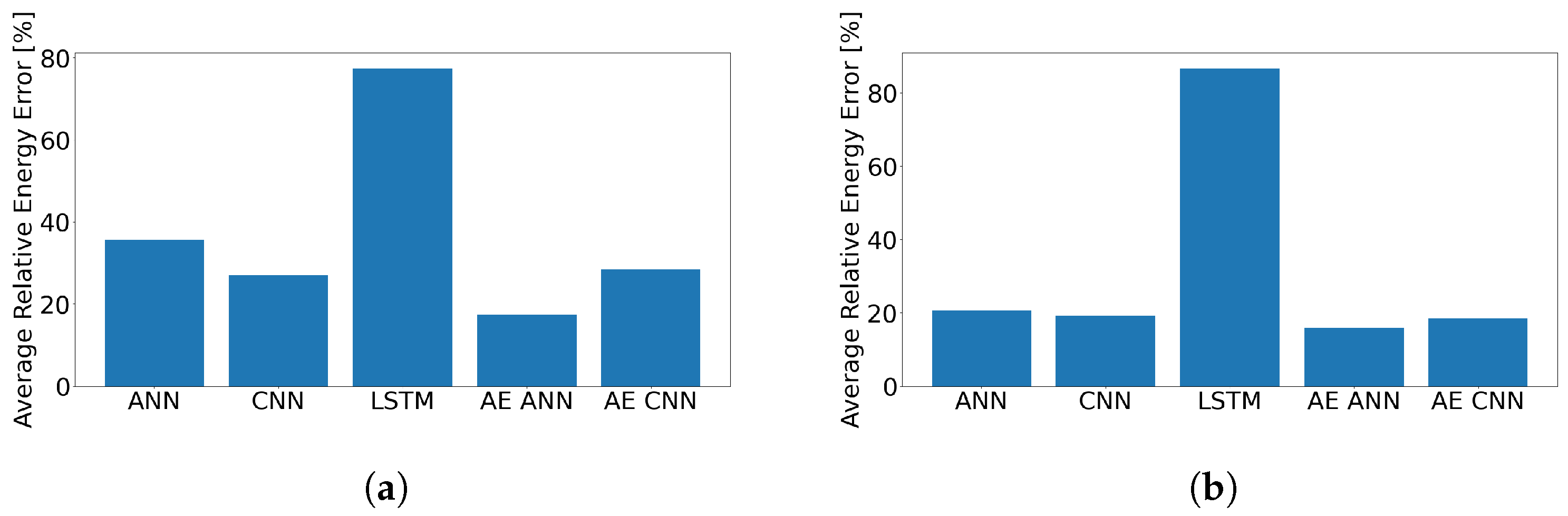
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GUW | Guided Ultrasonic Waves |
| SHM | Structural Health Monitoring |
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| AE | Auto Encoder |
| ACMS | Air-Coupled Measurement System |
| PWAS | Piezoelectric Wafer Active Sensor |
| MEMS | Micro-Electro-Mechanical System |
| PM | PWAS GUW Measurement |
| AM | Air-Coupled GUW Measurement |
| SSD | Single Signal Data |
| ASD | Average Signal Data |
| ARE | Averaged Relative Error |
| SE | Signal Energy |
References
- Farrar, C.; Worden, K. Structural Health Monitoring a Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Lamb, H. On Waves in an Elastic Plate. Proc. R. Soc. Lond. 1917, 93, 114–128. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Cawley, P.; Alleyne, D. The use of Lamb waves for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Structural Health Monitoring. Key Eng. Mater. 2004, 270, 14–21. [Google Scholar] [CrossRef]
- Lanza di Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am. 2008, 124, 161–174. [Google Scholar] [CrossRef] [PubMed]
- Schubert, K.J.; Brauner, C.; Herrmann, A.S. Non-damage-related influences on Lamb wave–based structural health monitoring of carbon fiber–reinforced plastic structures. Struct. Health Monit. 2014, 13, 158–176. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Tian, T.; Deng, D.; Hu, M.; Ma, J.; Gao, D.; Zhang, J.; Ma, S.; Yang, L.; et al. Guided ultrasonic wave, Machine learning, Structural health monitoring, Damage diagnostic, Impact diagnostic, Wave propagation. Ultrasonics 2023. [Google Scholar] [CrossRef] [PubMed]
- De Fenza, A.; Sorrentino, A.; Vitiello, P. Application of Artificial Neural Networks and Probability Ellipse methods for damage detection using Lamb waves. Compos. Struct. 2015, 133, 390–403. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Manson, G.; Worden, K. A numerically-enhanced machine learning approach to damage diagnosis using a Lamb wave sensing network. J. Sound Vib. 2014, 333, 4499–4525. [Google Scholar] [CrossRef]
- Rautela, M.; Gopalakrishnan, S. Ultrasonic guided wave based structural damage detection and localization using model assisted convolutional and recurrent neural networks. Expert Syst. Appl. 2021, 167, 114189. [Google Scholar] [CrossRef]
- Polle, C.; Bosse, S.; Herrmann, A.S. Damage Location Determination with Data Augmentation of Guided Ultrasonic Wave Features and Explainable Neural Network Approach for Integrated Sensor Systems. Computers 2024, 13, 32. [Google Scholar] [CrossRef]
- Wanhill, R.J.H. GLARE®: A Versatile Fibre Metal Laminate (FML) Concept. In Aerospace Materials and Material Technologies; Prasad, N.E., Wanhill, R.J.H., Eds.; Indian Institute of Metals Series; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Data Sheet SPU0410LR5H-QB. 2024. Available online: https://www.knowles.com/docs/default-source/model-downloads/spu0410lr5h-qb-revh32421a731dff6ddbb37cff0000940c19.pdf?Status=Master&sfvrsn=cebd77b1_4 (accessed on 14 October 2024).
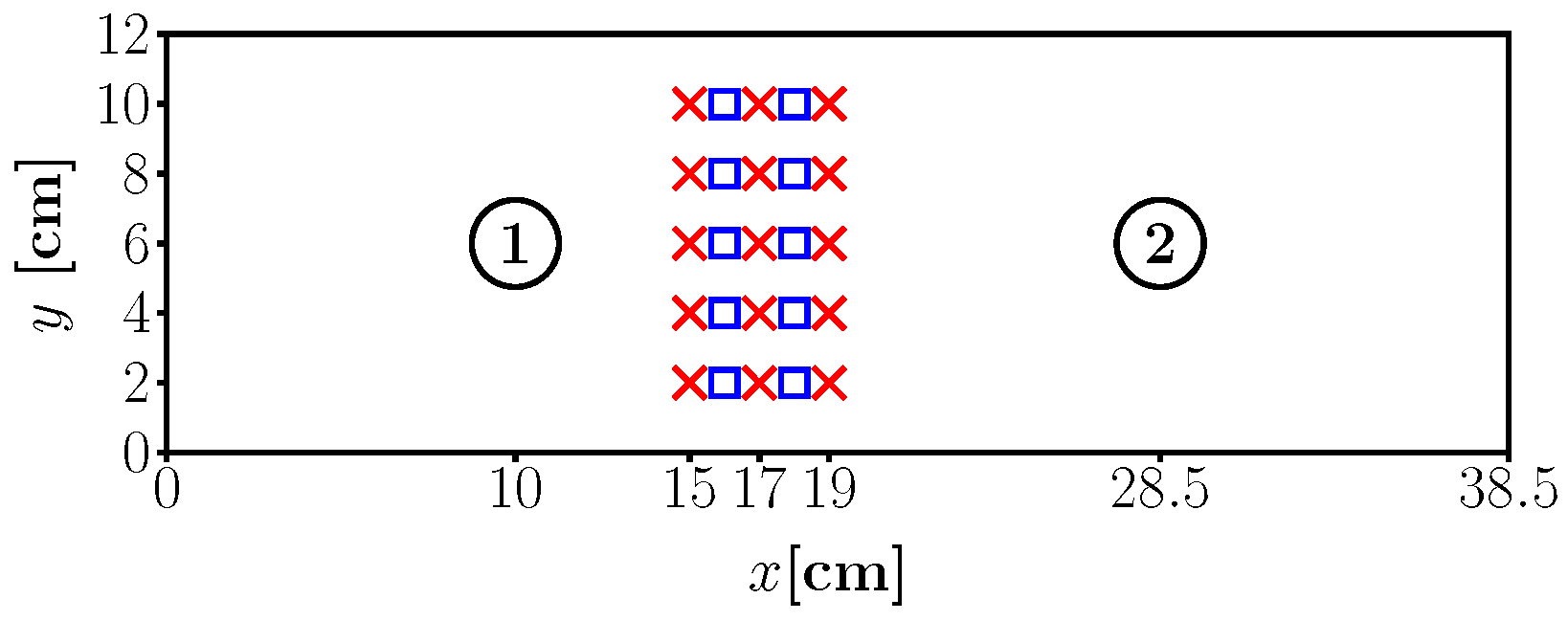



| Model | Layer Class | Parameters | Activation Function |
|---|---|---|---|
| ANN | Input | N: 6249; OS: [6249]; P: 0 | - |
| Dense | N: 6249; OS: [6249]; P: 39056250 | tanh | |
| Dense | N: 6249; OS: [6249]; P: 39056250 | linear | |
| CNN | Input | N: 6249; OS: [6249]; P: 0 | - |
| Conv1D | K: 16; KS: 12; S: 1; PC: valid; OS: [6227, 16]; P: 208 | tanh | |
| Conv1D | K: 16; KS: 12; S: 1; PC: valid; OS: [6227, 16]; P: 3088 | tanh | |
| Flatten | OS: [99632]; P: 0 | - | |
| Dense | N: 6249; OS: [6249]; P: 622606617 | tanh | |
| LSTM | Input | N: 6249; OS: [6249]; P: 0 | - |
| LSTM | N: 3; OS: [6249, 3]; P: 60 | tanh | |
| LSTM | N: 3; OS: [6249, 3]; P: 84 | tanh | |
| LSTM | N: 3; OS: [6249, 3]; P: 84 | tanh | |
| LSTM | N: 3; OS: [6249, 3]; P: 84 | tanh | |
| LSTM | N: 3; OS: [6249, 3]; P: 84 | tanh | |
| LSTM | N: 1; OS: [6249, 1]; P: 20 | tanh | |
| TimeDistributed(Dense) | N: 1; OS: [6249, 1]; P: 2 | linear | |
| ANN AE | Input | N: 6249; OS: [6249]; P: 0 | - |
| Dense | N: 124; OS: [124]; P: 775000 | tanh | |
| Dense | N: 64; OS: [64]; P: 7750 | tanh | |
| Dense | N: 124; OS: [124]; P: 7812 | tanh | |
| Dense | N: 6249; OS: [6249]; P: 781125 | linear | |
| CNN AE | Input | N: 6249; OS: [6249]; P: 0 | - |
| Conv1D | K: 64; KS: 4; S: 1; PC: same; OS: [6249, 64]; P: 320 | tanh | |
| AveragePooling1D | PS: 10; S: 5; PC: same; OS: [1250, 64]; P: 0 | - | |
| Conv1D | K: 64; KS: 4; S: 1; PC: same; OS: [1250, 64]; P: 16448 | tanh | |
| Flatten | OS: [80000]; P: 0 | - | |
| Dense | N: 1250; OS: [1250]; P: 100001250 | tanh | |
| Reshape | OS: [1250, 1]; P: 0 | - | |
| UpSampling1D | OS: [6250, 1]; P: 0 | - | |
| Cropping1D | OS: [6249, 1]; P: 0 | - | |
| Conv1DTranspose | K: 64; KS: 4; S: 1; PC: same; OS: [6249, 64]; P: 320 | tanh | |
| Dense | N: 6249; OS: [6249, 1]; P: 65 | linear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polle, C.; May, D.; Bosse, S. Transformation of Guided Ultrasonic Wave Signals from Air Coupled to Surface Bounded Measurement Systems with Machine Learning Algorithms for Training Data Augmentation. Eng. Proc. 2024, 82, 119. https://doi.org/10.3390/ecsa-11-20448
Polle C, May D, Bosse S. Transformation of Guided Ultrasonic Wave Signals from Air Coupled to Surface Bounded Measurement Systems with Machine Learning Algorithms for Training Data Augmentation. Engineering Proceedings. 2024; 82(1):119. https://doi.org/10.3390/ecsa-11-20448
Chicago/Turabian StylePolle, Christoph, David May, and Stefan Bosse. 2024. "Transformation of Guided Ultrasonic Wave Signals from Air Coupled to Surface Bounded Measurement Systems with Machine Learning Algorithms for Training Data Augmentation" Engineering Proceedings 82, no. 1: 119. https://doi.org/10.3390/ecsa-11-20448
APA StylePolle, C., May, D., & Bosse, S. (2024). Transformation of Guided Ultrasonic Wave Signals from Air Coupled to Surface Bounded Measurement Systems with Machine Learning Algorithms for Training Data Augmentation. Engineering Proceedings, 82(1), 119. https://doi.org/10.3390/ecsa-11-20448






