The Influence of Boundary Constraint Viscoelasticity on the Nonlinear Forced Vibration of Fluid-Conveying Layered Pipes †
Abstract
1. Introduction
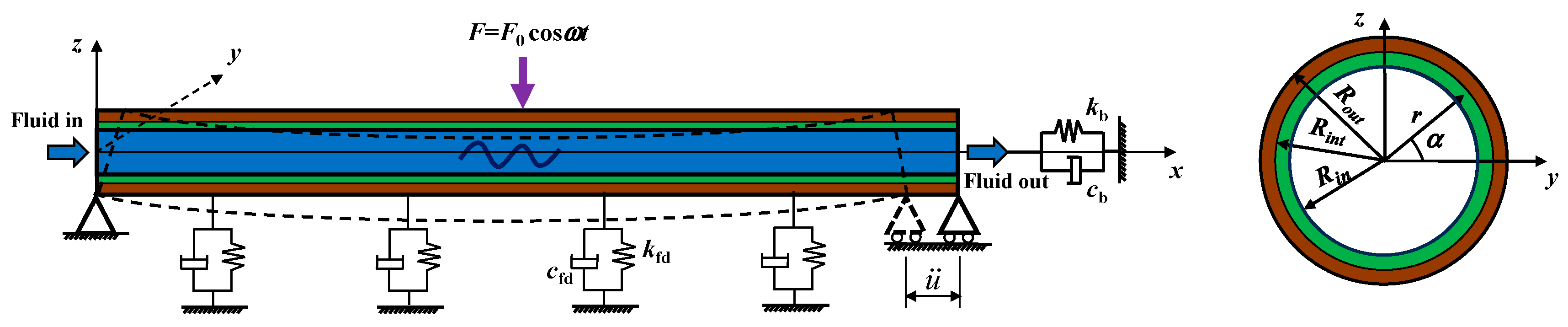
2. Theoretical Model and Solutions
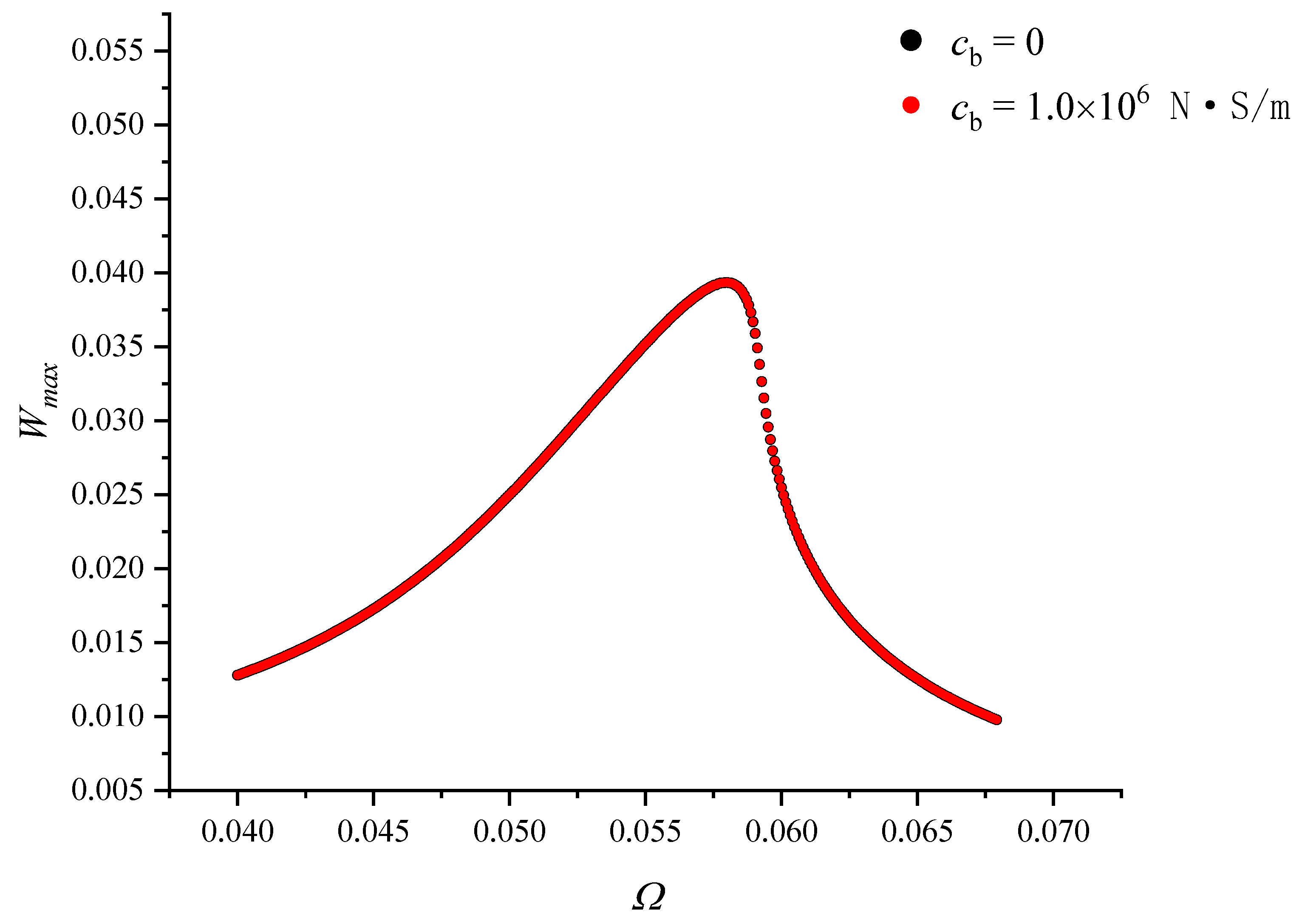
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.F.; Yao, M.H.; Zhang, W.; Wen, B. Dynamical Modeling and Multi-Pulse Chaotic Dynamics of Cantilevered Pipe Conveying Pulsating Fluid in Parametric Resonance. Aerosp. Sci. Technol. 2017, 68, 441–453. [Google Scholar] [CrossRef]
- Ma, W.L.; Jiang, Z.C.; Lee, K.Y.; Li, X.F. A refined beam theory for bending and vibration of functionally graded tube-beams. Compos. Struct. 2020, 236, 111878. [Google Scholar] [CrossRef]
- Khodabakhsh, R.; Saidi, A.R.; Bahaadini, R. An analytical solution for nonlinear vibration and post-buckling of functionally graded pipes conveying fluid considering the rotary inertia and shear deformation effects. Appl. Ocean. Res. 2020, 101, 102277. [Google Scholar] [CrossRef]
- Łuczko, J.; Czerwiński, A. Three-dimensional dynamics of curved pipes conveying fluid. J. Fluid. Struct. 2019, 91, 102704. [Google Scholar] [CrossRef]
- Wang, D.; Bai, C.; Zhang, H. Nonlinear vibrations of fluid-conveying FG cylindrical shells with piezoelectric actuator layer and subjected to external and piezoelectric parametric excitations. Compos. Struct. 2020, 248, 112437. [Google Scholar] [CrossRef]
- Dai, H.L.; Wang, L.; Qian, Q.; Ni, Q. Vortex-induced vibrations of pipes conveying pulsating fluid. Ocean Eng. 2014, 77, 12–22. [Google Scholar] [CrossRef]
- Ma, T.; Mu, A. Analysis of Nonlinear Vibration of Functionally Graded Simply Supported Fluid-Conveying Microtubes Subjected to Transverse Excitation Loads. Micromachines 2022, 13, 2114. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Li, L.; Jin, Q. Vibration and snap-through of fluid-conveying graphene reinforced composite pipes under low-velocity impact. AIAA J. 2021, 59, 5091–5105. [Google Scholar] [CrossRef]
- Zhou, K.; Ni, Q.; Dai, H.L.; Wang, L. Nonlinear forced vibrations of supported pipe conveying fluid subjected to an axial base excitation. J. Sound. Vib. 2020, 471, 115189. [Google Scholar] [CrossRef]
- Lacarbonara, W. Nonlinear Structural Mechanics: Theory, Dynamical Phenomena and Modeling; Springer Publishing Company: Rome, Italy, 2013. [Google Scholar]
- Wang, Z.; Ren, Y.; Meng, Q. Effect of boundary mobility on nonlinear pulsatile-flow induced dynamic instability of FG pipes. Struct. Eng. Mech. 2023, 86, 751–764. [Google Scholar]
- Fu, Y.; Zhang, P. Buckling and vibration of coreshell nanowires with weak interfaces. Mech. Res. Commun. 2010, 37, 622–626. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Meng, Q. The Influence of Boundary Constraint Viscoelasticity on the Nonlinear Forced Vibration of Fluid-Conveying Layered Pipes. Eng. Proc. 2024, 80, 19. https://doi.org/10.3390/engproc2024080019
Wang Z, Meng Q. The Influence of Boundary Constraint Viscoelasticity on the Nonlinear Forced Vibration of Fluid-Conveying Layered Pipes. Engineering Proceedings. 2024; 80(1):19. https://doi.org/10.3390/engproc2024080019
Chicago/Turabian StyleWang, Zhoumi, and Qingchun Meng. 2024. "The Influence of Boundary Constraint Viscoelasticity on the Nonlinear Forced Vibration of Fluid-Conveying Layered Pipes" Engineering Proceedings 80, no. 1: 19. https://doi.org/10.3390/engproc2024080019
APA StyleWang, Z., & Meng, Q. (2024). The Influence of Boundary Constraint Viscoelasticity on the Nonlinear Forced Vibration of Fluid-Conveying Layered Pipes. Engineering Proceedings, 80(1), 19. https://doi.org/10.3390/engproc2024080019




