Performance Optimization of a Formula Student Racing Car Using the IPG CarMaker, Part 1: Lap Time Convergence and Sensitivity Analysis ^†

Abstract

It is increasingly common for simulation and AI tools to aid in the vehicle design process. The IPG CarMaker uses a multibody vehicle model and a learning algorithm for the virtual driver. The goal is to discover the behavior of the learning algorithm from the point of view of reliability and convergence. Simulations demonstrate that the lap time converges reliably. We also report that small changes in the vehicle parameters induce small changes in the simulated lap time, i.e., the lap time is a differentiable function of the vehicle parameters. Part 2 of this paper explains the aerodynamics and Drag Reduction System optimization.

1. Introduction

Simulations, especially finite element analysis (FEA) [1], multibody dynamics (MBD) [2,3], and computational fluid dynamics (CFD) [1], are key elements that can help engineers be more effective in designing a brand-new commercial vehicle or a race car. The design process is usually an iterative process that aims at an optimal result [4], with multiple optimization goals, such as the lap time of a race car. The growing computational capacity is essential to save time during both the conceptual design and prototype testing once a proper simulation model is constructed. This work focuses on the lap time optimization of a formula student (FS) race car. A simulation model that is capable of reliable lap time prediction should generally contain all the fundamental components and properties of a car, including chassis stiffness, steering characteristics, suspension kinematics, a brake system, tire properties, inertias, and aerodynamic properties [5,6]. All these parameters are handled at a certain modeling level in the IPG CarMaker 11.0 software [7], which is mainly developed for predicting the dynamic behavior of four-wheeled vehicles. These computational tools have been used by the Arrabona Racing Team (ART), which was established in 2014 at the Széchenyi István University of Győr.

The IPG CarMaker software is used in the automotive and motorsport industries for the development of new vehicles. The simplified virtual representation of the vehicle can be defined in the software to analyze the behavior of it regarding the principles of vehicle dynamics. Further sub-systems, such as the virtual representation of the road and the virtual driver, are also parametrized in the IPG CarMaker software [7]. The software was used for designing the steering strategy of an FS car that uses four-wheel steering [8]. An enhanced Kalman filter scheme is developed in [9] to estimate the sideslip, the heading, and the longitudinal velocity of a vehicle, and the proposed design is tested by simulations using IPG CarMaker. A novel robust optimal controller is developed for active suspension systems to enhance a vehicle’s ride comfort and handling performance in [10]. The effectiveness of the controller is verified through simulation results using the IPG CarMaker software. Similarly, in [11], the IPG CarMaker vehicle dynamics software was used for the demonstration of the efficiency of a newly developed controller. The research works in references [9,10,11] shows that the IPG CarMaker is considered a reliable tool for scientific purposes.

The reliability of the vehicle model and the accuracy and precision of the simulation methodology were examined in this study. The first aim was to analyze the convergence properties of the lap time, which includes the optimization of the driver’s behavior in the IPG CarMaker. The second goal in this paper was to assess the sensitivity of the simulated lap time in relation to the vehicle parameters. The main results of the validation are also presented.

2. Methodology

2.1. Lap Time Simulations and Driver Model

A vehicle is generally simulated using MBD simulation tools when its dynamic behavior is in focus. A specific area in the motorsport world which also uses MBD is lap time simulation, which means that the theoretically possible fastest lap on the racetrack is predicted by assuming a perfect driver who does not make any errors and that the limitations of the vehicle are completely exploited, e.g., the traction budget is completely covered, or in other words, the lateral and longitudinal acceleration is maximized. This involves tire friction capabilities, engine capabilities, and the properties of the brake system. The key role of the aerodynamic package in the traction is considered as well. The aerodynamic map of the vehicle is presented in the second part [12] of this paper. Any change in the huge number of vehicle parameters yields a change in the simulated lap time. However, more importantly, the lap times in physical reality also change statistically. One can say “statistically”, because the actions of a real driver are always subjected to stochastic factors [13].

The simulations rely on a complex driver model built in the IPG CarMaker [7]. At the first adaptation stage, the driver model adapts to the vehicle: the vehicle limits, the engine speeds for shifting, and the controller dynamics are automatically determined. A set of different maneuvers are carried out in a huge, empty, plain ground using the current vehicle model. The trained driver model actuates the steering system, the gear shifting, the throttle, and the brake with an aim to be as fast as possible. In the second adaptation stage, the driver model learns the specific racetrack. Here, the learning rate (LR) is an important factor set by the user. It is identical to the LR used in neural networks. The driver adaptation is carried out during 15 laps along the track in our study. During that, the driver model parameters (invisible to the user) are being tuned to adapt to the specific racetrack. What the user sees is that the lap time is gradually decreasing. Each racetrack requires a unique driver adaptation procedure.

2.2. Vehicle Model

The vehicle model contains (a) the chassis of which the inertial parameters, the bending, and the torsional stiffness were experimentally measured; (b) the multilink suspension together with the steering mechanism and the anti-roll-bar, represented by a detailed geometry, as Figure 1 shows (the IPG CarMaker has its own tool to define the geometry and kinematics of the suspension system); (c) the tire model, which relies on the RealTime Tire model, in which the measured characteristics of the tire are stored in a Tire Data Exchange Format (TYDEX); (d) aero components represented by the aerodynamic map [12] originating from CFD simulations; (e) the engine, represented by the throttle–torque rotation speed map; and (f) the drivetrain, including all gears. The model validation helped to adjust the model parameters in such way that the simulated lap time is in the 1–2% vicinity of the actual lap time measured on the same track.

2.3. Lap Time Convergence, Parameter Sensitivity Analysis, and Validation

The analysis of the convergence of the lap time and the driver adaptation was carried out by initiating 15 consecutive laps on the track while registering the lap time data. The question is whether the lap time reaches a plateau after a certain number of laps. The lap time after 15 iterations is called the best lap time.

In the sensitivity analysis, the goal was to analyze the change in the best lap time in response to the change in the vehicle parameters. For this purpose, the mass of the chassis varied: starting from the actual value, it was increased and decreased with 3 15 kg steps. The best converged lap times were compared. The parameters which can influence the driver’s performance were set to an equal level in all cases, using 15 laps for the driver model to adapt to the racetrack.

The IPG CarMaker simulation results were validated by carrying out telemetry data collection during real test drives with the physical prototype on the test tracks [14]. Longitudinal and lateral acceleration data, together with throttle position data, were collected.

3. Results

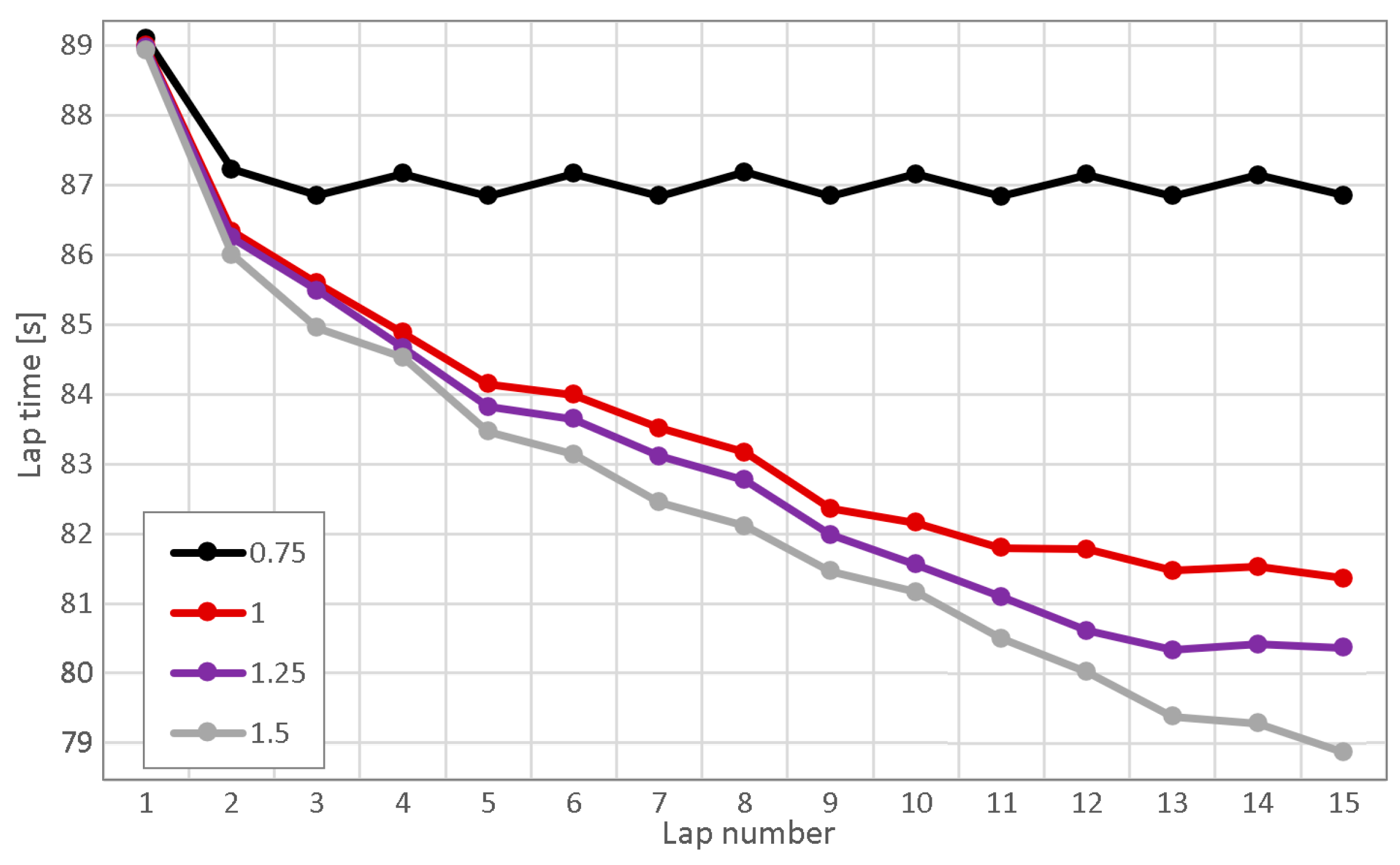
3.1. Convergence—Virtual Driver Adaptation Process

The LR was set to four different values to gain detailed information on the driver’s adaptation process: 0.75, 1, 1.25, and 1.5. Figure 2 shows the diagram of the lap times achieved by the virtual driver during the adaptation process, with different LR values. The obtained lap times are very close to the values measured in physical tests with experienced drivers. The mean value in the real test is about 79.5 s.

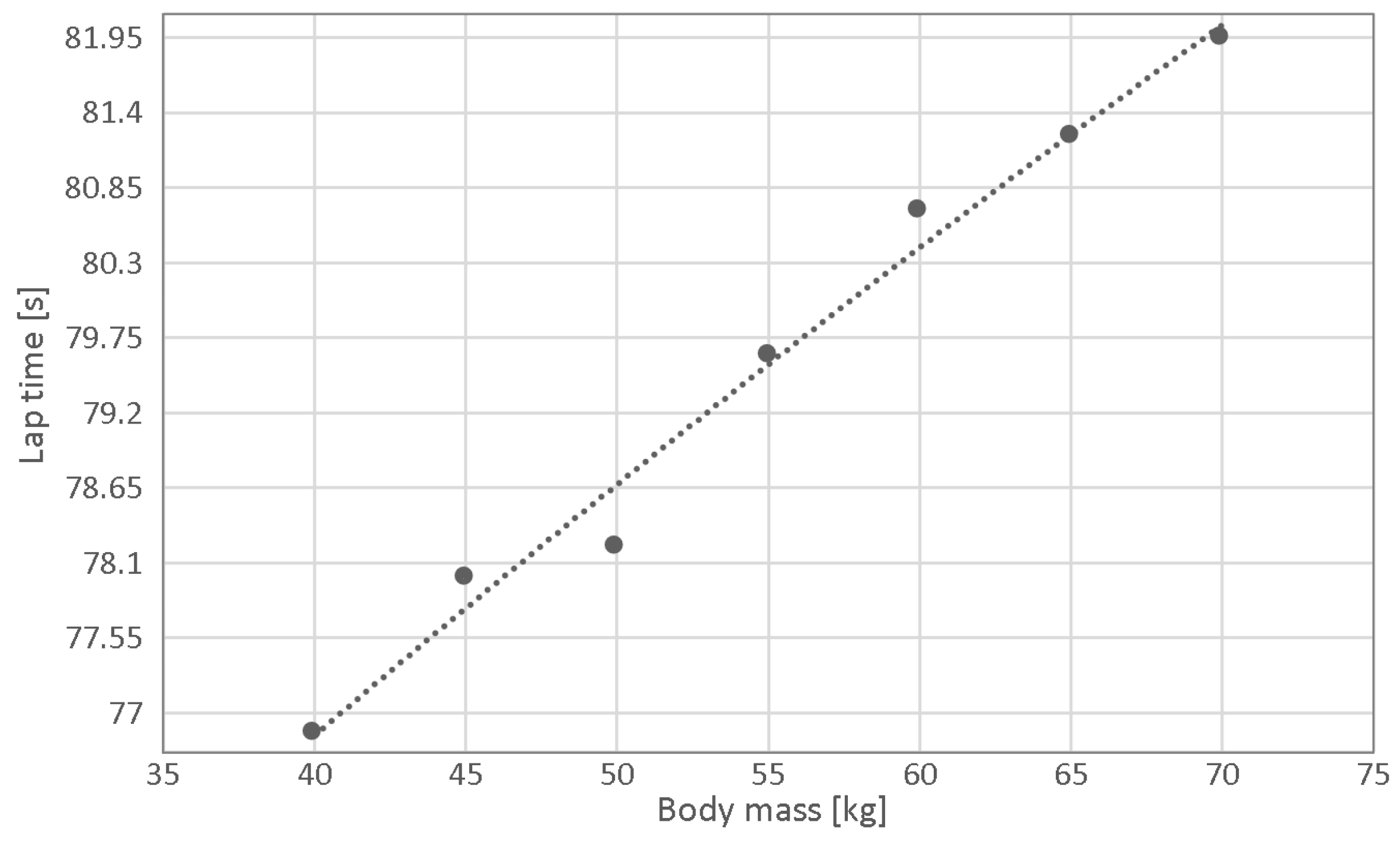
3.2. Parameter Sensitivity

The reference values for the body mass, total mass, and best lap time are 55 kg, 250 kg, and 79.62 s, respectively. The extreme values are, respectively, 40 kg, 235 kg, and 76.85 s and 70 kg, 265 kg, and 81.96 s. Figure 3 shows the lap times with the different body and auxiliary masses. A polynomial curve was fitted to the results to be able to examine the impact of this parameter on the results. The results show close-to-linear behavior, which is also expected in reality if the vehicle chassis mass increases or decreases.

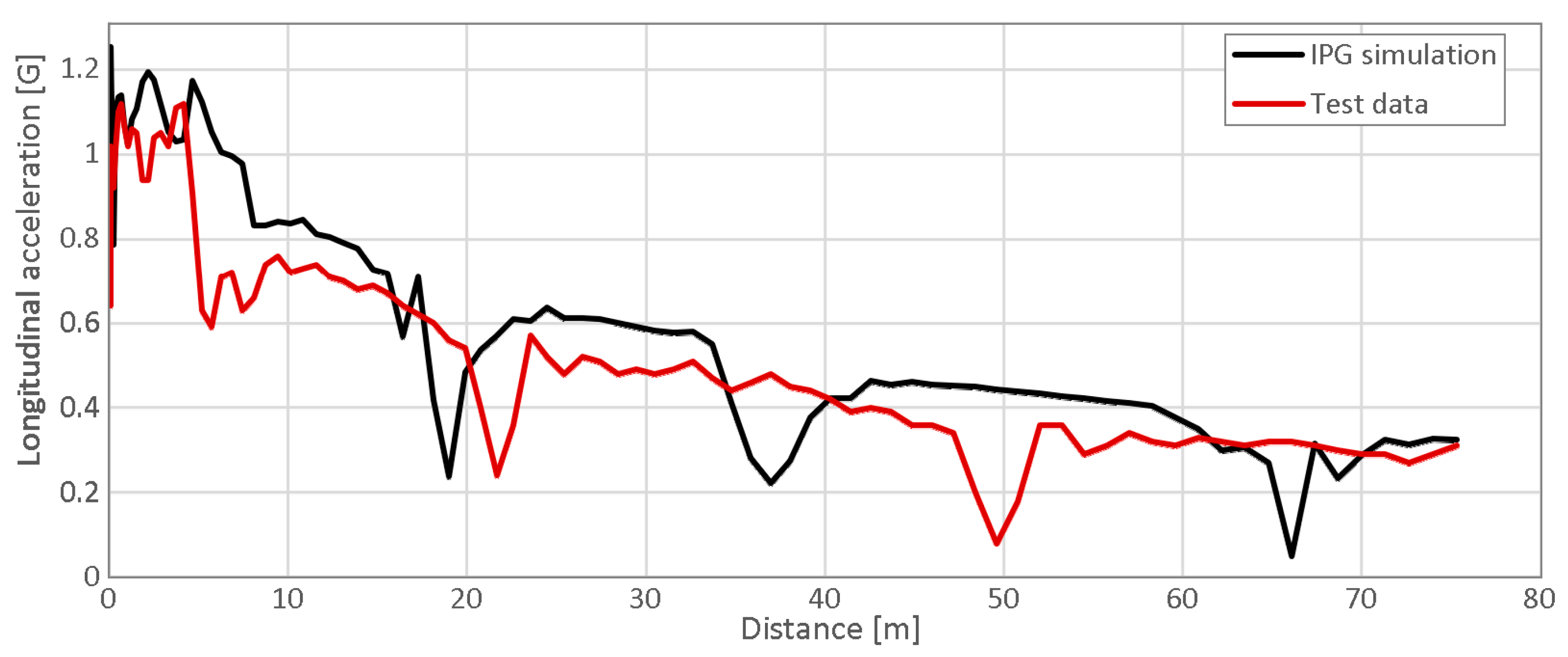
3.3. Validation of IPG CarMaker Simulations

During an FS competition, two sessions were used in this study: (i) standing-start acceleration on a 75 m straight track up to roughly 95 km/h, which is useful when validating the longitudinal behavior (see Figure 4); and (ii) a 250 m long skid pad test with a direction switch in the middle (a test track made of two connecting circles) [14], which is relevant for lateral vehicle properties (see Figure 5 and Figure 6). These two maneuvers are pre-defined in the IPG CarMaker. The setup of the vehicle is the same in the real-life test case and in the simulation. However, there are parameters that strongly affect vehicle performance but cannot be clearly defined, such as weather conditions, tire wear, and track conditions. For the minimization of these factors, test data were chosen from a day with average weather and track conditions with a fresh but not new set of tires. The physical data were collected with the data logger provided by MoteC. The simulated longitudinal acceleration in Figure 4 fits well to the measured data. However, at the present stage, we could not affect the gearshifts in the IPG car maker: it can be seen in the graphs that the real and the virtual drivers changed speeds at different time intervals. Figure 5 shows that the lateral accelerations of the simulations and the measurements match. However, the logged data are a bit noisy. Some minor difference is noticeable during the right-hand section, as the virtual model is reaching around a 1.6 G value, while the recorded real data averages about 1.4–1.5 G. This difference is due to the driver, as making a right-hand turn is a less natural maneuver for the drivers. In Figure 6, the throttle pedal position is displayed during a skid pad test. The IPG driver can keep a more consistent throttle pedal position, while the real driver is a bit more “nervous” with the throttle pedal, but the difference is not considerable.

4. Discussion and Conclusions

The newly designed combustion engine FS car prototype is developed in the IPG CarMaker virtual environment to be able to analyze its overall performance, such as the effect of the suspension geometry and stiffness, inertial parameters, and the aerodynamic settings, on the traction and the vehicle performance. The main dimensions and limits are controlled for the sake of fair competition and safety [14]. The physical tests and simulations make possible the near-optimal parameter choice from the range allowed by the rules.

A fundamental finding of this work was that the lap time converges reliably similarly to any iterative search algorithm. In reality, the driver’s behavior determines a huge portion of the overall performance [13]. Professional racing drivers therefore spend years in practice, going through many series until they are experienced enough to reach the physical limits of a certain vehicle on a certain track under different conditions. In IPG CarMaker, this process takes minutes. One can observe in Figure 2 that LR = 0.75 meant that the virtual driver was not able to find the track limits with this vehicle model. The convergence stops after three laps, and the lap times are far away from the best simulation and real-life results. LR values of 1 and 1.25 result in much better lap times and good convergence. Still, the lap times are 1.8 s and 0.7 s longer than the measured average. An LR = 1.5 results in faulty simulations, i.e., the vehicle drifts off the racetrack, which is handled as an error in the IPG CarMaker software. The conclusion is therefore that 1.25 is the optimal value for the LR on this track with this vehicle. An LR of 1.25 provides stable, reliable, repeatable, and realistic results. We emphasize that the learning process is always dependent on the vehicle with which it is performed and the tire model selected. As in real life, different vehicles and tires require different driving styles, and the driver must adapt to the car in some ways. If the virtual driver is placed in a more stable, easier-to-drive vehicle, the convergence characteristics is much steeper, and it easily finds the limits even with a lower LR value. In an unstable car, which requires careful driving, the lap times will decrease in smaller steps.

As a second finding, the lap time simulations in IPG CarMaker led to the conclusion that small changes in the vehicle mass induce small changes in the simulated lap time. Hence, the lap time is a continuous and differentiable function of the vehicle parameters. Part 2 of this paper [12] gives more information on the parameter sensitivity related to aerodynamic performance.

The reliability of the IPG CarMaker simulations were checked by means of validations. Measurements on the physical prototype were carried out. The acceleration data, the throttle actuation by the virtual driver, and the lap times were compared to the physical test results.