Comparative Evaluation of Forming Limit Curve Models for AlMg Alloys †
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
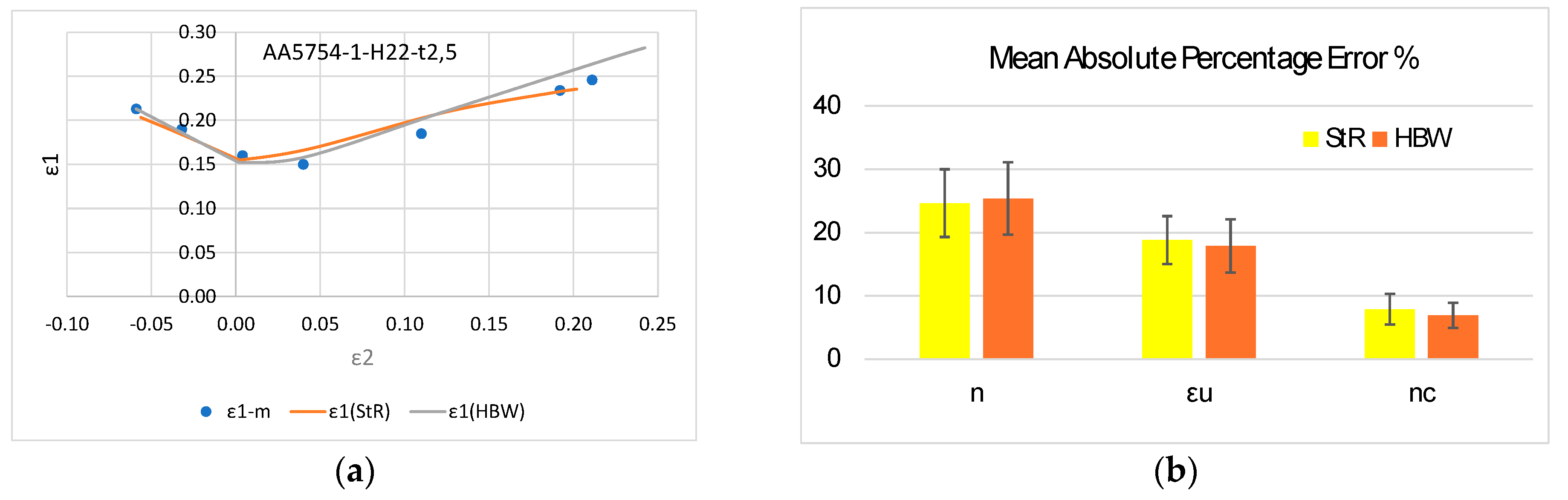
4.1. Analysis of the Stören–Rice and Hill–Bressan–Williams Models
4.2. Analysis of the MMFC Model
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marciniak, Z.; Duncan, J.L.; Hu, S.J. Mechanics of Sheet Metal Forming; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Banabic, D. Sheet Metal Forming Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Bressan, J.D.; Williams, J.A. The use of a shear instability criterion to predict local necking in sheet metal deformation. Int. J. Mech. Sci. 1983, 25, 155–168. [Google Scholar] [CrossRef]
- Stören, S.; Rice, J.R. Localized necking in thin sheets. J. Mech. Phys. Solids 1975, 23, 421–441. [Google Scholar] [CrossRef]
- Hora, P.; Tong, L.; Berisha, B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form. 2013, 6, 267–279. [Google Scholar] [CrossRef]
- Pham, Q.T.; Nguyen, D.T.; Kim, J.J.; Kim, Y.S. A graphical method to estimate forming limit curve of sheet metals. Key Eng. Mater. 2019, 794, 55–62. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, B.H.; Park, K.C.; Kim, J.S. Influence of the post-necking prediction of hardening law on the theoretical forming limit curve of aluminium sheets. Int. J. Mech. Sci. 2018, 140, 521–536. [Google Scholar] [CrossRef]
- Pham, Q.T.; Islam, M.S.; Sigvant, M.; Caro, L.P.; Lee, M.G.; Kim, J.S. Improvement of modified maximum force criterion for forming limit diagram prediction of sheet metal. Int. J. Solids Struct. 2023, 273, 112264. [Google Scholar] [CrossRef]
- Paul, S.K. Prediction of complete forming limit diagram from tensile properties of various steel sheets by a nonlinear regressionbased approach. J. Manuf. Process. 2016, 23, 192–200. [Google Scholar] [CrossRef]
- Abspoel, M.; Scholting, M.E.; Droog, J.M.M. A new method for predicting Forming Limit Curves from mechanical properties. J. Mater. Process. Technol. 2013, 213, 759–769. [Google Scholar] [CrossRef]
- Gerlach, J.; Kessler, L.; Köhler, A. The forming limit curve as a measure of formability—Is an increase of testing necessary for robustness simulations? In Proceedings of the International Deep Drawing Research Group (IDDRG) Conference, Graz, Austria, 31 May–2 June 2010; pp. 479–488. [Google Scholar]
- Paul, S.K. Theoretical analysis of strain- and stress-based forming limit diagrams. J. Strain Anal. Eng. Des. 2013, 48, 177–188. [Google Scholar] [CrossRef]
- Paul, S.K. Controlling factors of forming limit curve: A review. Adv. Ind. Manuf. Eng. 2021, 2, 100033. [Google Scholar] [CrossRef]
- Zhang, R.; Shao, Z.; Lin, J. A review on modelling techniques for formability prediction of sheet metal forming. Int. J. Light. Mater. Manuf. 2018, 1, 115–125. [Google Scholar] [CrossRef]
- Pham, Q.T.; Mac, T.B.; Kim, Y.S.; Nguyen, D.T. A comparative investigation on theoretical models for forming limit diagram prediction of automotive sheet metals. Mech. Based Des. Struct. Mach. 2021, 51, 1–15. [Google Scholar] [CrossRef]
- ISO 12004-2:2021; Metallic Materials—Determination of Forming-Limit Curves for Sheet and Strip Part 2: Determination of forming-limit Curves in the Laboratory. ISO: Geneva, Switzerland, 2021.
- ISO 6892-1:2019; Metallic Materials—Tensile Testing Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2019.

| Material | Rp0.2 (MPa) | Rm (MPa) | Ag (%) | Af (%) | n | r |
|---|---|---|---|---|---|---|
| AA5049-H22-t1,4 | 95 | 200 | 16.80 | 18.18 | 0.115 | 0.605 |
| AA5754--H22-t1,35 | 150 | 224 | 14.01 | 14.63 | 0.173 | 0.743 |
| AA5754-H22-t3 | 178 | 243 | 13.00 | 15.50 | 0.158 | 0.792 |
| AA5754-1-H22-t2,5 | 147 | 234 | 15.57 | 20.70 | 0.216 | 0.600 |
| AA5754-1-O-t2,5 | 80 | 217 | 21.06 | 25.26 | 0.380 | 0.678 |
| AA5754-2-H22-t2,5 | 141 | 236 | 18.90 | 22.90 | 0.212 | 0.569 |
| AA5754-2-O-t2,5 | 116 | 229 | 21.10 | 26.40 | 0.285 | 0.708 |
| AA5182-H22-t1,2 | 144 | 262 | 14.50 | 15.00 | 0.276 | 0.667 |
| AA5182-O-t3 | 132 | 260 | 20.50 | 22.00 | 0.264 | 0.713 |
| AA5182-H22-t3 | 230 | 318 | 11.30 | 13.30 | 0.157 | 0.734 |
| AA5182-O-t1,5 | 109 | 262 | 23.38 | 26.68 | 0.362 | 0.720 |
| AA5182-H-t1,5 | 129 | 269 | 21.73 | 24.49 | 0.310 | 0.761 |
| Material | ε*1 (0) | ε*1 (min) | ε*2 (min) | ε*1 (0.2) |
|---|---|---|---|---|
| AA5049-H22-t1,4 | 0.18 | 0.17 | 0.01 | 0.31 |
| AA5754--H22-t1,35 | 0.17 | 0.12 | 0.01 | 0.28 |
| AA5754-H22-t3 | 0.17 | 0.15 | 0.03 | 0.22 |
| AA5754-1-H22-t2,5 | 0.16 | 0.15 | 0.04 | 0.24 |
| AA5754-1-O-t2,5 | 0.22 | 0.21 | 0.03 | 0.27 |
| AA5754-2-H22-t2,5 | 0.19 | 0.16 | 0.02 | 0.24 |
| AA5754-2-O-t2,5 | 0.26 | 0.25 | 0.05 | 0.35 |
| AA5182-H22-t1,2 | 0.19 | 0.17 | 0.03 | 0.27 |
| AA5182-O-t3 | 0.25 | 0.24 | 0.05 | 0.32 |
| A5182-H22-t3 | 0.12 | 0.11 | 0.02 | 0.23 |
| AA5182-O-t1,5 | 0.28 | 0.26 | 0.06 | 0.28 |
| AA5182-H-t1,5 | 0.26 | 0.24 | 0.05 | 0.27 |
| Strain | S-M | V-M | S-H | V-H |
|---|---|---|---|---|
| ε1(0) − c | 37.16 | –30.36 | 38.10 | –27.76 |
| ε1(min) − c | 49.62 | –24.02 | 50.74 | –21.18 |
| ε1(0,2) − c | 49.08 | –27.29 | 54.90 | –16.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harangozó, D.; Czinege, I. Comparative Evaluation of Forming Limit Curve Models for AlMg Alloys. Eng. Proc. 2024, 79, 5. https://doi.org/10.3390/engproc2024079005
Harangozó D, Czinege I. Comparative Evaluation of Forming Limit Curve Models for AlMg Alloys. Engineering Proceedings. 2024; 79(1):5. https://doi.org/10.3390/engproc2024079005
Chicago/Turabian StyleHarangozó, Dóra, and Imre Czinege. 2024. "Comparative Evaluation of Forming Limit Curve Models for AlMg Alloys" Engineering Proceedings 79, no. 1: 5. https://doi.org/10.3390/engproc2024079005
APA StyleHarangozó, D., & Czinege, I. (2024). Comparative Evaluation of Forming Limit Curve Models for AlMg Alloys. Engineering Proceedings, 79(1), 5. https://doi.org/10.3390/engproc2024079005





