Performance Comparison of the General, the Dual, and the Joint Sigma Point Kalman Filters on State Estimation of Li-Ion Battery Cells for BMSs ^†

Abstract

Li-ion batteries, known for high energy and power density, are widely used in electromobility and stationary applications. In these applications a Battery Management System (BMS) ensures safety and longevity by performing functions like cell balancing and protecting against overcharge and over-discharge. Advanced BMSs estimate the battery’s State of Charge (SOC), crucial for determining remaining operating time and safe range. This study compares three Kalman Filter (KF)-based SOC estimation techniques: the general Sigma Point KF (SPKF), the joint SPKF, and the dual SPKF, for state and parameter estimation of a Samsung 18650INR13L Li-ion battery.

1. Introduction

Li-ion batteries, valued for their high energy and power density, are widely used in electromobility and stationary applications. Ensuring their safety and longevity requires a Battery Management System (BMS). Besides basic functions like cell balancing and protection, an advanced BMS must accurately estimate the battery’s State of Charge (SOC) to predict remaining operating time and maintain a safe range.

Traditional SOC estimation methods like Coulomb-counting are simple and fast but have limitations in handling noise and incremental bias. More effective are model-based estimators using an equivalent circuit model, such as the Randles circuit [1], like Kalman filters. Given the non-linear characteristics of Li-ion batteries, non-linear Kalman filters must be used, like the extended and unscented Kalman filters [2], providing accurate SOC predictions.

Battery parameters change over time due to temperature and aging, affecting estimation accuracy. The joint and dual Sigma Point Kalman Filters (SPKFs) address this by estimating states and parameters, with joint SPKF augmenting the state matrix with parameters and dual SPKF using separate filters for state and parameter estimation [3,4]. This study compares the performance of the general, joint, and dual SPKF in estimating the states and parameters of a Li-ion battery cell.

2. Dynamic Model of the Battery

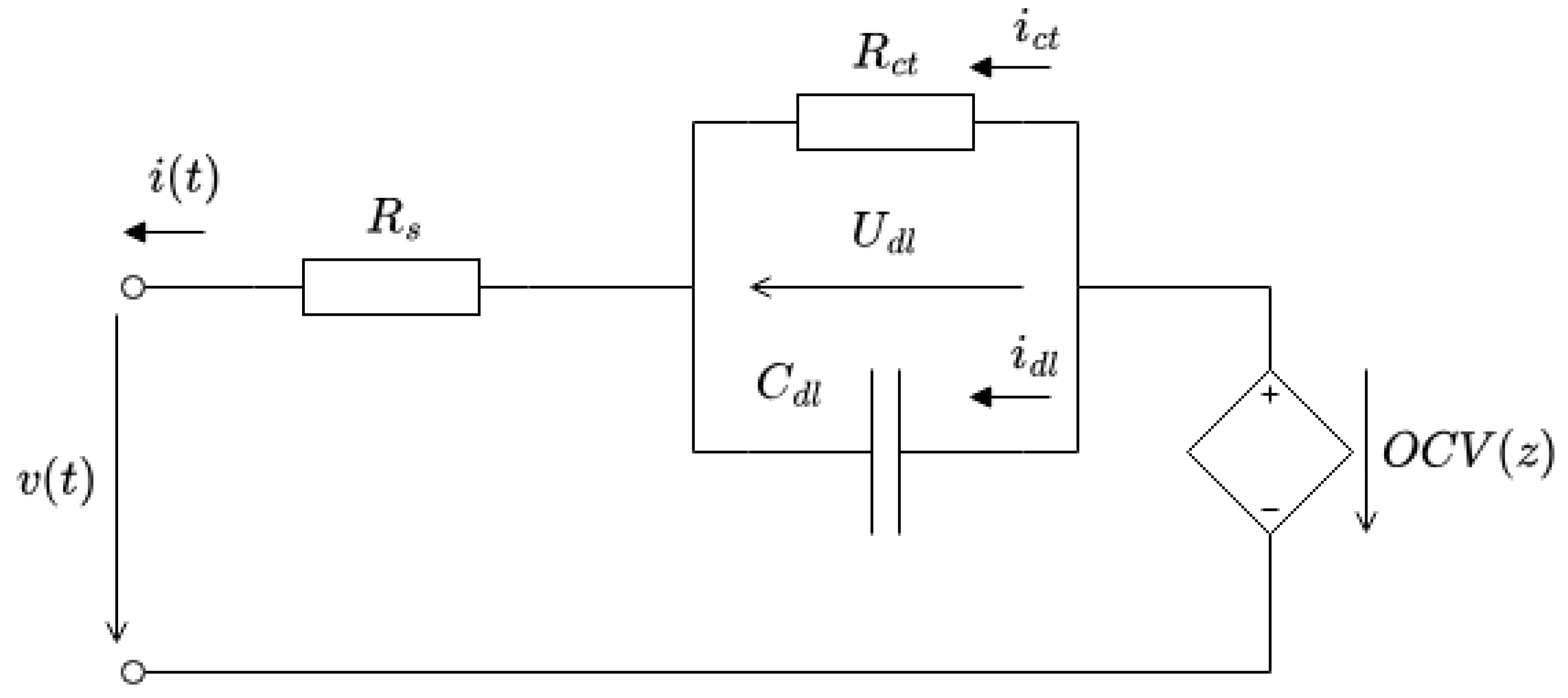
To model the battery characteristics, the Randles equivalent circuit has been applied as described in [5], which is depicted in Figure 1, and the discretized state-space model of the equivalent circuit is:

$$\left[\begin{array}{c}{z}_{k+1}\\ i_{ct,k+1}\end{array}\right]=\left[\begin{array}{c}{z}_k-\eta {\displaystyle \frac{\mathsf{\Delta }t}{Q}}{i}_k\\ e^{-{\displaystyle \frac{\mathsf{\Delta }t}{\tau }}}{i}_{ct,k}+\left(1-e^{{\displaystyle \frac{\mathsf{\Delta }t}{\tau }}}\right)i_k\end{array}\right]$$

(1)

$$y_k=OCV\left(z_k\right)-R_{ct,k}{i}_{ct,k}-R_{s,k}{i}_k,$$

(2)

where ${\mathit{R}}_{\mathit{c}\mathit{t}}$ denotes the charge-transfer resistance, ${\mathit{R}}_{\mathit{s}}$ is the serial resistance of the cell, ${\mathit{C}}_{\mathit{d}\mathit{l}}$ represents the double-layer capacity, ${\mathit{z}}_{\mathit{k}}$ is the cell’s state of charge, $\mathsf{\tau }={\mathit{R}}_{\mathit{c}\mathit{t}}{\mathit{C}}_{\mathit{d}\mathit{l}}$ is the time constant of the ${\mathit{R}}_{\mathit{c}\mathit{t}}$-${\mathit{C}}_{\mathit{d}\mathit{l}}$ subsystem, and $\mathsf{\Delta }\mathit{t}$ is the sampling time. $\mathsf{\eta }$ is the Coulombic efficiency and $\mathit{Q}$ is the capacity of the cell. The $\mathit{O}\mathit{C}\mathit{V}\left(\mathit{z}\right)$ is the Open Circuit Voltage (OCV), which is the function of the SOC. $\mathit{i}\left(\mathit{t}\right)$ is the cell current, which is the sum of ${\mathit{i}}_{\mathit{c}\mathit{t}}$ and ${\mathit{i}}_{\mathit{d}\mathit{l}}$, and $\mathit{v}\left(\mathit{t}\right)$ is the cell’s terminal voltage.

3. The Sigma Point Kalman Filter

The Kalman filter is the optimum state estimator for linear systems with uncorrelated zero-mean Gaussian process and measurement noise. In the case of battery cells, because of the $OCV\left(z\right)$ function the system is nonlinear, so the use of a nonlinear Kalman filter is needed. Nonlinear Kalman filters are based on the nonlinear state-space model of the system:

$${\dot{x}}_{k+1}=f_k\left(x_k,u_k\right)+w_k,$$

(3)

$${\mathrm{y}}_{\mathrm{k}}={\mathrm{h}}_{\mathrm{k}}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)+{\mathrm{v}}_{\mathrm{k}},$$

(4)

where $x$ is the state vector, $u$ is the input vector, $y$ is the output vector, and $k$ is the unit delay. $w$ is the Gaussian process noise with 0 mean and $Q$ covariance and $v$ is the Gaussian measurement noise with 0 mean and $R$ covariance.

The fundamental concept of sigma point Kalman filter methods is that the system’s state and output equations are evaluated at a specific number and value of so-called sigma points. The mean and covariance of the resulting state and output sigma point vectors provide the predicted states, outputs, and the covariance of their errors.

The evaluation of a function $f\left(\right)$ with a random vector input using sigma points is performed as follows [6]:

• Select sigma points $\mathcal{X}$ such that their weighted mean and covariance match those of the input random variable;
• Evaluate the function $f\left(\right)$ at each sigma point, obtaining the output sigma points $\mathcal{Y}$;
• Finally, compute the mean $\overline{y}$ and covariance $P_y$ of the function’s output from the output sigma points $\mathcal{Y}$.

To determine the sigma points, we need the mean $\overline{x}$ and covariance $P_x$ of the random vector $x$ to be modeled. If the random vector has $n$ elements, the $2n+1$ sigma points used for modeling can be determined as follows:

$$\mathcal{X}=\left\{\overline{x},\overline{x}+\mathsf{\gamma }\sqrt{P_x},\overline{x}-\mathsf{\gamma }\sqrt{P_x}\right\},$$

(5)

where $\sqrt{P_x}$ is a lower triangular matrix computed using Cholesky decomposition. The mean of the input random vector from the sigma points is calculated as:

$$\overline{x}=\sum _{i=0}^{2n}{\mathsf{\alpha }}_i^{\left(m\right)}{\mathcal{X}}_{\mathcal{i}},$$

(6)

and the covariance is:

$$P_x=\sum _{i=0}^{2n}{\mathsf{\alpha }}_i^{\left(c\right)}\left({\mathcal{X}}_{\mathcal{i}}-\overline{x}\right){\left({\mathcal{X}}_{\mathcal{i}}-\overline{x}\right)}^T,$$

(7)

where ${\mathcal{X}}_i$ is the $i$-th sigma point in $\mathcal{X}$, and $\mathsf{\gamma }$, ${\mathsf{\alpha }}_i^{\left(m\right)}$, and ${\mathsf{\alpha }}_i^{\left(c\right)}$ are weighting factors influencing the calculation of the sigma points, the mean of the modelled variable, and the covariance. After evaluating the function at the input sigma points, the mean and covariance of the output random vector can be calculated similarly to the input random vector.

The various SPKF methods differ only in the determination of the weighting factors. In the case of the Unscented KF (UKF) we have three tuning parameters, and in the case of the Central Difference KF (CDKF) we only have $h$. The exact method for calculating the weighting factors from the tuning parameters can be found in [6].

Using the sigma point method, the general steps of the SPKF can be derived:

• For predicting the next state:
  • First, create an augmented state matrix ${\widehat{x}}_{k-1}^{a,+}$ using the previous estimated state, process noise, and measurement noise, and an augmented block diagonal covariance matrix $P_{\tilde{x},k-1}^{a,+}$ using the previous estimation error covariance, process noise covariance, and measurement noise covariance;
  • Using these and Equation (5) the sigma points are generated;
  • Where for $n$ state variables, the first $n$ rows contain the sigma points ${\mathcal{X}}_{k-1}^{x,+}$ for state variables, the next $n$ rows contain sigma points ${\mathcal{X}}_{k-1}^{w,+}$ for process noise, and the subsequent rows contain sigma points ${\mathcal{X}}_{k-1}^{v,+}$ for measurement noise;
  • To determine the next state prediction, evaluate the state Equation (3) using the sigma points for state variables and process noise. From the resulting sigma points, the next predicted state can be determined using Equation (6).
• The covariance of the state prediction error $P_{k+1}^{-}$ can be determined using the sigma points for state variables and Equation (7);
• To determine the system output, evaluate the output Equation (4) using the sigma points for state variables and measurement noise, and the output estimate ${\widehat{y}}_k$ is computed using Equation (6);
• To determine the Kalman gain, first calculate the covariance matrix $P_{\tilde{y},k}$ for the output estimate using Equation (7).as well as the cross-covariance between the state prediction and the output estimate:

  $${\mathrm{P}}_{\tilde{\mathrm{x}}\tilde{y},k}=\sum _{\mathrm{i}=0}^{2\mathrm{n}}{\mathsf{\alpha }}_{\mathrm{i}}^{\left(\mathrm{c}\right)}\left({\mathcal{X}}_{\mathcal{k},\mathcal{i}}^{\mathcal{x},-}-{\widehat{x}}_k^{-}\right){\left({\mathcal{Y}}_{\mathcal{k},\mathcal{i}}-{\widehat{y}}_k\right)}^{\mathrm{T}}.$$

  (8)
  Using these covariance matrices, the Kalman gain is:

  $${\mathrm{K}}_{\mathrm{k}}=P_{\tilde{x}\tilde{y},k}{\mathrm{P}}_{\tilde{\mathrm{y}},\mathrm{k}}^{-1}.$$

  (9)
• The correction step is performed in the same manner as in all Kalman filters:

  $${\widehat{x}}_k^{+}={\widehat{x}}_k^{-}+{\mathrm{K}}_{\mathrm{k}}\left({\mathrm{y}}_{\mathrm{k}}-{\widehat{y}}_k\right)$$

  (10)
• Finally, the estimation error covariance is updated as:

  $$P_{\tilde{x},k}^{+}=P_{\tilde{x},k}^{-}-K_k{P}_{\tilde{y},k}{K}_k^T.$$

  (11)
• To implement the sigma point Kalman filter for state observation of the cell model, the previously described SPKF method should be applied using the system Equation (1) and the output Equation (2) of the cell model. In this article, a CDKF sigma point Kalman filter is implemented.

4. The Joint Sigma Point Kalman Filter

The joint form of the sigma point Kalman filter is based on the classical mathematical formulae that are used for state estimation. In order to estimate the parameters as well as the states at the same time, the state vector is expanded by the ${\mathsf{\Theta }}_k$ parameter vector to form an augmented state vector. The estimated parameters of the model are ${\mathsf{\Theta }}_k^1=R_{ct}$, ${\mathsf{\Theta }}_k^2=Q$, and ${\mathsf{\Theta }}_k^3=R_s$. By estimating the $R_{ct}$ parameter the time constant of the $R_{ct}$-$C_{dl}$ subsystem changes, so the estimation of $C_{dl}$ is not needed. Instead, the cell capacity and by it the State of Health (SOH) of the cell is estimated:

$$SOH={\displaystyle \frac{Q_k}{Q_0}}100\%$$

(12)

The fundamental form of joint estimation is:

$$\left[\begin{array}{c}{x}_{k+1}\\ {\mathsf{\Theta }}_{k+1}\end{array}\right]=\left[\begin{array}{c}{f}_k\left(x_k,u_k,{\mathsf{\Theta }}_k\right)\\ {\mathsf{\Theta }}_k\end{array}\right]+\left[\begin{array}{c}{w}_k\\ r_k\end{array}\right]$$

(13)

$$\left[\begin{array}{c}{y}_k\\ {\Theta }_k\end{array}\right]=\left[\begin{array}{c}{h}_k\left(x_k,u_k,{\Theta }_k\right)\\ {\Theta }_k\end{array}\right]+v_k,$$

(14)

where $r_k$ is a zero-mean, Gaussian noise to drive the change in parameters, and the estimated parameters are also included in the measurement equation so the $R_k$ matrix can contain covariance values for them too.

The joint SPKF can be implemented by applying the general SPKF method for the augmented state vector, state equation, and noise matrix. In Equation (10) when calculating the error between the measured and the predicted output for the included parameters the estimated value is subtracted from the previous estimation.

5. The Dual Sigma Point Kalman Filter

In the case of dual estimation, two Kalman filters are implemented with mixed signals, one for estimation of states and another for parameters. The goal is the same as in the case of the joint estimation, but because of the smaller matrix sizes the computational complexity is lower. However, by having separate matrices for state and parameter estimation the cross-covariance between the two is lost, leading to possibly poorer performance.

The state equation for the state estimator uses the parameter vector as an input and can be written as:

$$x_{k+1}=f_k\left(x_k,u_k,{\mathsf{\Theta }}_k\right)+w_k.$$

(15)

The model for the parameter estimator is:

$${\mathsf{\Theta }}_{k+1}={\mathsf{\Theta }}_k+r_k,$$

(16)

where $r_k\sim \left(0,P_{r_k}\right)$ is 0 mean, Gaussian, and has $P_{r_k}$ covariance matrix.

To implement the dual SPKF, the general SPKF steps are implemented for the state estimator and for the parameter estimator as well and the two estimators use the estimated values of each other. The measurement equation of the parameter estimator and the state estimator is the same, but because of the different number of sigma points it needs to be evaluated separately.

6. Model Identification

The performance of three Kalman filter methods was evaluated for state and parameter estimation of a Samsung INR18650-13L battery cell under various operating conditions. The data used in this analysis were provided by our colleagues at the University, and the complete dataset along with detailed measurement information is available in [7].

To model the battery cell, the capacity, Coulombic efficiency, and $OCV\left(z\right)$ curve were determined from constant charge and discharge measurements conducted at $0.1$C between the maximum voltage and $3$ V at 25 °C. The cell’s capacity, calculated as the total charge removed during constant discharge, was found to be $1251$ mAh. The Coulombic efficiency, derived from the ratio of total charge absorbed during charging to total charge removed during discharging, was $0.9077$. 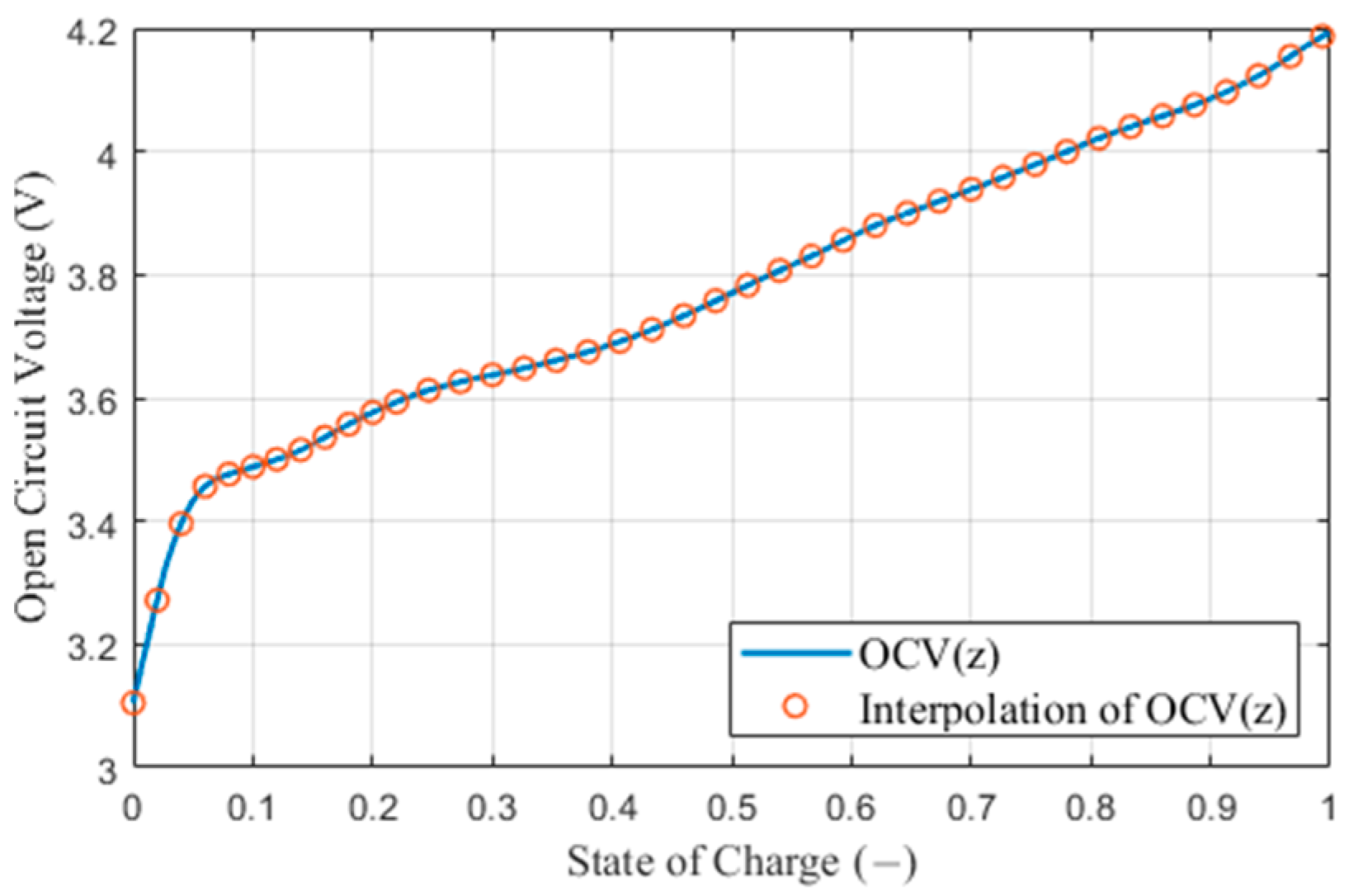The $OCV\left(z\right)$ curve is the weighted average of the terminal voltage during constant charge and discharge operations, where the weighting factor is the current. For the model, the $OCV\left(z\right)$ function was interpolated using piecewise linear interpolation. The resulting $OCV\left(z\right)$ curve is shown in Figure 2.

The series resistance, charge transfer resistance, and double-layer capacitance parameters of the model were identified from the transient discharge measurement of the cell at 25 °C. During the measurement, 1C discharge current was applied on the cell for 360 s periodically with 60 s of relaxation. The parameters were estimated based on exponential regression where the “lsqcurvefit” function in Matlab was used for fitting. The calculated parameters were used for the general SPKF and as an initial value for the joint and dual SPKFs. The identified parameter values are $C_{dl}=647.2F$, $R_{ct}=0.0402\mathsf{\Omega }$, and $R_s=0.08\mathsf{\Omega }$.

7. Comparison of the SPKF Methods

The performance of the three SPKF implementations was evaluated by estimating the state and parameters of the battery cell during a Worldwide Harmonized Light-Duty Vehicles Test Procedure (WLTP), followed by a 1C discharge of the cell at different temperatures. In the paper, we only present the results at 25 °C, but temperature differences do not significantly affect performance due to the parameter estimation.

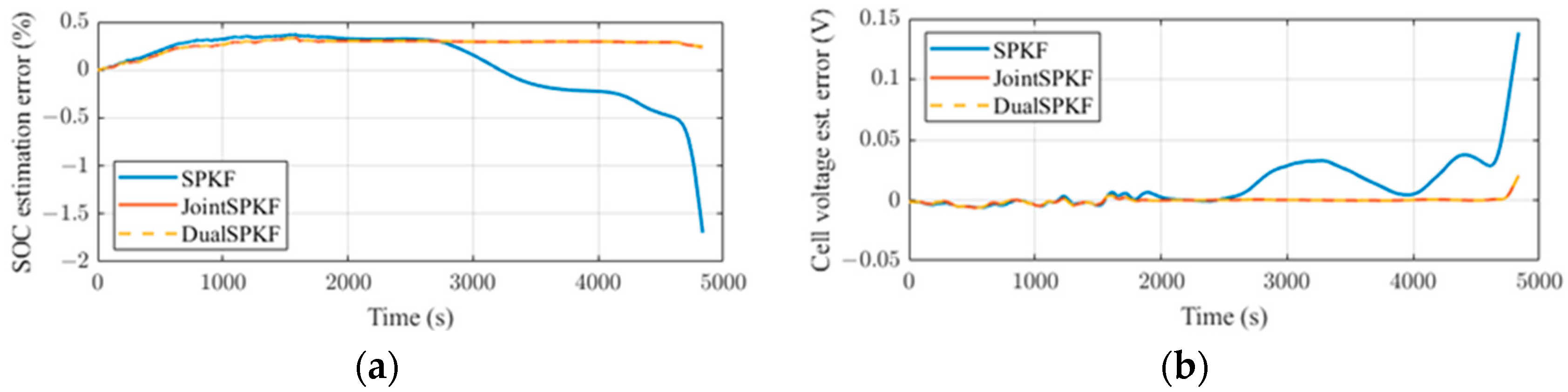
The SOC and cell voltage estimation error by the three SPKFs is shown in Figure 3. Initially, the accuracy of all three SPKF methods is comparable, as the initial parameters are close to the actual values. However, as the model parameters begin to deviate from their true values, the performance of the general SPKF declines. Conversely, the dual and joint SPKF methods manage to correct the errors by estimating the parameter values.

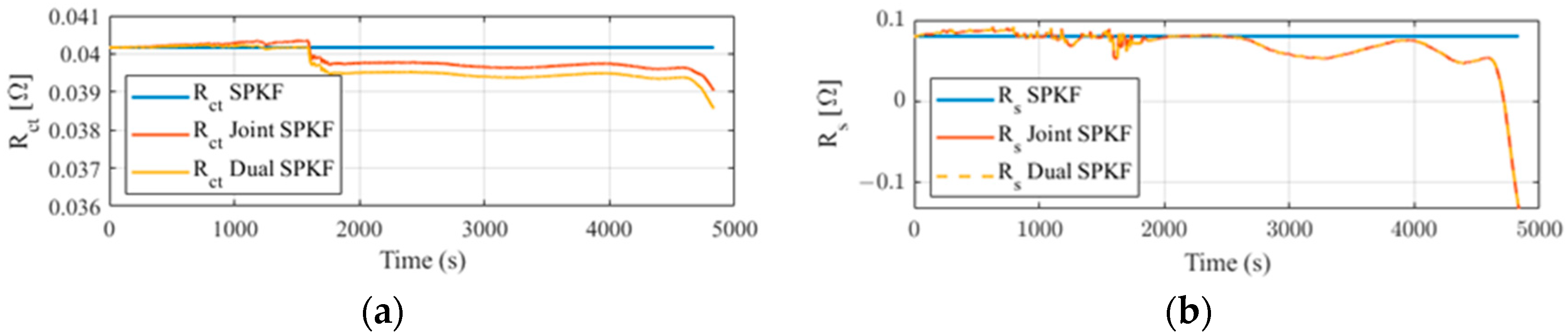
Figure 4 shows the estimated $R_{ct}$ and $R_s$ parameters of the cell. Since the cell capacity remains approximately constant during the test, it is not included in the figure. It can be observed that the error in the identified $OCV\left(z\right)$ function is primarily compensated by the series resistance parameter. By adjusting the $Q_k$, $R_k$, and $P_{r_k}$ covariance matrices of the Kalman filters, the extent of this parameter adjustment can be controlled, allowing to determine how much the filters should compensate for errors in the $OCV\left(z\right)$ curve.

The three filters were implemented in a Matlab/Simulink environment. Simulating the $4834.5$ s long measurement took $0.914$ s in the case of the general SPKF of which calling the block for the SPKF took 0.303 s. In the case of the joint SPKF, the simulation lasted for $1.649$ s of which the joint SPKF block took 0.953 s. Simulating the measurement with the dual SPKF took $1.488$ s of which the filter ran for $0.893$ s. Both the joint and dual SPKFs had a significantly higher computational cost than the general SPKF, but running the dual SPKF took $0.06$ s less than running the joint SPKF which is an about $6.3$% better performance in computational cost.

This difference is caused by the smaller matrix operations, but because the sigma point method in itself requires large matrix operations, separating the state and parameter variables does not cause that significant change.

8. Conclusions

In this paper the general, the joint, and the dual sigma point Kalman filters were implemented for estimating the state and parameters of a Samsung 18650INR13L Li-ion battery cell. Their performance was compared on state estimation and computational cost on a WLTP test cycle followed by a 1C discharge of the cell. It was shown that the dual and joint SPKFs outperformed the general SPKF with the help of estimating the cell parameters along with the states, leading them to be able to compensate for the parameter drift occurring during the operation of the cell. These two methods could estimate the battery states similarly, but the dual SPKF had an approximately 6% better computational performance which is not that significant but can be beneficial in the case of implementation in a BMS. To improve the robustness of these Kalman filters, the estimation of the cell capacity was also implemented, making them able to maintain their performance despite the cell aging.