Numerical Approach to Fatigue Life Prediction of Harrow Tines Considering Geometrical Variations †
Abstract
1. Introduction
2. Materials and Design
3. Numerical Analysis and Rapid Prototyping
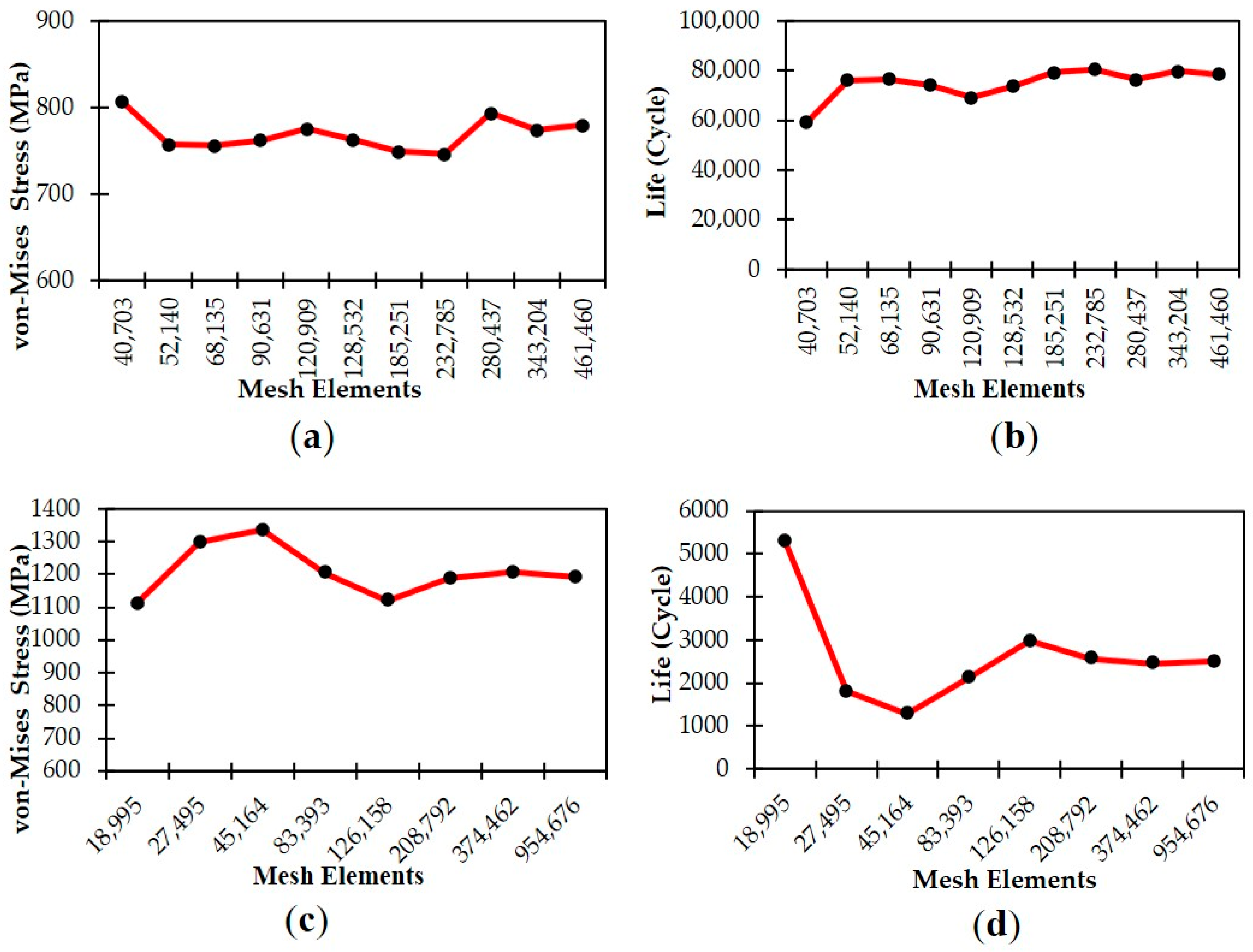
3.1. Mesh Convergence
3.2. Fatigue Life Framework
3.3. 3D Printing Approach
4. Results
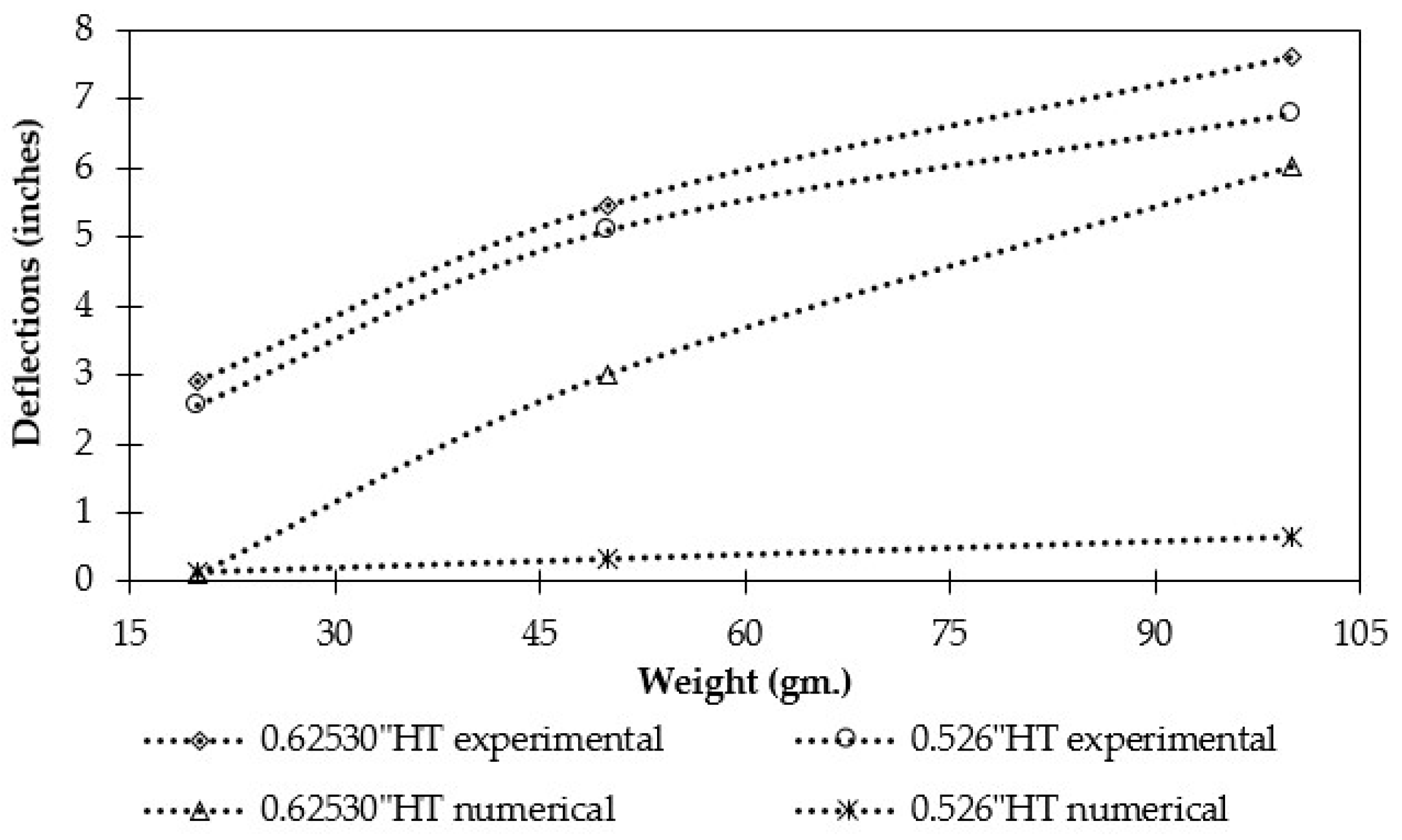
4.1. Fatigue Life Expectancy Against Different Deflections
4.2. Comparative Analysis of Prototype Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Pierre, M.S.; Mhlanga, S. Saskatchewan Continues to Live up to the Title of Breadbasket of Canada Canadian Agriculture at a Glance. Available online: https://www150.statcan.gc.ca/n1/pub/96-325-x/2021001/article/00008-eng.htm (accessed on 18 March 2024).
- Zeng, Z.; Martin, A.; Chen, Y.; Ma, X. Weeding Performance of a Spring-Tine Harrow as Affected by Timing and Operational Parameters. Weed Sci. 2021, 69, 247–256. [Google Scholar] [CrossRef]
- Pradel, M.; de Fays, M.; Seguineau, C. Comparative Life Cycle Assessment of Intra-Row and Inter-Row Weeding Practices Using Autonomous Robot Systems in French Vineyards. Sci. Total Environ. 2022, 838, 156441. [Google Scholar] [CrossRef] [PubMed]
- Chandel, N.S.; Chandel, A.K.; Roul, A.K.; Solanke, K.R.; Mehta, C.R. An Integrated Inter- and Intra-Row Weeding System for Row Crops. Crop Prot. 2021, 145, 105642. [Google Scholar] [CrossRef]
- Melander, B.; Liebman, M.; Davis, A.S.; Gallandt, E.R.; Bàrberi, P.; Moonen, A.C.; Rasmussen, J.; van der Weide, R.; Vidotto, F. Non-Chemical Weed Management. In Weed Research: Expanding Horizons; Wiley: Hoboken, NJ, USA, 2017; pp. 245–270. ISBN 9781119380702. [Google Scholar]
- Adigun, J.A.; Adeyemi, O.R.; Daramola, O.S.; Olorunmaiye, P.M. Response of Cowpea ( Vigna Unguiculata, L., Walp) to Inter-Row Spacing and Weed Competition. Agric. Trop. Et. Subtrop. 2020, 53, 73–79. [Google Scholar] [CrossRef]
- Alba, O.S.; Syrovy, L.D.; Duddu, H.S.N.; Shirtliffe, S.J. Increased Seeding Rate and Multiple Methods of Mechanical Weed Control Reduce Weed Biomass in a Poorly Competitive Organic Crop. Field Crops Res. 2020, 245, 107648. [Google Scholar] [CrossRef]
- Robinson, T.; Sussell, A.; Scott, K.; Poplin, G. Health Conditions among Male Workers in Mining and Other Industries Reliant on Manual Labor Occupations: National Health Interview Survey, 2007–2018. Am. J. Ind. Med. 2023, 66, 692–704. [Google Scholar] [CrossRef] [PubMed]
- Van Der Weide, R.Y.; Bleeker, P.O.; Achten, V.T.J.M.; Lotz, L.A.P.; Fogelberg, F.; Melander, B. Innovation in Mechanical Weed Control in Crop Rows. Weed Res. 2008, 48, 215–224. [Google Scholar] [CrossRef]
- Spaeth, M.; Schumacher, M.; Gerhards, R. Comparing Sensor-Based Adjustment of Weed Harrowing Intensity with Conventional Harrowing under Heterogeneous Field Conditions. Agronomy 2021, 11, 1605. [Google Scholar] [CrossRef]
- Tataridas, A.; Kanatas, P.; Chatzigeorgiou, A.; Zannopoulos, S.; Travlos, I. Sustainable Crop and Weed Management in the Era of the EU Green Deal: A Survival Guide. Agronomy 2022, 12, 589. [Google Scholar] [CrossRef]
- Tony Seskus. Farmers Seeking “right to Repair” Rules to Fix Their Own Tractors Gain White House Ally. CBC 2021. Available online: https://www.cbc.ca/news/business/biden-farmers-right-to-repair-1.6105394 (accessed on 8 February 2024).
- Pinke, G.; Giczi, Z.; Vona, V.; Dunai, É.; Vámos, O.; Kulmány, I.; Koltai, G.; Varga, Z.; Kalocsai, R.; Botta-dukát, Z.; et al. Weed Composition in Hungarian Phacelia (Phacelia Tanacetifolia Benth.) Seed Production: Could Tine Harrow Take Over Chemical Management? Agronomy 2022, 12, 891. [Google Scholar] [CrossRef]
- ASTM A229; Standard Specification for Steel Wire, Quenched and Tempered for Mechanical Springs. ASTM International: West Conshohocken, PA, USA, 2024.
- MatWeb Material Property Data. Available online: https://www.matweb.com/search/datasheet.aspx?matguid=417e182b8e9c42e7b84e437ee233908d&ckck=1 (accessed on 8 February 2024).
- Šarić, I.; Čolić, M.; Muratović, E.; Delić, M.; Muminović, A.J. Design and Development of Compression and Torsion Springs Using CAD/CAE. In Advanced Technologies, Systems, and Applications VI: Proceedings of the International Symposium on Innovative and Interdisciplinary Applications of Advanced Technologies (IAT) 2021; Springer: Cham, Switzerland, 2022; pp. 635–644. [Google Scholar]
- Böğrekci, İ.; Demircioğlu, P.; Ozer, G. Design and analysis of cost-effective compact disc harrow. Int. J. 3D Print. Technol. Digit. Ind. 2022, 6, 228–235. [Google Scholar] [CrossRef]
- Do, M.-H.; Nguyen, V.-T.; Omnes, P. Analysis of Dissipation Operators That Damp Spurious Modes While Maintaining Discrete Approximate Geostrophic Equilibriums for the B-Grid Staggered Scheme on Triangular Meshes. J. Comput. Phys. 2023, 489, 112261. [Google Scholar] [CrossRef]
- Ansys, R. ANSYS Mechanical APDL, Product Release 13.0; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Budynas, R.G.; Nisbett, J.K.; Tangcchaichit, K.; Shigley, J.E. Shigley’s Mechanical Engineering Design, 11th ed.; McGraw Hill Education: New York, NY, USA, 2021. [Google Scholar]
- Hasan, H.M.; Razzaq, H.Y.; Saleh, I.R. Machine Elements and Design Fundamental. In Proceedings of the Sixth International Scientific Conference for Iraqi Al Khwarizmi Society (FISCAS) 2020, Cairo, Egypt, 22–23 November 2020. [Google Scholar]
- Mohazzabi, P.; Shefchik, B.M. A Universal Relationship between Spring Constant and Torsion Constant. J. Phys. Chem. Solids 2001, 62, 677–681. [Google Scholar] [CrossRef]
- Miao, X.J.; Zhou, Z.T.; Zhang, Y.Y.; Yang, L.P.; Liang, X.; Wu, J.H.; Liu, C.R. A New-Type Lightweight Helical Elastic Metamaterial with Ultra-Low-Frequency Bandgaps. Phys. Status Solidi (b) 2023, 260, 2200355. [Google Scholar] [CrossRef]
- Nazir, A.; Ali, M.; Hsieh, C.H.; Jeng, J.Y. Investigation of Stiffness and Energy Absorption of Variable Dimension Helical Springs Fabricated Using Multijet Fusion Technology. Int. J. Adv. Manuf. Technol. 2020, 110, 2591–2602. [Google Scholar] [CrossRef]
- Yan, H.; Wen, B.; Wang, Z.; Zhu, C.; Ni, D.; Lin, M. Wear Analysis of Support Spring of Sprag Clutch during State of Overrunning. Math. Probl. Eng. 2022, 2022, 3417760. [Google Scholar] [CrossRef]
- A Co-Operative Program Between Evaluation Report 662 Phoenix Rotary Harrow; Alberta Farm Machinery Research Centre: Lethbridge, Canada, 1992; pp. 1–6.
- A Co-Operative Program Between Flexi-Coil System 90 (21.3 m) Harrow Packer Drawbar; Alberta Farm Machinery Research Centre: Lethbridge, Canada, 1982; pp. 1–5.
- Agarwal, D.K.; Razdan, A.; Agarwal, A.; Bhattacharya, P.; Gupta, A.; Kapoor, D. A Comparative Study of Orthodontic Coil Springs. J. Indian. Orthod. Soc. 2011, 45, 160–168. [Google Scholar] [CrossRef]
- Tan, P.S.; Farid, A.A.; Karimzadeh, A.; Rahimian Koloor, S.S.; Petrů, M. Investigation on the Curvature Correction Factor of Extension Spring. Materials 2020, 13, 4199. [Google Scholar] [CrossRef] [PubMed]


| Type | 0.62530” HT | 0.526” HT | |
|---|---|---|---|
| Physical Properties | Density | 7.80 g/cc | 7.80 g/cc |
| Mechanical Properties | Ultimate Tensile Strength | 1120–1300 | 1140–1340 MPa |
| Yield Strength Modulus of Elasticity | 1034 MPa 200 GPa | 1034 MPa 200 GPa | |
| Bulk Modulus Young Modulus | 160 GPa 190 GPa | 160 GPa 190 GPa | |
| Poisson Ratio | 0.29 | 0.29 | |
| Shear Modulus | 80 GPa | 80 GPa | |
| Thermal Properties | CTE, linear | 12 µm/m-°C | 12 µm/m-°C |
| Specific Heat Capacity | 0.470 J/g-°C | 0.470 J/g-°C | |
| Thermal Conductivity | 52 W/m-K | 52 W/m-K | |
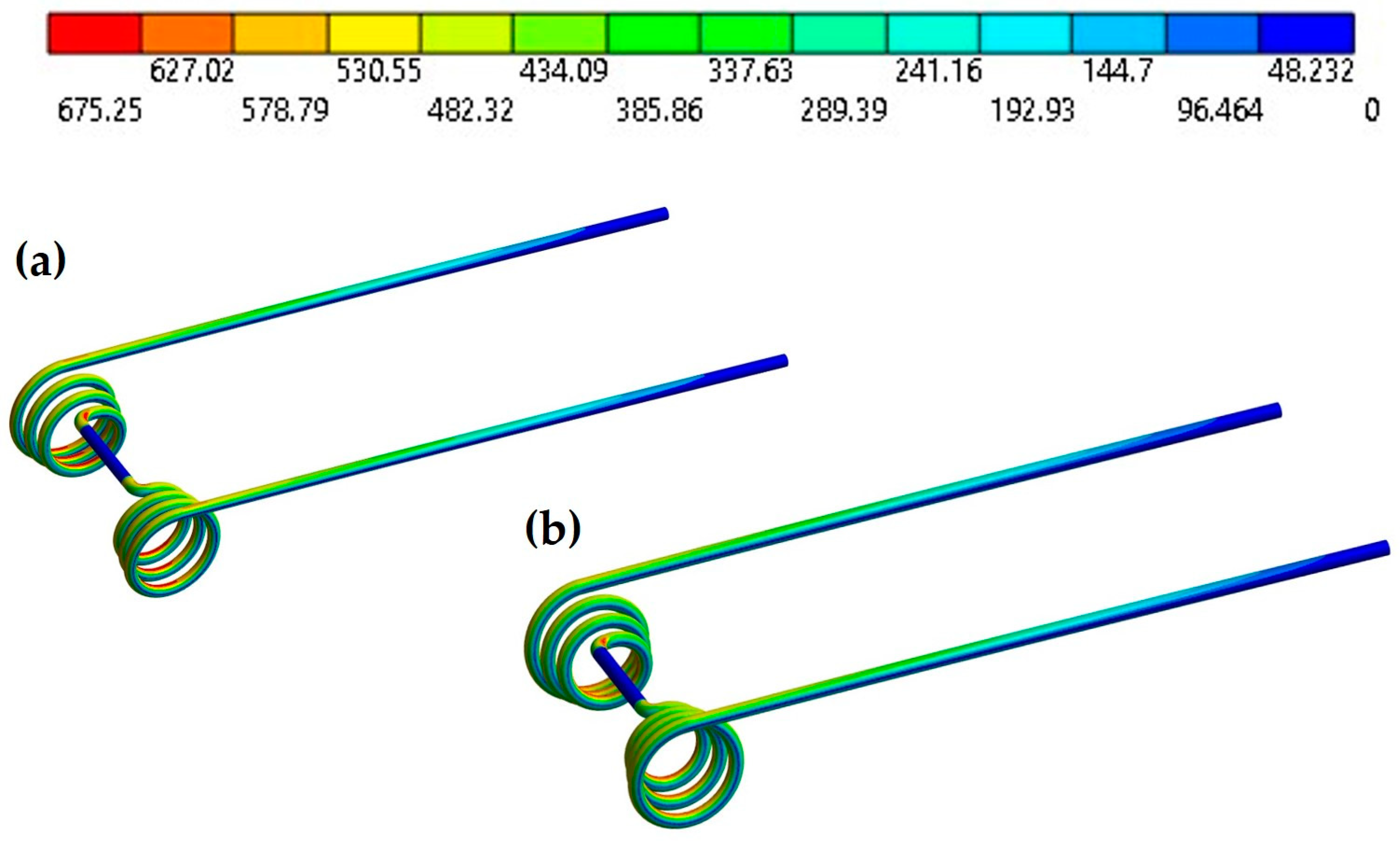
| Deflections (Inches) | Stress (MPa) | Life (Seconds) | Harrowing Capability (ha) | |||
|---|---|---|---|---|---|---|
| 0.62530” HT | 0.526” HT | 0.62530” HT | 0.526” HT | 0.62530” HT | 0.526” HT | |
| 12 | 675.25 | 667.23 | 25,425 | 28,873 | 117.66 | 133.62 |
| 10 | 562.71 | 556.03 | 65,653 | 67,807 | 303.83 | 313.79 |
| 8 | 450 | 444.82 | 1.7032 × 105 | 2.0855 × 105 | 788.21 | 965.12 |
| 6 | 337.62 | 333.62 | 6.973 × 105 | 7.9101 × 105 | 3226.94 | 3660.62 |
| 3 | 168.81 | 166.81 | >1 × 106 | >1 × 106 | >4627.77 | >4627.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.; Khondoker, M.A.H. Numerical Approach to Fatigue Life Prediction of Harrow Tines Considering Geometrical Variations. Eng. Proc. 2024, 76, 75. https://doi.org/10.3390/engproc2024076075
Rahman A, Khondoker MAH. Numerical Approach to Fatigue Life Prediction of Harrow Tines Considering Geometrical Variations. Engineering Proceedings. 2024; 76(1):75. https://doi.org/10.3390/engproc2024076075
Chicago/Turabian StyleRahman, Arafater, and Mohammad Abu Hasan Khondoker. 2024. "Numerical Approach to Fatigue Life Prediction of Harrow Tines Considering Geometrical Variations" Engineering Proceedings 76, no. 1: 75. https://doi.org/10.3390/engproc2024076075
APA StyleRahman, A., & Khondoker, M. A. H. (2024). Numerical Approach to Fatigue Life Prediction of Harrow Tines Considering Geometrical Variations. Engineering Proceedings, 76(1), 75. https://doi.org/10.3390/engproc2024076075







