Quantum Arithmetic for Directly Embedded Arrays ^†

Abstract

We describe a general-purpose framework to implement quantum algorithms relying upon an efficient handling of arrays. The cornerstone of the framework is the direct embedding of information into quantum amplitudes, thus avoiding hampering square roots. We discuss the entire pipeline, from data loading to information extraction. Particular attention is devoted to the definition of an efficient toolkit of basic quantum operations on arrays. We comment on strong and weak points of the proposed quantum manipulations, especially in relation to an effective exploitation of quantum parallelism. We describe in detail some general-purpose routines as well as their embedding in full algorithms. Their efficiency is critically discussed both locally, at the level of the routine, and globally, at the level of the full algorithm. Finally, we comment on some applications in the quantitative finance domain.

1. Introduction

Quantum hardware and software are still in their early days of development; thus, the design of quantum algorithms typically focuses on low-level operations. Although one should always keep in mind the hardware limitations, especially when describing possible near-term implementations of quantum algorithms, it is convenient to pursue higher levels of abstraction. Apart from its long-term and algorithmic interest, a more abstract and standardized approach serves practical purposes too, for example, that of making the benchmarking of quantum computer performances a more solid and transparent process. In turn, this helps pushing the research and the development in quantum computation at all levels. In the present paper, we describe a novel framework for the design of quantum algorithms on a more abstract plane. To this aim, we have three proposals [1].

2. Results

Our first proposal consists in the definition of a quantum matrix, namely a quantum state organized in two registers:

$$\left|\psi \right.⟩=\sum _{i=0}^{I-1}\sum _{j=0}^{J-1}{c}_{ij}{\left|i\right.⟩}_{n_I}\otimes {\left|j\right.⟩}_{n_J}.$$

(1)

Specifically, we interpret the first register as the index running over the rows and the second register as the index running over the columns. This way of storing the information has a common ground with that of Flexible Representation of Quantum Images (FRQI) and the Novel Enhanced Quantum Representation (NEQR) [2,3]. The main difference with FRQI and NEQR is that we encode the information of the (i,j) entry of the matrix in the quantum amplitude. Intuitively, the matrix is a bi-dimensional memory array where the amplitude encodes the information stored in the (i,j) memory location (see Figure 1).

Figure 1. Quantum matrix structure.

The second proposal is a key technical feature about how we encode the information into the quantum amplitudes, the so-called direct embedding [4]. Namely, the information to be stored into the quantum matrix is directly loaded into the amplitudes without taking square roots, as it is instead usually done in the literature. Such loading choice has several and important implications in later stages of the quantum algorithms and—most importantly—the information stored into the quantum state is handled and combined more easily, because algebraic operations are not hampered by the presence of square roots.

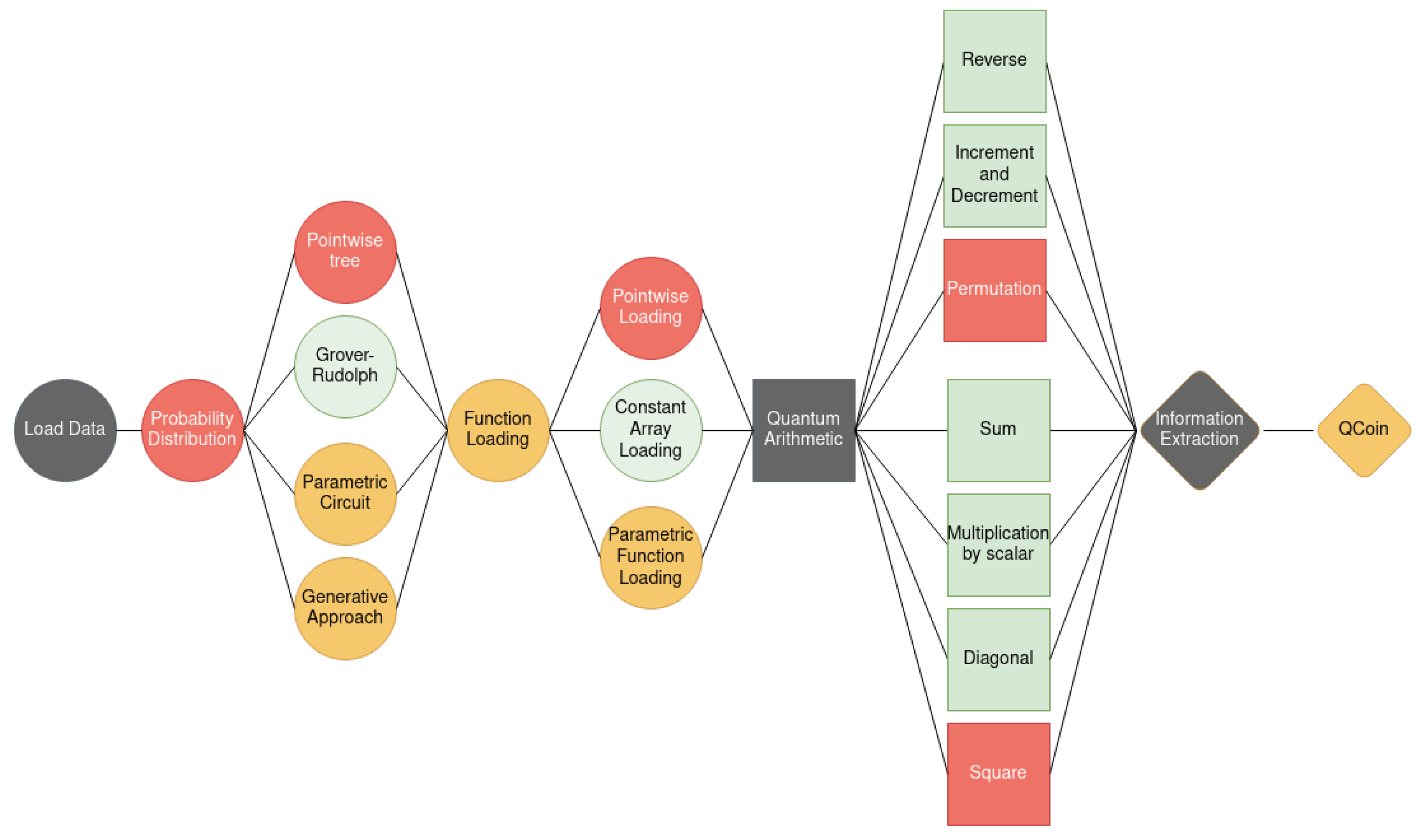
The third and final proposal is to give a full overview of the complete pipeline, or overall structure, of a generic algorithm admitting implementation within this framework (see Figure 2).

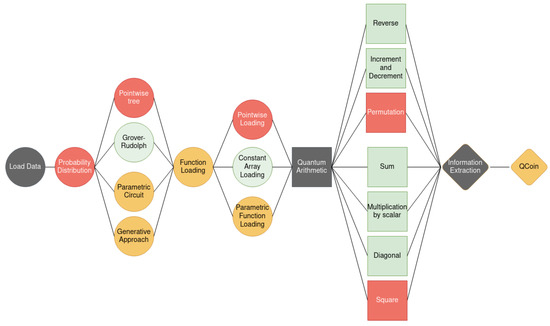
Figure 2. Structure of the pipeline. The dark gray nodes represent the three main steps; the nodes in red correspond to algorithms that are not efficient, for those in yellow the efficiency varies from case to case and, finally, the nodes in green represent efficient algorithms.

The first step of every algorithm corresponds to loading some input data. In the quantum case, it is often convenient to split this step into two sub steps:

• Loading a probability distribution [4,5,6];
• Loading a bi-dimensional function.

It is not strictly necessary to split the loading into two steps. Yet, we consider such splitting because—typically—we adopt different loading techniques for them: the probability distribution is loaded with a state preparation algorithm (e.g., a multiplexor binary tree); the function is loaded by means of another technique.

The second step of the pipeline in our framework corresponds to the implementation of various arithmetic operations, typically at the level of entire arrays or sub-arrays, and we refer to it as quantum arithmetic.

The third and last step of the pipeline corresponds to extracting the information that we have stored in the quantum state, namely the read-out of the state that encodes the result of the algorithm. There are multiple techniques for this purpose such as those appearing in [7,8,9,10,11].

3. Discussion

One of the advantages of organizing the pipeline as we have discussed is that it enjoys a modular structure; therefore, we can develop, analyze and improve each of the steps independently, achieving a better understanding of the problems in each domain.

In this paper, apart from introducing the framework, we provide some simple examples of arithmetic operations with finance in view. The possibility of implementing arithmetic operations has been considered in the literature since the early days of quantum computation. Apart from the quantum implementation of logical circuits corresponding to basic operations, such as the quantum adder [12,13], also the manipulation of “continuous” numbers has been studied. Let us mention some works which, at least in spirit, are closer to ours [14,15,16,17]. The difference with such approaches consists in the fact that we use a new embedding and organize the information into the matrix (1); these two aspects combined allow us to work in a transparent and simple manner.