Abstract
Currently, the number of common benchmark datasets that researchers can use straight away for assessing data-driven deep learning approaches is very limited. Most studies provide data as configuration files. It is still up to each practitioner to follow a particular data generation method and run computationally intensive simulations to obtain usable data for model training and evaluation. In this work, we provide a collection of datasets that includes several small- and medium-sized publicly available Water Distribution Networks (WDNs), including Anytown, Modena, Balerma, C-Town, D-Town, L-Town, Ky1, Ky6, Ky8, and Ky10. In total, 1,394,400 h of WDN data operating under normal conditions are made available to the community.
1. Introduction
Researchers and practitioners working in Water Distribution Network (WDN) analysis must face the challenges associated with data availability. Privacy, safety, and costs are the main cause of the aforementioned data limitation [1,2]. The earliest benchmark datasets aimed to facilitate the planning, design, and management of WDNs. Such datasets included the WDN topologies and the physical properties of the systems presented as configuration files. Those files serve as input to physics-based models that leverage mathematical tools to simulate the system’s hydraulics. Anytown [3] is one example among the first data contributions to the water research community. Later, the well-known C-Town dataset [4] was used in the “Battle of Water Calibration Networks”. Another important contribution in terms of WDN data is the Kentucky Research Database [5]. It includes data on 12 small and medium real WDNs in the state of Kentucky in the United States. These approaches provide a collection of configuration files that can be used for generating WDN data, but not the data themselves. The only work known that provides actual data is LeakDB [6], but the WDNs used in that work are very small (Net1: 10 nodes and Hanoi: 32 nodes). Moreover, the search space of the input parameters used in LeakDB is reduced to demand, and pipe rough coefficients, diameter and length, thus limiting the variability among the generated scenarios.
Recently, researchers in the water domain have turned to data-driven methods when performing WDN analysis. Several deep learning approaches have been used to solve a variety of problems, e.g., state estimation, leakage detection and localization, and water demand forecasting. Nonetheless, all of these methods are known to be data-hungry, i.e., they require vast amounts of data for model training. Those data requirements for training deep learning models expose the shortcomings associated with the existing datasets. First, the number of common benchmark datasets that can be used straight away for multi-task purposes is very limited. Second, existing data rarely include time-dependent patterns or a few patterns are overused by being assigned multiple times to different nodes.
In this work, we fill the data availability gap by providing a collection of datasets that includes several publicly available Water Distribution Networks. In the current version, our dataset contains small- and medium-sized WDNs including Anytown, Modena, Balerma, C-Town, D-Town, L-Town, Ky1, Ky6, Ky8, and Ky10. Following a modified version of the approach presented in [7], we generated ready-to-use data that represent stable states of 10 WDNs operating under normal conditions. In addition, we propose a demand pattern generation method that allows us to assign a different 24 h time-series demand for each individual node for all networks. As a result, 1,394,400 WDN states are provided. In addition, we provide a small version of the data that comprises 1000 scenarios per network with a total of 240,000 h of simulated data. The data provided enable researchers to address the following tasks: (i) state estimation, leveraging a limited number of sensors to reconstruct target measurements such as pressure, flow, and head; (ii) demand forecasting, with the goal of predicting customer demand within a given period; (iii) surrogate modeling, efficiently replicating the behavior of a simulation.
The remainder of this paper is organized as follows. Section 2 presents our dataset, describing the parameter selection and parameter boundary determination. Section 3 describes the most important characteristics of our dataset and how they differ from existing data benchmarks. Finally, in Section 4, we present the conclusions of our work.
2. Dataset Creation
In pursuit of enhanced generalization, the dataset extends the conventional simulation’s capability to untouched hydraulic-related parameters. The simulation is wrapped by a utility tool, the so-called WNTR [8]. The data generation method involves two phases: parameter selection and parameter boundary and sample quantity identification.
Parameter Selection: We collected several public WDNs from diverse regions. For each WDN, its relevant information (e.g., network topology, nodal elevation, demands, etc.) is compressed into an input (INP) file. We initiated by extracting all hydraulic parameters associated with every existing component, encompassing reservoirs, tanks, junctions, pipes, pumps, and various types of valves. It is worth noting that general information (name, coordinates, etc.) and quality-related parameters were omitted due to the lack of relevance in the scope of this study and the optimal storage matter. Afterward, a filtering approach alleviated irrelevant and redundant parameters from consideration. For example, a demand parameter was represented by base demand—a scaling scalar, and multipliers—a vector representing the demand pattern. In downstream applications, keeping both representations was unnecessary, resulting in only storing calculated demand values in the first-encountered parameter. In total, sixty hydraulic parameters were considered, and, after filtering, half of them were ready to use.
Parameter boundary and sample quantity identification: The next phase included the following steps: parameter boundary determination and sample quantity selection w.r.t WDN. The spectrum of input parameters in the pre-simulation stage is crucial for defining the data space. In essence, we utilized random sampling, which is a simple yet robust generation strategy, to synthetically generate numerous scenarios within the simulation. In light of this, the broader the parameter range, the more extensive the diversity.
In terms of demand, we automatically generated demand patterns by defining a consumption profile. The profile defined very low, low, mid, and high water consumption ranges. First, the day was divided into four 6 h segments starting at midnight. Then, the consumption ranges were randomly applied to the segments of a day, and using a periodic function, we extended these randomly generated patterns along the time axis to reach a specified duration.
To restrict outlier scenarios created by a corrupted set of parameters, we enforced several rules of validation. In particular, we targeted the pressure, one of the simulation outputs, and claimed its values in a range of [0, 151] [9]. Nevertheless, the restriction posed a significant challenge in finding optimal parameter boundaries for each WDN due to the massive search space. With an anticipated 100 scenarios, an arbitrary selection for each parameter frequently resulted in zero successful outcomes. As such, we designed a semi-automatic algorithm searching for an optimal configuration. For every parameter, the algorithm restricted values within a global data space crafted from available WDNs and then strategically selected discrete points along the max–min line. The criterion for evaluating the “goodness” of the selected values was the ratio of successful attempts out of 100 cases. By default, this acceptable ratio was set within the range of 40% to 60%. We noted that after multiple attempts without satisfying the essential ratio, the algorithm preserved the original value (if present) from the input file. This approach empowers practitioners to manually refine these parameters, fostering further study to discover the optimal configuration for each WDN.
Another consideration was the amount of created scenarios for each WDN. Each network varies in the number of nodes, edges, and topological complexity. As such, creating the same amount of samples for all WDNs could increase the burden of computational and storage units. Nonetheless, there exists no general rule for dataset size estimation. With this in mind, we empirically adopted a rule of 10, generating records in a quantity 10 times greater than the number of nodes within a WDN.
3. Discussion
In this section, we dive into the characteristics of the dataset provided. Figure 1 showcases the dispersion of pressure and demand data points between the baseline WDNs and the synthetic sets generated using our method. Within a valid pressure range, the baseline WDNs exhibit a concentration of points around 20 m, caused by the small values of demand (close to zero) in baselines. Such a situation can lead to instability in practical scenarios. While the baselines cover pressures from 20 to 100 m, our pressure data expand over a higher range, covering pressures up to 140 m. From Figure 1, it is clear that our dataset covers a much higher spectrum in terms of demand, contributing to the variety of the data. This variability is essential for training cutting-edge data-driven algorithms, providing adaptability and insight into diverse real-world scenarios.
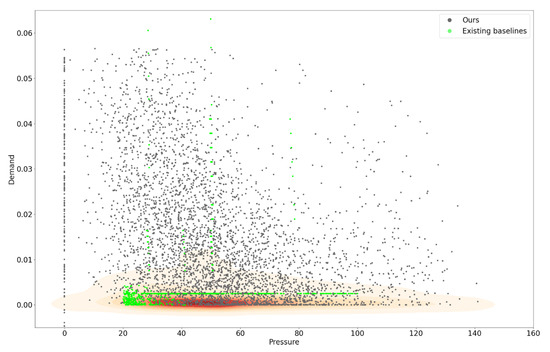
Figure 1.
Density distribution of pressure and demand of our generated data (gray) vs. the WDN baselines (green).
4. Conclusions
This study highlights the limited amount of ready-to-use data for WDN analysis, showing that existing data collections comprise mostly input configuration files for mathematical simulations. Researchers still need to run computationally intensive simulations and tweak existing data generation algorithms in order to obtain usable data. We provide a dataset of 50 gigabytes of compressed data which includes 1,394,400 WDN states operating under normal conditions. The data include all of the input parameters used for data generation, and the outputs obtained with the simulation tool WNTR, e.g., pressure, flow rate, velocity, head, etc. This work is, to the best of our knowledge, the first large-scale dataset that contains data that can be downloaded and used right away for different WDN analyses.
Author Contributions
Conceptualization, H.T., V.D., A.L and A.T.; methodology, H.T. and A.T.; software, H.T. and A.T.; validation, H.T. and A.T.; formal analysis, H.T.; investigation, H.T.; data curation, H.T. and A.T.; writing—original draft preparation, A.T. and H.T.; writing—review and editing, A.T., H.T., and V.D.; visualization, H.T.; supervision, V.D.; project administration, V.D. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the project DiTEC: Digital Twin for Evolutionary Changes in Water Networks (NWO 19454) and by NWO C2D and TKI HTSM Ecida Project Grant No. 628011003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The compact dataset associated with this study can be found using the DOI link (10.5281/zenodo.10974086). Given the external quota limit, we have made the larger dataset accessible through: https://drive.google.com/drive/folders/1nPO7qfOBAoUSRLozyqfaf7hxrBnFV-7g (accessed on 25 April 2024).
Acknowledgments
We thank the Center for Information Technology of the University of Groningen for their support and for providing access to the Hábrók high-performance computing cluster.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Brumbelow, K.; Torres, J.; Guikema, S.; Bristow, E.; Kanta, L. Virtual Cities for Water Distribution and Infrastructure System Research. In Proceedings of the World environmental and water resources congress 2007: Restoring our natural habitat, Tampa, FA, USA, 15–19 May 2007; pp. 1–7. [Google Scholar]
- Sitzenfrei, R.; Möderl, M.; Rauch, W. Automatic Generation of Water Distribution Systems Based on GIS Data. Environ. Model. Softw. 2013, 47, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Walski, T.M.; Brill Jr, E.D.; Gessler, J.; Goulter, I.C.; Jeppson, R.M.; Lansey, K.; Lee, H.-L.; Liebman, J.C.; Mays, L.; Morgan, D.R. Battle of the Network Models: Epilogue. J. Water Resour. Plan. Manag. 1987, 113, 191–203. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D. Battle of the Water Calibration Networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Jolly, M.D.; Lothes, A.D.; Sebastian Bryson, L.; Ormsbee, L. Research Database of Water Distribution System Models. J. Water Resour. Plan. Manag. 2014, 140, 410–416. [Google Scholar] [CrossRef]
- Vrachimis, S.G.; Kyriakou, M.S. LeakDB: A Benchmark Dataset for Leakage Diagnosis in Water Distribution Networks:(146). In Proceedings of the WDSA/CCWI Joint Conference Proceedings, Kingston, ON, Canada, 23–25 July 2018; Volume 1. [Google Scholar]
- Truong, H.; Tello, A.; Lazovik, A.; Degeler, V. Graph Neural Networks for Pressure Estimation in Water Distribution Systems. Water Resour. Res. 2024, 60, e2023WR036741. [Google Scholar] [CrossRef]
- Klise, K.A.; Hart, D.; Moriarty, D.M.; Bynum, M.L.; Murray, R.; Burkhardt, J.; Haxton, T. Water Network Tool for Resilience (WNTR) User Manual; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Paez, D.; Filion, Y. Generation and Validation of Synthetic WDS Case Studies Using Graph Theory and Reliability Indexes. Procedia Eng. 2017, 186, 143–151. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).