Optimization of the Steel Strip Heating Process by Changing the Excess Combustion Air ^†

Abstract

Reducing energy consumption and increasing energy efficiency have been especially topical issues recently, affecting all areas of energy consumption, including industrial sectors. Continuous annealing lines, as important industrial production facilities, operate with high energy consumption, which can be analyzed and optimized using predictive mathematical models. For the purpose of this paper, a mathematical model was developed to compare five variants of different excess combustion air operating with the same heat input and fuel consumption. The reference variant had an excess combustion air with a value of 1.279 and the steel strip temperature at the outlet of the heating chamber was 609.5 °C. In terms of energy savings, variant 1 can be considered as the optimal variant, which had an excess combustion air value of 1.15 and a steel strip temperature at the outlet of the heating chamber of 637.3 °C.

1. Introduction

Continuous annealing lines belong to the group of industrial furnaces that are used for the heat treatment of steel strips. The heating chamber is the greatest energy-consuming part of continuous annealing lines, and its heat source can be the combustion of fuels or the conversion of electrical energy into heat. When combusting fuels, it is important that a sufficient quantity of the oxidizing agent, which is oxygen or combustion air, is supplied to the fuel. The energy consumption of a continuous annealing line can be reduced by analyzing and optimizing the heating process of the steel strip in the heating chamber. Energy status analysis is the initial step for most areas of energy process control. Energy status optimization is aimed at finding a satisfactory solution in the field of energy processes. The optimization consists of numerous sub-processes, and the output of the optimization should offer a better solution than the current state and thus, it presents a process improvement. The predictive capability of mathematical models can be used to analyze and optimize the process of heating a steel strip in a heating chamber [1,2,3].

Mathematical models have an essential place in the field of automated process control systems. Based on their predictive capability, these models can predict the values of process variables or the processes’ histories, which enables efficient process control. A mathematical model is constructed from equations or mathematical means describing the state of the system under study. These equations are based on the fundamental laws of physics, chemistry, and biology, and may include simplifying assumptions. A properly constructed model can solve complex optimization problems. A necessary condition in mathematical modelling is the construction of an algorithm for the model [1,4,5].

2. Processing of Measured Data from the Continuous Annealing Line

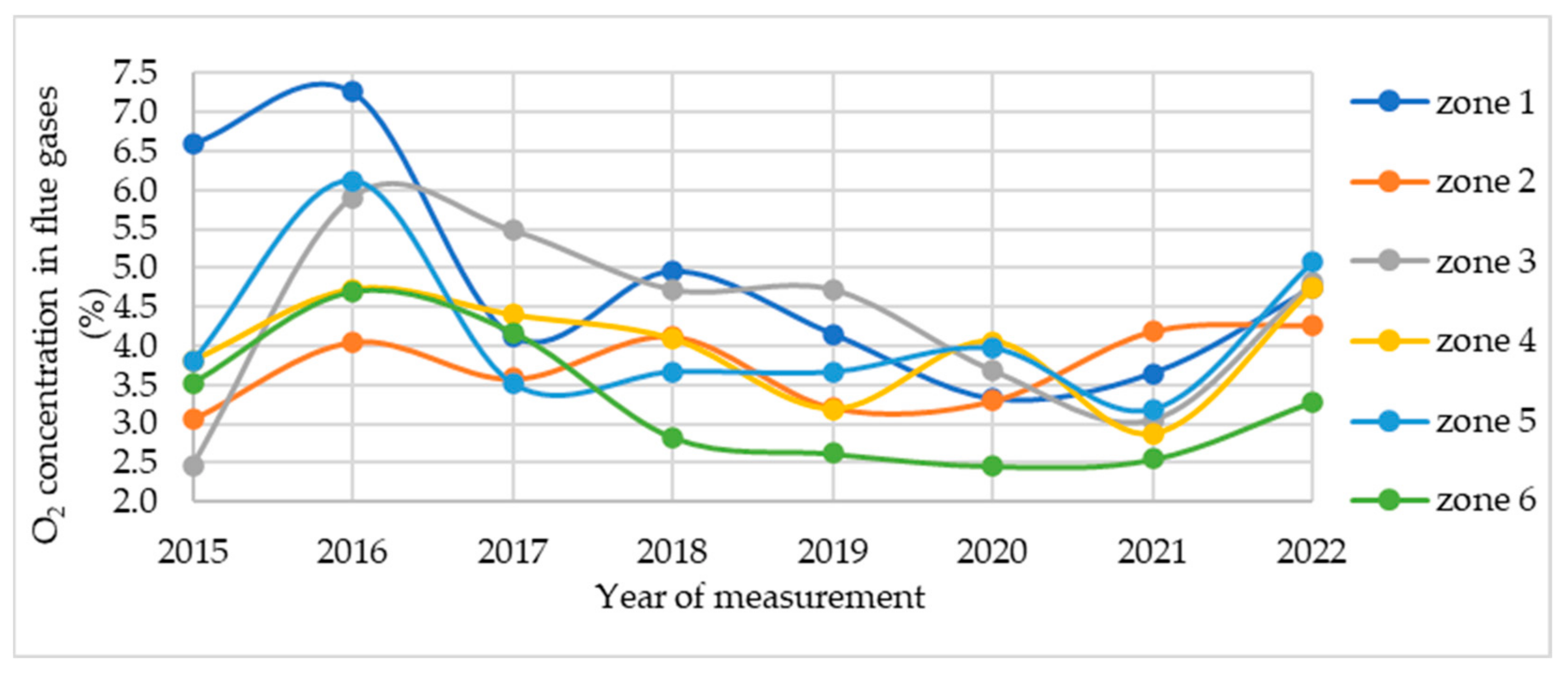
The observed object of measurement was the heating chamber of a continuous annealing line, and the analysis and optimization of the energy state was focused on the heating process of a steel strip in this heating chamber. This chamber is divided into six zones in which burners for the indirect heating of the steel strip are installed. From the measured data, the most processed steel strips of the same width, thickness, quality and at the same strip feed rate were selected.

One of the areas of the measured data processing was the adjustment of combustion ratios. Measurements of flue gas composition and O₂ concentration in the flue gas were carried out between 2015 and 2022. This O₂ concentration in the flue gas was uneven and the combustion process on the individual burners was carried out with different excess combustion air. In the case of high excess combustion air, some of the unused combustion air or O₂ took heat away from the outgoing flue gases, which consequently had a lower temperature. Therefore, less heat was transferred to the steel strip and, as a result, to heat the steel strip to the required temperature, fuel consumption had to be increased. The average values of the oxygen concentration in the flue gas for the individual zones of the heating chamber are shown in the graph (Figure 1).

3. Mathematical Model to Predict the Change in Excess Combustion Air

For a more detailed analysis of the energy state of the heating chamber and to find the possibilities of optimizing the heating process of the steel strip in the heating chamber, a mathematical model was created, which includes [1,2,4,5,6]:

• The geometric characteristics of the heating chamber;
• The course of the combustion process;
• The course of the strip’s stay in the heating chamber;
• The heat exchange in the heating chamber;
• The heat balance of the process in the heating chamber.

This mathematical model can also be used to predict the effect of a change in excess combustion air on the actual heating of the steel strip. The verification of this model relies on measured data from a real continuous annealing line [1,2,4,5,6].

Simplified mathematical model algorithm:

• Retrieval of the input and geometric data of the heating chamber;
• Start of the calculation of the parameters of the heating chamber;
• Definition of variables and estimation of individual parameters;
• Comparison of calculated and estimated parameters;
• Evaluation of the compared data;
• Selection of the optimal option or new estimation and repetition of the individual steps;
• The resulting heat balance.

4. Results from the Predictive Mathematical Model

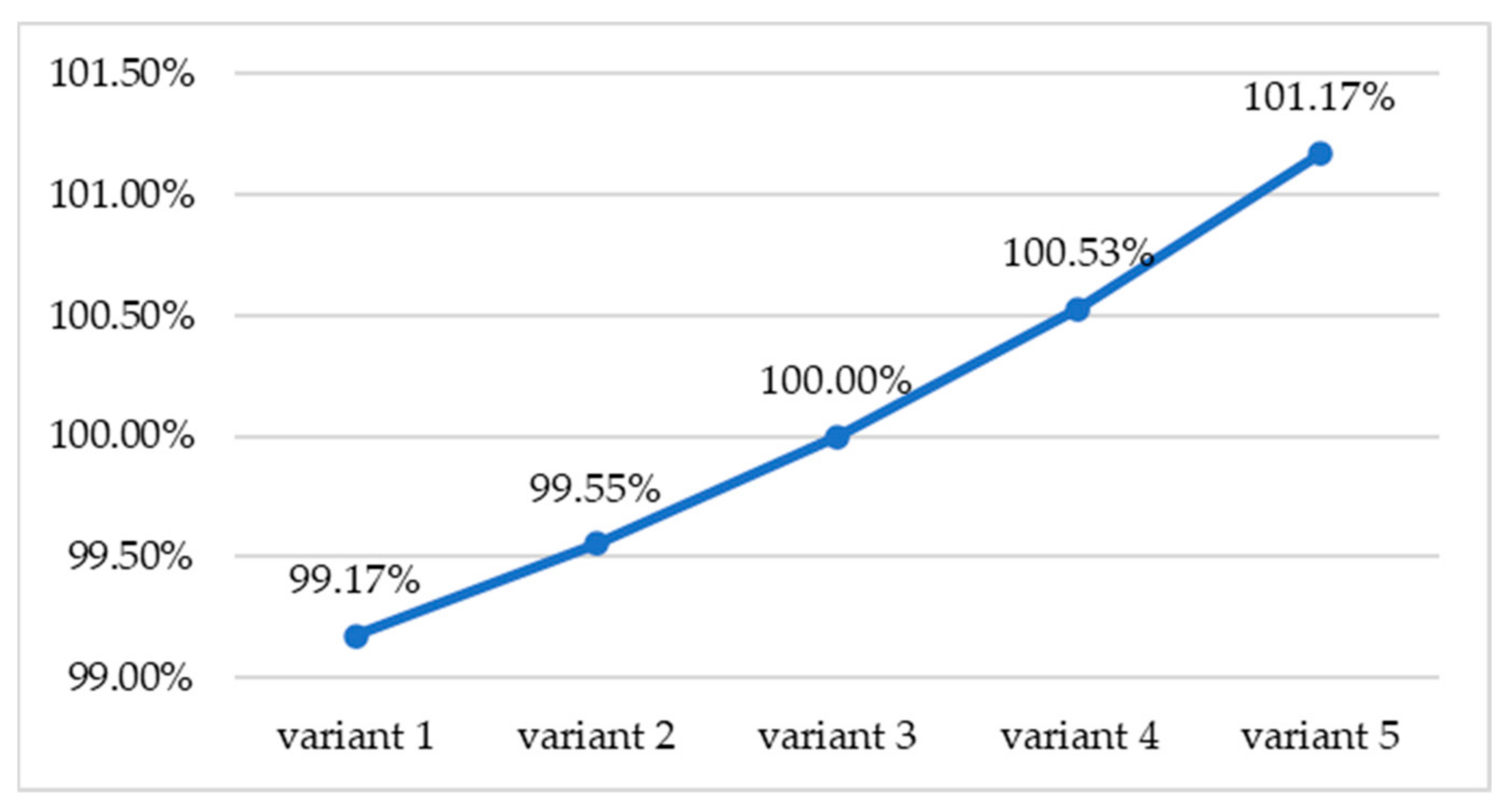
By using a mathematical model, it was possible to predict changes in heat exchange by defining a variable. In this case, the variable was the excess combustion air. The result of this modelling is the change in the strip temperature at the outlet of the chamber and the items making up the heat balance of the heating chamber. Based on these obtained values, it is possible to make a comparison of the different variants of the mathematical model and then select the optimal variant. The mathematical model solved five variants of excess combustion air, which are compared with the actual value, with variant 3 being the reference.

When the excess combustion air was changed with respect to the reference variant, heat accumulation occurred in the lining, which also had an impact on the change in the outlet temperature of the strip. When the product range is changed, the accumulated heat can be used or the lining must be reheated, which changes the specific fuel consumption for heating the strips. The heat accumulation in the lining itself also affects the internal surface temperature of the lining, which is involved in the heat exchange. In the case of a low lining temperature, part of the heat is consumed by accumulation in the lining, so that the heat input or fuel consumption needs to be increased to achieve the desired outlet temperature of the strip. Referring to this paper, the results of the mathematical model are considered after a steady state and hence the heat balance does not consider significant heat accumulation.

The table (

Table 1. Effect of excess combustion air on the outlet temperature of the steel strip.

Variant	Excess Combustion Air	O2 Concentration (%)	Strip Temperature (°C)
1	1.150	3.00	637.3
2	1.211	4.00	622.6
3	1.279	4.94	609.5
4	1.359	6.00	587.2
5	1.499	7.00	568.5

) shows the individual variants, with each variant being modelled with a different combustion air excess or O₂ concentration in the flue gas. The lowest modelled combustion air excess has a value of 1.15. In the case of a lower combustion air excess, the combustion process could result in the incomplete combustion of the fuel, which would produce harmful substances such as CO in the combustion process as well as represent fuel losses. This table also shows the change in the temperature of the steel strip at the outlet of the heating chamber relative to the reference variant.

In the table (

Table 2. Effect of excess combustion air on the amount of heat delivered to the heating chamber.

Variant	Chemical Heat (%)	Physical Heat (%)	Total (%)
1	92.92	7.08	100
2	92.57	7.43	100
3	92.16	7.84	100
4	91.67	8.33	100
5	91.10	8.90	100

), the resulting values of the heat balance of the heat supplied to the heating chamber are provided. Since the predictive mathematical model works with the same fuel consumption, then the amount of chemical heat delivered by the fuel is the same for all variants. The amount of physical heat delivered by the combustion air increases as the excess combustion air increases.

The graph (Figure 2) shows the effect of a change in the excess combustion air on the total amount of heat delivered to the heating chamber for the same fuel consumption. The reference variant represents 100% of the total heat delivered to the heating chamber, while the amount of heat delivered for the other variants varies only based on the amount of physical heat delivered by the combustion air.

Since the heat balance equation is based on the law of conservation of energy, then all the heat supplied to the heater must also be dissipated from it, and thus the dependence shown in the graph (Figure 2) also applies to the amount of heat extracted for each variant.

In the table (

Table 3. Effect of excess combustion air on the amount of heat dissipated in the heating chamber.

Variant	Steel Strip Heating (%)	Protective Atmosphere Heating (%)	Heat Loss—The Chamber Walls (%)	Heat Loss—Flue Gases (%)	Accumulation Heat (%)	Total (%)
1	56.23	1.56	4.21	37.89	0.02	100
2	54.12	1.56	4.14	40.16	0.08	100
3	52.22	1.55	4.06	42.46	−0.29	100
4	49.22	1.55	3.95	45.25	0.15	100
5	46.74	1.54	3.84	47.91	0.02	100

), the resulting values of the heat balance of the heat dissipated from the heating chamber are recorded. When the excess combustion air in the combustion process decreased, less flue gas was produced and thus the flue gas reached a higher temperature. The flue gas subsequently heated the burner surface for indirect heating. The higher the temperature of the burner surface, the more intense the heat transfer in the heating chamber, which can be observed in the results of the heat consumed to heat the steel strip and the losses through the chamber walls. Conversely, as the excess combustion air increases, the combustion process produces more flue gases, which consume more heat and consequently have a lower temperature. As a result, the heat transfer is not as intense and the outgoing flue gases dissipate a large amount of heat to the atmosphere, which represents a significant energy loss.

The results of the mathematical model show that when the excess combustion air value is reduced to 1.15, or when the O₂ concentration in the flue gas is reduced to 3%, it is possible to achieve an increase in the outlet temperature of the steel strip by almost 30 °C, while the heat input is the same as in the case of the reference variant. Hence, it is possible to reduce the fuel consumption while maintaining the steel strip outlet temperature defined by the reference variant.

5. Conclusions

In an effort to reduce the energy consumption of the continuous annealing line, the first step was to analyze the current energy status of the heating chamber. The necessary data measurements were taken, which were then processed and evaluated. Using a predictive mathematical model under the conditions of a continuous annealing line, the sources contributing to an increase in fuel consumption when heating a steel strip at the same geometry and strip feed rate were determined. Excess combustion air is considered to be one of the most significant influences on fuel consumption during strip heating. A predictive mathematical model was used to predict the effect of the change in combustion air excess on the actual heating of the steel strip. The verification of this model was based on the measured data from a real continuous annealing line. The mathematical model compared five variations of different excess combustion air, with all variations operating at the same fuel consumption. Using a predictive mathematical model, it was found that when the excess combustion air drops to a value of 1.15, the outlet temperature of the steel strip is 637.3 °C, which is almost 30 °C higher than the reference variant, which has an outlet strip temperature of 609.5 °C with an excess combustion air value of 1.279. The results show that higher temperatures of the steel strip at the outlet of the heating chamber can be achieved with lower excess combustion air. By modifying the mathematical model, it is possible to build a model that will model the fuel consumption for the desired steel strip temperatures due to the change in excess combustion air.