Traffic Signal Control System Using Contour Approximation Deep Q-Learning ^†

Abstract

A reliable transit system is essential and offers a lot of advantages. However, traffic has always been an issue in major cities, and one of the main causes of congestion in these places is intersections. To reduce traffic, a reliable traffic control system must be put in place. This research sheds light on how to consider dynamic traffic at intersections and minimize traffic congestion using an end-to-end deep reinforcement learning approach. The goal of the model is to reduce waiting times at these crossings by controlling traffic in various scenarios after receiving the necessary training.

1. Introduction

Over time, there has been a rise in the number of people moving around, which has led to an increase in traffic. Numerous negative effects of increased traffic include longer travel times and higher pollution levels brought on by the increased fuel consumption of cars. Currently, a traditional, three-phase, pre-timed signal system that includes red, yellow, and green phases is employed.

This signaling system works with a set duration based on the provided timings. This approach, however, does not account for the dynamic traffic that moves through each lane at intersections.

There is ongoing research being conducted to provide new approaches to the problem of traffic congestion. Numerous approaches are now being used to address this issue as a result of the technology sector’s rapid growth [1,2]. One such instance is the Internet of Things [3,4] where traffic is efficiently controlled using cameras and other sensors. Wireless sensor networks (WSN) [5] and the use of embedded platforms [6] are two more effective techniques.

However, the fields of artificial intelligence and machine learning have given rise to many methods which are effective in controlling traffic. Reinforcement learning (RL) is a practical method for controlling traffic signals [7]. The use of deep reinforcement learning [8], which introduces a feature-based state representation and rewards idea, is one example among many.

This technique makes TSC scalable. The deep convolutional neural network [9] used in this technique, which also uses deep reinforcement learning, collects parameters from the raw traffic data, such as the locations, speeds, and waiting times of the cars.

In this paper, we present a traffic control system that takes images of traffic intersections with dynamically flowing vehicles as the input and performs traffic signaling. The model’s objective is to decrease the average waiting time at crossings while also identifying emergency vehicles and opening the lane in which they are traveling to give them top priority. We run the model on different scenarios and compare it with other proposed traffic signal control systems.

The contributions of this paper are as follows:

1. We propose an off-policy end-to-end deep reinforcement learning [10] based traffic signal control system to control dynamic traffic efficiently at intersections with top priority for emergency vehicles.

2. The model proposes detecting emergency vehicles on any of the sides of the intersection and aims to reduce their waiting time by clearing the traffic in that lane.

2. Related Work

Several other machine learning models that have been used to propose a traffic signal control system are studied here.

A deep reinforcement learning model is created in [11] to control the traffic light cycle. By compiling the traffic patterns, the complex traffic situation in the United States is assessed. Small grids are used to divide up the entire traffic intersection. In this model, states, rewards, and actions are all used.

Using a Gaussian convolutional neural network is an alternative strategy. A graph convolutional neural network is developed in [9]. Agents are established in a distributed manner to design a policy to run a traffic signal at an intersection using the recommended method as opposed to speaking to other agents directly. The suggested method can locate comparable policies using an FCNN twice as fast as the conventional RL-based method, and it is also better equipped to handle variations in traffic demand. In the context of six crossings, the outcomes of NFQI employing the GCNN, FCNN, and fixed-timing control were compared.

Chen et al. [12] utilized a five-layered convolution with a (2 × 2) filter size without a pooling layer. The unique method used by the authors (PCNN) involved simulating periodic traffic data using deep neural networks based on convolution. The study folded the time-series to create the input, which incorporated historical and real-time traffic data. They replicated the amount of congestion from the previous time slot in the matrix to illustrate the relationship between a new time slot and the recent past.

Convolution neural networks are suggested as a possible implementation of the traffic sign recognition method by Shustanov et al. [13]. The paper also shows alternative CNN designs side by side for comparison. The TensorFlow library and CUDA’s massively parallel architecture for multithreaded programming are used to train the neural network. On a mobile GPU, the full detection and recognition procedure for traffic signs is carried out in real time.

The author used TensorFlow, a deep learning framework, to tackle the identification of traffic signs issues. Training and testing were carried out on the GTSRB dataset.

Modern reinforcement learning (RL) techniques for online signal controller optimization were put forth by Mousavi et al. [14]. In this way, the set of approaching vehicles (incoming lane, speed, waiting time, queue length), as well as the present signal assignment (enabled phase), frequently determine the status of the intersection. An RL agent must optimize a technique that links state mapping to signal (phase) assignment. Deep Q-learning techniques are frequently used for this type of learning with the goal of learning the projected future value from each action in a particular state. The controller is then told to take the best steps it can going forward.

Table 1 shows the comparison of different reinforcement learning methods.

Table 1. Different reinforcement models.

Sl No.	Year	Reinforcement Method Used	Working	Applications
1	2020	Model-based Monte Carlo	Utilises sampling to estimate the Markov decision process dynamics.	Used in situations where there are a lot of data to process. There is a guarantee that the estimations will be quite accurate.
2	2018	Policy-based gradient	The policy gradient-based method directly learns from the policy rather than modeling the value function.	Utilized in autonomous vehicle design where the state consists of convoluted situations provided to agents.
3	2018	Actor critic	The actor critic technique estimates and updates both the policy and value functions.	There are many actor critic methods such as A2C that are used in autonomous driving.
4	2019	Q Learning	It is a temporal difference method, an off-policy method where a Q- value is estimated to optimize the actions.	It is used extensively in training agents to play games and has been proven effective in being able to learn complex rules.
5	2017	Deep reinforcement Learning	It employs neural networks that do not explicitly specify the characteristics; instead, they use the state as input the directly.	It is utilized in tasks where the state is not easily representable, such as tasks where the screen itself acts as a state.

3. Problem Definition

In this section, we define the problem statement for our traffic signal control system.

Consider a single crossroads where traffic flows in all four directions. Traffic signals are used to indicate whether or not vehicles in a lane are allowed to proceed or must halt. We consider STOP (indicated by a red light) and GO (indicated by a green light) as the two possible states for the signal in order to keep things simple. We adhere to left-hand traffic laws, but this has no impact on the model, which can be adjusted to operate under right-hand situations as well.

The transitions for the signal are indicated below. Following the same method mentioned in the above paragraph, four different states are possible.

1. Signal 1 is green, and the rest are red

2. Signal 2 is green, and the rest are red

3. Signal 3 is green, and the rest are red

4. Signal 4 is green, and the rest are red

The intersection can be modeled using a Markov decision process. It provides a mathematical framework for representing environments in reinforcement learning applications. [10] For our application, we define a quadruple MDP (Markov decision process) to represent the environment as follows:

< St, At, Rt+1, St+1 >

(1)

where St represents the current state, At represents the action taken by the agent, St+1 is the state reached when action At is taken at state St, and Rt+1 is the reward for taking action At at St and reaching St+1.

4. Traffic Signal Control Design

In this section, we introduce the different aspects of the proposed model, such as the environment, reward, and actions.

4.1. Environment

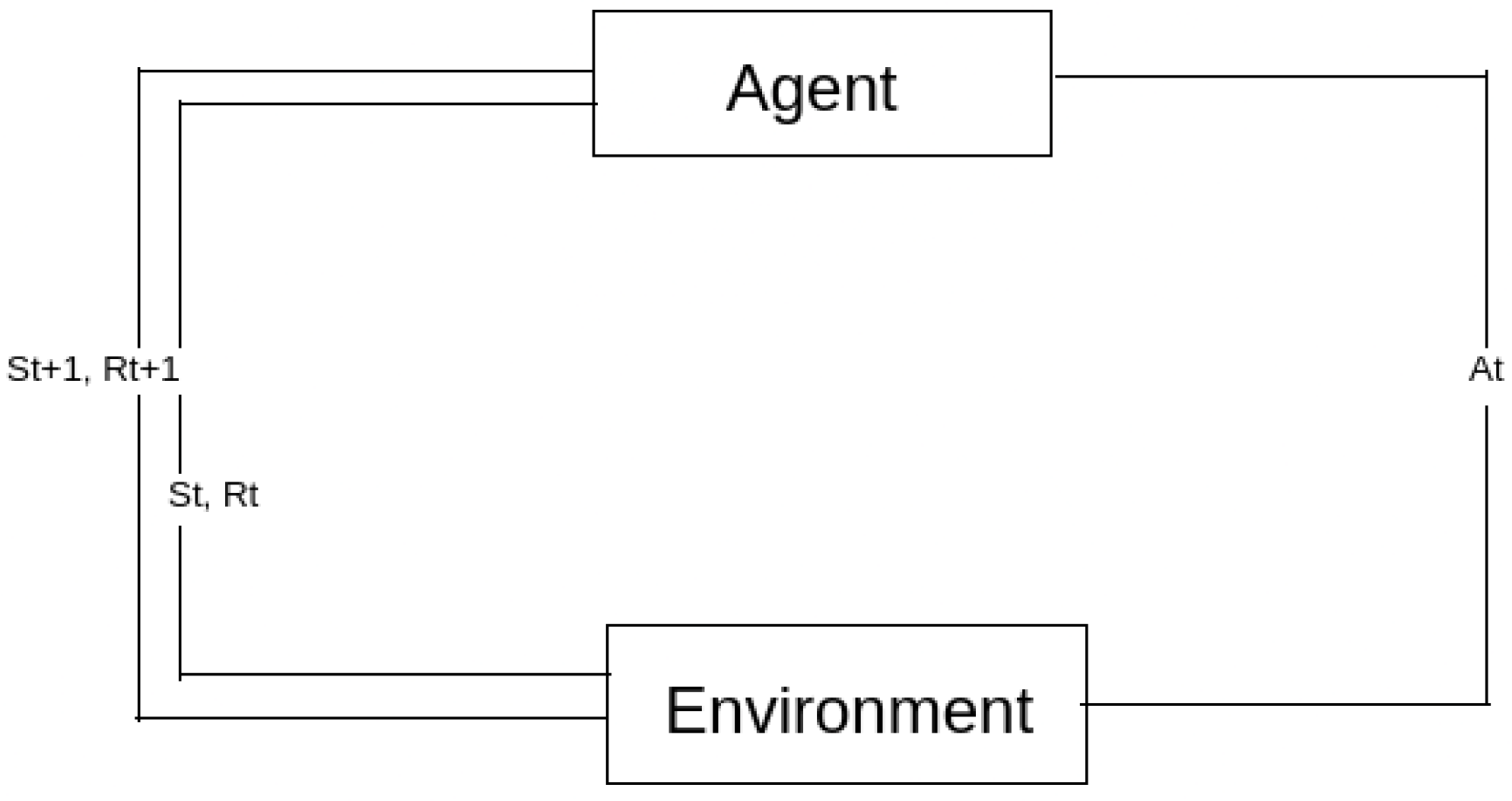
Figure 1 represents the environment where we conduct our experimentation. A surveillance camera placed at the crossroads allows us to record the status as seen in this context. Since these data are essential for instructing the RL agent, the camera should be set up so that it can adequately watch traffic from all four lanes.

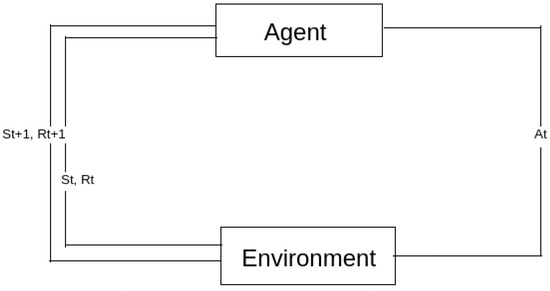
Figure 1. Interaction between agent and environment.

4.2. Reward

Since the main goal of this experiment is to minimize the average waiting time at junctions, this parameter can act as a good reward. The average waiting time is calculated by summing up the waiting time (time between stopping at red light and starting at green light) of each vehicle in every lane and then dividing by the total number of vehicles. Once we have obtained the average waiting time, we need to consider the negative of this number as a reward. This is because the reward acts as a positive signal for our RL agent and it is trying to maximize the reward. While this approach is simple, it can also increase the complexity of computation, as the average waiting time can become a very large number in the case of heavy traffic.

4.3. Actions

The agent can take four given actions at any given time, i.e., make any one of the four signals green and the rest stay red. This is a simplified version of the actual way that signals work in reality, as yellow lights are used to ask vehicles to slow down. However, since the duration of yellow lights is constant, it is not something complex enough to be learned by our agent. However, we can train our agent in these four actions, and it will still be able to work in environments which use yellow lights, because that depends on the design of the environment and does not affect the learning curve of the agent.

5. Algorithm

The algorithm of the Q-network is presented in Algorithm 1. The algorithm works by first obtaining the state at any time t. It can then take one of two paths—one path chooses to “explore”, i.e., choose a random action, and the other path chooses “exploitation”, i.e., it chooses an action based on the Q-value output of the Q-network. Once the action is sent to the environment, the rewards and the next state are received. These values are then used to fit the Q-network. This process takes place infinitely and the Q-network is eventually able to converge on the policy.

Algorithm 1

while t ← 1toN do s = getState() a = 0 ε = εo − t if rand(0, φ) ⟨ ε then a = rand(0, 4) else probs = CA DQN(state) a = max(probs) end if send action to env() r = receive reward() s’ = getState() target = copy(Q-network) calculate Q-value targetNetwork.Q-value = calculated Q-value loss = MSELoss() optimizer = Adam() add tuple into replay buffer if t%Ω = 0 then sample BRB tuples from replay buffer target = copy(Q-network) for BRB tuples sampled do calculate Q-value targetNetwork.Q-value = calculated Q-value loss = MSELoss() optimizer = Adam() end for end if end while

6. Handling Emergency Vehicles

Once we have trained an effective object detection algorithm, the idea is to narrow down the lane that has the maximum number of emergency vehicles at that timestep and free up that lane.

A disadvantage of this approach is that we will not be taking the magnitude of the emergency of the vehicles into account, but the only way of knowing this would be if the vehicles themselves transmit information to our algorithm, which cannot be expected of all vehicles.

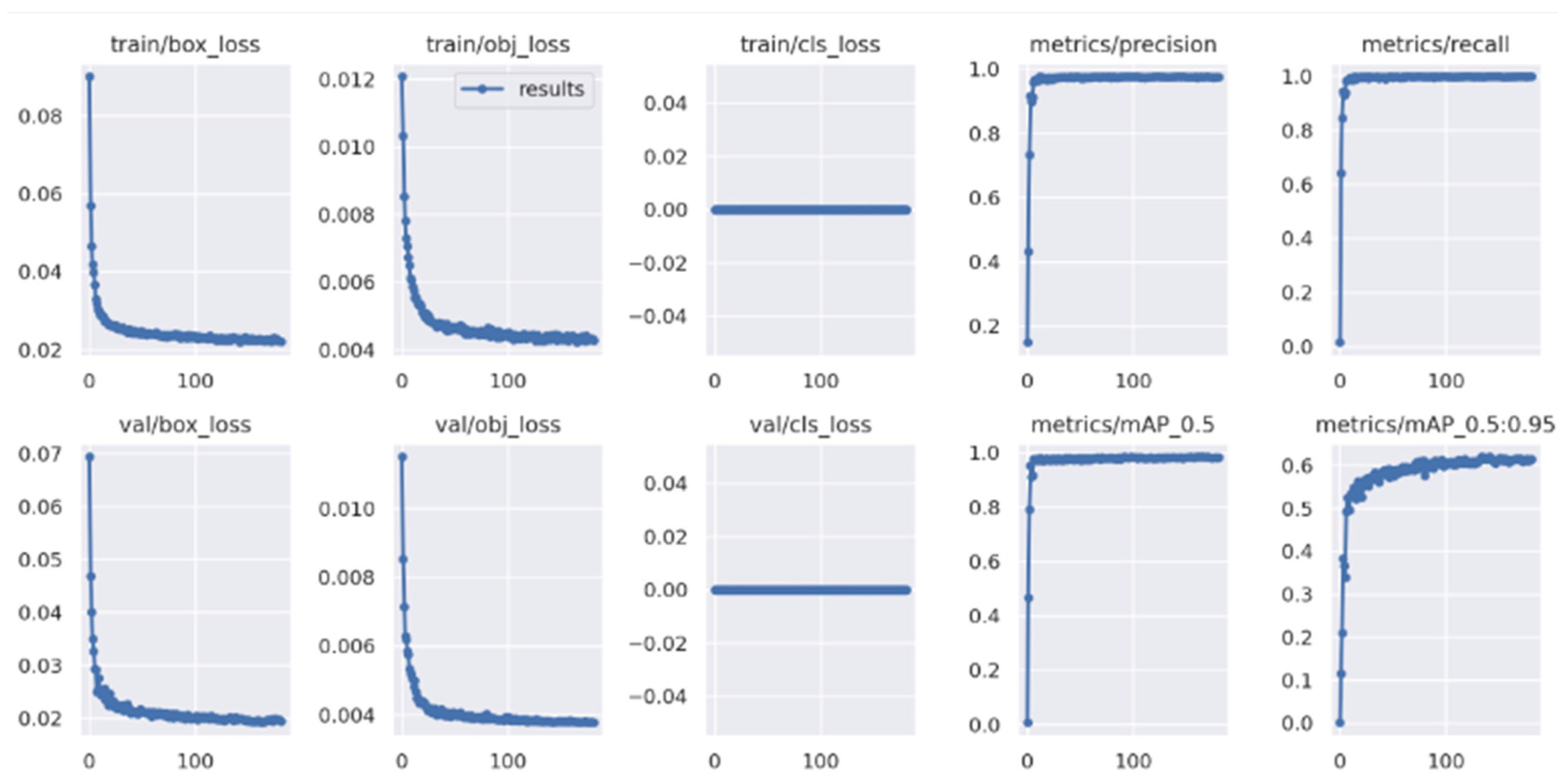
Our algorithm will, however, ensure fairness by selecting a random lane among the lanes with the maximum number of emergency vehicles, if there is a deadlock. For the purpose of addressing emergency vehicles, we use YOLOv7. YOLOv7 is currently the latest architecture [15] of the popular You Only Look Once object detection algorithm that is capable of predicting better bounding boxes at a high speed. Training results are shown in Figure 2.

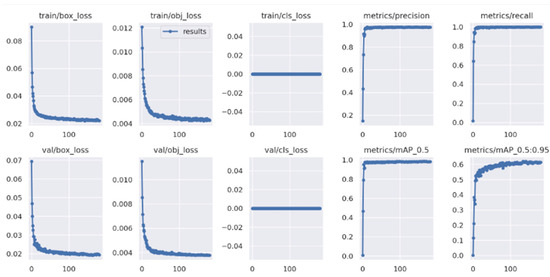
Figure 2. Training results of YOLOv7 model.

7. Results

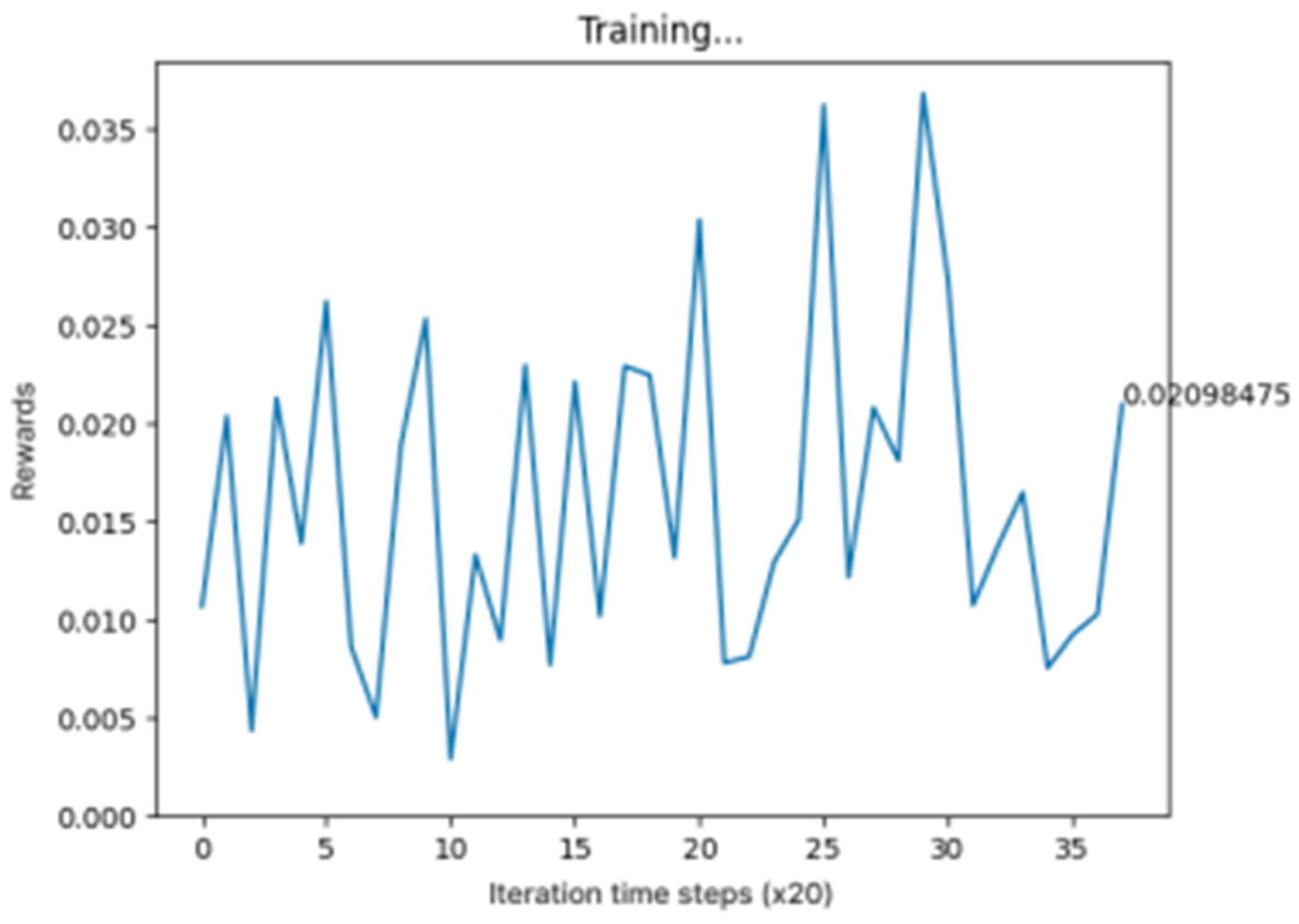
Figure 3 shows a graph of the training results which represent the average waiting time of vehicles for our model.

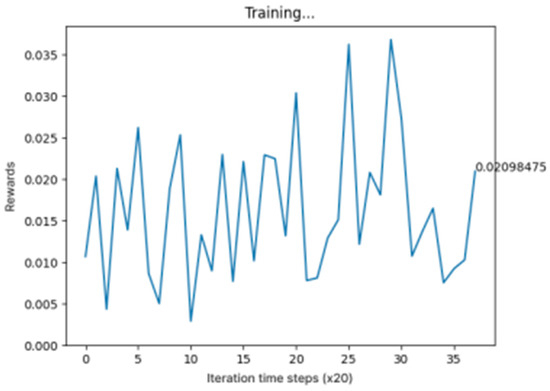
Figure 3. Training results of CA-DQN model.