Design and Implementation of Hardware-Implemented Dual-Axis Solar Tracking System for Enhanced Energy Efficiency †
Department of Electrical Engineering, School of Engineering & Technology, Poornima University, Jaipur 303905, Rajasthan, India
*
Author to whom correspondence should be addressed.
†
Presented at the International Conference on Recent Advances in Science and Engineering, Dubai, United Arab Emirates, 4–5 October 2023.
Eng. Proc. 2023, 59(1), 122; https://doi.org/10.3390/engproc2023059122
Published: 27 December 2023
(This article belongs to the Proceedings of Eng. Proc., 2023, RAiSE-2023)
Abstract
:This paper concentrates on the development of a closed-loop tracking of the sun that precisely follows the sun’s trajectory, allowing photovoltaic panels to capture the maximum amount of solar energy. Azimuthal and elevation-tracking mechanisms are included in the proposed system, and a feedback controller based on sensors monitors the brightness of the sun continuously as a reference signal. The controller generates a signal to operate the tracking motor with two axes, orienting the PV panel towards the sun, when the intensity exceeds a set threshold. In both east–west (E-W) and north–south (N-S) directions, the solar tracking system (STS) tracks the sun’s position independently. A dual-axis solar tracking system (DAST) was made of three 335-watt panels (each generating 1 kilowatt of power) in a PV system. Three 335-watt panels were used to successfully execute the dual-axis solar tracking system, with each panel contributing to the PV system’s overall power generation of 1 kilowatt. Overall, the PV system integration of a dual-axis solar tracking system with three 335-watt panels shows the potential for higher power output and energy efficiency. This configuration offers a viable means of maximizing the advantages of renewable energy sources and efficiently harnessing solar energy.
1. Introduction
Through the use of PV cells, solar photovoltaic (SPV) technology transforms sunlight directly into electrical energy. Due to its ability to supply sustainable and clean energy, this technology has recently grown in favour. Due to its renewable nature and lack of harmful emissions, solar energy is an appealing choice for lowering the emissions of carbon dioxide output and halting climate change [1]. In India, the days are relatively long and sunny for more than ten months, with only two months (December and January) of partial cloud cover. As a result, solar energy is incredibly plentiful in our country. The volume of SPVs in India expanded by over 40 times during the previous three years [2].
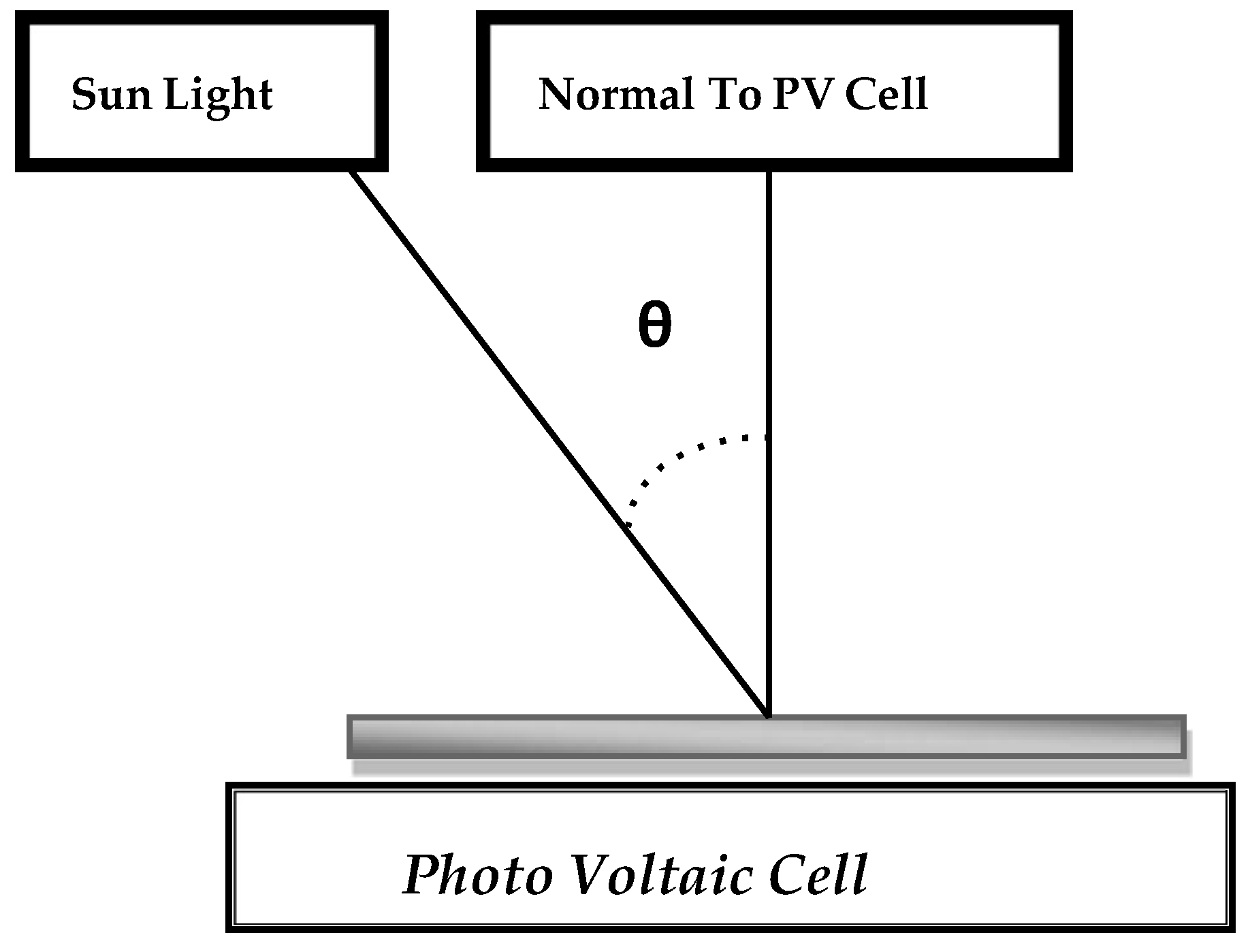
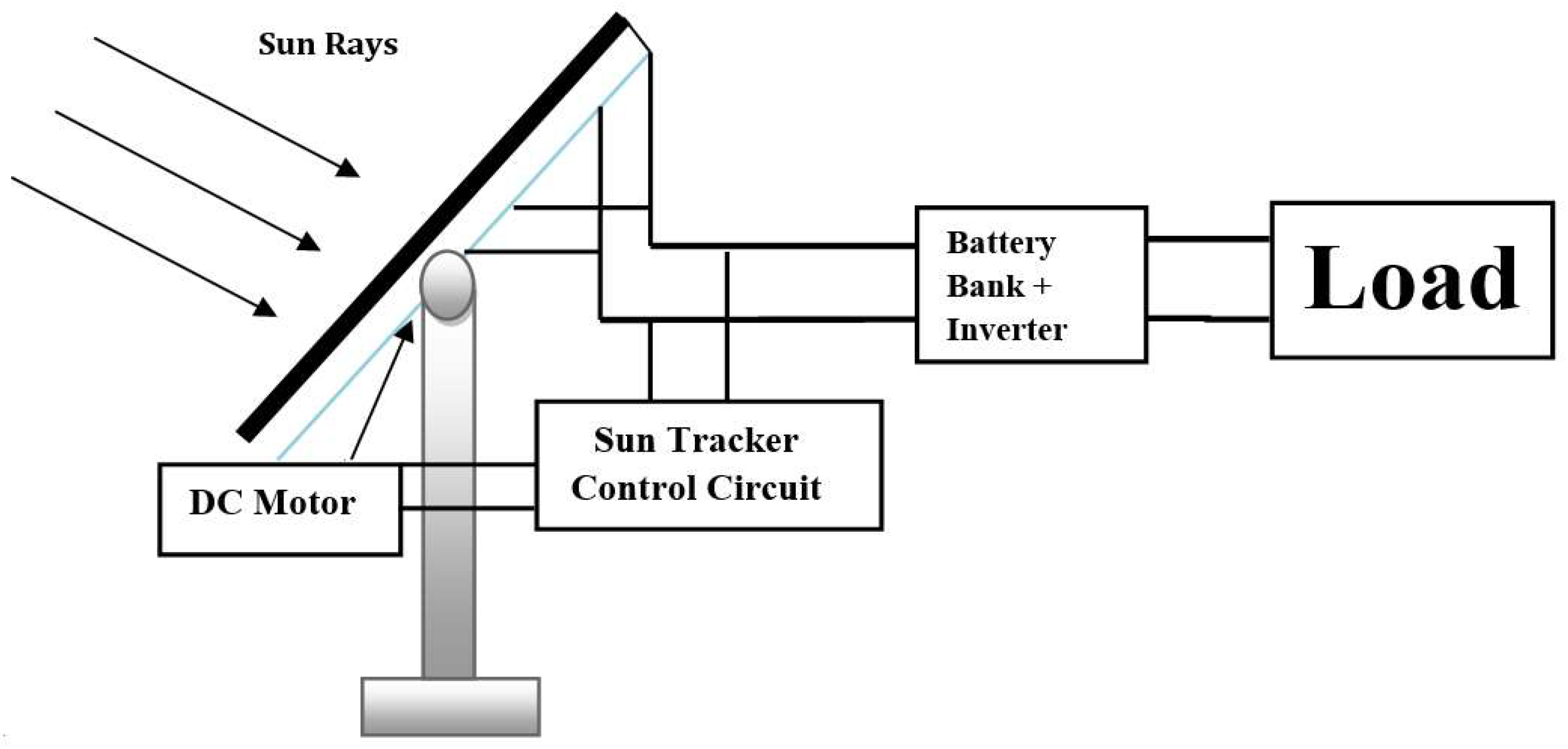
2. Requirement of Tracking System
The fact that the sun’s position changes throughout the day and year necessitates the use of a sun-tracking system. Solar panels or solar collectors are used because being installed in one place does not provide enough sunlight to generate maximum energy. By tracking the motion of the sun through the sky, a sun-tracking system can keep solar panels or solar collectors oriented towards the sun, maximizing the amount of sunlight received and thus increasing energy output [3].
Direct current (DC) is produced by PV cells. As a result, cells and panels can both be thought of as DC sources. The current value that is generated is based on how much light the PV panels are absorbing. Figure 1 illustrates how a tracker system improves the PV system’s efficiency, allowing the Sun to be at an angle with respect to the panel axis. Regular sunlight is defined by its incidence angle. The quantity of electricity generated (W) can be calculated using the following formula assuming that the sunshine is strong [3].
𝑊 = 𝐴𝜆𝐶𝑜𝑠𝜃
PV cells are installed in area A in this particular instance. To maximise the power produced by PV cells, the tracking system aims to maintain the angle close to zero.
The experiment made use of a prototype of the institute’s rooftop that was fitted with a tracking system. The objective of the experiment was to investigate how changes in the angular position of the fixed panel influenced a number of various metrics, including the tracking device’s effectiveness, wind pressure, and current in the static system. The trial examined the tracking device’s efficiency throughout the day [4]. By analysing the trial results, critical understanding could be obtained into the tracking system’s conduct in various situations and identify potential development areas. The results of this experiment may be used to improve the STS model and other applications, such as solar panels and wind turbines, that call for precise and effective orientation with regard to environmental factors [5].
For the closed-loop tracking approach, the problem of solar tracking is to determine the optimal PV panel orientation (output) to receive maximum sunlight (input). The whole system comprises a Solar Tracker PV system, LDR, DC motor, battery bank, and tracker control circuit. In the tracking operation, the LDR sensors placed at different positions on the sun tracking stand measure the sunlight intensity [6]. The feedback controller relies on sunlight intensity monitoring sensors to accurately measure the intensity of sunlight falling on the solar panels. Typically, these sensors are photovoltaic cells or photodiodes. These sensors convert incident light into a measurable electrical signal, which is then processed by the control algorithm.
3. Effect of Hub Height on Wind Speed
This connection can be expressed with the following expression: as height rises, wind flow rises [7].
𝑉2 = 𝑉1 (ℎ2/h1) 𝛼
The variable stands for the coefficient of ground surface friction, and the elements V1 and V2 represent the airflow rates that were measured at the appropriate reference heights, respectively, h1 and h2. The value of friction coefficient α varies according to the surface. In contrast to rocky surfaces, flat terrain has a low value. Table 1 provides the friction coefficient for various terrain classifications and Figure 2 illustrates how friction coefficients affect wind speed at various heights [7]. Figure 3 indicates the flowchart of tracking algorithm [8].
In environments with lower elevation, wind flow rate demonstrates a comparatively gradual and less consistent increase concerning tower height, as demonstrated in Figure 4. The substantial wind speed disparity between 450 m height and near-ground levels underscores the importance of accounting for proportional coefficient when situating a solar tracker on building rooftops or ground level.
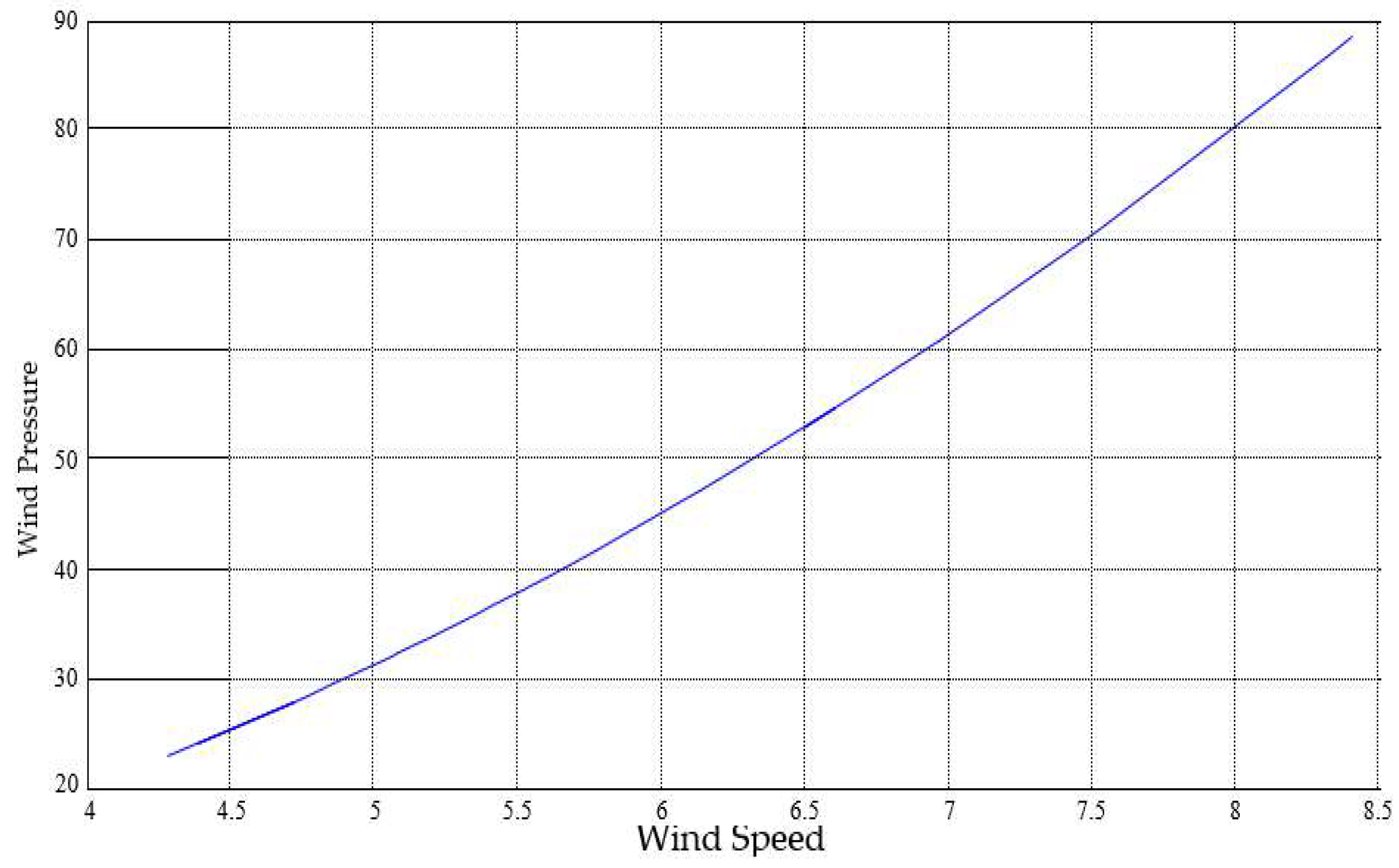
4. Wind Speed vs. Wind Pressure
Wind pressure refers to the effect of wind on a surface area perpendicular to the wind direction. It is caused by the impact of moving air molecules on the surface and can be calculated using the formula [8],
𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 = ½ × (𝑑𝑒𝑛𝑠𝑖𝑡𝑦 𝑜𝑓 𝑎𝑖𝑟) × (𝑤𝑖𝑛𝑑 𝑠𝑝𝑒𝑒𝑑) 2 × (𝑑𝑟𝑎𝑔 𝑐𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡)
The density of air is typically 1.25 kg/m3, whereas the drag coefficient, which is also known as the shape factor, is dimensionless and depends on the shape of the object being acted upon by the wind. For a flat plate, the drag coefficient is equal to 2.0, whereas for a long cylinder, such as an antenna tube, the drag coefficient is approximately 1.2. It is essential to note that the wind speed must be expressed in meters per second (m/s) to obtain the pressure in units of Newtons per square meter (N/m2). Figure 5 displays a plot of wind pressure vs. wind speed.
5. Wind Speed in Jaipur, Rajasthan
When creating a dual-axis STS, wind speed must be taken into account. The wind speed at the site of the system’s installation must be taken into account while constructing a dual-axis STS. The topography, the time of day, and the season are only a few examples of the variables that might affect wind speed. Several sources, including weather stations and internet databases, are available for this data [8].
Once the wind speed has been determined, the system can be set up to operate at its most effective level. It is feasible to design a system that maximises energy production while simultaneously guaranteeing safety and equipment longevity by accounting for the local wind conditions. The experiment was conducted in Jaipur, Rajasthan. Geographical information indicates that it is situated at a longitude of 75.8514° E and a latitude of 26.7751° N. In Jaipur, wind averages approximately 2.6 m/s but can gust up to 9 m/s. Driven by uneven heating and Earth’s rotation, warm air ascends near the equator, whereas surface air moves equatorward. Prevailing winds flow east to west between the equator and latitudes of 30° north and south, leading to often stronger westerly winds in various countries [9].
Table 2 provides information on the wind speed for each month for the preceding five years (2019–2023) in Jaipur, Rajasthan. Solar tracking panels possess the following specifications: They are rated at 335 watts, with a short circuit current of 9.10 amps. At their maximum power point, they operate at an optimal voltage of 37.03 volts and a current of 8.79 amps. Furthermore, they exhibit an open circuit voltage of 45 volts [10].
Figure 6 shows setting a joint mechanical prototype for the created STS. The tracking system’s numerous parts, including the sensors, motors, and framework, are assembled in the prototype. With subfigures displaying the four side views of the construction, the figure provides comprehensive visual insights into the prototype from diverse perspectives. The controller circuit for the proposed dual-axis sun tracking method is depicted in the same Figure 6 [11,12].
This makes it possible to fully understand the physical design of the STS as well as how it would function in use.
Table 3 contains results derived from measurements conducted at two distinct time points. Specifically, measurements taken on 4 May 2023 pertain to a PV system with tracking capabilities, whereas measurements on 18 May 2023 pertain to a stationary PV system. The tabulated data in the table provide a comprehensive repository of measurements encompassing both the stationary and tracking PV systems [13]. This dataset enables a comprehensive evaluation of the efficiency of each system based on the collected data, shedding light on their individual performances [14].
Both systems generate electricity in different ways, which may be caused by variations in the weather or other elements that affect how well the PV systems work. The amount of sunshine determines how much power each system produces [15,16]. The increase in power output throughout the day and the decrease in power production at night serve to amplify this. Table 4 shows the peak power production of the tracking PV system is recorded at 11:30 p.m. with a power output of 180 watts, whereas the maximum power output of the static PV system is recorded at 11:00 a.m. with a power output of 150 watts [17,18].
Figure 7 results depict the varying electricity generation between tracking and static PV systems, with tracking systems generally outperforming static counterparts and the difference expanding as the sun rises higher. In certain instances, tracking systems surpass static ones, particularly in the morning when suboptimal angles may affect tracking PV output [19,20].
6. Conclusions
In summary, this study concentrated on the design and implementation of a hardware-implemented dual-axis solar tracking system with the aim of improving photovoltaic (PV) systems’ energy efficiency. In order to precisely track the current real-time position of the sun, the proposed STS includes both azimuthal and elevation-tracking devices. As a reference input signal, a feedback controller based on sensors continuously measures the brightness of the sun. When the intensity rises over a certain limit, the controller sends a signal to the dual-axis tracking motor to move the PV panel in the direction of the sun. This makes it possible for the PV system to capture the most solar radiation and boost energy effectiveness. The thorough results showed how the STS implemented in hardware increased the productivity of solar PV systems. The system maximises solar energy capture, resulting in increased energy efficiency. It does this by actively tracking the sun’s position in both the east–west (E-W) and north–south (N-S) directions. Overall, the dual-axis solar tracking system’s design and implementation offer a potential response to the drawbacks of fixed flat-plate systems. The results of this study help solar PV systems improve by enabling higher energy efficiency and increased power production.
Author Contributions
All authors have contributed equally to the research and writing of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset used in this research is generated by hardware system and the data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harrison, A.; de Dieu Nguimfack Ndongmo, J.; Alombah, N.H. Robust Nonlinear Control and Maximum Power Point Tracking in PV Solar Energy System under Real Environmental Conditions. Eng. Proc. 2023, 31, 49. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Polo, J.; Ballestrín, J.; Batlles, F.; Portillo, C. Impact of DNI forecasting on CSP tower plant power production. Renew. Energy 2019, 138, 368–377. [Google Scholar] [CrossRef]
- Mahboob, K.; Khan, A.A.; Khan, M.A.; Sarwar, J.; Khan, T.A. Comparison of Li2CO3-Na2CO3-K2CO3, KCl-MgCl2 and NaNO3-KNO3 as heat transfer fluid for different sCO2 and steam power cycles in CSP tower plant under different DNI conditions. Adv. Mech. Eng. 2021, 413, 16878140211011900. [Google Scholar] [CrossRef]
- Ashley, T.; Carrizosa, E.; Fernández-Cara, E. Heliostat field cleaning scheduling for Solar Power Tower plants: A heuristic approach. Appl. Energy 2019, 235, 653–660. [Google Scholar] [CrossRef]
- Bai, Q.; Yang, H.; Cheng, X.; Wang, H. Recombination parameters of the diffusion region and depletion region for crystalline silicon solar cells under different injection levels. Appl. Sci. 2020, 10, 4887. [Google Scholar] [CrossRef]
- Bosman, L.B.; Leon-Salas, W.D.; Hutzel, W.; Soto, E.A. PV system predictive maintenance: Challenges, current approaches, and opportunities. Energies 2020, 16, 1398. [Google Scholar] [CrossRef]
- Altıntaş, M.; Arslan, S. The study of dust removal using electrostatic cleaning system for solar panels. Sustainability 2021, 13, 9454. [Google Scholar] [CrossRef]
- Md, S.; Shakir, D.A.; Fahad, A.A.-S. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar]
- Kishore, T.S.; Singal, S.K. Analysis of Investment Issues and Transmission Schemes for Grid Integration of Remote Renewable Energy Sources. Int. J. Renew. Energy Res. 2015, 5, 483–490. [Google Scholar]
- Lee, D.; Joo, S.-K. Economic Analysis of Large-Scale Renewable Energy (RE) Source Investment Incorporating Power System Transmission Costs. Energies 2023, 16, 7407. [Google Scholar] [CrossRef]
- Fernandes, D.A.; de Almeida, R.G.; Guedes, T.; Filho, A.J.S.; Costa, F.F. State feedback control for DC-photovoltaic systems. Electr. Power Syst. Res. 2017, 143, 794–801. [Google Scholar] [CrossRef]
- Li, X.; Wen, H.; Hu, Y.; Du, Y.; Yang, Y. A Comparative Study on Photovoltaic MPPT Algorithms Under EN50530 Dynamic Test Procedure. IEEE Trans. Power Electron. 2021, 36, 4153–4168. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Wen, H.; Xiao, W. Comprehensive Studies on Operational Principles for Maximum Power Point Tracking in Photovoltaic Systems. IEEE Access 2019, 7, 121407–121420. [Google Scholar] [CrossRef]
- Kjaer, S.B. Evaluation of the “Hill Climbing” and the “Incremental Conductance” Maximum Power Point Trackers for Photovoltaic Power Systems. IEEE Trans. Energy Convers. 2012, 27, 922–929. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. A Fast Current-Based MPPT Technique Employing Sliding Mode Control. IEEE Trans. Ind. Electron. 2013, 60, 1168–1178. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Framework of Maximum Power Extraction from Solar PV Panel Using Self Predictive Perturb and Observe Algorithm. IEEE Trans. Sustain. Energy 2018, 9, 895–903. [Google Scholar] [CrossRef]
- Abdelsalam, A.; Massoud, A.; Ahmed, S.; Enjeti, P. High-Performance Adaptive Perturb and Observe MPPT Technique for Photovoltaic-Based Microgrids. IEEE Trans. Power Electron. 2011, 26, 1010–1021. [Google Scholar] [CrossRef]
- Xiao, W.; Dunford, W.G. A modified adaptive hill climbing MPPT method for photovoltaic power systems. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 3, pp. 1957–1963. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A Variable Step Size INC MPPT Method for PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
Figure 1.
Angle of incident light upon the solar cell.
Figure 2.
Closed loop solar tracker PV system.
Figure 3.
Flowchart of tracking algorithm.
Figure 4.
Influence of fractional coefficients on wind speed (α = 0.2, 0.3, and 0.4).
Figure 5.
Wind pressure vs. wind speed (m/s).
Figure 6.
Hardware structure of DASTS.
Figure 7.
Power generated by the tracking solar array and the static solar array.
Table 1.
Value of friction coefficients (α) of various terrains.
| Terrain Type | Friction Coefficients |
|---|---|
| Lake, ocean | 0.100 |
| High grass-level ground | 0.150 |
| Smooth terrain and hard ground | 0.100 |
| Heavily forested region | 0.250 |
| Tall crops, hedges, and shrubs | 0.200 |
| Tall structures in the city | 0.400 |
| The little community has several bushes and trees | 0.300 |
Table 2.
Last 5 years wind speed (m/s) data in Jaipur, Rajasthan.
| Month | Year_2019 | Year_2020 | Year_2021 | Year_2022 | Year_2023 | Averages |
|---|---|---|---|---|---|---|
| January | 5.8 | 6.8 | 5.7 | 6.5 | 6.8 | 7.3 |
| February | 8.2 | 7.8 | 6.3 | 8 | 6.4 | 7.3 |
| March | 8.2 | 9.3 | 8.5 | 7.7 | 8 | 8.3 |
| April | 8.6 | 9.4 | 7.2 | 8.3 | 8 | 8.3 |
| May | 8.7 | 11.2 | 9.8 | 12.4 | 8.0 | 10.5 |
| June | 9.9 | 10.8 | 11.9 | 12.2 | 8.5 | 10.2 |
| July | 10.8 | 9.3 | 11.8 | 8.8 | **** | 10.3 |
| August | 8.5 | 4.7 | 11.2 | 9.7 | **** | 8.8 |
| September | 7.5 | 4.2 | 9.9 | 9 | **** | 7.7 |
| October | 4.5 | 3.4 | 6.3 | 6.4 | **** | 5.1 |
| November | 6.9 | 5.1 | 4.4 | 4.5 | **** | 5.2 |
| December | 5 | 2.3 | 5.8 | 5 | **** | 4.6 |
**** denotes the data not available for this month.
Table 3.
Performance evaluation of fixed and tracking PV system.
| Time | PV Tracking System | PV Static System | ||||
|---|---|---|---|---|---|---|
| Current (A) | Voltage (V) | Power (Watt) | Current (A) | Voltage (V) | Power (Watt) | |
| 08:00 | 5 | 14 | 60 | 3.5 | 11 | 38.5 |
| 08:30 | 4.5 | 18 | 81 | 4 | 11 | 44 |
| 09:00 | 5.5 | 20 | 110 | 5.8 | 17 | 98.6 |
| 09:30 | 7.5 | 20 | 150 | 6.5 | 19 | 123.5 |
| 10:00 | 7.5 | 20 | 150 | 7.2 | 18 | 129.6 |
| 10:30 | 7.8 | 20 | 156 | 7.2 | 18 | 129.6 |
| 11:00 | 7 | 20 | 140 | 7.5 | 20 | 150 |
| 11:30 | 9 | 20 | 180 | 7.5 | 20 | 150 |
| 12:00 | 8 | 21 | 168 | 7.8 | 20 | 156 |
| 12:30 | 8.2 | 20 | 164 | 7.3 | 21 | 153.3 |
| 01:00 | 8 | 20 | 160 | 6.8 | 21 | 142.8 |
| 01:30 | 7 | 20 | 140 | 6.2 | 20 | 124 |
| 02:00 | 6.5 | 20 | 130 | 6 | 20 | 120 |
| 02:30 | 6.2 | 18 | 111.6 | 5 | 20 | 100 |
| 03:00 | 5 | 15 | 75 | 2.5 | 10 | 25 |
| 03:30 | 3.5 | 15 | 52.5 | 2.5 | 10 | 25 |
| 04:00 | 3.0 | 10 | 30 | 1.5 | 10 | 15 |
Table 4.
A study comparing the amount of electricity produced by tracking and stationary solar power systems [17,18].
| Time | Power of Tracking PV System (Watt) | Power of Static PV System (Watt) |
|---|---|---|
| 08:00 | 60 | 38.5 |
| 08:30 | 81 | 44 |
| 09:00 | 110 | 98.6 |
| 09:30 | 150 | 123.5 |
| 10:00 | 150 | 129.6 |
| 10:30 | 156 | 129.6 |
| 11:00 | 140 | 150 |
| 11:30 | 180 | 150 |
| 12:00 | 168 | 156 |
| 12:30 | 164 | 153.3 |
| 01:00 | 160 | 142.8 |
| 01:30 | 140 | 124 |
| 02:00 | 130 | 120 |
| 02:30 | 111.6 | 100 |
| 03:00 | 75 | 25 |
| 03:30 | 52.5 | 25 |
| 04:00 | 30 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Mamodiya, U.; Tiwari, N. Design and Implementation of Hardware-Implemented Dual-Axis Solar Tracking System for Enhanced Energy Efficiency. Eng. Proc. 2023, 59, 122. https://doi.org/10.3390/engproc2023059122
AMA Style
Mamodiya U, Tiwari N. Design and Implementation of Hardware-Implemented Dual-Axis Solar Tracking System for Enhanced Energy Efficiency. Engineering Proceedings. 2023; 59(1):122. https://doi.org/10.3390/engproc2023059122
Chicago/Turabian StyleMamodiya, Udit, and Neeraj Tiwari. 2023. "Design and Implementation of Hardware-Implemented Dual-Axis Solar Tracking System for Enhanced Energy Efficiency" Engineering Proceedings 59, no. 1: 122. https://doi.org/10.3390/engproc2023059122
