Abstract
Green Ports have emerged due to the increase in air pollution from emissions generated by maritime traffic and the dispersion of particles, as well as water pollution from spills. The primary objective of this study is to anticipate episodes of atmospheric pollution related to cargo-handling activities and assess the quantitative causality between these variables. We employ a causality inference based on time series analysis to investigate the applicability and validity of these techniques in a real-world problem setting. Specifically, methods such as the Granger Test and PCMCI are evaluated and compared with these data. The results demonstrate that cargo handling at the port under study has some causal influence on the PM (particulate matter) measurements. Finally, the PCMCI method is proposed as the most robust among the algorithms considered in this study.
1. Introduction
The growth of commercial activities and the need for competitiveness in the global market are forcing ports around the world to evaluate all possibilities systematically and continuously for optimization and the reduction of related costs and externalities. Among the main adverse effects between port activity and the environment, air pollution (due to emissions from maritime traffic or the dispersion of particles) and water pollution (spills) stand out.
Atmospheric pollutants are emitted from ports through various sources and are both directly and indirectly associated with port activities. The coexistence of multiple transportation modes, including vessels, bulk cargo, handling equipment, and rail locomotives, collectively contributes to emissions of particulate matter (PM) and greenhouse gases linked to maritime operations [1].
These problems have led to the emergence of a new port paradigm: the Green Port, in which sustainability (in its three aspects: social, economic and environmental) is the central pillar. The Green Port concept introduces these three aspects in the development and operation of ports in order to find a balance between them, resulting in ports that are competitive and integrated with both the city that hosts them and the environment [2].
This text describes the implementation of a study aimed at predicting when an episode of airborne particle pollution may occur due to port activities related to the loading and unloading of bulk cargo. To achieve this, two different methodologies are employed: firstly, a simpler method like the Granger test, and secondly, a more sophisticated method like PCMCI. These studies are applied to real data obtained from bulk cargo activities in four specific areas of the Castellò Port along with data on pollutants collected from five different stations located within the port.
2. Materials and Methods
2.1. The Study Site, Castellò Port
The present study focuses on five air quality monitoring stations in the Castellò Port (Tramontana, Gregal, Levante, Poniente and Siroco) and the four docks in color (CS06 in red, CS26 in yellow, CS05 in green and CS09 in blue). These zones are reflected in the figure below (Figure 1).
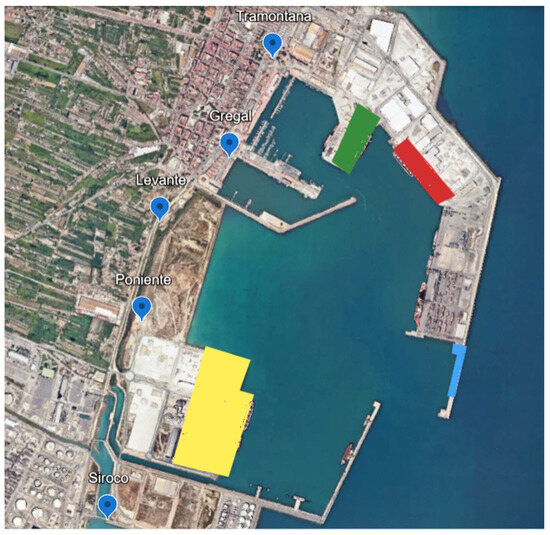
Figure 1.
Study site located at Castellò Port (Castellón, Spain).
2.2. The Data Understanding
Data were acquired by Port Authority of Castellò (PAC). As the raw data are very heterogeneous, considerable work has been carried out to transform them into versions suitable for further processing. As the useful port operations data only covered the years 2020 and 2021, these two years were chosen for both datasets, comprising air quality parameters and port operations.
2.2.1. Air Quality
Since not all the stations have the same sensors and therefore do not measure the same variables, the parameters that are common to all have been selected. Regarding the pre-processing of the data, only one datum in the time series of the maximum wind speed for the year 2021 at the Poniente station was replaced by the average value of the immediate neighbors, as it was clearly an outlier. Therefore, we can say that these time series are clearly very good in terms of data quality.
Finally, the final air quality data consists of 5 multidimensional time series, each associated with a monitoring station and where the dimensions correspond to the following variables for 2020 and 2021: [μg/m3], [μg/m3], wind direction [º], hourly mean wind speed [m/s] and maximum hourly wind speed [m/s].
Given the inherent cleanliness of these time series, it was not considered necessary to perform any pre-processing beyond reformatting the data or grouping them in a more convenient way for the study.
2.2.2. Port Operations
The port operations data required much more pre-processing than the air quality data. The data itself did not consist of a time series as such, but of a series of records of ship arrivals and departures at the docks, where the following parameters were monitored: tons unloaded, dock, type of goods, vessel, hands, date of arrival and departure, among others. The period covered is from 2019 to 2021, with data received with a time resolution of 6 h.
2.3. Causal Analysis Techniques
Inferring causality is a remarkably important problem because, unlike descriptive statistical analysis, it allows decisions to be made in a rational and justified way. However, there is no universal definition of causality, although several attempts have been made [3]. The first quantitative notion of causality came from N. Wiener in 1956, in the context of the study of temporal signals. Later, Clive W.J. Granger implemented and popularized this formulation (called Granger causality in his honor), which even won him the Nobel Prize in Economics in 2003 and it is the first family of methods to be studied in this paper (Section 2.2.1). However, it is a method that, as will be seen below, is limited to linear relationships between time series. It did not take long, therefore, for a large number of generalizations (and other approaches) of the same method to appear, taking into account non-linearity, both from the point of view of econometrics and from that of physics and non-linear dynamical systems [4]. On the other hand, concepts from information theory, first introduced by Schreiber in terms of transfer entropy [5], have been used to infer causality, notably in the work of Palus [6], such as conditional mutual information. In addition, other types of causality and inference methods have appeared; one can read about current causality techniques in [7,8]. The methods selected for investigation in this paper draw on several of these concepts. In particular, following an overview of different methods, this paper presents two methods that correspond to two different but related approaches, which are described in detail in the following sections.
2.3.1. Granger Causality
Granger’s method assesses causality in that the addition of a variable as a component of the predictive model, the target variable, increases the predictive power of the model. Intuitively, this means that, in Granger’s sense, a process X causes a process Y if predictions about future values of Y are more accurate when information from X’s past is considered. More specifically, we want to test the null hypothesis of the process “X does not (Granger) cause Y”. To this end, both VAR(T) (Vector Auto Regressive) model with and without the functional dependence of X are considered (1) and (2):
where , and are the coefficients of the model and ϵ is a component characterizing the signal noise, while T is the order of the model, i.e., the maximum time delay considered. In this model, the process X is assumed to influence Y if the coefficients are not null.
where the coefficients of the model are the same as in the previous case.
Thus, the following (null) hypotheses are to be tested:
in comparison with the alternative scenarios:
Then, after adjusting the coefficients (e.g., by least squares) of both models, a statistical test of significance, such as Fisher’s F-test, is applied (which compares the variance of the residuals of the model including only Y with that of the model including both X and Y):
where and are the sum of the squared residuals of the restricted and unrestricted model, respectively (Equations (1) and (2)), q is the number of null coefficients and p is the number of observations. Thus, depending on the value of F, the null hypothesis can be rejected (or not) and X can be considered to cause Y (or not) in the Granger sense.
Before applying the Granger test, it is necessary to check that the stationarity condition of the time series in question is satisfied, in order to construct time series models that assume this property. To do this, Augmented Dickey–Fuller (ADF) and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests are evaluated.
2.3.2. PCMCI
This method of causal inference between time series, proposed by Runge in [8], is based on the concept of conditional independence to estimate the strength and directionality of causal relationships between highly interdependent multivariate time series. This comes from PC (Park and Clark) and MCI (Momentary Conditional Independence) methods. Let us consider a dynamic system (therefore, multivariable, where the index t indicates the time instant and the upper index distinguishes the different variables that compose it) in which the following is true:
where is a possible nonlinear functional dependence, is a mutually independent dynamic, noise, and denotes the “causal parents” of the variable in the entire history of the variables; thus, a causal link exists if , where is a time delay. The PCMCI algorithm then attempts to find the causal parent of different time series with different time lags (). For this purpose, and as already indicated, this method presents two different stages [8]:
- Identification of some relevant initial relatedness conditions for all time series by means of a PC algorithm (Markov discovery type). After this step, an approximation of the true parent distribution is obtained, possibly including false positives.
- Refinement of the identification of (control of false positives) by means of a Momentary Conditional Independence MCI analysis.
3. Results
The results can be seen in Figure 2 and Figure 3, where they have been classified according to the operating dock. Gregal, Poniente and Siroco stations were chosen among all the stations for comparisons between them, being the ones that are more relevant.
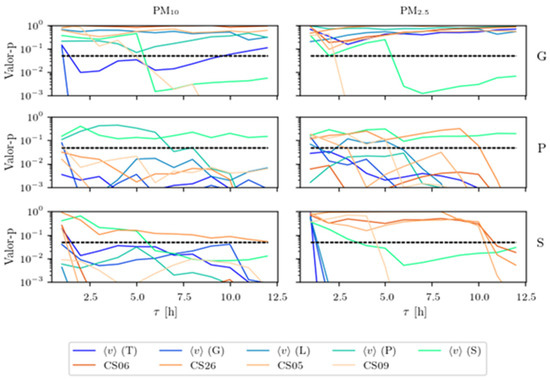
Figure 2.
Granger causality between the variables of average speed and tons per hour discharged at the four docks (by color, indicated in the legend, and the variables of granulated material in suspension y ).
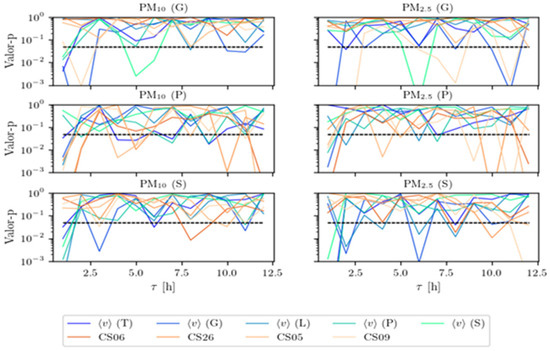
Figure 3.
p-values according to the PCMCI algorithm for the different cause and effect variables. The statistical significance value of 0.05 is indicated by the dashed line.
3.1. Granger
In particular, the docks are identified by their initials (G: Gregal; P: Poniente; S: Siroco) in the rows, and the causal relationships from the variables indicated in the legend to the and variables (in the columns) are shown. Recall that the Granger test indicates causality in cases where the p-value is less than 0.05.
For both docks, the p-value curves as a function of the delay time τ have a decreasing shape, with few instances of causality for delays of 1 h. The wind speed at Siroco stands out as the variable that, on average, has the least causal effect (in the Granger sense) on the others. Similarly, the variables representing tons discharged discharged per hour show mixed results, with slightly more causal relationships appearing towards the variable than towards the variable.
In Figure 2, in short, there are many causal relationships that can be complex to identify among so many variables. In addition, the high number of causal detections is remarkable, even though there are some monitoring stations (Gregal) that show practically no causality for the tons of bulk discharged. A priori, the parameter that is most causally influenced by bulk discharge is (P), followed by (S).
3.2. PCMCI
Following the same methodology as in the previous cases, it was applied to all possible pairs of cause and target variables defined above, for a maximum time lag of 12 h. P-values below a statistical significance level of 0.05 are considered to indicate a causal relationship.
4. Conclusions
When investigating causality in relation to air quality in port areas, air quality can influence the concentration of particulate matter and thus the quality of the surrounding air. Two common approaches to address this relationship are Granger analysis and the use of the Multivariate Principal Component Method (PCMCI). Regarding the causal inference algorithms, a considerable variability of results is found among all the methods. According to the Granger method, wind has a causal strength on the PM variables (in general, stronger relationships seem to be observed for the same station where it is measured). Similarly, the bulk series of the CS06, CS05 and CS09 docks stand out as influencing the PM measurements, especially at the Siroco and Poniente stations.
According to the PCMCI algorithm, which is in principle more robust than the others, the bulk discharges of CS05 and CS09 stand out as the most important variables causing the PM dynamics at the Poniente and Gregal stations (for PM2.5), respectively. However, these are not the closest stations to each of these terminals, which could be related to the prevailing winds.
On the other hand, data collection in ports could lead to issues related to Big Data in terms of volume data, variety data and velocity of data acquisition. The solutions proposed in the paper (Granger and PCMCI) can address Big Data issues to some extent, but their capabilities may vary, depending on the type of the analysis.
In conclusion, the choice between Granger and PCMCI for the causality analysis of air quality in ports such as Castellò Port depends on the complexity of the relationships to be investigated. PCMCI offers a significant advantage in allowing the detection of causal relationships beyond linear ones, which may lead to a complete understanding.
Author Contributions
Conceptualization and methodology, R.M., J.C.S.-G. and I.F.; data curation, E.M. and J.C.S.-G.; formal analysis, E.M., J.C.S.-G. and R.M.; validation, R.M. and I.F., writing—original draft preparation, J.C.S.-G. and R.M.; writing—review and editing I.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Instituto de Fomento de la Región de Murcia (INFO) under the Program of grants aimed at Technological Centers of the Region of Murcia for the realization of non-economic R&D activities. Modality 1: Independent R&D Projects, with File No.: 2021.08.CT01.000044.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are not publicly available due to privacy reasons.
Acknowledgments
We thank Castellò Port for providing us with the necessary information and relevant data to carry out this study, especially to Inés Lopez, Maria José Rubio and Bernat Ibañez.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chang, C.C.; Wang, C.M. Evaluating the effects of green port policy: Case study of Kaohsiung harbor in Taiwan. Transp. Res. Part D Transp. Environ. 2012, 17, 185–189. [Google Scholar] [CrossRef]
- Davarzani, H.; Fahimnia, B.; Bell, M.; Sarkis, J. Greening ports and maritime logistics: A review. Transp. Res. Part D Transpor Environ. 2016, 48, 473–487. [Google Scholar] [CrossRef]
- Hlaváčková-Schindler, K.; Paluš, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Hiemstra, C.; Jones, J.D. Testing for Linear and Nonlinear Granger Causality in the Stock Price-Volume Relation. J. Financ. 1994, 49, 1639–1664. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Palus, M.; Hoyer, D. Detecting nonlinearity and phase synchronization with surrogate data. IEEE Eng. Med. Biol. Mag. 1998, 17, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Eichler, M. Causal inference with multiple time series: Principles and problems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110613. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Bathiany, S.; Bollt, E.; Camps-Valls, G.; Coumou, D.; Deyle, E.; Glymour, C.; Kretschmer, M.; Mahecha, M.D.; Muñoz-Marí, J.; et al. Inferring causation from time series in Earth system sciences. Jakob Zscheischler 2019, 10, 19. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).