The Effect of Fear on a Diseased Prey–Predator Model with Predator Harvesting †
Abstract
:1. Introduction
2. Model Formation
3. The Presence of Equilibrium Points
- The trivial equilibrium point .
- The diseased prey-free and predator-free equilibrium point .
- The predator-free equilibrium point ,where.
- The infection-free equilibrium point , where, and .
- The interior equilibrium point ,where ,,and is the unique positive root of the quadratic equation ,with , , .
4. Analyses of Local Stability
5. Hopf Bifurcation Analysis
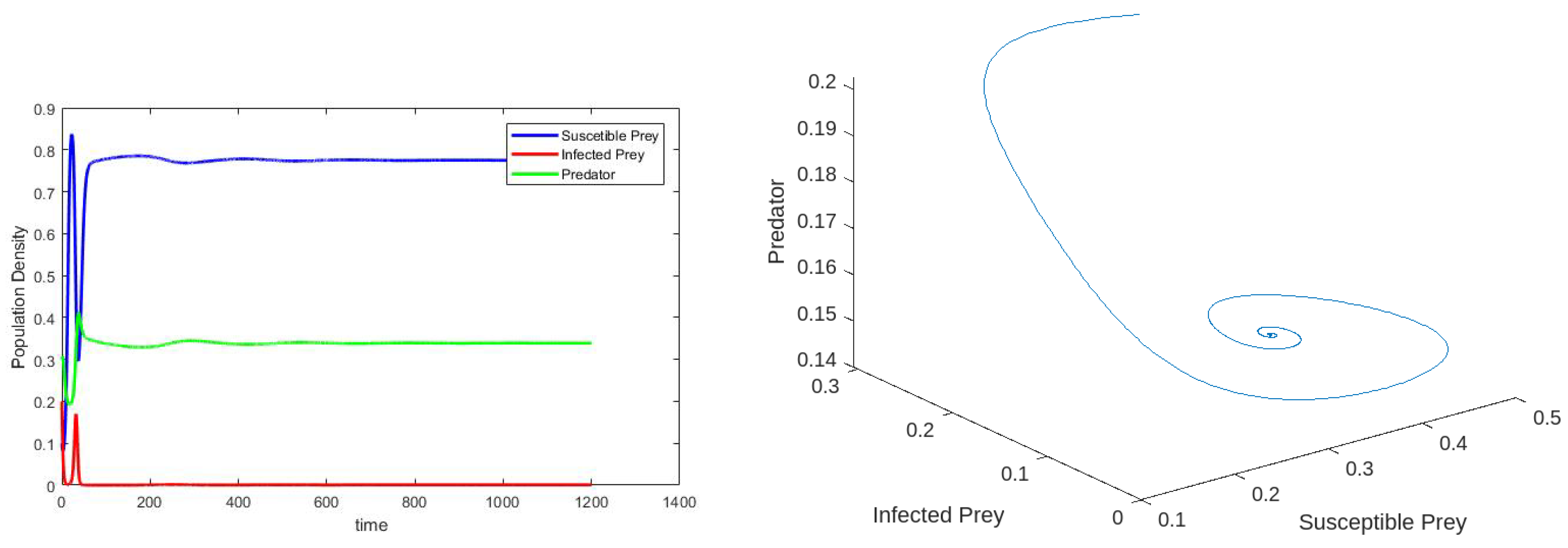
6. Numerical Simulations
Effect of Varying the Harvesting Rate h
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashwin, A.; Sivabalan, M.; Divya, A.; Siva Pradeep, M. Dynamics of Holling Type II Eco-Epidemiological Model with Fear Effect, Prey Refuge, and Prey Harvesting. Available online: https://sciforum.net/paper/view/14404 (accessed on 25 October 2023).
- Divya, A.; Sivabalan, M.; Ashwin, A.; Siva Pradeep, M. Dynamics of Ratio Dependent Eco Epidemiological Model with Prey Refuge and Prey Harvesting. Available online: https://sciforum.net/paper/view/14744 (accessed on 25 October 2023).
- Yue, Q. Dynamics of a modified Leslie-Gower predator-prey model with Holling-type II schemes and a prey refuge. Springerplus 2016, 5, 461. [Google Scholar] [CrossRef] [PubMed]
- Lavanya, R.; Vinoth, S.; Sathiyanathan, K.; Tabekoueng, Z.N.; Hammachukiattikul, P.; Vadivel, R. Dynamical Behavior of a Delayed Holling Type-II Predator-Prey Model with Predator Cannibalism. J. Math. 2022, 2022, 4071375. [Google Scholar] [CrossRef]
- Melese, D.; Muhye, O.; Sahu, S.K. Dynamical behavior of an eco-epidemiological model incorporating prey refuge and prey harvesting. Appl. Appl. Math. Int. J. (AAM) 2020, 15, 1193–1212. [Google Scholar]
- Tripathi, J.P.; Jana, D.; Tiwari, V. A Beddington–DeAngelis type one-predator two-prey competitive system with help. Nonlinear Dyn. 2018, 94, 553–573. [Google Scholar] [CrossRef]
- Tripathi, J.P.; Abbas, S.; Thakur, M. A density dependent delayed predator–prey model with Beddington–DeAngelis type function response incorporating a prey refuge. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 427–450. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Vadivel, R.; Zhai, G.; Vinoth, S. Finite-time stability analysis and control of stochastic SIR epidemic model: A study of COVID-19. Biomed. Signal Process. Control. 2023, 86, 105123. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Biological Meaning |
|---|---|
| X | Susceptible Prey |
| Y | Infected Prey |
| Z | Predator |
| r | The intrinsic growth rate of prey |
| K | The carrying capacity of the environment |
| The half-saturation constant | |
| Predation rate of susceptible prey | |
| Predation rate of infected prey | |
| c | Conversion coefficient from the prey to predator |
| The death rate of infected prey | |
| The death rate of predator population | |
| The infection rate | |
| H | The catchability coefficient of the predator |
| E | Harvesting effort |
| Parameters | Indicative Number |
|---|---|
| Variable | |
| Variable | |
| h | 0.1 |
| a | 0.2 |
| d | 0.6 |
| r | 0.3 |
| 0.4 | |
| c | 0.5 |
| 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natesan, R.; Shanmugam, M.; Manickasundaram, S.P.; Nallasamy Prabhumani, D. The Effect of Fear on a Diseased Prey–Predator Model with Predator Harvesting. Eng. Proc. 2023, 56, 124. https://doi.org/10.3390/ASEC2023-15248
Natesan R, Shanmugam M, Manickasundaram SP, Nallasamy Prabhumani D. The Effect of Fear on a Diseased Prey–Predator Model with Predator Harvesting. Engineering Proceedings. 2023; 56(1):124. https://doi.org/10.3390/ASEC2023-15248
Chicago/Turabian StyleNatesan, Raja, Muthukumar Shanmugam, Siva Pradeep Manickasundaram, and Deepak Nallasamy Prabhumani. 2023. "The Effect of Fear on a Diseased Prey–Predator Model with Predator Harvesting" Engineering Proceedings 56, no. 1: 124. https://doi.org/10.3390/ASEC2023-15248
APA StyleNatesan, R., Shanmugam, M., Manickasundaram, S. P., & Nallasamy Prabhumani, D. (2023). The Effect of Fear on a Diseased Prey–Predator Model with Predator Harvesting. Engineering Proceedings, 56(1), 124. https://doi.org/10.3390/ASEC2023-15248






