On the Quantification of the GNSS Signals’ Quality for RFI Assessment †
Abstract
:1. Introduction
2. Statistical Characteristics of Data Distribution
2.1. Skewness
- If the skewness is between −0.5 and 0.5, the data are nearly symmetrically distributed around the mean.
- If the skewness is between −1 and −0.5 (negative skewed) or between 0.5 and 1 (positive skewed), the sample data are representative of a slightly skewed distribution.
- If the skewness is lower than −1 (negative skewed) or greater than 1 (positive skewed), the sample data would represent an extremely skewed distribution.
2.2. Kurtosis
3. Distribution Analysis for RFI Assessment Techniques
Mathematical Formulation of the Shapiro–Wilk Test
4. Experimental Setup
5. Results and Discussion
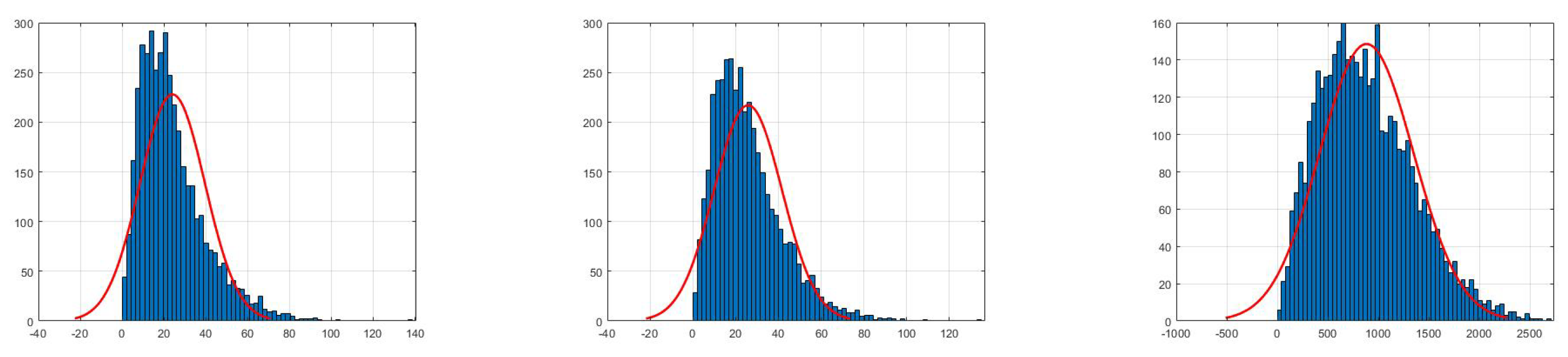
5.1. Effect of Noise on the Statistical Properties
5.2. Shapiro–Wilk Test Results
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Coast Guard Navigation Center. GPS Navigation Problems. Available online: https://www.navcen.uscg.gov/?pageName=GPSProblems (accessed on 20 March 2023).
- Nandra, R.; Sridevan, S.; Hancke, R. GPS Spoofing: The Next Generation. IEEE Commun. Mag. 2018, 56, 180–186. [Google Scholar]
- Humphreys, T.E.; Ledvina, B.M. Assessing the Spoofing Threat: Development of a Portable GPS Civilian Spoofer. J. Field Robot. 2013, 30, 531–548. [Google Scholar]
- Dovis, F. GNSS Interference Threats and Countermeasures; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Thompson, R.J.; Wu, J.; Balaei, A.T.; Dempster, A.G. Detection of RF interference to GPS using day-to-day C/N0 differences. In Proceedings of the International Symposium on GNSS, Taipei, Taiwan, 26–28 October 2010. [Google Scholar]
- Sun, K.; Zhang, T. A New GNSS Interference Detection Method Based on Rearranged Wavelet–Hough Transform. Sensors 2021, 21, 1714. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Jin, T.; Yang, D. An Improved Time-Frequency Analysis Method in Interference Detection for GNSS Receivers. Sensors 2015, 15, 9404–9426. [Google Scholar] [CrossRef] [PubMed]
- Balaei, A.T.; Dempster, A.G. A statistical inference technique for GPS interference detection. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1499–1511. [Google Scholar] [CrossRef]
- Motella, B.; Pini, M.; Presti, L.L. GNSS interference detector based on Chi-square Goodness-of-fit test. In Proceedings of the 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) and European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Specht, M. Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size. Sensors 2020, 20, 7144. [Google Scholar] [CrossRef] [PubMed]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Smirnov, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Francia, R. An Approximate Analysis of Variance Test for Normality. J. Am. Stat. Assoc. 1972, 67, 215–216. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Ahmad, F.; Khan, R.A. A power comparison of various normality tests. Pak. J. Stat. Oper. Res. 2015, 11, 331–345. [Google Scholar] [CrossRef]
- RTL-SDR. Available online: https://www.rtl-sdr.com/about-rtl-sdr/ (accessed on 20 March 2023).


| Parameter | Value |
|---|---|
| Tune Low (MHz) | 24 |
| Tune Max (MHz) | 1766 |
| RX Bandwidth (MHz) | 3.2/2.56 (Stable) |
| ADC Resolution (Bits) | 8 |
| ADC Sampling Frequency (MHz) | 2.048 |
| Intermediate Frequency (Hz) | 0 |
| GNSS Signal and Noise | Sample Size | Skewness | Kurtosis |
|---|---|---|---|
| L1 with no noise | 1024 | 1.43 | 5.66 |
| L1 with white noise @ −20 dB | 1024 | 1.30 | 5.29 |
| L1 with white noise @ −40 dB | 1024 | 0.56 | 3.25 |
| L1 with white noise @ −60 dB | 1024 | 0.72 | 3.48 |
| L1 with white noise @ −80 dB | 1024 | 0.58 | 3.00 |
| L1 with no noise | 2048 | 1.52 | 6.67 |
| L1 with white noise @ −20 dB | 2048 | 1.39 | 6.15 |
| L1 with white noise @ −40 dB | 2048 | 0.67 | 3.25 |
| L1 with white noise @ −60 dB | 2048 | 0.61 | 3.27 |
| L1 with white noise @ −80 dB | 2048 | 0.6 | 3.00 |
| L1 with no noise | 4096 | 1.26 | 5.17 |
| L1 with white noise @ −20 dB | 4096 | 1.16 | 4.96 |
| L1 with white noise @ −40 dB | 4096 | 0.62 | 3.21 |
| L1 with white noise @ −60 dB | 4096 | 0.60 | 3.11 |
| L1 with white noise @ −80 dB | 4096 | 0.70 | 3.48 |
| L1 with no noise | 8192 | 1.39 | 6.00 |
| L1 with white noise @ −20 dB | 8192 | 1.25 | 5.52 |
| L1 with white noise @ −40 dB | 8192 | 0.62 | 3.14 |
| L1 with white noise @ −60 dB | 8192 | 0.62 | 3.26 |
| L1 with white noise @ −80 dB | 8192 | 0.66 | 3.32 |
| GNSS Signal | Sample Size | Test Statistics Value (w) | p-Value | SK-Test Inference |
|---|---|---|---|---|
| L1 with white noise @ −20 dB | 1024 | 0.04 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −40 dB | 1024 | 0.004 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −60 dB | 1024 | 4.4 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −80 dB | 1024 | 4.4 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −20 dB | 2048 | 0.09 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −40 dB | 2048 | 0.009 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −60 dB | 2048 | 8.8 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −80 dB | 2048 | 8.5 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −20 dB | 4096 | 0.13 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −40 dB | 4096 | 0.016 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −60 dB | 4096 | 1.79 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −80 dB | 4096 | 1.78 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −20 dB | 8192 | 0.32 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −40 dB | 8192 | 0.03 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −60 dB | 8192 | 3.48 × 10 | 1 | Null Hypothesis not rejected |
| L1 with white noise @ −80 dB | 8192 | 3.5 × 10 | 1 | Null Hypothesis not rejected |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, N. On the Quantification of the GNSS Signals’ Quality for RFI Assessment. Eng. Proc. 2023, 54, 19. https://doi.org/10.3390/ENC2023-15440
Ahmed N. On the Quantification of the GNSS Signals’ Quality for RFI Assessment. Engineering Proceedings. 2023; 54(1):19. https://doi.org/10.3390/ENC2023-15440
Chicago/Turabian StyleAhmed, Naveed. 2023. "On the Quantification of the GNSS Signals’ Quality for RFI Assessment" Engineering Proceedings 54, no. 1: 19. https://doi.org/10.3390/ENC2023-15440
APA StyleAhmed, N. (2023). On the Quantification of the GNSS Signals’ Quality for RFI Assessment. Engineering Proceedings, 54(1), 19. https://doi.org/10.3390/ENC2023-15440






