Anomaly and Fraud Detection in Credit Card Transactions Using the ARIMA Model †
Abstract
:1. Introduction
2. Fraud Detection with Time Series Approach
2.1. ARIMA Model with Time Series Analysis
- Autoregressive ModelThe AR(p) model is defined by the equation below; it assumes that there is a dependent linear relation between the observation and the values of a specified number of lagged (previous) observations plus an error term.where are the coefficients of the model, p is a non-negative integer, c is a constant and .
- Moving Average ModelThe MA(p) model is defined by the equation below; it makes use of the dependency between an observation and the residual errors resulting from the application of a moving average model to lagged observations.where is the mean of the series, are the coefficients of the model, and q is the order and .
2.2. Estimation Process of ARIMA
- 1.
- Identification, which refers to the use of all available data and related information to select the model that best represents the time series. This phase should, however, be split into two sub-steps:
- (a)
- DifferencingThe first step requires the establishment of whether the time series is stationary or not in order to determine whether it requires differencing. The augmented Dickey–Fuller (ADF) test is a technique that can be used to verify if the time series on hand is stationary. The null hypothesis of the ADF test states that the time series can be represented by a unit root, meaning it presents a time-dependent structure and that it is, thus, not stationary; consequently, rejecting the null hypothesis implies that the time series is stationary.
- (b)
- Configuration of p and qDuring this phase, it is helpful to use the correlogram to visualise the autocorrelation function (ACF) and the partial autocorrelation function (PACF) that can help to determine a suitable choice for the orders p and q. The fundamental difference between the two functions is that the PACF removes the linear dependence between the intermediate variables in order to return only the correlation between the present and lagged value. Briefly, whereas the autocorrelation function of AR(p) tails off, its partial autocorrelation function cuts off after the lag p. Conversely, the autocorrelation function of MA(q) has a cut-off after the lag q, while its partial autocorrelation function tails off.
- 2.
- Estimation, which refers to the training phase. Once the values of p, d, q have been established, the and coefficients can be estimated. This method uses the maximum likelihood estimation process, which is solved by non-linear function maximisation; for more details about this phase, the reader is referred to [11,12].
- 3.
- Diagnostics, which refers to the evaluation of the model and identification of improvements. This step involves the determination of issues in the model to verify whether it is able to effectively summarise the underlying data. The forecast residuals provide an important source of information for diagnostics. In an ideal model, the error will resemble white noise and will be normally distributed with a mean of 0 and a constant variance. In addition to this, an ideal model would also leave no temporal structure in the residuals, as they should have been learned.
2.3. Fraud Detection with ARIMA Model on Daily Counts of Transactions
- 1.
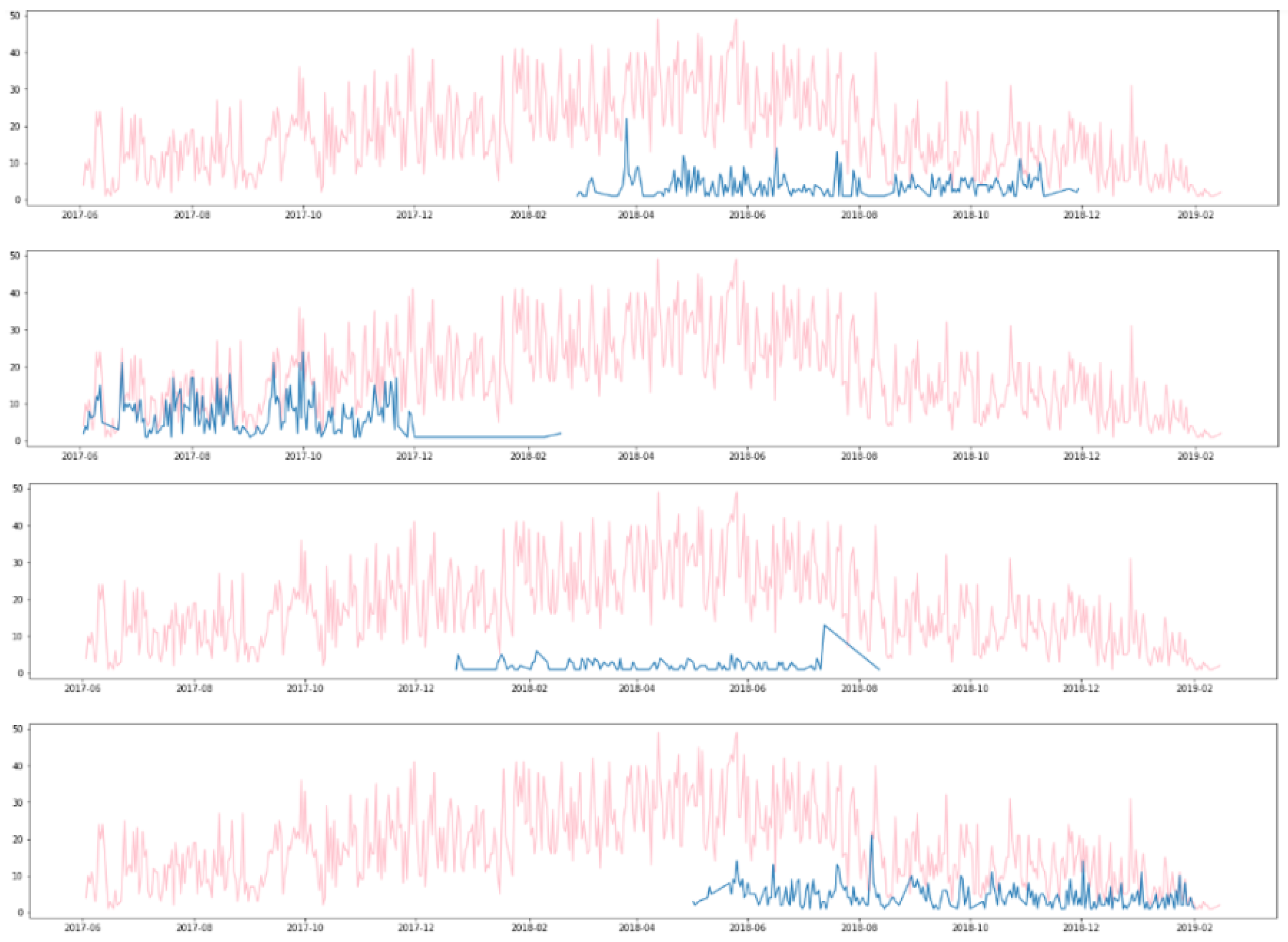
- The time series is split into training and testing set; it is important that the training set only contains legitimate transactions so that the model can learn the legitimate behaviour of the customers. This should then allow for the identification of anomalies.
- 2.
- In the training set, based on the legitimate transactions, the order of the ARIMA model is identified using the Box–Jenkins method, and, then, the parameters of ARIMA are estimated. During this phase, care is taken to ensure that the estimated coefficients are significant and that there is no temporal structure left in the residuals. Finally, in the testing set, one-step ahead prediction is performed using rolling windows.
- 3.
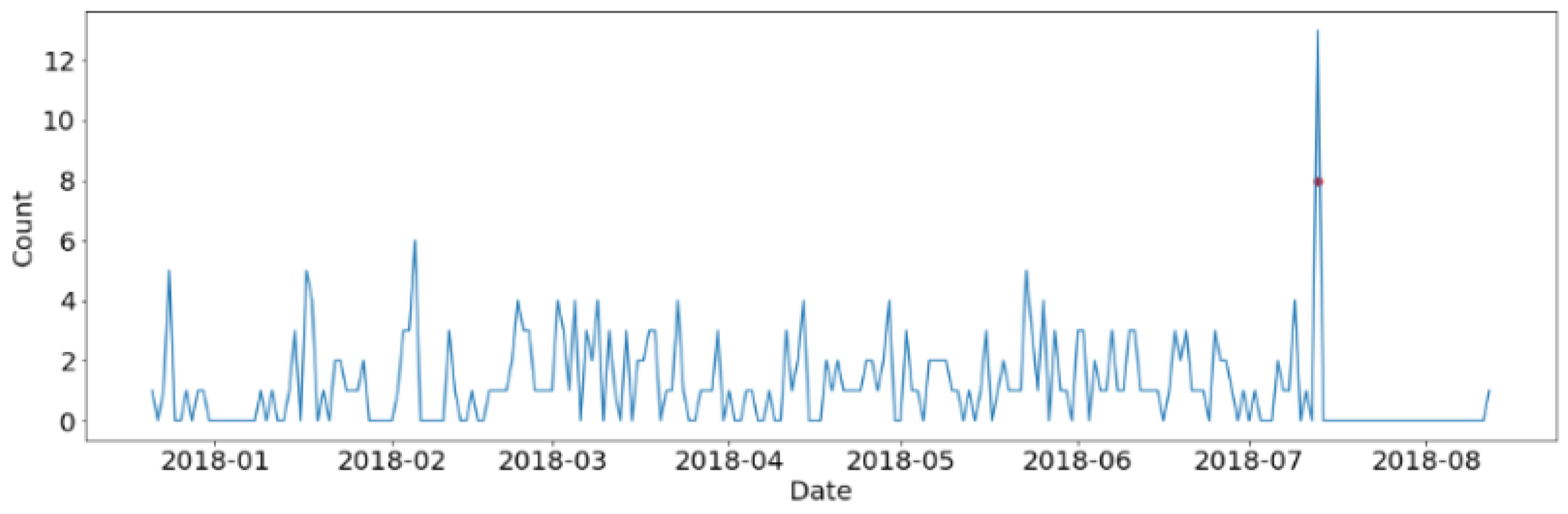
- In order to detect fraud in the testing set, the errors are calculated in terms of difference between the predicted and actual daily count of transactions. Then, the Z-Scores are computed and used to flag the anomalies (i.e., the frauds). The Z-Score is calculated as , where x is the prediction error on the daily count of transaction in the testing set. and are the mean and the variance based on the errors of in-sample prediction on the basis of the training set using our model. If the Z-Score is greater than a threshold, the day is flagged as anomalous (i.e., as fraud).
3. Application to Dataset
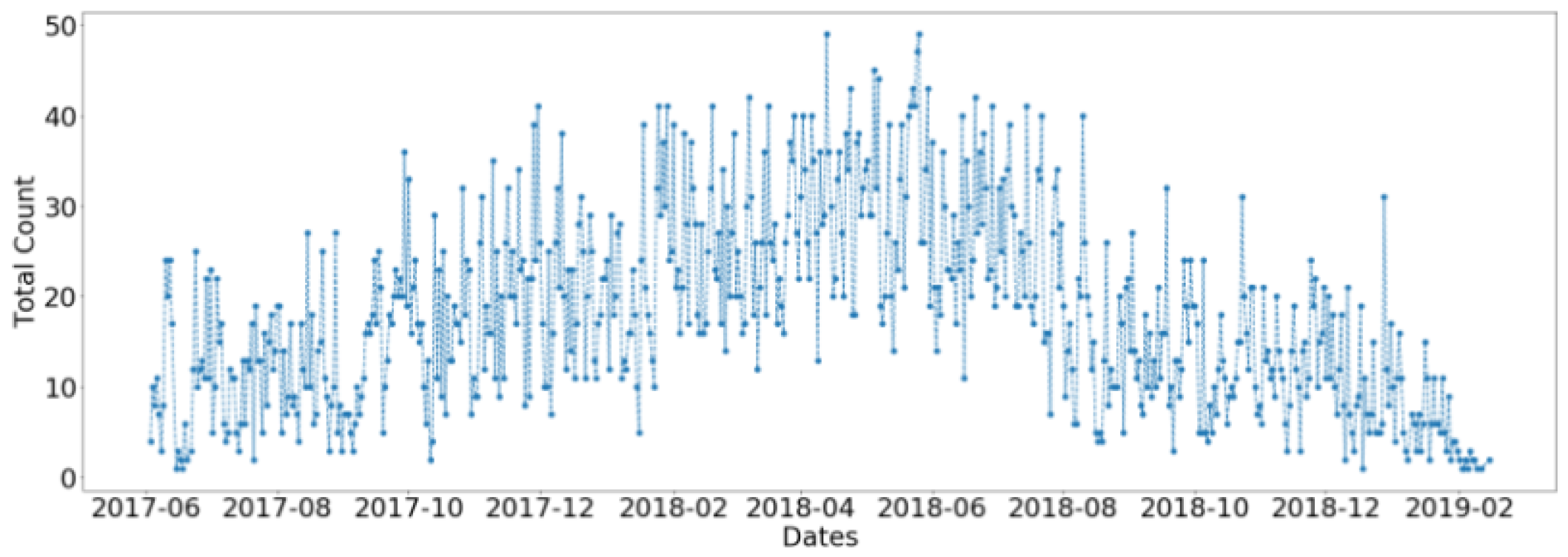
3.1. Dataset Description
3.2. Application of ARIMA Model for Daily Counts of Transactions
3.3. Benchmark Models
3.3.1. Box Plot
3.3.2. Local Outlier Factor (LOF)
3.3.3. Isolation Forest
3.3.4. K-Means
- 1.
- For each point :
- (a)
- Find the nearest centroid . K-means computes the Euclidean distance between each point and centroid . This approach is often called minimising the inertia of the clusters [21] and can be defined as follows:where n is the number of points x and i is the number of centroids c.
- (b)
- Assign instance to cluster J.
- 2.
- For each cluster
- (a)
- Compute the new centroid . This is achieved by calculating the mean from each point x to the centroid x of the cluster J to which is was firstly assigned.
- 3.
- Stop when convergence is reached; that is, there are no more changes after the iterations.
4. Results
5. Conclusions
- 1.
- It works better when there is a significant number of frauds occurring on the same day. This is often the case, as fraudsters are known to take advantage of the time they have before the card is blocked to make several fraudulent transactions in a short time span [13].
- 2.
- It presents the best precision; i.e., it reduces the number of false positives compared to the benchmark models.
- 3.
- It takes into account the dynamic spending behaviour of the customer by using the rolling windows.
Funding
References
- Bank, E.C. Fifth Report on Card Fraud; European Central Bank: Frankfurt am Main, Germany, 2019. [Google Scholar]
- Nilson. The Nilson Report|News and Statistics for Card and Mobile Payment Executives. Available online: Nilsonreport.com (accessed on 1 June 2019).
- Maniraj, S.P. Credit Card Fraud Detection using Machine Learning and Data Science. Int. J. Eng. Res. Technol. 2019, 8, 110–115. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, Y.; Tushar, L.; Shubhra, D. Credit Dard Fraud Detection Using Local Outlier Factor. Int. J. Pure Appl. Math. 2018, 118, 229–234. [Google Scholar]
- Pozzolo, A.D. Learned lessons in credit card fraud detection from a practitioner perspective. Expert Syst. Appl. 2014, 41, 4915–4928. [Google Scholar] [CrossRef]
- Singh, D.; Vardhan, S.; Agrawal, N. Credit Card Fraud Detection Analysis. Int. Res. J. Eng. Technol. (IRJET) 2018, 5, 1600–1603. [Google Scholar]
- Khare, N.; Sait, S.Y. Credit Card Fraud Detection Using Machine Learning Models and Collating Machine Learning Models. Int. J. Pure Appl. Math. 2018, 118–120, 825–838. [Google Scholar]
- Varmedja, D. Credit Card Fraud Detection—Machine Learning methods. In Proceedings of the 18th International Symposium INFOTEH-JAHORINA, Jahorina, Bosnia and Herzegovina, 20–22 March 2019. [Google Scholar]
- Roy, A. Deep learning detecting fraud in credit card transactions. In Proceedings of the 2018 Systems and Information Engineering Design Symposium, Charlotteville, VA, USA, 27 April 2018; pp. 129–134. [Google Scholar]
- Adhikari, R.; Agrawal, R.K. An Introductory Study on Time Series Modeling and Forecasting. arXiv 2013, arXiv:1302.6613. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Azrak, R.; Melard, G. Exact Maximum Likelihood Estimation for Extended ARIMA Models; Université Libre de Bruxelles Institutional Repository: Brussels, Belgium, 2013. [Google Scholar]
- Seyedhossein, L.; Hashemi, M.R. Mining information from credit card time series for timelier fraud detection. Int. J. Inf. Commun. Technol. 2010, 2, 619–624. [Google Scholar]
- Ounacer, S. Using Isolation Forest in anomaly detection: The case of credit card transactions. Period. Eng. Nat. Sci. (PEN) 2018, 6, 394. [Google Scholar] [CrossRef] [Green Version]
- Williamson, D.F. The Box Plot: A Simple Visual Method to Interpret Data. Ann. Intern. Med. 1989, 110, 916–921. [Google Scholar] [CrossRef] [PubMed]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. ACM SIGMOD Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. 2011, 12, 2825–2830. [Google Scholar]
- John, H.; Naaz, S. Credit Card Fraud Detection using Local Outlier Factor and Isolation Forest. Int. J. Comput. Sci. Eng. 2019, 7, 1060–1064. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 8th IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; Volume 7, pp. 413–422. [Google Scholar]
- Kubat, M. An Introduction to Machine Learning; Springer: Berlin, Germany, 2015. [Google Scholar]
- Dalatu, P.I. Time Complexity of K-Means and K-Medians Clustering Algorithms in Outliers Detection. Glob. J. Pure Appl. Math. 2018, 12, 4405–4418. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms: Popular Algorithms for Data Science and Machine Learning; Packt: Birmingham, UK, 2018. [Google Scholar]

| Legitimate | Fraud | Total | |
|---|---|---|---|
| Number | 11,384 | 87 | 11,471 |
| Percentage | 99.24% | 0.76% | 100% |
| Time Series ID | # Days in Train | # Days in Test | Fraud Proportion |
|---|---|---|---|
| 0 | 192 | 83 | 1/14 |
| 4 | 193 | 84 | 1/3 |
| 5 | 192 | 83 | 1/16 |
| 7 | 186 | 80 | 1/11 |
| 8 | 131 | 57 | 3/15 |
| 9 | 164 | 71 | 8/21 |
| 10 | 193 | 84 | 4/17 |
| 15 | 191 | 82 | 1/11 and 1/2 |
| 17 | 119 | 51 | 2/12 |
| t-Statistic | −8.73162539099 |
| p-value | 3.180176629 × 10 |
| METRICS | ARIMA | BOX-PLOT | LOF | IF | K-MEANS |
|---|---|---|---|---|---|
| Precision | 50% | 43.98% | 8.4% | 25.01% | 21.82% |
| Recall | 66.67% | 72.22% | 66.67%, | 72.22% | 83.33% |
| F-Measure | 55.56% | 52.22%, | 14.04% | 32.56% | 28.95% |
| METRICS | ARIMA | BOX-PLOT | LOF | IF | K-MEANS |
|---|---|---|---|---|---|
| Precision | 34.29% | 28.96% | 6.41% | 19.94% | 22.51% |
| Recall | 42.03% | 60.54% | 69.57%, | 64.09% | 68.16% |
| F-Measure | 36.19% | 34.91%, | 11.17% | 24.82% | 26.81% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschini, G.; Houssou, R.; Bovay, J.; Robert-Nicoud, S. Anomaly and Fraud Detection in Credit Card Transactions Using the ARIMA Model. Eng. Proc. 2021, 5, 56. https://doi.org/10.3390/engproc2021005056
Moschini G, Houssou R, Bovay J, Robert-Nicoud S. Anomaly and Fraud Detection in Credit Card Transactions Using the ARIMA Model. Engineering Proceedings. 2021; 5(1):56. https://doi.org/10.3390/engproc2021005056
Chicago/Turabian StyleMoschini, Giulia, Régis Houssou, Jérôme Bovay, and Stephan Robert-Nicoud. 2021. "Anomaly and Fraud Detection in Credit Card Transactions Using the ARIMA Model" Engineering Proceedings 5, no. 1: 56. https://doi.org/10.3390/engproc2021005056
APA StyleMoschini, G., Houssou, R., Bovay, J., & Robert-Nicoud, S. (2021). Anomaly and Fraud Detection in Credit Card Transactions Using the ARIMA Model. Engineering Proceedings, 5(1), 56. https://doi.org/10.3390/engproc2021005056





