A Hypothesis Test for the Goodness-of-Fit of the Marginal Distribution of a Time Series with Application to Stablecoin Data †
Abstract
:1. Introduction
2. Empirical Survival Jensen–Shannon Divergence
3. A Bootstrap-Based Goodness-of-Fit Hypothesis Test
| Algorithm 1: Parametric-Boostrap(). |
| 1. begin 2. Initialise and as the vector, , of m zeros; 3. Let n be the number of values in ; 4. Let ; 5. Let ; 6. for to m do 7. Generate a bootstrap sample , 8. where is generated from an AR(1) process with innovations derived from D with parameters ; 9. Let ; 10. Let ; 11. Let ; 12. end for 13. return and sorted in ascending order. 14. end |
4. Cryptocurrencies and Heavy Tails
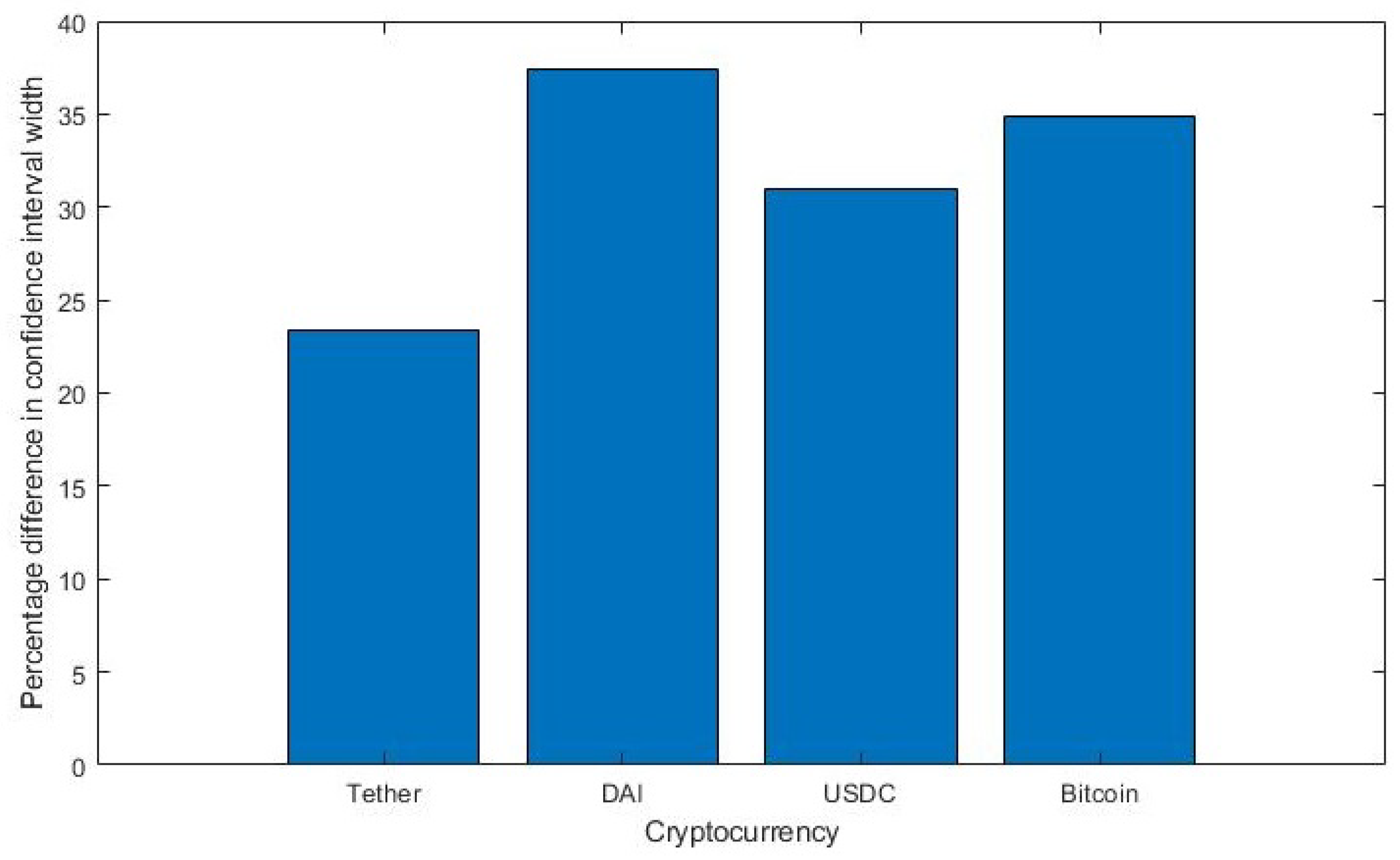
5. Application of the Goodness-Of-Fit Hypothesis Test to Cryptocurrencies
6. Concluding Remarks
References
- Levene, M.; Kononovicius, A. Empirical survival Jensen–Shannon divergence as a goodness-of-fit measure for maximum likelihood estimation and curve fitting. Commun. Stat.-Simul. Comput. 2019. [Google Scholar] [CrossRef] [Green Version]
- Ventura, V. Bootstrap Tests of Hypotheses. In Analysis of Parallel Spike Trains; Springer Series in Computational Neuroscience; Grün, S., Rotter, S., Eds.; Springer: Boston, MA, USA, 2010; Volume 7, Chapter 18; pp. 383–398. [Google Scholar]
- Pewsey, A. Parametric bootstrap edf-based goodness-of-fit testing for sinh–arcsinh distributions. TEST 2018, 27, 147–172. [Google Scholar] [CrossRef]
- Enders, W. Applied Econometric Time Series, 4th ed.; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Chatfield, C.; Xing, H. The Analysis of Time Series: An Introduction with R, 7th ed.; Text in Statistical Science; Chapman & Hall: London, UK, 2019. [Google Scholar]
- Sidorenko, E. Stablecoin as a new financial instrument. In Proceedings of International Scientific Conference on Digital Transformation of the Economy: Challenges, Trends, New Opportunities; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Judmayer, A.; Stifter, N.; Krombholz, K.; Weippl, E.; Bertino, E.; Sandhu, R. Blocks and Chains: Introduction to Bitcoin, Cryptocurrencies, and Their Consensus Mechanisms; Synthesis Lectures on Information Security; Privacy, and Trust, Morgan & Claypool Publishers: San Francisco, CA, USA, 2017. [Google Scholar]
- Kakinaka, S.; Umeno, K. Characterizing cryptocurrency market with Lévy’s stable distributions. J. Phys. Soc. Jpn. 2020, 89, 024802-1–024802-13. [Google Scholar] [CrossRef] [Green Version]
- Nolan, J. Univariate Stable Distributions: Models for Heavy Tailed Data; Springer Series in Operations Research and Financial Engineering; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Gibbons, J.; Chakraborti, S. Nonparametric Statistical Inference, 6th ed.; Marcel Dekker: New York, NY, USA, 2021. [Google Scholar]
- Cornea-Madeira, A.; Davidson, R. A parametric bootstrap for heavy-tailed distributions. Econom. Theory 2015, 31, 449–470. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; McLeod, A. Improved Peňa–Rodriguez portmanteau test. Comput. Stat. Data Anal. 2006, 51, 1731–1738. [Google Scholar] [CrossRef]
- Gallagher, C. A method for fitting stable autoregressive models using the autocovariation function. Stat. Probab. Lett. 2001, 53, 381–390. [Google Scholar] [CrossRef]
- Ouadjed, H.; Mami, T. Estimating the tail conditional expectation of Walmart stock data. Croat. Oper. Res. Rev. 2020, 11, 95–106. [Google Scholar] [CrossRef]
- Hesterberg, T. what teachers should know about the bootstrap: Resampling in the undergraduate statistics curriculum. Am. Stat. 2015, 69, 371–386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chernick, M. Bootstrap Methods: A Guide for Practitioners and Researchers, 2nd ed.; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- DeCarlo, L. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292–307. [Google Scholar] [CrossRef]
- Veillette, M. Alpha-Stable Distributions in MATLAB. 2015. Available online: http://math.bu.edu/people/mveillet/html/alphastablepub.html (accessed on 1 June 2021).
- Koutrouvelis, I. An iterative procedure for the estimation of the parameters of stable laws. Commun. Stat.-Simul. Comput. 1981, 10, 17–28. [Google Scholar] [CrossRef]
- Liu, X. Comparing sample size requirements for significance tests and confidence intervals. Couns. Outcome Res. Eval. 2013, 4, 3–12. [Google Scholar] [CrossRef]


| Currency | #Values | From | Until | Closing Rate |
|---|---|---|---|---|
| Tether | 1264 | 06 January 2017 | 15 November 2020 | daily |
| DAI | 362 | 20 November 2019 | 15 November 2020 | daily |
| USDC | 772 | 28 September 2018 | 15 November 2020 | daily |
| Bitcoin | 8929 | 01 January 2020 | 07 January 2021 | hourly |
| Currency | Excess Kurtosis |
|---|---|
| Tether | 86.0207 |
| DAI | 34.6573 |
| USDC | 10.1905 |
| Bitcoin | 59.7350 |
| Fitted Parameters for Stable Distribution | ||||
|---|---|---|---|---|
| Currency | ||||
| Tether | 1.0111 | 0.0019 | 0.0011 | 0.0001 |
| DAI | 1.1953 | 0.0821 | 0.0016 | 0.0003 |
| USDC | 1.2259 | 0.0125 | 0.0003 | 0.0000 |
| Bitcoin | 1.2261 | 0.0909 | 27.9685 | 7.3644 |
| Currency | |
|---|---|
| Tether | −0.3604 |
| DAI | −0.4045 |
| USDC | −0.4948 |
| Bitcoin | −0.0504 |
| Parametric Bootstrap for Assuming a Stable Distribution | ||||||
|---|---|---|---|---|---|---|
| Currency | LB of CI | UB of CI | Width of CI | Mean | STD | |
| Tether | 0.0006 | 0.0232 | 0.0226 | 0.0090 | 0.0198 | 0.0741 |
| DAI | 0.0030 | 0.0345 | 0.0315 | 0.0156 | 0.0188 | 0.0096 |
| USDC | 0.0013 | 0.0247 | 0.0234 | 0.0119 | 0.0133 | 0.0063 |
| Bitcoin | 0.0004 | 0.0066 | 0.0062 | 0.0061 | 0.0036 | 0.0016 |
| Parametric Bootstrap for Assuming a Stable Distribution | ||||||
|---|---|---|---|---|---|---|
| Currency | LB of CI | UB of CI | Width of CI | Mean | STD | |
| Tether | 0.0014 | 0.0308 | 0.0294 | 0.0139 | 0.0289 | 0.0996 |
| DAI | 0.0029 | 0.0532 | 0.0503 | 0.0358 | 0.0299 | 0.0136 |
| USDC | 0.0035 | 0.0374 | 0.0339 | 0.0219 | 0.0210 | 0.0093 |
| Bitcoin | 0.0008 | 0.0103 | 0.0095 | 0.0088 | 0.0057 | 0.0025 |
| Parametric Bootstrap Results Assuming a Normal Distribution | ||||||
|---|---|---|---|---|---|---|
| Currency | LB- | UB- | LB-K | UB-K | ||
| Tether | 0.0001 | 0.0132 | 0.1440 | 0.0004 | 0.0182 | 0.2162 |
| DAI | 0.0003 | 0.0240 | 0.1160 | 0.0006 | 0.0330 | 0.1665 |
| USDC | 0.0002 | 0.0147 | 0.0830 | 0.0002 | 0.0227 | 0.1330 |
| Bitcoin | 0.0001 | 0.0067 | 0.1218 | 0.0000 | 0.0085 | 0.1708 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levene, M. A Hypothesis Test for the Goodness-of-Fit of the Marginal Distribution of a Time Series with Application to Stablecoin Data. Eng. Proc. 2021, 5, 10. https://doi.org/10.3390/engproc2021005010
Levene M. A Hypothesis Test for the Goodness-of-Fit of the Marginal Distribution of a Time Series with Application to Stablecoin Data. Engineering Proceedings. 2021; 5(1):10. https://doi.org/10.3390/engproc2021005010
Chicago/Turabian StyleLevene, Mark. 2021. "A Hypothesis Test for the Goodness-of-Fit of the Marginal Distribution of a Time Series with Application to Stablecoin Data" Engineering Proceedings 5, no. 1: 10. https://doi.org/10.3390/engproc2021005010
APA StyleLevene, M. (2021). A Hypothesis Test for the Goodness-of-Fit of the Marginal Distribution of a Time Series with Application to Stablecoin Data. Engineering Proceedings, 5(1), 10. https://doi.org/10.3390/engproc2021005010






