Cost Estimation and Parametric Optimization for TIG Welding Joints in Dissimilar Metals Using Linear Regression Algorithm †
Abstract
:1. Introduction
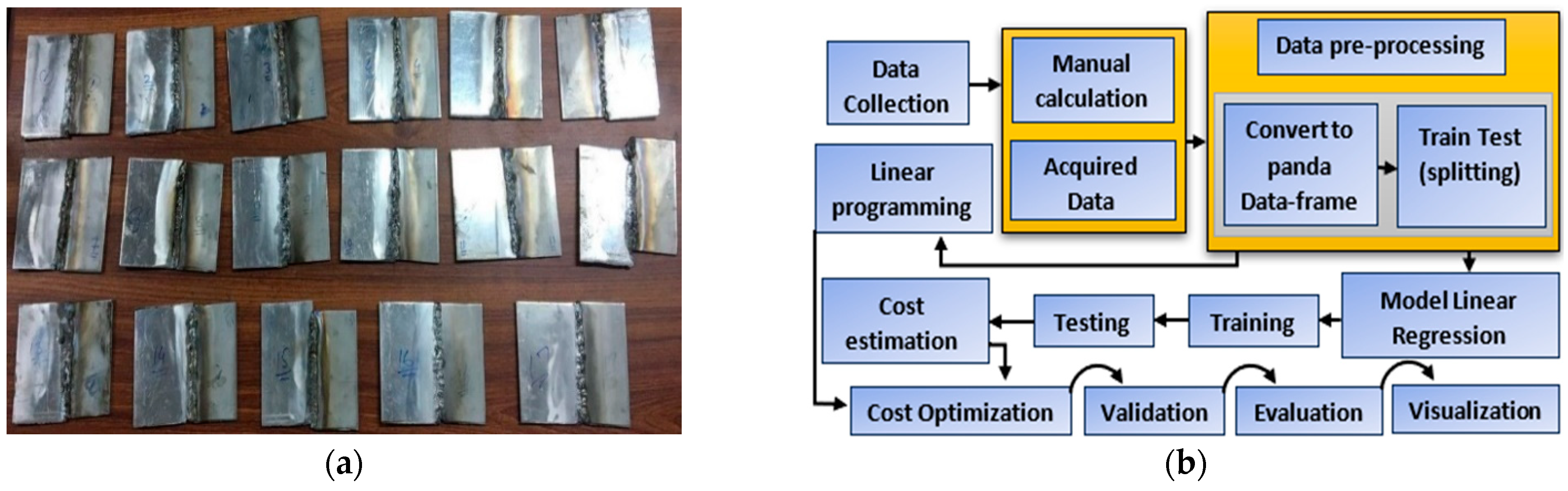
2. Methodology
2.1. Physical Experimentation
2.2. Experimentation Using Machine Learning
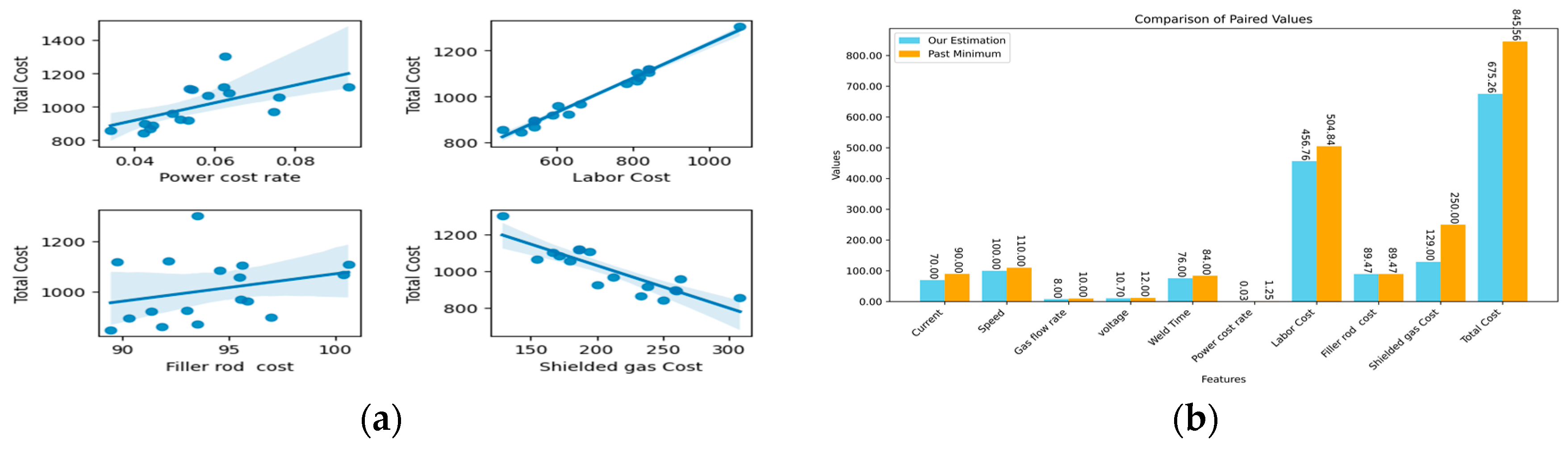
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El-Kassas, A.M.; Sabry, I. A Comparison between FSW, MIG and TIG Based on Total Cost Estimation for Aluminum Pipes. Eur. J. Adv. Eng. Technol. 2017, 4, 158–163. [Google Scholar]
- Vasudevan, M.; Bhaduri, A.K.; Raj, B.; Kalvala, P. Genetic-algorithm-based computational models for optimizing the process parameters of A-TIG welding to achieve target bead geometry in type 304 L(N) and 316 L(N) stainless steels. Mater. Manuf. Process. 2007, 22, 641–649. [Google Scholar] [CrossRef]
- Patil, P.C.; Shelke, R.D. Review on Welding Parameter Effects on Tig Welding of Aluminium Alloy. Int. J. Eng. Res. Gen. Sci. 2015, 3, 1479–1486. [Google Scholar]
- Dutta, P.; Pratihar, D.K. Modeling of TIG welding process using conventional regression analysis and neural network-based approaches. J. Mater. Process. Technol. 2007, 186, 56–68. [Google Scholar] [CrossRef]

| Sr no. | I (Amp) | S mm/min | F.G L/min | V Volts | WT min | PC (PKR) | LC (PKR) | FRC (PKR) | SHC (PKR) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 110 | 9 | 12.7 | 90 | 1.260587 | 540.90 | 96.96 | 259.2 |
| 2 | 70 | 110 | 8 | 12.2 | 135 | 1.601271 | 811.35 | 100.62 | 194.4 |
| 3 | 80 | 110 | 9 | 12.6 | 136 | 1.890137 | 817.36 | 94.57 | 172 |
| 4 | 80 | 100 | 10 | 13.1 | 90 | 1.300493 | 540.90 | 93.51 | 233 |
| 5 | 70 | 120 | 9 | 12 | 140 | 1.621819 | 841.40 | 95.64 | 167 |
| 6 | 80 | 110 | 9 | 12.1 | 76 | 1.014902 | 456.76 | 91.87 | 308 |
| 7 | 80 | 120 | 10 | 13.2 | 105 | 1.528905 | 631.05 | 93.05 | 200 |
| 8 | 70 | 110 | 10 | 13.3 | 135 | 1.732898 | 811.35 | 100.40 | 155 |
| 9 | 80 | 120 | 8 | 12 | 140 | 1.853209 | 841.40 | 92.19 | 187 |
| 10 | 90 | 100 | 9 | 11.9 | 90 | 1.328933 | 540.90 | 90.31 | 260 |
| 11 | 80 | 110 | 9 | 14.7 | 98 | 1.589388 | 588.98 | 91.37 | 238 |
| 12 | 70 | 100 | 9 | 10.7 | 180 | 1.858868 | 1081.8 | 93.55 | 129 |
| 13 | 90 | 110 | 8 | 16 | 140 | 2.781452 | 841.40 | 89.74 | 187 |
| 14 | 90 | 110 | 10 | 12 | 84 | 1.251117 | 504.84 | 89.47 | 250 |
| 15 | 80 | 110 | 9 | 15.8 | 130 | 2.26605 | 781.30 | 95.50 | 180 |
| 16 | 80 | 100 | 8 | 13.3 | 100 | 1.467082 | 601.00 | 95.85 | 263 |
| 17 | 90 | 120 | 9 | 16.3 | 110 | 2.224834 | 661.10 | 95.55 | 212 |
| Total | 28.57194 | 11,893.79 | 1600.15 | 3594.6 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhtar, G.A.; Shehzadi, S.; Sajid, A.; Laar, J.M.T.; Taqi, S.A.; Usman, R.M.; Hasnain, F.u. Cost Estimation and Parametric Optimization for TIG Welding Joints in Dissimilar Metals Using Linear Regression Algorithm. Eng. Proc. 2023, 45, 50. https://doi.org/10.3390/engproc2023045050
Mukhtar GA, Shehzadi S, Sajid A, Laar JMT, Taqi SA, Usman RM, Hasnain Fu. Cost Estimation and Parametric Optimization for TIG Welding Joints in Dissimilar Metals Using Linear Regression Algorithm. Engineering Proceedings. 2023; 45(1):50. https://doi.org/10.3390/engproc2023045050
Chicago/Turabian StyleMukhtar, Ghulam Ameer, Sana Shehzadi, Abdullah Sajid, Jam Muhammad Talha Laar, Syed Ali Taqi, Rana Muhammad Usman, and Fakhar ul Hasnain. 2023. "Cost Estimation and Parametric Optimization for TIG Welding Joints in Dissimilar Metals Using Linear Regression Algorithm" Engineering Proceedings 45, no. 1: 50. https://doi.org/10.3390/engproc2023045050
APA StyleMukhtar, G. A., Shehzadi, S., Sajid, A., Laar, J. M. T., Taqi, S. A., Usman, R. M., & Hasnain, F. u. (2023). Cost Estimation and Parametric Optimization for TIG Welding Joints in Dissimilar Metals Using Linear Regression Algorithm. Engineering Proceedings, 45(1), 50. https://doi.org/10.3390/engproc2023045050






