Intelligent RGV Scheduling Model Considering Advanced Movement under Repeated Single-Cycle Jobs †
Abstract
:1. Introduction
2. Intelligent RGV Scheduling Model Considering Advanced Movement
2.1. Hypothesis
- Due to regular preventive maintenance, the probability of failure of CNCs and RGVs during the production process is extremely low;
- Only one production process is completed for each material.
2.2. Notations
2.3. Model Description
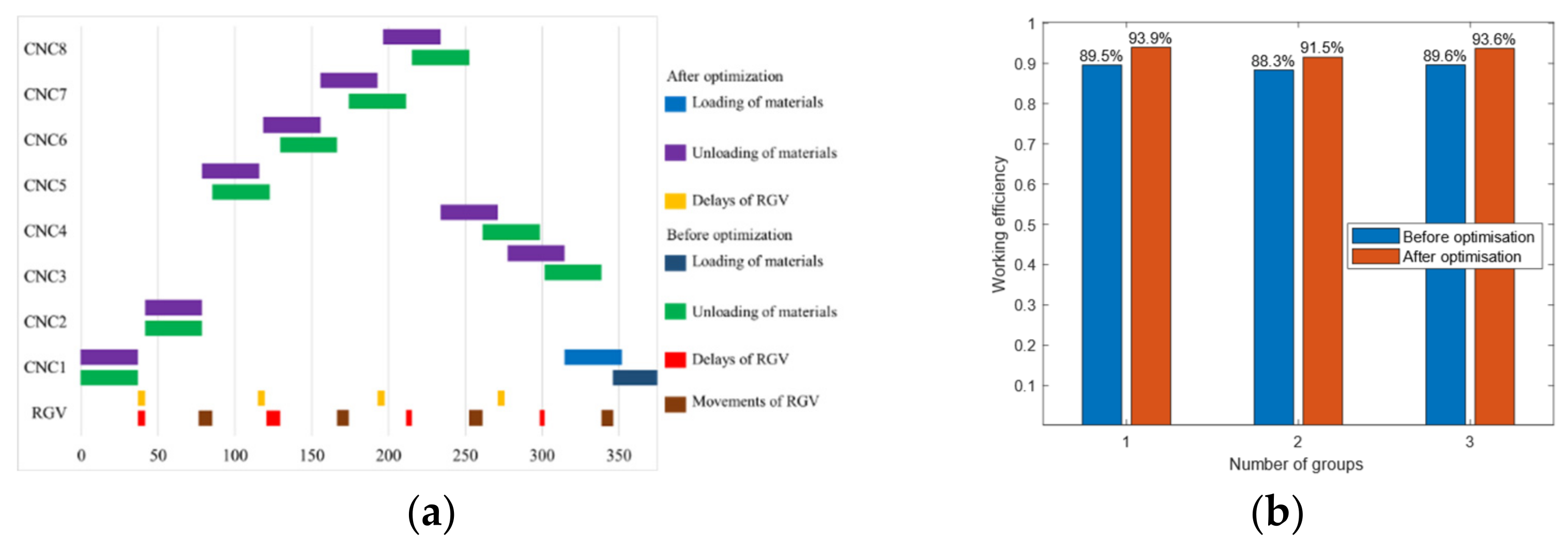
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, G.B.; Zhang, J. A dynamic scheduling method based on improved rolling time-domain optimization strategy. J. Mech. Eng. 2013, 49, 182–190. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Zhang, D. Research on dynamic scheduling of RGV based on genetic algorithm. Lift. Transp. Mach. 2012, 6, 20–23. [Google Scholar]
- Liu, F.; Xing, K.; Zhang, Y. Dynamic scheduling strategy for random fault intelligent RGV based on optimal path. Electron. Technol. Softw. Eng. 2018, 23, 160. [Google Scholar]
- Han, C.G.; Mei, Z.Y. Mathematical modelling of dynamic scheduling strategy problem for intelligent RGVs. Math. Model. Its Appl. 2019, 8, 53–65+83. [Google Scholar]

| Notations | Definitions | Unit |
|---|---|---|
| Whether the CNC is processing the material; 1 if yes, 0 otherwise. | ||
| Whether RGV completes its left and right CNC loading and unloading work; 0 if yes, 1 otherwise. | ||
| Work efficiency of the system in a single cycle. | ||
| Processing time for each raw material. | s | |
| The time for RGV to service the entire CNC. | s | |
| The maximum number of finished products that can be produced in the time period. | ||
| Loading and unloading time of the CNC single job. | s | |
| Total time of the system working at once. | s | |
| Waiting time of the CNC before processing the material. | s | |
| RGV cleaning time for a processed material. | s | |
| RGV moves units of distance on the track . | s | |
| The number of CNC. | s | |
| The moving time for the RGV when the CNC is processing the material. | s | |
| The waiting time for the RGV when the CNC is processing the material. | s | |
| The loading start time of the material produced by the CNC. | s | |
| The unloading start time of the material produced by the CNC. | s | |
| Time required for one CNC loading and unloading for odd numbered CNCs. | s | |
| Time required for one CNC loading and unloading for even numbered CNCs. | s |
| System Operation Parameters | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| The time for an RGV to move 1 unit () | 20 | 23 | 18 |
| The time for an RGV to move 2 units () | 33 | 41 | 32 |
| The time for an RGV to move 3 units () | 46 | 59 | 46 |
| The time for a CNC to complete a one-step material () | 560 | 580 | 545 |
| Time required for one CNC loading and unloading for odd numbered CNCs () | 400 | 280 | 455 |
| Time required for one CNC loading and unloading for even numbered CNCs () | 378 | 500 | 182 |
| The time for an RGV to complete the cleaning operation of a material () | 28 | 30 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Xu, Z.; Qi, F.; Yin, Z. Intelligent RGV Scheduling Model Considering Advanced Movement under Repeated Single-Cycle Jobs. Eng. Proc. 2023, 45, 33. https://doi.org/10.3390/engproc2023045033
Meng Y, Xu Z, Qi F, Yin Z. Intelligent RGV Scheduling Model Considering Advanced Movement under Repeated Single-Cycle Jobs. Engineering Proceedings. 2023; 45(1):33. https://doi.org/10.3390/engproc2023045033
Chicago/Turabian StyleMeng, Yinghao, Zihao Xu, Faqun Qi, and Zhen Yin. 2023. "Intelligent RGV Scheduling Model Considering Advanced Movement under Repeated Single-Cycle Jobs" Engineering Proceedings 45, no. 1: 33. https://doi.org/10.3390/engproc2023045033
APA StyleMeng, Y., Xu, Z., Qi, F., & Yin, Z. (2023). Intelligent RGV Scheduling Model Considering Advanced Movement under Repeated Single-Cycle Jobs. Engineering Proceedings, 45(1), 33. https://doi.org/10.3390/engproc2023045033





