Real-Time Vehicle Lateral Dynamics Estimation Using State Observer and Adaptive Filter †
Abstract
:1. Introduction
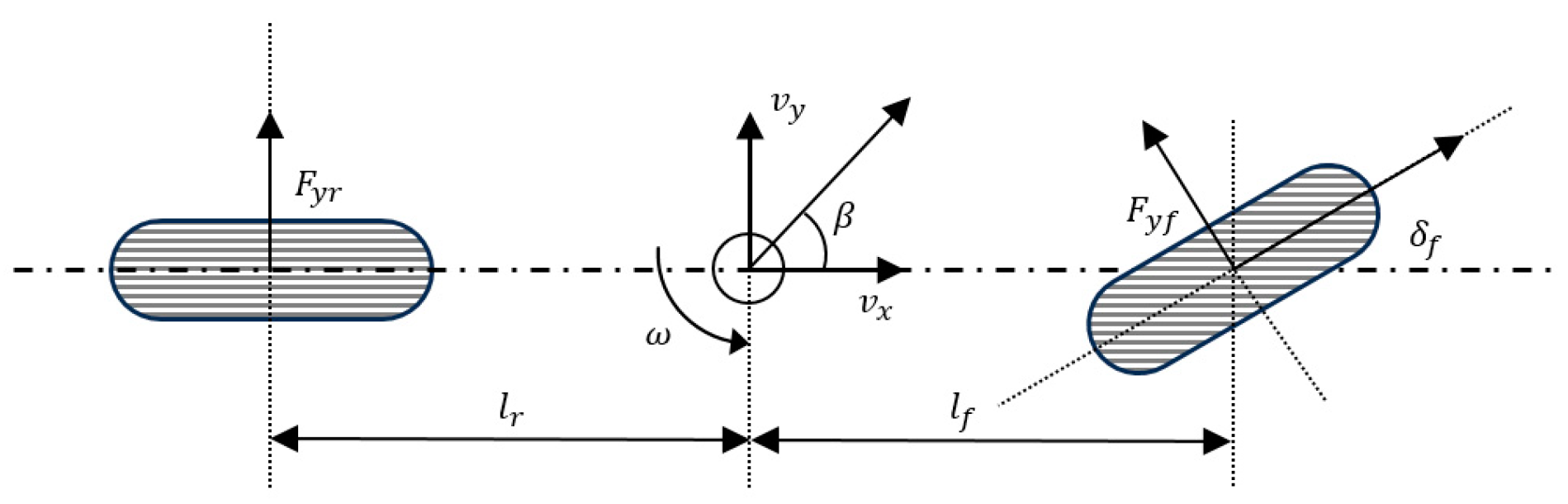
2. Mathematical Modeling
3. Roll Angle and Side-Slip Angle Estimation
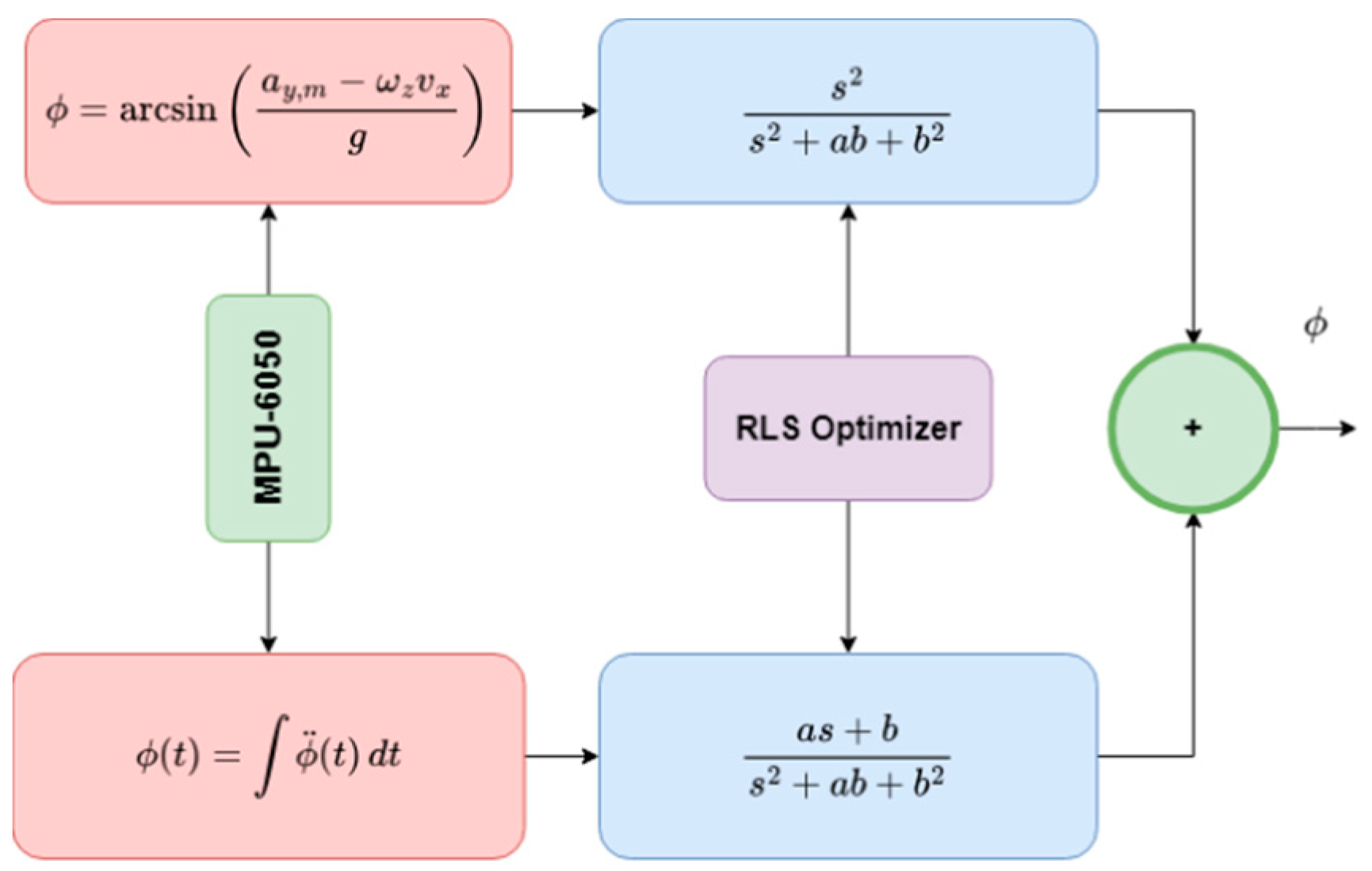
3.1. Adaptive Complementary Filter for Roll Angle of Ground Vehicle
3.2. Side-Slip Angle Estimation
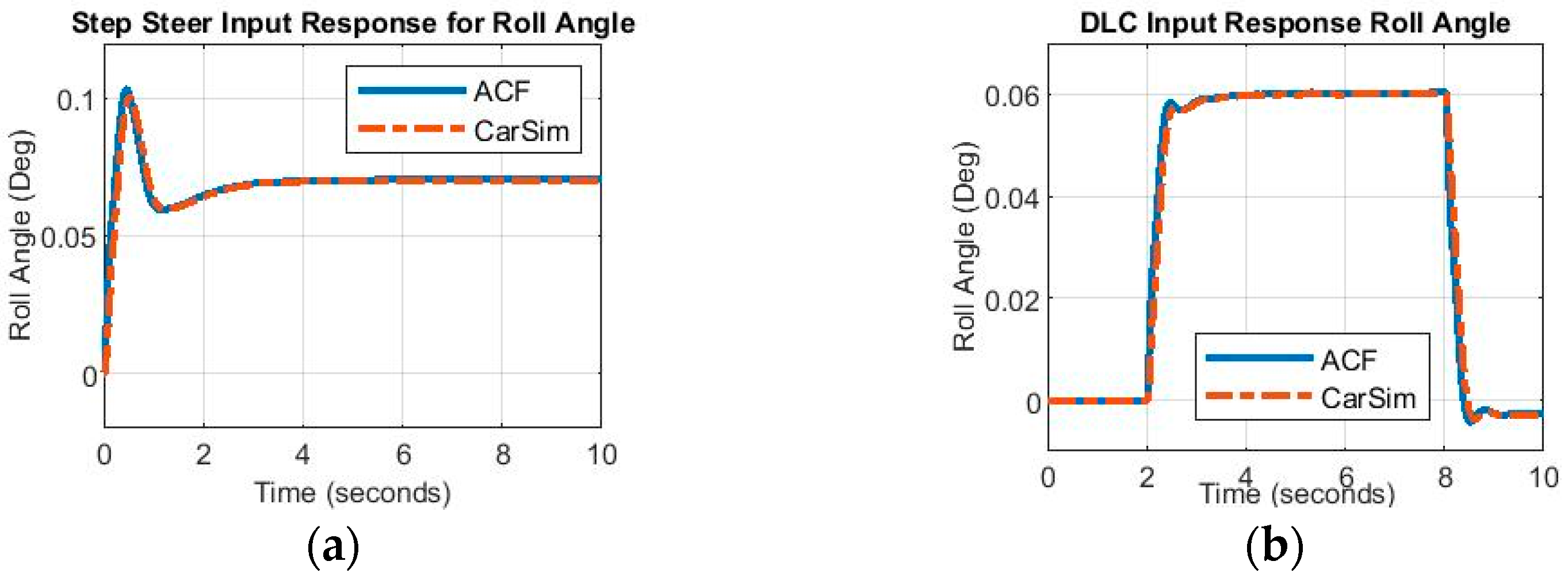
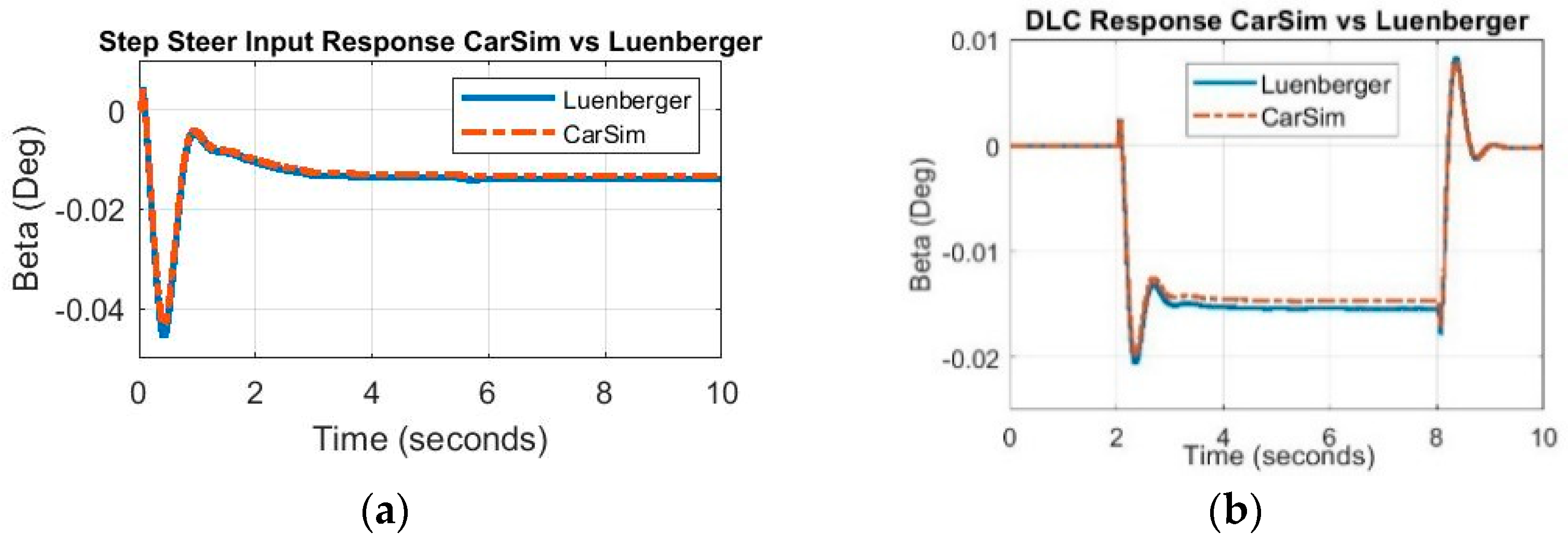
4. Experiment and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Wang, Z.; Zou, C.; Drugge, L.; Nybacka, M. Advanced Vehicle State Monitoring: Evaluating Moving Horizon Estimators and Unscented Kalman Filter. IEEE Trans. Veh. Technol. 2019, 68, 5430–5442. [Google Scholar] [CrossRef]
- Katriniok, A.; Abel, D. Adaptive EKF-Based Vehicle State Estimation with Online Assessment of Local Observability. IEEE Trans. Control. Syst. Technol. 2016, 24, 1368–1381. [Google Scholar] [CrossRef]
- Ungoren, A.Y.; Peng, H.; Tseng, H.E. A study of lateral speed estimation methods. Int. J. Veh. Auto. 2004, 2, 126–144. [Google Scholar] [CrossRef]
- Fukada, Y. Slip-angle estimation for vehicle stability control. Veh. Syst. Dyn. 1999, 32, 375–388. [Google Scholar] [CrossRef]
- Nam, K.; Oh, S.; Fujimoto, H.; Hori, Y. Estimation of sideslip and roll angles of electric vehicles using lateral tire force sensors through RLS and Kalman filter approaches. IEEE Trans. Ind. Electron. 2013, 60, 988–1000. [Google Scholar] [CrossRef]
- Zhang, B.; Du, H.; Lam, J.; Zhang, N.; Li, W. A novel observer design for simultaneous estimation of vehicle steering angle and sideslip angle. IEEE Trans. Ind. Electron. 2016, 63, 4357–4366. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Q.; Qiu, J. Robust ∞ filtering for vehicle sideslip angle estimation with sampled-data measurements. Trans. Inst. Meas. Control 2017, 39, 1059–1070. [Google Scholar] [CrossRef]
- Farrelly, J.; Wellstead, P. Estimation of vehicle lateral velocity. In Proceedings of the 1996 IEEE International Conference on Control Applications IEEE International Conference on Control Applications held together with IEEE International Symposium on Intelligent Contro, Dearborn, MI, USA, 15–18 November 1996; pp. 552–557. [Google Scholar]
- Lee, H. Reliability indexed sensor fusion and its application to vehicle velocity estimation. J. Dyn. Syst. Meas. Control 2006, 128, 236–243. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamal Mazhar, M.; Khan, M.J.; Kallu, K.D.; Ayaz, Y. Real-Time Vehicle Lateral Dynamics Estimation Using State Observer and Adaptive Filter. Eng. Proc. 2023, 45, 27. https://doi.org/10.3390/engproc2023045027
Kamal Mazhar M, Khan MJ, Kallu KD, Ayaz Y. Real-Time Vehicle Lateral Dynamics Estimation Using State Observer and Adaptive Filter. Engineering Proceedings. 2023; 45(1):27. https://doi.org/10.3390/engproc2023045027
Chicago/Turabian StyleKamal Mazhar, Malik, Muhammad Jawad Khan, Karam Dad Kallu, and Yasar Ayaz. 2023. "Real-Time Vehicle Lateral Dynamics Estimation Using State Observer and Adaptive Filter" Engineering Proceedings 45, no. 1: 27. https://doi.org/10.3390/engproc2023045027
APA StyleKamal Mazhar, M., Khan, M. J., Kallu, K. D., & Ayaz, Y. (2023). Real-Time Vehicle Lateral Dynamics Estimation Using State Observer and Adaptive Filter. Engineering Proceedings, 45(1), 27. https://doi.org/10.3390/engproc2023045027






