Abstract
This article discusses the extent of the spread of contamination in water distribution networks which may enter through a pipe leak, and the decay rate of chlorine for a specified design duration. A comprehensive water quality analysis is performed using EPANet 2.2 for the spread of contamination and chlorine decay. The results show that a contaminant entering at the highest point of the network would pollute the whole network whereas the effect of such a contaminant would be limited if it enters at the lowest location. Also, the initial chlorine concentration is found to be more for such critical nodes which are higher in elevation, although the decay rate remains the same. The research proves to be beneficial for the management of water distribution through pipe networks against contaminants for maintaining public health.
1. Introduction
A leak in the water supply pipe may cause contamination to enter into the network which presents serious harm to living beings [1,2,3]. Pipe leakage may occur due to corrosion of pipe material, incorrect laying of pipes, or any impact or excessive loads on the pipes [4,5]. The contamination which enters into the pipe may be of two types namely, reactive or non-reactive. The reactive matter includes toxic substances or pathogen bacteria or related soil particles which stay inside the pipes and make the water harmful for the users [1,6]. To resolve this, disinfectants are added to the water distribution networks. Chlorine (Cl) being the most common disinfectant is used worldwide for the said purpose. However, it entails various limitations, as the Cl reacts with the water in the pipe, called bulk reaction, or reacts with the pipe wall material, called the wall reaction. Due to these reactions, the concentration of Cl in water reduces with time and this phenomenon is termed Cl decay [7]. The concentration of Cl is designed in such a way that it follows the guideline provided by the World Health Organization. LeChevalliar et al. studied the health risks related to contamination intrusion in water networks [2]. Keramat et al. performed numerical analysis for the contamination intrusion due to pressure transients [8]. Darweesh found that there is a negative effect on the water quality when using variable speed pumps for the water supply network [9]. Ponti et al. and Li et al. used evolutionary algorithms and a multi-parameter monitoring system to detect intrusion and its location in distribution networks, respectively [10,11]. Currently, there is a need for validation of the equation of chorine decay rate and the amount of contamination that may spread into the network at a given time duration after it enters the network. Hence, this study was performed to study; the extent of contaminant spread into the water network and the decay rate of contaminant while being in the water network for a designed duration.
2. Research Methodology
2.1. Study Area
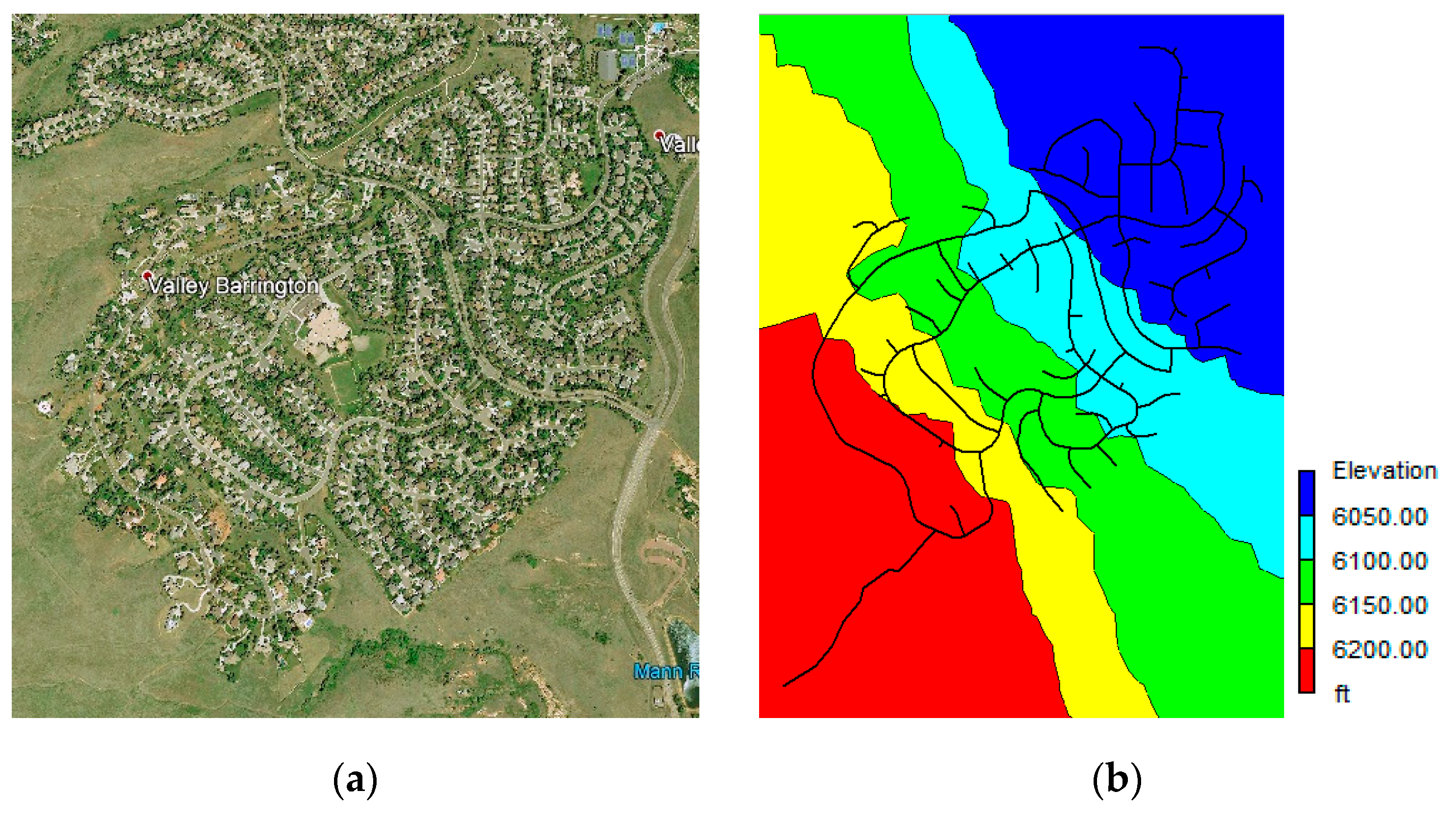
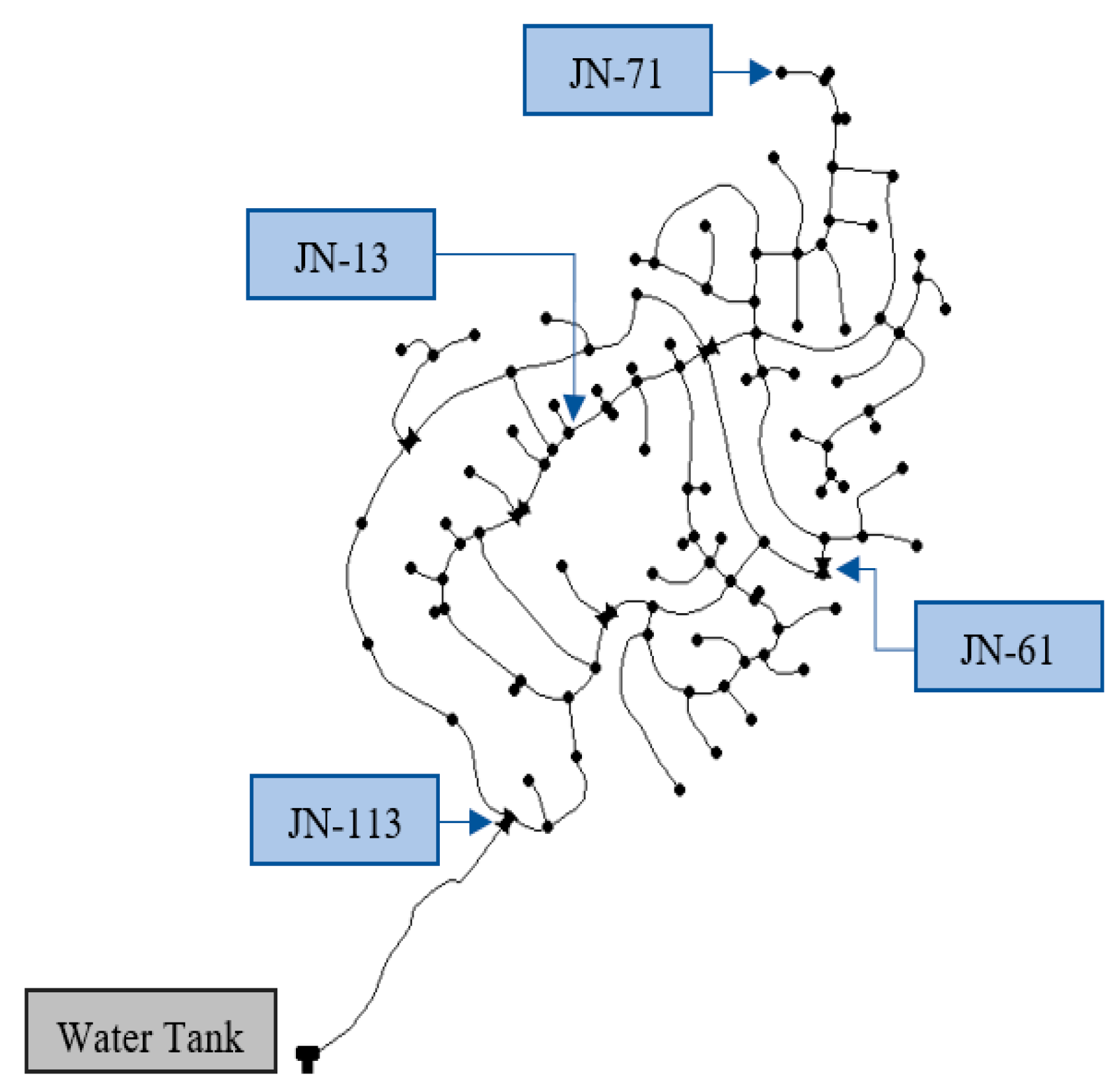
The satellite imagery of the study area is shown in Figure 1a. The valley is a residential area with an approximate population of 3150 and it consists of houses of various sizes including other amenity buildings. The elevation contour plan of the area is shown in Figure 1b. The network model and its all design parameters have been obtained from the website of Aquaveo [12]. The primary source of water for these valleys is the Mann Water Reservoir located on the south-eastern side of the area [12]. The circular water tank (having a diameter of 115 ft (35 m) with a water depth of 10 ft (3 m) is designed to be filled by pumps and the location of the water tank is kept at an elevated area with an elevation of 6320 ft (1925 m) such that the pressure at all joints in the network remains sufficient. The water distribution network (WDN) laid for the area consists of High-Density Poly Ethylene (HDPE) pipe material with a pressure rating of PN-16 (maximum sustainable pressure of 16 bars or 230 psi). The network model in the EPANet 2.2 consists of a total of 116 nodes and 119 pipes. The water distribution pipes range from 3 in. to 6 in. (75 mm to 160 mm) in diameter and the layout used for the simulation is shown in Figure 2.

Figure 1.
(a) Satellite image and (b) elevation contour map of the study area.

Figure 2.
Water supply network for Denver with critical nodes.
2.2. Hydraulic Analysis Parameters
Figure 2 shows the WDN with the location of identified critical nodes that were identified based on their water demand and elevation values. JN-13 was selected for having the highest demand of 7.2 gpm in the network whereas JN-61 was selected for having the lowest demand and no outflow. Also, JN-71 was selected for being the lowest junction in the whole network system with an elevation of 5986 ft (1824 m). The steady-state hydraulic analysis was run by using the Hazen-Williams equation. A roughness coefficient of 150 was used for plastic pipes [13]. The following equation was used for the analysis: , where hL represents the head loss in the pipe, L is the length of the pipe in ft, Q is the volume of water in cfs, C is the Hazen-Williams roughness coefficient, and D represents the diameter of the pipe in ft. The decay of any disinfectant, such as Cl, in WDN, is the function of first-order kinetics as shown in Equation by [14]: , where Ct is the concentration of Cl after a specific duration t, Ci is the initial concentration of Cl, and k is the coefficient of decay.
3. Results and Discussion
3.1. Contaminant Spread
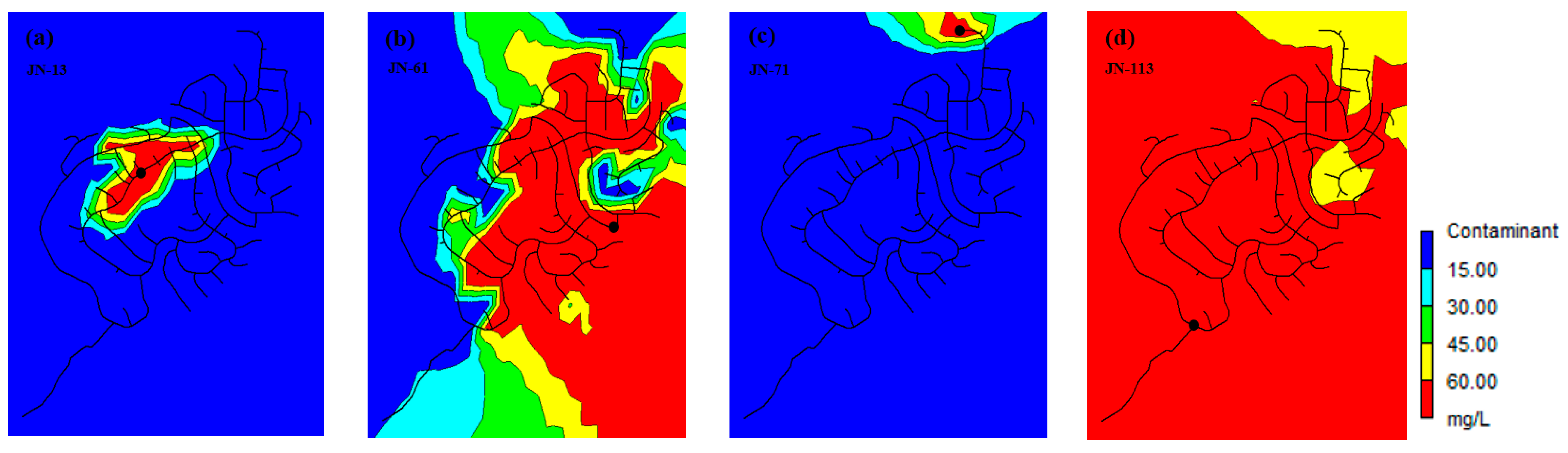
Contour plots of residual Cl were prepared to see the spread of contamination through each node at the end of the design duration and well-justified results were obtained, as shown in Figure 3. The plot obtained from JN-13 having the highest demand shows a very limited spread of the organic material present in the contaminant, which can be compared with the plot obtained for JN-61 having the lowest demand and shows a huge spread of the organic matter. As of JN-61, the contaminant is seen to have traveled even upstream into the network, making it the critical location in the pipe network. Moreover, JN-71, being at the lowest elevation level, shows almost no spread and can be compared to JN-113, being at the highest point in the network and showing the full spread of organic material into the network. If the contaminant enters into a network from the highest point in elevation in the network, the organic matter is likely to spread in the whole network making it the most critical point. The results obtained by the contamination spread plots are justified and validated by obtaining the bulk reaction reports from the EPANet 2.2 program shown in Table 1. The spread percentage of 79.61 shown by the bulk reaction reports indicates that when the contaminant enters at the extreme upstream of the WDN at JN-113, it misbalances almost the whole network and all the downstream pipe junctions are affected.

Figure 3.
Contour plots of contaminant spread at critical nodes shown as dot.

Table 1.
Contaminant spread percentage in the network considered entry at each node.
3.2. Chlorine Decay Rate
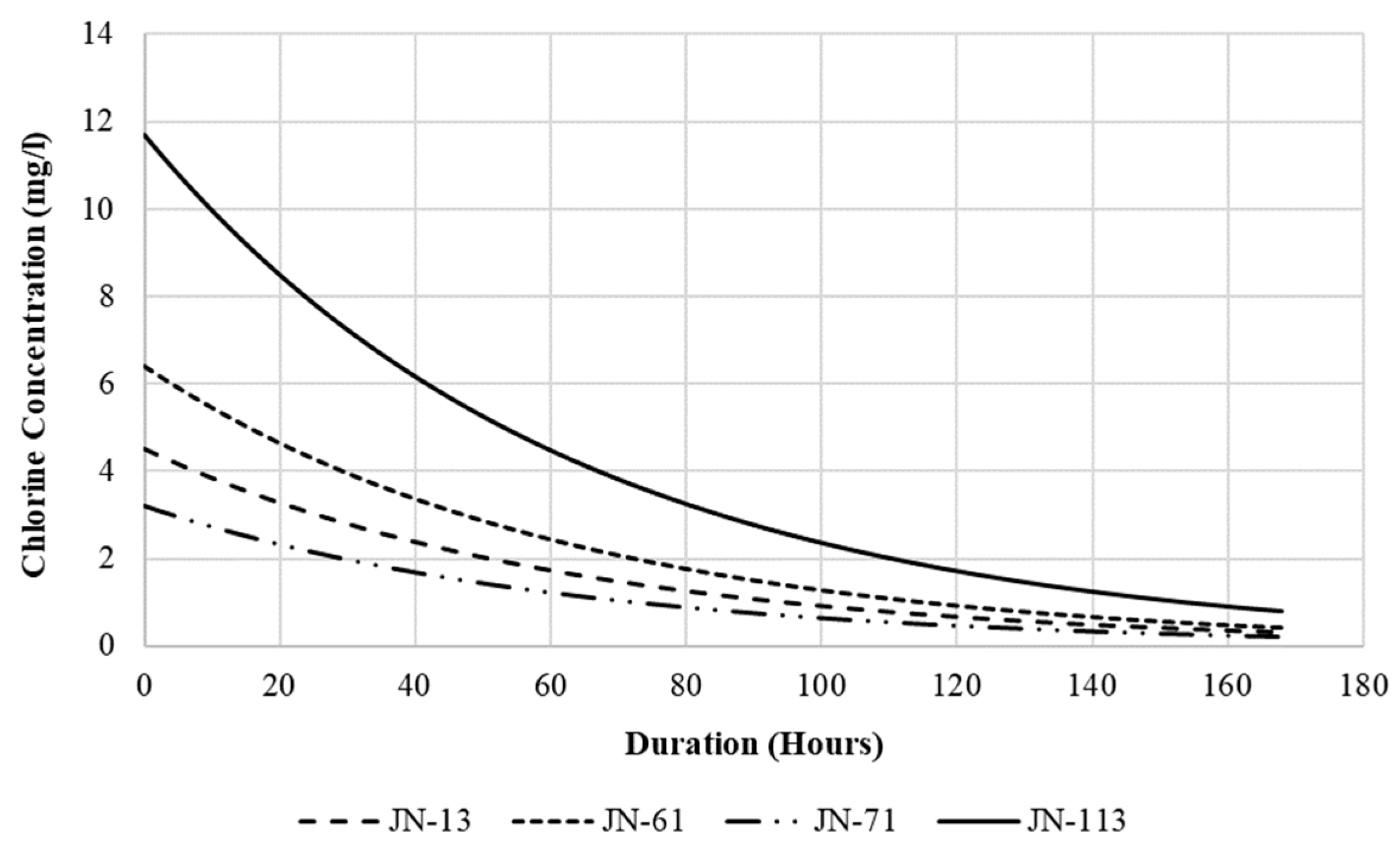
The analysis of Cl decay was performed using the trial and error method. The assumed initial Cl concentration was set in the system and the levels of Cl were monitored for the whole design duration of 168 h. When the level of Cl was found to be above the WHO recommendation at the end of the analysis, the initial concentration was reduced, and the analysis was run again till the values fell within the range. By using the values obtained through simulation, the equation of the trend line for contamination decay at JN-113 was found to be as shown in Figure 4 with an r2 value of 1, .

Figure 4.
Chlorine decay pattern at each node.
The initial Cl concentration at JN-113 was found to be 11.7 mg/L. The coefficient of determination (r2) value for the trend line shows that the data perfectly fit the equation of the line. Similarly, the initial Cl concentrations for JN-13, JN-61, and JN-71 were found to be 4.5 mg/L, 6.4 mg/L, and 3.2 mg/L, respectively. By studying the plots, shown in Figure 4, it was found that the Cl decay rate follows an inverse exponential path for all nodes although the values differ from one node to another.
4. Conclusions
Hydraulic analysis for contamination spread and chlorine decay was performed for a WDN by injecting the contaminant at four identified critical nodes separately. The results of contaminant intrusion analysis present that a contaminant entering at a higher level would spread up to the locations in the network which are lower than the source of contamination. On the other hand, if the contaminant enters the lowest point in the network, it will remain limited to that point and not likely to contaminate the whole system. Also, it was observed that contaminant spread was more at the nodes having lower base demands and such nodes showed more spread of the contaminant. Moreover, it was found that the critical points in the network, responsible for higher contamination spread, need higher initial chlorine concentrations. The chlorine decay rates were found to be the same for all the critical points and the decay rate follows an inverse exponential relation relating to the time. The critical points in a water supply network mentioned in this research can be monitored regularly for any damage or irregularity to avoid any incident of contaminant intrusion. Also, the quality of chlorine to be added to the water can be regularized by using the results of this research. This research can be very useful for the management, planning, and maintenance of water distribution networks.
Author Contributions
Conceptualization, R.J. and H.A.A.; methodology, R.J. and M.F.M.; software, R.J.; validation, H.A.A. and M.F.M.; resources, H.A.A. and M.F.M.; data curation, R.J.; writing—original draft preparation, R.J.; writing—review and editing, H.A.A. and M.F.M.; supervision, H.A.A. and M.F.M.; project administration, H.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analyzed in the research are available from the corresponding author and can be furnished upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boyd, G.R.; Wang, H.; Britton, M.D.; Howie, D.C.; Wood, D.J.; Funk, J.E.; Friedman, M.J. Intrusion within a Simulated Water Distribution System due to Hydraulic Transients I: Volumetric Method and Comparison of Results. J. Environ. Eng. 2004, 130, 774–777. [Google Scholar] [CrossRef]
- LeChevallier, M.W.; Gullick, R.W.; Karim, M.R.; Friedman, M.; Funk, J.E. The Potential for Health Risks from Intrusion of Contaminants into the Distribution System from Pressure Transients. J. Water Health 2003, 1, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; Guo, X.; Yan, X.; Hu, C. Review of Urban Drinking Water Contamination Source Identification Methods. Energies 2023, 16, 705. [Google Scholar] [CrossRef]
- Qasem, A.; Jamil, R. GIS-Based Financial Analysis Model for Integrated Maintenance and Rehabilitation of Underground Pipe Networks. J. Perform. Constr. Facil. 2021, 35, 1–8. [Google Scholar] [CrossRef]
- Rodríguez, J.M.; Galván, X.D.; Ramos, H.M.; Amparo, P.A.L. An overview of leaks and intrusion for different pipe materials and failures. Urban Water J. 2014, 11, 1–10. [Google Scholar] [CrossRef]
- Karim, M.R.; Abbaszadegan, M.; Lechevallier, M. Potential for Pathogen Intrusion during Pressure Transients. J. Am. Water Work. Assoc. 2003, 95, 134–146. [Google Scholar] [CrossRef]
- Tamminen, S.; Ramos, H.; Covas, D. Water Supply System Performance for Different Pipe Materials Part I: Water Quality Analysis. Water Resour. Manag. 2008, 22, 1579–1607. [Google Scholar] [CrossRef]
- Keramat, A.; Payesteh, M.; Brunone, B.; Meniconi, S. Interdependence of flow and pipe characteristics in transient induced contamination intrusion: Numerical Analysis. J. Hydroinform. 2020, 22, 473–490. [Google Scholar] [CrossRef]
- Darweesh, M. Impact of variable speed pumps on water quality in distribution systems. Water SA 2018, 44, 419–427. [Google Scholar] [CrossRef]
- Ponti, A.; Candelieri, A.; Giordani, I.; Archetti, F. Intrusion Detection in Networks by Wasserstein Enabled Many-Objective Evolutionary Algorithms. Mathematics 2023, 11, 2342. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Zhang, C.; Fu, G. Generative adversarial networks for detecting contamination events in water distribution systems using multi-parameter, multi-site water quality monitoring. Environ. Sci. Ecotechnol. 2023, 14, 100231. [Google Scholar] [CrossRef] [PubMed]
- Aquaveo, L.L.C. 2023. Available online: https://www.aquaveo.com/ (accessed on 13 April 2023).
- Jamil, R. Frictional Head Loss Relation between Hazen-Williams and Darcy-Weisbach Equations for Various Water Supply Pipe Materials. Int. J. Water 2019, 13, 333–347. [Google Scholar] [CrossRef]
- Jamil, R. Performance of a New Pipe Material UHMWPE against Disinfectant Decay in Water Distribution Networks. Clean Technol. Environ. Policy 2018, 20, 1287–1296. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).