Seismic Design of Aluminium Structures in the Second Generation of Eurocode 8 †
Abstract
:1. Introduction
2. The Next Eurocode 8
3. Seismic Design of Aluminium Structures According to prEN 1998-1-2
3.1. Generality
3.2. Material Properties
3.3. Structural Types, Ductility Classes, and Behaviour Factors
3.4. Verification to Limit States
3.4.1. Deformation-Related Requirements
- −
- dr,SD ≤ 0.020 hs for moment frames;
- −
- dr,SD ≤ 0.015 hs for frames with concentric bracings, for dual frames, for inverted pendulum structures and for all other structural types.
3.4.2. Design Rules for Dissipative (DC2) Aluminium Structures
- Rd is the resistance of the connection in accordance with prEN 1999-1-1;
- Rfo is the nominal plastic resistance of the connected dissipative element;
- ωrm is the material overstrength factor in the dissipative zones, which is assumed equal to 1.45 unless the National Annex gives a different value for use in a country;
- ωsh is the hardening factor in the dissipative zones, taken as 1.3 or the value calculated in accordance with EN1999-1-1, whichever is greater for elements in plastic bending. For elements in plastic tension it is equal to 1.5 or the ratio , whichever is the greater.
- NEd,G, MEd,G, and VEd,G are the axial force, the bending moment, and shear force in the non-dissipative member due to the non-seismic actions included in the combination of actions for the seismic design situation, respectively;
- NEd,E, MEd,E, and VEd,E are the axial force, the bending moment, and shear force in the non-dissipative member to the design seismic action;
- Ω is the action magnification factor given according to Table 4.
4. Conclusive Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mazzolani, F.M. Aluminium Alloy Structures; Pitman: London, UK, 1985. [Google Scholar]
- Mazzolani, F.M. Aluminium Alloy Structures, 2nd ed.; E&FN Spon: London, UK, 1995. [Google Scholar]
- Mazzolani, F.M. Structural Applications of Aluminium in Civil Engineering. Struct. Eng. Int. 2006, 16, 280–285. [Google Scholar] [CrossRef]
- Skejic, D.; Boko, I.; Toric, N. Aluminium as a material for modern structures. Gradevinar 2015, 67, 1075–1085. [Google Scholar]
- Skejic, D.; Mazzolani, F.; Curkovic, I.; Damjanovic, D. Experimental Testing of Prefabricated Aluminium Knee Joints Reinforced by Steel. In Proceedings of the INALCO2019: 14th International Aluminium Conference, Tokyo, Japan, 13–15 November 2019; pp. 160–161. [Google Scholar]
- Rai, D.C.; Wallace, B.J. Aluminium shear-links for enhanced seismic resistance. Earthq. Eng. Struct. Dyn. 1998, 27, 315–342. [Google Scholar] [CrossRef]
- De Matteis, G.; Brando, G.; Mazzolani, F.M. Hysteretic behaviour of bracing-type pure aluminium shear panels by experimental tests. Earthq. Eng. Struct. Dynam. 2011, 40, 1143–1162. [Google Scholar] [CrossRef]
- Wu, Y.; Peng, L.X.; He, X.C.; Yang, J.S. Experimental and numerical analyses on mechanical properties of aluminum alloy L-shaped joints under cyclic load. Eng. Struct. 2021, 245, 112854. [Google Scholar] [CrossRef]
- De Martino, A.; Landolfo, R.; Mazzolani, F.M. The use of the Ramberg-Osgood law for materials of round-house type. Mater. Struct. 1990, 23, 59–67. [Google Scholar] [CrossRef]
- Mazzolani, F.M.; Cappelli, M.; Spasiano, G. Plastic analysis of aluminium alloy members in bending. Aluminium 1985, 61, 734–741. [Google Scholar]
- Mazzolani, F.M. 3D aluminium structures. Thin-Walled Struct. 2012, 61, 258–266. [Google Scholar] [CrossRef]
- Georgantzia, E.; Gkantou, M.; Kamaris, G.S. Aluminium alloys as structural material: A review of research. Eng. Struct. 2021, 227, 111372. [Google Scholar] [CrossRef]
- Landolfo, R.; Mazzolani, F.M. Different approaches in the design of slender aluminium alloy sections. Thin-Walled Struct. 1997, 27, 85–102. [Google Scholar] [CrossRef]
- Moen, L.A.; De Matteis, G.; Hopperstad, O.S.; Langseth, M.; Landolfo, R.; Mazzolani, F.M. Rotational capacity of aluminum beams under moment gradient. II: Numerical simulations. J. Struct. Eng. 1999, 125, 921–929. [Google Scholar] [CrossRef]
- De Matteis, G.; Moen, L.A.; Langseth, M.; Landolfo, R.; Hopperstad, O.S.; Mazzolani, F.M. Cross-sectional classification for aluminum beams—Parametric study. J. Struct. Eng. 2001, 127, 271–279. [Google Scholar] [CrossRef]
- Manganiello, M.; De Matteis, G.; Landolfo, R. Inelastic flexural strength of aluminium alloys structures. Eng. Struct. 2006, 28, 593–608. [Google Scholar] [CrossRef]
- Zhu, J.H.; Young, B. Tests and design of aluminum alloy compression members. Struct. Eng. 2006, 132, 1096–1107. [Google Scholar] [CrossRef]
- EN1999-1-1; Eurocode 9: Design of Aluminium Structures—Part 1-1: General Structural Rules. CEN: Brussels, Belgium, 2007.
- EN 1998-1; Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. CEN: Brussels, Belgium, 2005.
- Landolfo, R. Assessment of EC8 Provisions for Seismic Design of Steel Structures; Technical Committee 13—Seismic Design, No 131/2013; ECCS: Brussels, Belgium, 2013. [Google Scholar]
- prEN 1998-1-1; 2022, Eurocode 8, Design of Structures for Earthquake Resistance, Part 1-1: General Rules and Seismic Action. CEN/TC 250/SC 8. CEN: Brussels, Belgium, 2022.
- prEN 1998-1-2; 2022, Eurocode 8, Design of Structures for Earthquake Resistance, Part 1-2: General Rules and Seismic Action. CEN/TC 250/SC 8. CEN: Brussels, Belgium, 2022.
- AIJ. Recommendation for Seismic Design of Aluminium Structures; Architectural Institute of Japan: Tokyo, Japan, 2003. (In Japanese) [Google Scholar]
- Hopperstad, O.S.; Langseth, M.; Remseth, S. Cyclic stress-strain behaviour of alloy AA6060, Part I: Uniaxial experiments and modelling. Int. J. Plast. 1995, 11, 725–739. [Google Scholar] [CrossRef]
- Srivatsan, T.S. An investigation of the cyclic fatigue and fracture behavior of aluminum alloy 7055. Mater. Des. 2002, 23, 141–151. [Google Scholar] [CrossRef]
- Borrego, L.P.; Abreu, L.M.; Costa, J.M.; Ferreira, J.M. Analysis of low cycle fatigue in AlMgSi aluminium alloy. An. Mec. Fract. 2003, 20, 179–184. [Google Scholar] [CrossRef]
- Yahya, M.M.; Mallik, N.; Chakrabarty, I. Low cycle fatigue (LCF) behaviour of AA6063 aluminium alloy at room temperature. Int. J. Emerg. Technol. Adv. Eng. 2015, 5, 100. [Google Scholar]
- Dusicka, P.; Tinker, J. Global restraint in ultra-lightweight buckling-restrained braces. J. Compos. Construct. 2013, 17, 139–150. [Google Scholar] [CrossRef]
- Pisapia, A.; Nastri, E.; Piluso, V.; Formisano, A.; Mazzolani, F.M. Experimental campaign on structural aluminium alloys under monotonic and cyclic loading. Eng. Struct. 2023, 282, 115836. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Di Lorenzo, G.; De Martino, A. Influence of EC8 rules on p-delta effects on the Design and response of steel MRF. Ing. Sismica 2018, 35, 104–120. [Google Scholar]
- Tartaglia, R.; D’Aniello, M.; Landolfo, R. Seismic performance of Eurocode-compliant ductile steel MRFs. Earthq. Eng. Struct. Dyn. 2022, 51, 2527–2552. [Google Scholar] [CrossRef]
- Marino, E.M. A unified approach for the design of high ductility steel frames with concentric braces in the framework of Eurocode 8. Earthq. Eng. Struct. Dyn. 2013, 43, 97–118. [Google Scholar] [CrossRef]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Seismic design criteria for chevron CBFs: Proposals for the next EC8 (PART-2). J. Construct. Steel Res. 2017, 138C, 17–37. [Google Scholar] [CrossRef]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Proposal of design rules for ductile X-CBFS in the framework of EUROCODE 8. Earthq. Eng. Struct. Dyn. 2018, 48, 124–151. [Google Scholar] [CrossRef]
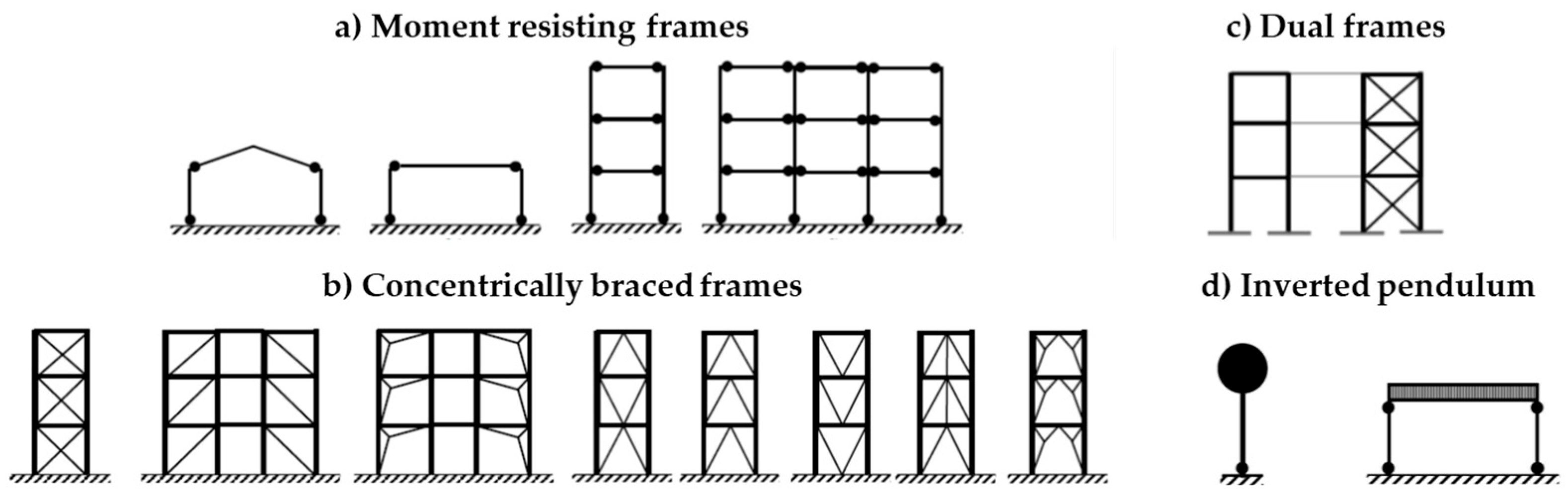
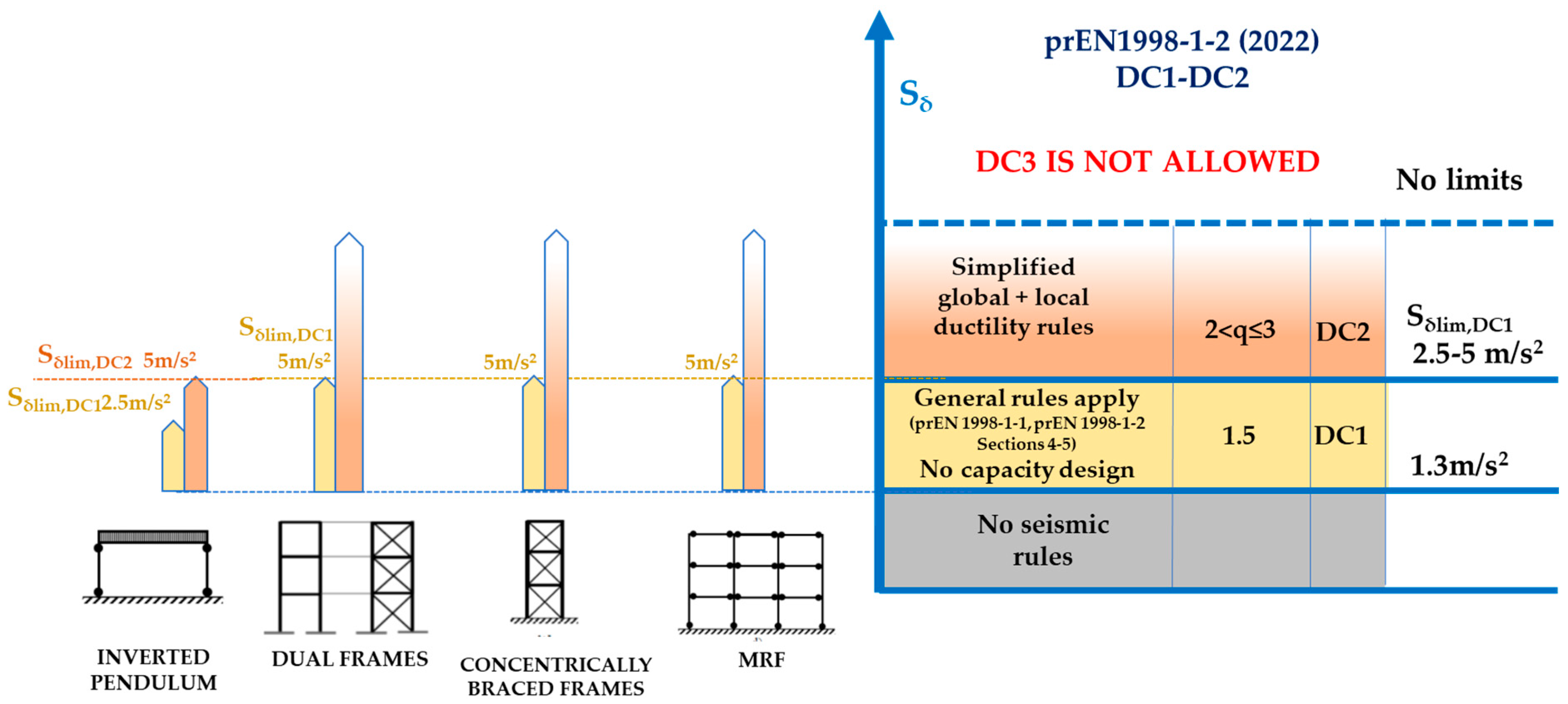
| Seismic Action Class | Reference Spectral Accel. Sα,475 | Seismic Action Index Sδ |
|---|---|---|
| High | Sα,475 ≥ 5.0 m/s2 | Sδ ≥ 6.50 m/s2 |
| Moderate | 2.5 m/s2 ≤ Sα,475< 5.0 m/s2 | 3.25 m/s2 ≤ Sδ < 6.50 m/s2 |
| Low | 1.0 m/s2 ≤ Sα,475 < 2.5 m/s2 | 1.30 m/s2 ≤ Sδ < 3.25 m/s2 |
| Very low | Sα,475 < 1.0 m/s2 | Sδ < 1.30 m/s2 |
| Structural Element | Product Form | Alloy | Temper | Thickness |
|---|---|---|---|---|
| Sheet, strip, and plate | _ | 5052 | H12|H22/H32 | ≤40 |
| 5049 | O/H111 | ≤100 | ||
| 5083 | O/H111 | ≤80 | ||
| 5383 | O/H111 | ≤120 | ||
| H116/H321 | ≤80 | |||
| 5454 | O/H111 | ≤80 | ||
| 5754 | O/H111 | ≤100 | ||
| 6061 | T4/T451 | ≤12.5 | ||
| 6082 | T4/T451 | ≤12.5 | ||
| Extruded profiles, extruded tube, extruded rod/bar, and drawn tube | ET, EP, ER/B | 5083 | O/H111 F/H112 | ≤200 |
| ET, EP, ER/B | 5454 | O/H111 F/H112 | ≤25 | |
| ET, EP, ER/B | 5754 | O/H111 F/H112 | ≤25 | |
| DT | 6060 | T6 | ≤20 | |
| EP, ET, ER/B | T64 | ≤15 | ||
| EP, ET, ER/B | 6061 | T4 | ≤25 | |
| DT | T4 | ≤20 | ||
| EP, ET, ER/B | 6082 | T4 | ≤25 | |
| Legend: EP—Extruded profiles ER/B—Extruded rod and bar | ET—Extruded tube DT—Drawn tube | |||
| Structural Type | DC2 | ||
|---|---|---|---|
| qD | qR | q | |
| Moment-resisting frames (MRFs) | |||
| Single-storey MRFs | 1.5 | 1.1 | 2.5 |
| Multi-storey MRFs | 1.5 | 1.3 | 3.0 |
| Frames with concentric bracings | 1.5 | 1.0 | 2.3 |
| Diagonal bracings | |||
| V-bracings | |||
| X-bracings on either single- or two-storey | |||
| Dual frames (MRFs with concentric bracing) | 1.7 | 1.2 | 3.0 |
| Inverted pendulum | 1.3 | 1.0 | 2.0 |
| STRUCTURAL TYPE | Ω | Members to Which (Equation (4)) Apply |
|---|---|---|
| Moment-resisting frames (MRFs) | ||
| Single-storey MRFs | 1.8 | columns |
| Multi-storey MRFs | 2.0 | |
| Frames with concentric bracings | 1.5 | |
| Diagonal bracings | beams and columns | |
| V-bracings | ||
| X-bracings on either single or two-storey | ||
| Dual frames (MRFs with concentric bracing) | 2.0 | beams and columns of the concentric bracing; columns of the MRF |
| Inverted pendulum | 1.5 | columns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landolfo, R.; Mazzolani, F.M. Seismic Design of Aluminium Structures in the Second Generation of Eurocode 8. Eng. Proc. 2023, 43, 12. https://doi.org/10.3390/engproc2023043012
Landolfo R, Mazzolani FM. Seismic Design of Aluminium Structures in the Second Generation of Eurocode 8. Engineering Proceedings. 2023; 43(1):12. https://doi.org/10.3390/engproc2023043012
Chicago/Turabian StyleLandolfo, Raffaele, and Federico Massimo Mazzolani. 2023. "Seismic Design of Aluminium Structures in the Second Generation of Eurocode 8" Engineering Proceedings 43, no. 1: 12. https://doi.org/10.3390/engproc2023043012
APA StyleLandolfo, R., & Mazzolani, F. M. (2023). Seismic Design of Aluminium Structures in the Second Generation of Eurocode 8. Engineering Proceedings, 43(1), 12. https://doi.org/10.3390/engproc2023043012







