Abstract
Environmental demands around the world have led to an increasing interest in natural gas due to its advantages over other hydrocarbons used in power generation, which has led to the search for the best way to solve the transportation problem associated with this resource. In this paper, we propose a methodology that allows us to address the non-convexity related to the Weymouth equation that makes the optimization problem so difficult. The mentioned equation, in charge of relating the flows through the pipelines and the pressures at the nodes, is characterized by having a discontinuity in the form of a sign function. The proposal of this work is based on the use of Mathematical Programs with Complementarity Constraints (MPCC) to achieve a good approximation since it allows make certain continuous variables to behave as discrete variables in such a way that it is possible to avoid having to pose a mixed integer programming problem and this one. This approach showed a smaller approximation error (or at least equal) with other approximations used in the state of the art when tested in three different networks: one of 8 nodes, one of 48 nodes tested in other related works, and one of 63 nodes representing the Colombian natural gas transportation system.
1. Introduction
Natural gas, as an energy source, has achieved great relevance worldwide in recent years due to two fundamental causes: Firstly, it allows reliable supply and continuous development supporting economic growth, which is highly related to energy consumption [1]. Secondly, the low greenhouse gas emission of natural gas makes it attractive for environmental care and sustainable development.
According to a study from 2020, the global demand for natural gas was 1788 billion cubic meters (bcm) in the same year, and the 2040 projection reached 2142 bcm, despite the new regulations for consumption decrease in Europe and the Middle East [2]. Particularly for Latin American countries, constituting the largest consumers of domestic natural gas, the statistics rise from 96 bcm in 2020 to 148 bcm in 2040. For most above countries, natural gas must also counteract the reduction of hydroelectric generation during dry seasons while supplying residential, commercial, and industrial demands [3]. Hence, there is a need for natural gas systems that fully supply all kinds of demand at a minimal fuel.
In general, natural gas systems are composed of four fundamental elements: injection fields (or re-gasification plants), providing the fuel at regulated pressure; gas pipelines, transporting the gas from sender to receiver nodes; compressors, raising the input-to-output pressure; and end users, establishing the fuel demand. Several authors have proposed different ways to model the above elements and their interconnections, thus supplying the demand through optimization techniques [4]. Though the extensive work on each element, the gas pipelines remain a rather complex modeling problem since the physical relationship between the pressures at its ends and the flow through it, known as the Weymouth equation, holds a sign function determining the flow direction. As a nonconvex and discontinuous equality constraint, such a function poses a strong challenge in optimization [5].
The challenge imposed by the Weymouth equation promoted the development of optimization approaches with mathematical complexities without compromising the computational cost [6]. The first family of approaches turned the signum function into a linear combination with binary auxiliary variables yielding a mixed integer optimization problem [7]. Despite integrating discontinuities, mixed integer optimization problems present a significant source of nonconvexities reducing the probability of reaching a global optimum [8]. Further, the computational complexity of mixed integer programming is considerably larger than other optimization approaches [9]. As another solution, optimization through heuristic algorithms straightforwardly deals with nonlinear constraints [10]. However, their high sensitivity to initial conditions leads to suboptimal solutions [9]. Linearization and convexification strategies relax the Weymouth constraint reducing the computational complexity [11]. For instance, the binary auxiliary variables weigh piecewise linear functions that approximate the nonlinearities [12]. Another linear approximation relies on the Taylor series to replace nonlinear equations with a series of linear inequalities [13]. As an example of relaxation through convexification, the Second-order cone (SOC) programming introduces continuous and binary auxiliary variables and guarantees a global optimum on the approximation [14]. More recently, a polynomial regression holding odd coefficients approximates the Weymouth equation, its first and second derivative at the ends of a predefined operating interval [15]. Despite the reduced complexity and compatibility with conventional solvers, previous strategies result in Weymouth approximations that infringe on physical pipeline behavior, some of them to a great extent.
For reducing approximation errors, this work formulates the Weymouth equation in terms of mathematical programming with complementarity constraints (MPCC) that, instead of imposing an equality constraint, solves an optimization problem. MPCC expresses the signum function as an optimization problem with linearly constrained continuous variables behaving as binary, with two advantages: Firstly, the gas transport optimization avoids solving a complex mixed integer problem [16]. Secondly, MPCC not only constrains the original problem, but also minimizes the Weymouth approximation error.
The paper agenda is as follows: Section 2 describes both the objective function and constraints in the optimization problem. Section 3 proposes the problem solution using MPCC for modeling the Weymouth equation. Section 4 compares proposed MPCC against three Weymouth approximation approaches for 8-node, 48-node, and 63-node networks, the latter a case study of the Colombian gas transportation system. Finally, Section 5 concludes with the main findings and proposes future work.
2. Problem Formulation for Natural Gas Transport
The natural gas transmission network can be represented as a directed graph , where the set of vertices corresponds to the system nodes. The nodes with gas injection are known as wells, denoted by , with an associated gas flow . The nodes demanding gas are known as users, , holding an individual cost for diversified loads. Due to the operational rationing scenarios, this study considers a virtual flow at each user accounting for the unsupplied gas demand. For simplicity, nodes cannot be wells and users simultaneously, i.e., . The set of directed edges connect node pairs through two kinds of transmission elements, pipelines , and compressing stations . Note that edges must necessarily correspond to either a pipeline or a compressor, that is, . Since gas pipelines admit bidirectional flow , the edge direction is arbitrarily chosen, being positive when flowing in the chosen direction and negative otherwise. For gas flow through compressors , the values must always be positive, as bi-directional stations are not considered.
Since the objective of natural gas transport is supplying the user’s demand at the lowest cost, the optimization problem in Equation (1) takes place by including the following operation costs: for injecting gas into the system by production wells, for pipeline transportation, for pressure boosting by compressing stations, and for unsupplied demand penalties. The set gathers all flows as decision variables for the optimization problem. Hence, each term in the summation becomes a function of the number of natural gas units used in its respective element.
To mathematically model the technical limits and the physical behavior, the optimization problem objective function considers the following constraints: Equation (2) limits the flow injected by the production wells to its technical maximum/minimum injection capacity /. Equation (3) truncates the pipeline capacity at the structural maximum and allows bidirectional flows. Equation (4) considers the maximum compression through the output-to-input pressure ratio , resulting in a linear inequality constraint. and technically bound node pressures in Equation (5). Regarding the rationing, Equation (6) limits the unsupplied demand between the desired zero and the respective user demand . Finally, two equalities guarantee the physical behavior of the gas in the system. Equation (7), termed nodal gas balance, linearly matches each node’s injected with ejected gas. The Weymouth equality in Equation (8) ties the pressure at two nodes with the flow through the pipeline connecting them using a structural constant . Particularly, the Weymouth constraint is nonlinear, nonconvex, and disjunctive due to the sign function.
3. Problem Solution Using Complementarity Constraints for Nonconvex Functions
The sign function in Section 2 poses a challenge for conventional optimization approaches due to its non-derivability, non-linearity, and nonconvexity. This work proposes to deal with such a challenge using the mathematical technique of Mathematical Programs with Complementarity Constraints (MPCC). Complementarity refers to a relationship between variables where one or both must be at their bound, modeling mutually exclusive situations without the need for binary variables. Here, MPCC turns the discontinuous sign function into bounded continuous variables resulting from the optimization problem with the complementarity constraints in Equations (9) to (14). The Equations (9) to (14) indicate that when is positive, will be positive and equal in magnitude to , while would necessarily be zero. Otherwise, when is negative, it will be that takes the value in magnitude of the transport flow of interest and that adjusts its value to zero. The Equation (14), in either of the two cases above, guarantees that the variable y takes the value of 1 if the sign of is positive or if the sign of is negative. Note that the proposed solution avoids the formulation of conventional mixed integer optimization approaches [17].
To solve the resulting optimization problem, we resorted to the IPOPT solver, which is characterized by its use of a Primal-Dual Barrier Approach. This method works by converting the model into an unconstrained optimization problem, using a barrier function to penalize solutions that do not satisfy the constraints of the original problem. This algorithm allows convergence starting from poor initial points and incorporates a line-search filter, an important feature that helps to ensure progress towards a solution at each step by using the Armijo condition as a criterion. This condition requires that the objective function decreases by a sufficient amount relative to the step length. If the step is not sufficiently successful, the line-search filter reduces the step length and the algorithm takes a smaller step [18]. The main feature of this algorithm is that it finds the solution to the problem by moving through the feasible solution region using a central path [19]. Additionaly this solver incorporates a variation of the original algorithm that solves both the primal and dual problems, which has shown superior performance compared to the standard version of the algorithm in practice [20].
4. Case Study
This work tests the efficiency of the proposed approach in three cases: A small system with one closed trajectory, a 48-node system with several closed trajectories, and a 63-node system representing the Colombian natural gas system. All cases were tested in Google Colab notebooks using the Gekko optimization tool [21] to implement the internal complementarity constraints for the sign function.
To validate the performance of the solution obtained by the proposed approach, it was compared with three approaches used in the state of the art to solve this same problem: replacing the equality constraint with a series of linear inequalities using the Taylor Series method [13], convexifying the problem using second-order cone programming (SOC) [14] and approximating the equation in a defined interval using a polynomial of degree five with odd coefficients only [15].
To compare the proposal presented in this study with other approximations, it was decided to take the solution obtained with each solver and evaluate it in the Weymouth equation equated to zero, so quantifying the approximation error.
4.1. 8-Node Natural Gas System
In the first instance, an 8-node database (Figure 1) was used for the study for two main reasons. The first is that being a small network, it presented an additional facility when corroborating the results. Despite the above, this network had a closed trajectory, an additional difficulty since it required the use of bidirectional pipelines, making it a very good starting point for the different approaches used.
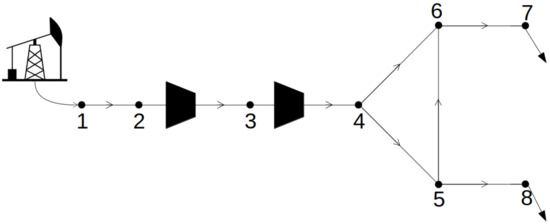
Figure 1.
8-node natural gas system.
The optimization problem was solved using each of the four approaches. None of the results obtained had to reach the point of rationing the hydrocarbon and, as shown in the Table 1, in three of them the result of the objective function was the same. Apart from the value of the objective function, which represents the operating cost of the system, in this study, it is of interest to know how good the solutions achieved with each of the approaches are. To understand it better, it can be seen that each of the pipelines has an associated equation of form Equation (8), so if the respective pressures and flows of these elements obtained when the problem was solved are taken, each Weymouth equation can be evaluated in order to quantify the amount of error in the approximation.

Table 1.
Value of the objective function using each approach in each system.
The boxplots in Figure 2 contain the resulting values when the solution obtained by each of the respective approximations was evaluated in the equation equal to zero, i.e., the value to which it should ideally tend. Here a paired test yielded that the MPCC approximation gave the smallest error.
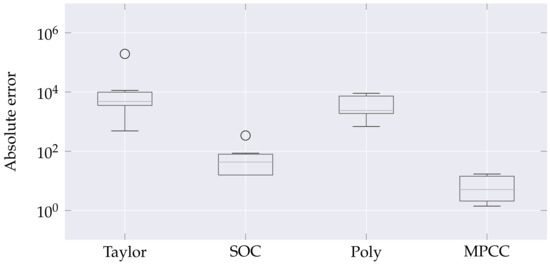
Figure 2.
Absolute approximation error in Weymouth equation for the 8 nodes network. The boxplots illustrate the error dispersion for each considered approach. The whiskers bound the error first and third quartiles, and the circles denote outlying approximation errors.
4.2. 48-Node Natural Gas System
The second tested case is the 48-node database used by [22], among other authors in state of the art. This network, which can be seen in Figure 3, is composed of 9 injection fields, 8 compressor stations, and 22 gas demand nodes. This system was selected since its structure has several loops, which represent an additional difficulty in the solution of the problem and therefore it is a good way to test the robustness of the tested models.
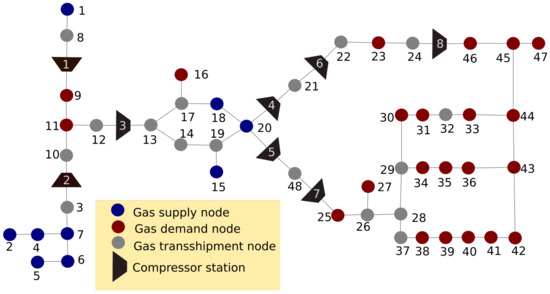
Figure 3.
48-node natural gas system [23].
Unlike the previous system, in this case, all approaches performed quite similarly in terms of the value of the objective function. Table 1 shows how the difference between approaches was practically negligible. Despite the above, this behavior was not maintained in the results obtained when the errors of the approaches were compared. As seen in Figure 4, the approximation using the Taylor series presented the highest error, followed by the polynomial approximation. In this case, the error presented by the Taylor series and MPCC was quite similar, being a statistical test the one that determined that the latter approach had a significantly lower error.
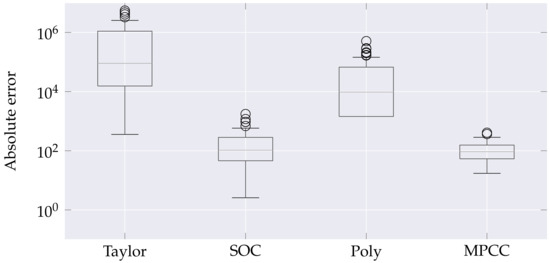
Figure 4.
Absolute approximation error in Weymouth equation for the 48 nodes network. The boxplots illustrate the error dispersion for each considered approach. The whiskers bound the error first and third quartiles, and the circles denote outlying approximation errors.
In this case, it is necessary to highlight the increase in error values with respect to those obtained in the 8-node network due to the difference between the systems. The fact of not only having many more elements but also connecting them in more complex configurations is a sample of how the difficulty of this type of optimization problem has quite a high scalability, forcing it to have sufficiently robust models for its solution.
4.3. 63-Node Natural Gas System
The third network corresponds to the Colombian natural gas injection and transportation system illustrated in Figure 5. This system is composed of 13 injection fields, 14 compressor stations, and 26 consumer nodes. Despite being radial, this system considers gas pipelines with bidirectional flows since the change of gas demanded throughout the year is related to the country’s meteorology. For this case, the system introduced in [15] was updated in the Atlantic coast region by grouping elements and fixing the new operational constraints. These changes resulted in a new system with a total of 63 nodes.
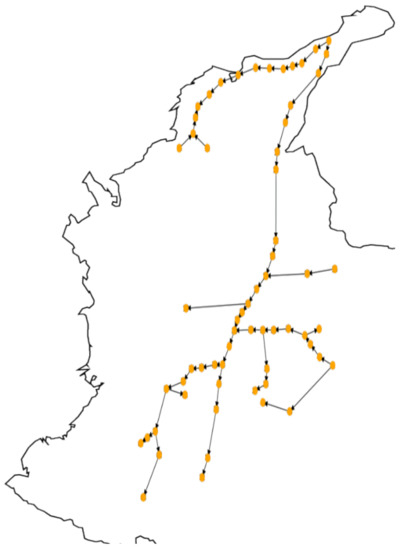
Figure 5.
63-node natural gas system (Colombian system).
Figure 6 presents the absolute errors in approximating the Weymouth equation for the 63-node system. The first observation from the results is that the polynomial approach fails to converge, probably because the optimal flows and pressures fall outside the Weymouth approximation interval. Secondly, the errors for this system are lower than those for the previous one, mainly due to lacking closed trajectories that alleviate the complexity. In terms of performance, despite reaching a cost function value about 4% more expensive, the proposed MPCC-based solution significantly decreases the error on the Weymouth approximation compared to Taylor and SOC. Lastly, it is worth noting that MPCC yields two outlier errors, almost five orders larger than the average. After a manual exploration, we found the same outlying errors in Taylor and SOC at two pipelines between compressors. We hypothesize that the pressures at the ends and the flow through the pipe are over-constrained, so the solvers only accomplish the linear relationships of compressing ratios and gas balance instead of the complex Weymouth equation. Therefore, the MPCC-based solution provides more realistic gas transportation solutions due to a systematical reduction of Weymouth approximation errors.
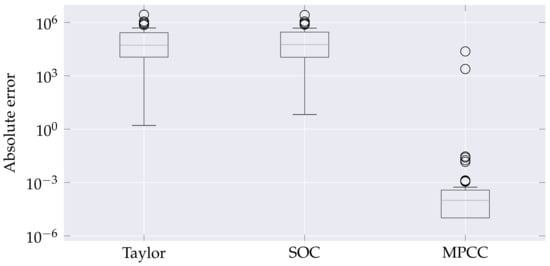
Figure 6.
Absolute approximation error in Weymouth equation for the Colombian network. The boxplots illustrate the error dispersion for each considered approach. The whiskers bound the error first and third quartiles, and the circles denote outlying approximation errors.
5. Concluding Remarks and Future Work
This work proposed a solution for dealing with the Weymouth equation within the framework of natural gas transportation through complementarity constraints. MPCC formulated the nonconvex signum function in the Weymouth equation in terms of continuous bounded variables instead of binary ones, avoiding mixed integer programming. The proposed solution was contrasted against Taylor series, SOC, and polynomial approaches regarding the absolute approximation error at three study cases: An 8-node network with one closed trajectory, a 48-node network with multiple closed trajectories, and a 63-node radial network representing the Colombian gas transportation system. For experimental integrity, the IPOPT library solved all programming problems for all contrasted approaches. Experimental results evidenced that the proposed MPCC solution attained an approximation error smaller than contrasted approaches. Therefore, approximating the Weymouth equation using MPCC yielded pressures and flows satisfying the technical limits and physical behavior demanded by natural gas transportation problems.
For future work, we devise the following research directions. Firstly, the problem formulation will be extended to stochastic programming for natural gas transportation scenarios without a deterministic demand. Such scenarios are common for power generation that relies heavily on hydroelectric inputs and thermal power plants to fulfill the remaining demand. Secondly, a study of potential expansion plans must be conducted by evaluating various investment options in a robust and reliable solution for gas optimization problems.
Author Contributions
Data Extraction, Á.A.O.-G. and M.H.-L.; Validation, D.A.C.-P., and A.M.Á.-M.; Original Draft Preparation, C.A.B.-M., Á.A.O.-G., and D.A.C.-P.; Review and Editing, C.A.B.-M., and D.A.C.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Minciencias project: “Desarrollo de una herramienta para la planeación a largo plazo de la operación del sistema de transporte de gas natural de Colombia”—código de registro 69982—CONVOCATORIA DE PROYECTOS CONECTANDO CONOCIMIENTO 2019 852-2019.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Thanks to the Maestría en Ingeniería Eléctrica, graduate program of the Universidad Tecnológica de Pereira.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alam, M.S.; Paramati, S.R.; Shahbaz, M.; Bhattacharya, M. Natural gas, trade and sustainable growth: Empirical evidence from the top gas consumers of the developing world. Appl. Econ. 2017, 49, 635–649. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Restrepo-Trujillo, J.; Moreno-Chuquen, R.; Jiménez-García, F.N. Strategies of expansion for Electric Power Systems based on hydroelectric plants in the context of climate change: Case of analysis of Colombia. Int. J. Energy Econ. Policy 2020, 10, 66–74. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Shahidehpour, M. Robust Co-Optimization Scheduling of Electricity and Natural Gas Systems via ADMM. IEEE Trans. Sustain. Energy 2017, 8, 658–670. [Google Scholar] [CrossRef]
- Liu, F.; Bie, Z.; Wang, X. Day-ahead dispatch of integrated electricity and natural gas system considering reserve scheduling and renewable uncertainties. IEEE Trans. Sustain. Energy 2019, 10, 646–658. [Google Scholar] [CrossRef]
- Yao, L.; Wang, X.; Ding, T.; Wang, Y.; Wu, X.; Liu, J. Stochastic day-ahead scheduling of integrated energy distribution network with identifying redundant gas network constraints. IEEE Trans. Smart Grid 2019, 10, 4309–4322. [Google Scholar] [CrossRef]
- Üster, H.; Dilaveroğlu, Ş. Optimization for design and operation of Natural Gas Transmission Networks. Appl. Energy 2014, 133, 56–69. [Google Scholar] [CrossRef]
- Klatzer, T.; Bachhiesl, U.; Wogrin, S. State-of-the-art expansion planning of integrated power, natural gas, and Hydrogen Systems. Int. J. Hydrogen Energy 2022, 47, 20585–20603. [Google Scholar] [CrossRef]
- Raheli, E.; Wu, Q.; Zhang, M.; Wen, C. Optimal coordinated operation of Integrated Natural Gas and Electric Power Systems: A review of modeling and solution methods. Renew. Sustain. Energy Rev. 2021, 145, 111134. [Google Scholar] [CrossRef]
- He, C.; Zhang, X.; Liu, T.; Wu, L.; Shahidehpour, M. Coordination of interdependent electricity grid and natural gas network—A review. Curr. Sustain. Energy Rep. 2018, 5, 23–36. [Google Scholar] [CrossRef]
- Singh, M.K.; Kekatos, V. Natural gas flow solvers using convex relaxation. IEEE Trans. Control Netw. Syst. 2020, 7, 1283–1295. [Google Scholar] [CrossRef]
- Correa-Posada, C.M.; Sánchez-Martín, P. Gas Network Optimization: A comparison of Piecewise Linear Models. Optimization Online. 2014, pp. 1–24. Available online: https://optimization-online.org/2014/10/4580/ (accessed on 5 May 2022).
- Fodstad, M.; Midthun, K.T.; Tomasgard, A. Adding flexibility in a natural gas transportation network using interruptible transportation services. Eur. J. Oper. Res. 2015, 243, 647–657. [Google Scholar] [CrossRef]
- Schwele, A.; Ordoudis, C.; Kazempour, J.; Pinson, P. Coordination of Power and Natural Gas Systems: Convexification Approaches for Linepack Modeling. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- García-Marín, S.; González-Vanegas, W.; Murillo-Sánchez, C. MPNG: A MATPOWER-Based Tool for Optimal Power and Natural Gas Flow Analyses. IEEE Trans. Power Syst. 2022, 1–9. [Google Scholar] [CrossRef]
- Baumrucker, B.; Biegler, L. MPEC strategies for cost optimization of Pipeline Operations. Comput. Chem. Eng. 2010, 34, 900–913. [Google Scholar] [CrossRef]
- Baumrucker, B.; Renfro, J.; Biegler, L. MPEC problem formulations and solution strategies with chemical engineering applications. Comput. Chem. Eng. 2008, 32, 2903–2913. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2005, 106, 25–57. [Google Scholar] [CrossRef]
- Nemirovski, A.S.; Todd, M.J. Interior-point methods for optimization. Acta Numer. 2008, 17, 191–234. [Google Scholar] [CrossRef]
- Dahl, J.; Andersen, E.D. A primal-dual interior-point algorithm for nonsymmetric exponential-cone optimization. Math. Program. 2021, 194, 341–370. [Google Scholar] [CrossRef]
- Beal, L.D.R.; Hill, D.C.; Martin, R.A.; Hedengren, J.D. GEKKO Optimization Suite. Processes 2018, 6, 106. [Google Scholar] [CrossRef]
- Chen, S.; Conejo, A.J.; Sioshansi, R.; Wei, Z. Unit Commitment With an Enhanced Natural Gas-Flow Model. IEEE Trans. Power Syst. 2019, 34, 3729–3738. [Google Scholar] [CrossRef]
- García-Marín, S.; González-Vanegas, W.; Murillo-Sánchez, C.E. MATPOWER/mpng: MPNG. 2019. Available online: https://github.com/MATPOWER/mpng (accessed on 17 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).