Automata Based Multivariate Time Series Analysis for Anomaly Detection over Sliding Time Windows †
Abstract
1. Introduction
- Symbolically describe abnormal behaviours through patterns;
- Find the occurrences of these patterns in the time series;
- Identify the occurrences of those patterns whose numerical characteristics are deviant.
2. Background on Multivariate Time Series
2.1. Alphabet as a Mean to Describe Conditions between Adjacent Measures
2.2. Signature of the Multivariate Time Series
2.3. Pattern and Feature as Qualitative and Quantitative Aspects of Anomalies
2.4. Seed Transducers
 and
and 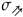 , respectively, corresponding to and , where
, respectively, corresponding to and , where  describes a simultaneous decrease in both temperature and humidity, and
describes a simultaneous decrease in both temperature and humidity, and 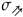 an increase. Figure 1A shows two maximal occurrences of
an increase. Figure 1A shows two maximal occurrences of 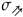 in the multivariate time series . Using the feature, we obtain and as the lengths of the two occurrences. Using the sumaggregator, we obtain a total length . These values are computed using the transducer given in Figure 1B, which describes the transitions from the initial state s.
in the multivariate time series . Using the feature, we obtain and as the lengths of the two occurrences. Using the sumaggregator, we obtain a total length . These values are computed using the transducer given in Figure 1B, which describes the transitions from the initial state s.3. Optimal Patterns Extraction from Sliding Windows
3.1. Register-Based Features Evaluation on a Time Series
- R gradually records the sum of the feature values of f on each completely terminated found occurrence of (i.e., );
- C stores the feature value of the current occurrence for which we did not yet reach the end (i.e., );
- D contains the feature value of the current potential part of an occurrence ().
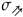 is 1. Similarly, means that we obtain a potential extra part of the already found occurrence of
is 1. Similarly, means that we obtain a potential extra part of the already found occurrence of 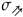 . We then compute its length with . means that we are still inside an occurrence of
. We then compute its length with . means that we are still inside an occurrence of 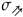 . It then confirms the membership of the encountered extra parts. Thus, we compute . Finally, means that we are no longer in an occurrence of
. It then confirms the membership of the encountered extra parts. Thus, we compute . Finally, means that we are no longer in an occurrence of 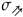 . We then compute to integrate in .
. We then compute to integrate in .3.2. Register-Based Features Evaluation on Sliding Windows
- Computing the Contribution of on a Sliding Window
- Pattern Occurrences Checker in Slidings Windows
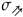 in the multivariate time series of Example 1.
in the multivariate time series of Example 1.- Computing the End of the Next Pattern Occurrence from the Pattern Transducer
- -
- When founde , is updated according to lines 3–9 of Algorithm 1;
- -
- When found , is updated according to lines 10–20 of Algorithm 1.
| Algorithm 1: Computing the end of the next occurrence of pattern for each position. |
 |
4. Anomaly Detection Tool
4.1. Parameters
- The minimum difference threshold is used to determine the minimum variation for two consecutive measures to be considered as different.
- The occupation percentage threshold is the minimum percentage of the window occupation by the pattern wrt its contribution within the window. Thus, an anomaly is detected when the occupation percentage exceeds .
4.2. Experiments
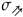 and
and  . The analysis of the results shown in Figure 3 then allows us to conclude that our tool allows one to efficiently identify anomalies occurrences in windows. The addition of parameters and , and the possibility of choosing the pattern to identify makes it possible to characterise the anomalies and to adjust their detection in a better way.
. The analysis of the results shown in Figure 3 then allows us to conclude that our tool allows one to efficiently identify anomalies occurrences in windows. The addition of parameters and , and the possibility of choosing the pattern to identify makes it possible to characterise the anomalies and to adjust their detection in a better way.- Effects of Variation
- Effects of m and Variation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Audibert, J. Unsupervised Anomaly Detection in Time-Series. (Détection Non Supervisée des Anomalies Dans Les Séries Temporelles). Ph.D Thesis, Sorbonne University, Paris, France, 2021. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Beldiceanu, N.; Carlsson, M.; Douence, R.; Simonis, H. Using finite transducers for describing and synthesising structural time-series constraints. Constraints 2016, 21, 22–40. [Google Scholar] [CrossRef]
- Beldiceanu, N.; Carlsson, M.; Quimper, C.; Restrepo-Ruiz, M. Classifying Pattern and Feature Properties to Get a Θ(n) Checker and Reformulation for Sliding Time-Series Constraints. CoRR. 2019. abs/1912.01532. Available online: https://arxiv.org/abs/1912.01532 (accessed on 5 July 2023).
- Arafailova, E. Functional Description of Sequence Constraints and Synthesis of Combinatorial Objects. Ph.D. Thesis, IMT Atlantique, Nantes, France, 2018. [Google Scholar]
- Hien, A.; Beldiceanu, N.; Quimper, C.; Restrepo-Ruiz, M. Code and Supplementary Material. 2023. Available online: https://gitlab.com/postdochien/atisad (accessed on 5 July 2023).
- Stafford, G. Environmental Sensor Telemetry Data. 2020. Available online: https://www.kaggle.com/datasets/garystafford/environmental-sensor-data-132k (accessed on 5 July 2023).
- Morrill, J.; Fermanian, A.; Kidger, P.; Lyons, T.J. A Generalised Signature Method for Time Series. CoRR. 2020. abs/2006.00873. Available online: https://arxiv.org/abs/2006.00873 (accessed on 5 July 2023).
- Keogh, E.; Chu, S.; Hart, D.; Pazzani, M. Segmenting Time Series: A Survey and Novel Approach. In Data Mining in Time Series Databases; World Scientific: Singapore, 2004; Volume 57, pp. 1–21. [Google Scholar] [CrossRef]
- Veanes, M.; Hooimeijer, P.; Livshits, B.; Molnar, D.; Bjørner, N.S. Symbolic finite state transducers: Algorithms and applications. In Proceedings of the 39th ACM SIGPLAN-SIGACT, Philadelphia, PA, USA, 25–27 January 2012; pp. 137–150. [Google Scholar] [CrossRef]
- Crochemore, M.; Hancart, C.; Lecroq, T. Algorithms on Strings; Cambridge University Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Arafailova, E.; Beldiceanu, N.; Douence, R.; Carlsson, M.; Flener, P.; Rodríguez, M.A.F.; Pearson, J.; Simonis, H. Global Constraint Catalog, Volume II, Time-Series Constraints. CoRR. 2016. abs/1609.08925. Available online: https://arxiv.org/abs/1609.08925 (accessed on 5 July 2023).
- Sakarovitch, J. Elements of Automata Theory; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Hopcroft, J.E.; Motwani, R.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation, 3rd ed.; Pearson International Edition: London, UK, 2006. [Google Scholar]
- Kolev, B.; Akbarinia, R.; Jiménez-Peris, R.; Levchenko, O.; Masseglia, F.; Patiño, M.; Valduriez, P. Parallel Streaming Implementation of Online Time Series Correlation Discovery on Sliding Windows with Regression Capabilities. In Proceedings of the 9th International Conference on Cloud Computing and Services Science, Heraklion, Crete, Greece, 2–4 May 2019; SciTePress: Setúbal, Portugal, 2019; Volume 1, pp. 681–687. [Google Scholar]
- Kontaki, M.; Papadopoulos, A.N.; Manolopoulos, Y. Adaptive similarity search in streaming time series with sliding windows. Data Knowl. Eng. 2007, 63, 478–502. [Google Scholar] [CrossRef]
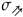 in a multivariate time series, (B) Transducer of pattern
in a multivariate time series, (B) Transducer of pattern 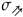 , (C) Accumulators updates.
, (C) Accumulators updates.
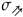 in a multivariate time series, (B) Transducer of pattern
in a multivariate time series, (B) Transducer of pattern 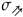 , (C) Accumulators updates.
, (C) Accumulators updates.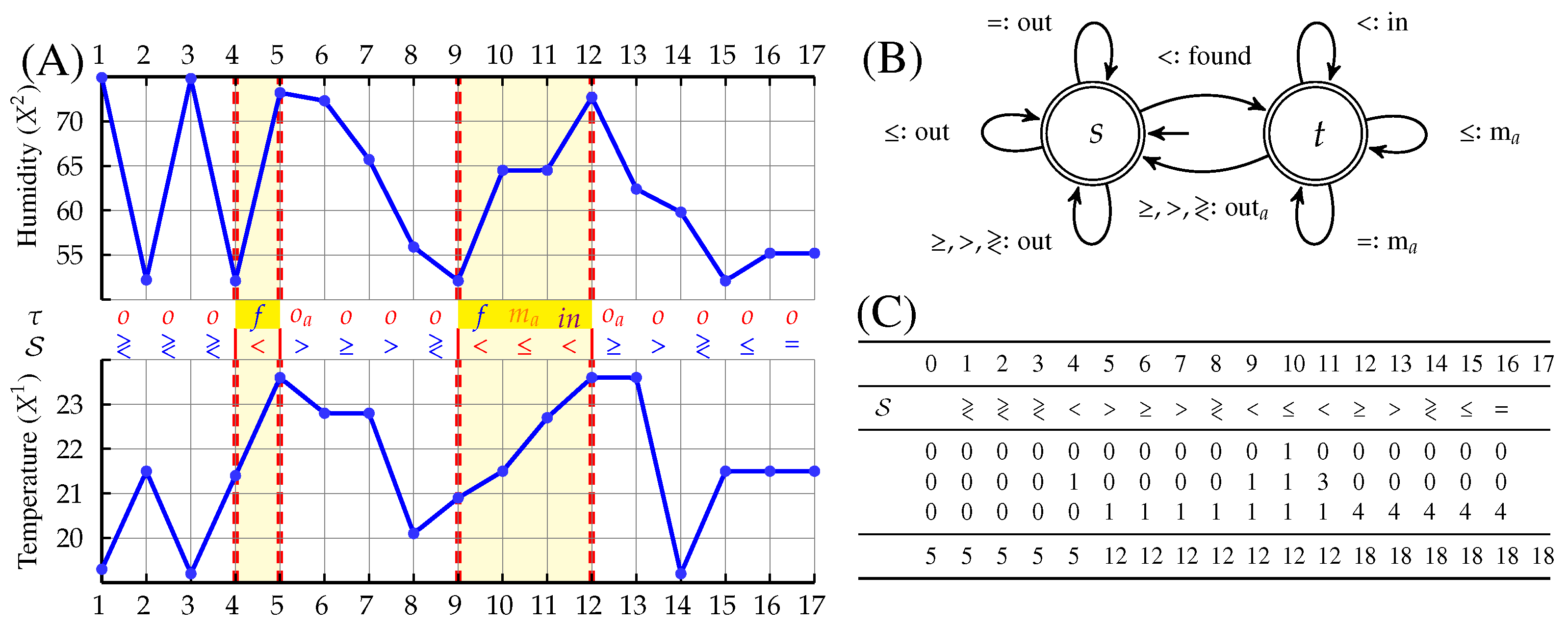
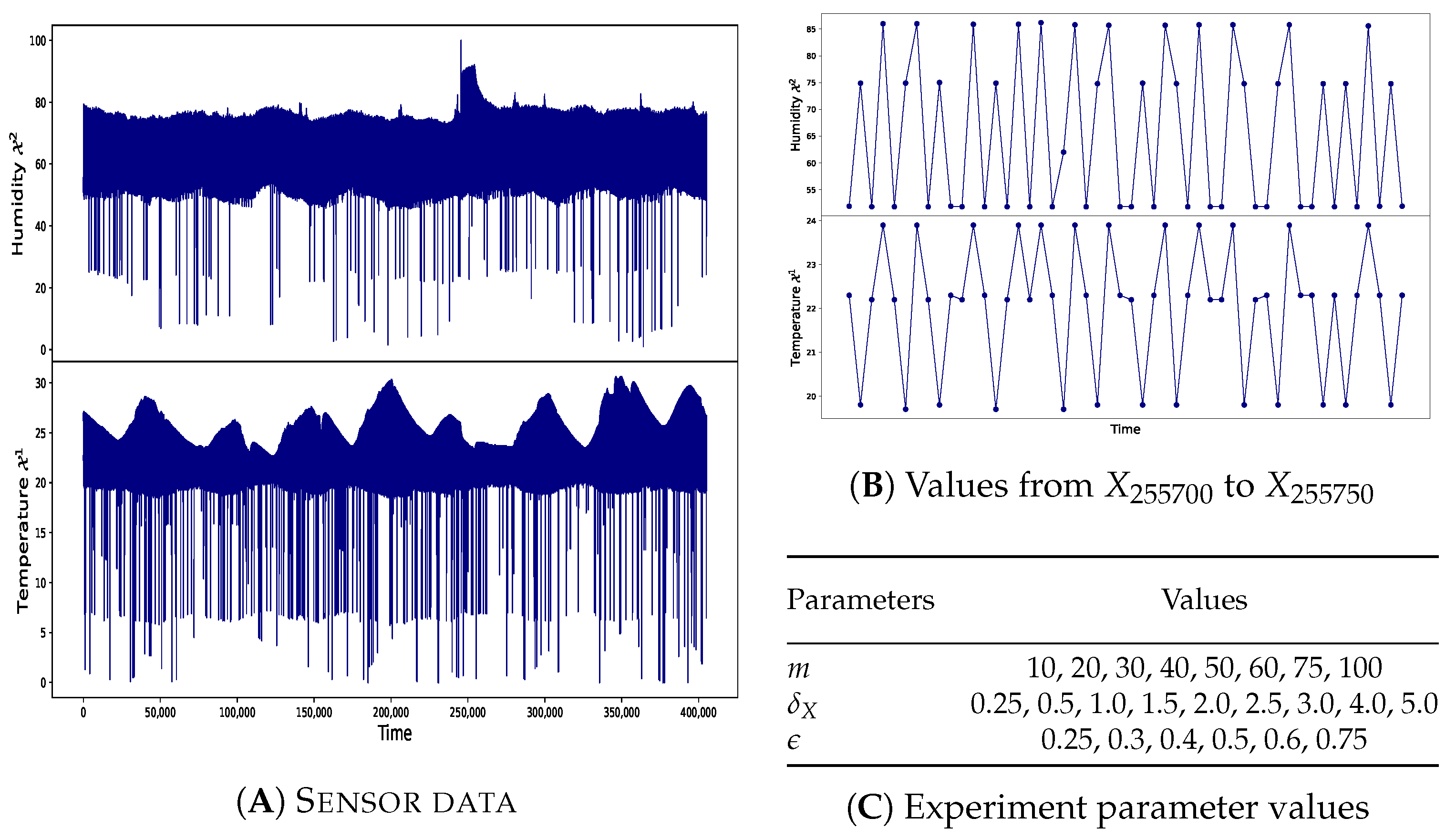
 and
and  , and varying the values of and . These problematic windows are plotted in red, the non-problematic windows remain in blue.
, and varying the values of and . These problematic windows are plotted in red, the non-problematic windows remain in blue.
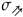 and
and  , and varying the values of and . These problematic windows are plotted in red, the non-problematic windows remain in blue.
, and varying the values of and . These problematic windows are plotted in red, the non-problematic windows remain in blue.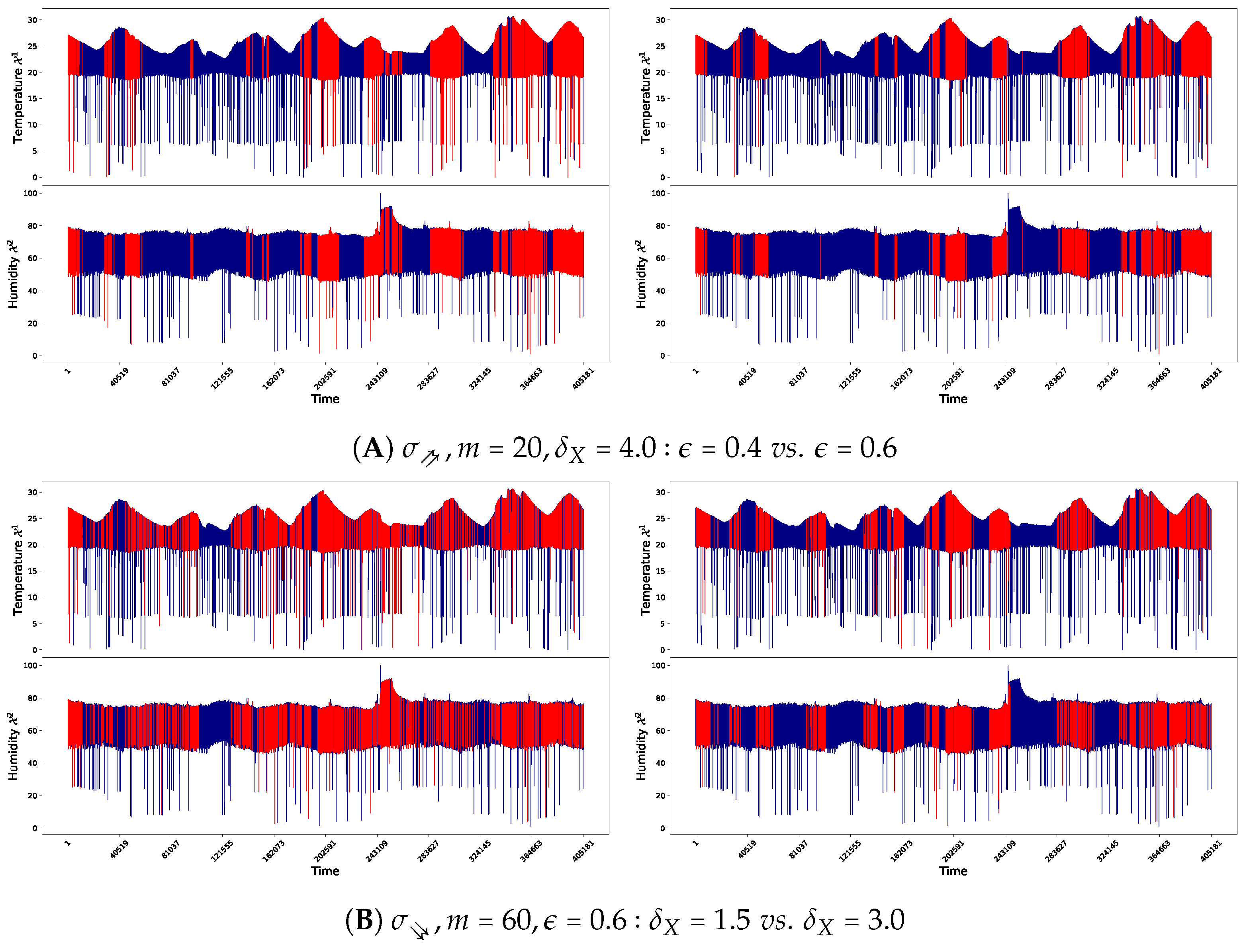
| Time | 1 am | 2 am | 3 am | 4 am | 5 am | 6 am | 7 am | 8 am | 9 am | 10 am | 11 am | 12 pm | 1 pm | 2 pm | 3 pm | 4 pm | 5 pm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp. (C) | 19.3 | 21.5 | 19.2 | 21.4 | 23.6 | 22.8 | 22.8 | 20.1 | 20.9 | 21.5 | 22.7 | 23.6 | 23.6 | 19.2 | 21.5 | 21.5 | 21.5 |
| Hum. (%) | 74.9 | 52.2 | 74.8 | 52.1 | 73.2 | 72.3 | 65.7 | 55.9 | 52.1 | 64.5 | 64.5 | 72.7 | 62.4 | 59.8 | 52.1 | 55.2 | 55.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hien, A.; Beldiceanu, N.; Quimper, C.-G.; Restrepo, M.-I. Automata Based Multivariate Time Series Analysis for Anomaly Detection over Sliding Time Windows. Eng. Proc. 2023, 39, 65. https://doi.org/10.3390/engproc2023039065
Hien A, Beldiceanu N, Quimper C-G, Restrepo M-I. Automata Based Multivariate Time Series Analysis for Anomaly Detection over Sliding Time Windows. Engineering Proceedings. 2023; 39(1):65. https://doi.org/10.3390/engproc2023039065
Chicago/Turabian StyleHien, Arnold, Nicolas Beldiceanu, Claude-Guy Quimper, and María-I. Restrepo. 2023. "Automata Based Multivariate Time Series Analysis for Anomaly Detection over Sliding Time Windows" Engineering Proceedings 39, no. 1: 65. https://doi.org/10.3390/engproc2023039065
APA StyleHien, A., Beldiceanu, N., Quimper, C.-G., & Restrepo, M.-I. (2023). Automata Based Multivariate Time Series Analysis for Anomaly Detection over Sliding Time Windows. Engineering Proceedings, 39(1), 65. https://doi.org/10.3390/engproc2023039065







