Applying Data Mining and Machine Learning Techniques to Predict Powerlifting Results †
Abstract
1. Introduction
2. Related Work
- Analysis of USA Powerlifting Federation data (2012–2016) [1]: This work highlights the importance of considering equipped and raw powerlifting as different sports, and the substantial differences in performance between the two disciplines. Squats and bench presses are much more affected by equipment than deadlifts due to their eccentric and concentric phases. Lifters do not benefit as much from equipment when performing deadlifts, since there is no eccentric phase. Given this, in our study, we analysed raw and equipped lifting separately, and also considered gender differences. Women tend to reach their plateau sooner than men, but their performance declines earlier. Males reach their peak performance later, but tend to hold it for a much longer time period. The ideal age for performance ranges from 24 to 39 years, with the mean age established at 30 years. This work [1] has some limitations, such as the limited amount of data and the tedious process of manually searching through the International Powerlifting Federation (IPF) website. In our study, we processed an already well-developed database from OpenPowerlifting. Published statistics in [1] regarding ages, weights, genders, raw vs. equipped, and exercises were used as a reference for further analysis. We complement this information with additional graphic resources and analyses, in order to gain further insights.
- Influence of Compressive Gear on Powerlifting Performance: Role of Blood Flow Restriction Training [2]: In this paper, the blood occlusion induced by compressive gear is described. The summary proposes that the occlusion can be maximum while performing squats. That is, the gear used in non-raw competitions can totally occlude the blood flow in the legs, which resulted in an increase in performance. What is more, this increase is not as significant either in bench presses or deadlifts. This may be due to the nature of the movement itself (deadlift) and the fact that it lacks an eccentric phase, or that it is impossible to totally occlude the muscles involved in the exercise (pectoral muscles in bench press) to such an extent as is possible with squats. The fact of the matter is, wearing such gear will still increase the performance in both movements, especially when compared to raw users, but not to the extent as in squats. However, the deadlift is the least affected out of the three. For these reasons, the idea of splitting the dataset into two different disciplines (raw vs. equipped) was reinforced.
- The Role of FFM Accumulation and Skeletal Muscle Architecture in Powerlifting Performance [3]: The importance of distinguishing between muscle mass and fat mass was explained in this study. Basically, it shows that more fat-free mass (FFM), i.e., muscle, is related to performance in powerlifting: the more the better. However, it is still limited by the muscle structure itself, as well as the muscle longitude and the degree in which those muscle fibres are distributed. All these variables are involved in determining how much strength each muscle section can produce. All in all, the more fat-free mass the lifter has, the stronger they will be, and stronger athletes tend to lift heavier weights, making them better-performing powerlifters.
- The Effect of Experimental Alterations in Excess Mass on Pull-Up Performance in Fit Young Men [4]: In this work, the authors explain how the differences in body fat percentage of a lean athlete (low body fat) and a heavier one (high body fat) can affect their pull-up and their bench press performance. To begin with, they show that there is a strong relationship between how heavy the lifter is (tall and/or muscular individual), or how high their body fat percentage is, and performance, since increasing body fat percentage by 10% will result in a significant reduction in performance (fewer repetitions). It is said that this could apply to other forms of exercise, such as the bench press. So, if an individual lifts 100 kg for eight repetitions, and this same individual adds 10 kg to the bar, they will then only be able to perform four repetitions, that is, half of what they achieved previously (assuming eight repetitions is close to the athlete’s maximum performance). It is shown that pull-ups are not as good at measuring an athlete’s performance as they are at measuring their bodyweight, either as body fat percentage or muscle mass. Essentially, this work showed us how important it is to take the athlete’s weight into consideration when analysing our own dataset, since variations in weight do make a difference.
- Adjusting Powerlifting Performances for Differences in Body Mass [5]: In this work, there is a comparison between the formulas of Stiff and Sinclair as well as other aspects that must be taken into consideration when working with a dataset similar to the one we used. It is said that the Stiff formula is better, since it works regardless of weight, and this makes it more accurate than the Sinclair formula. Additionally, it is advised that one separates the data for males and females, as well as raw and non-raw, and thus avoids mixing everything together. It also mentions that the larger the number of instances the better. The key lesson we learned from this study is that it is very important to split the database into different groups, even though, supposedly, the fact that one group is raw and the other is non-raw does not influence the results of the Stiff formula as much as it does the Sinclair formula, since the former does not use the weight variable in its calculations, whereas the latter does.
3. Dataset Description
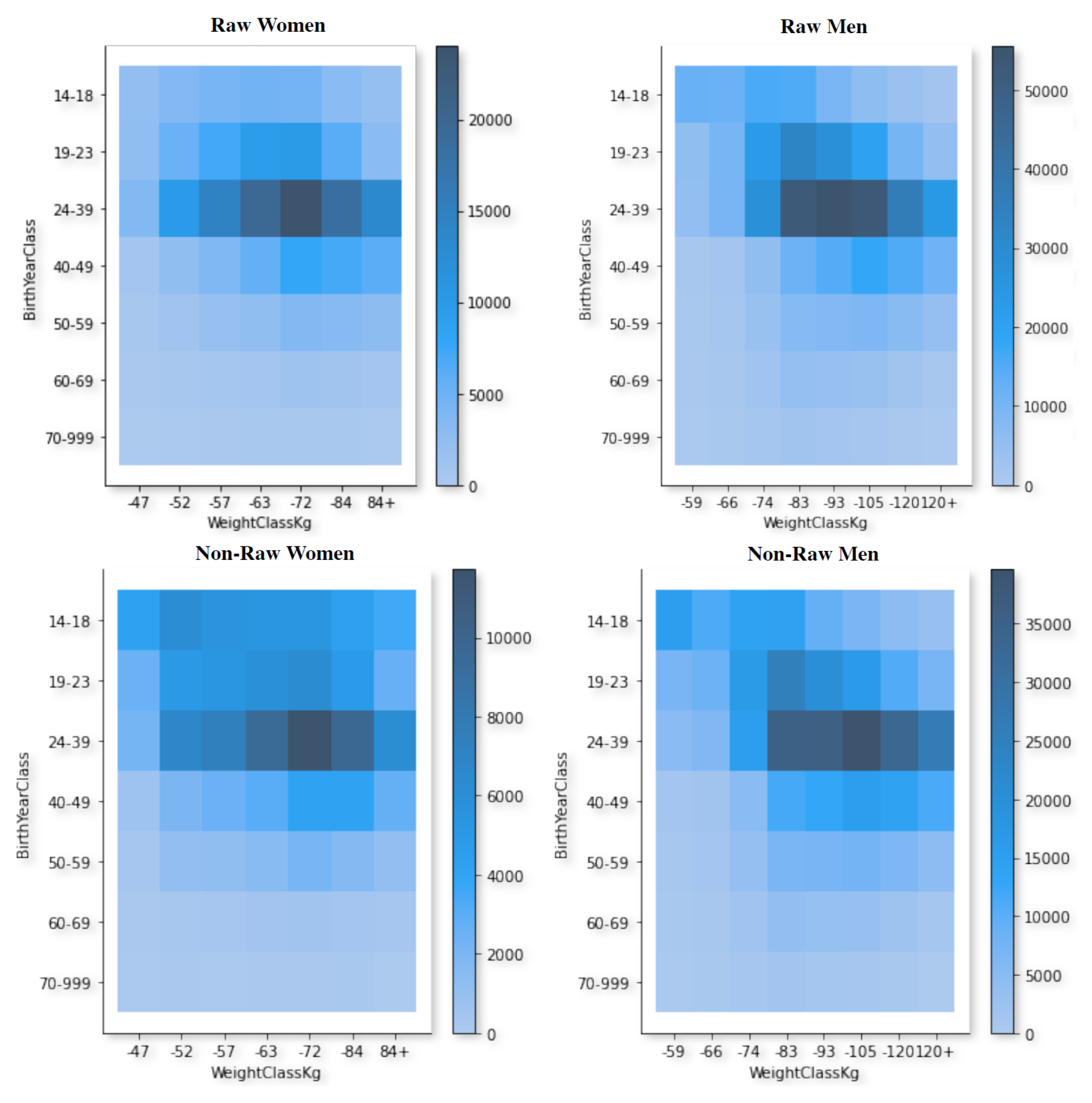
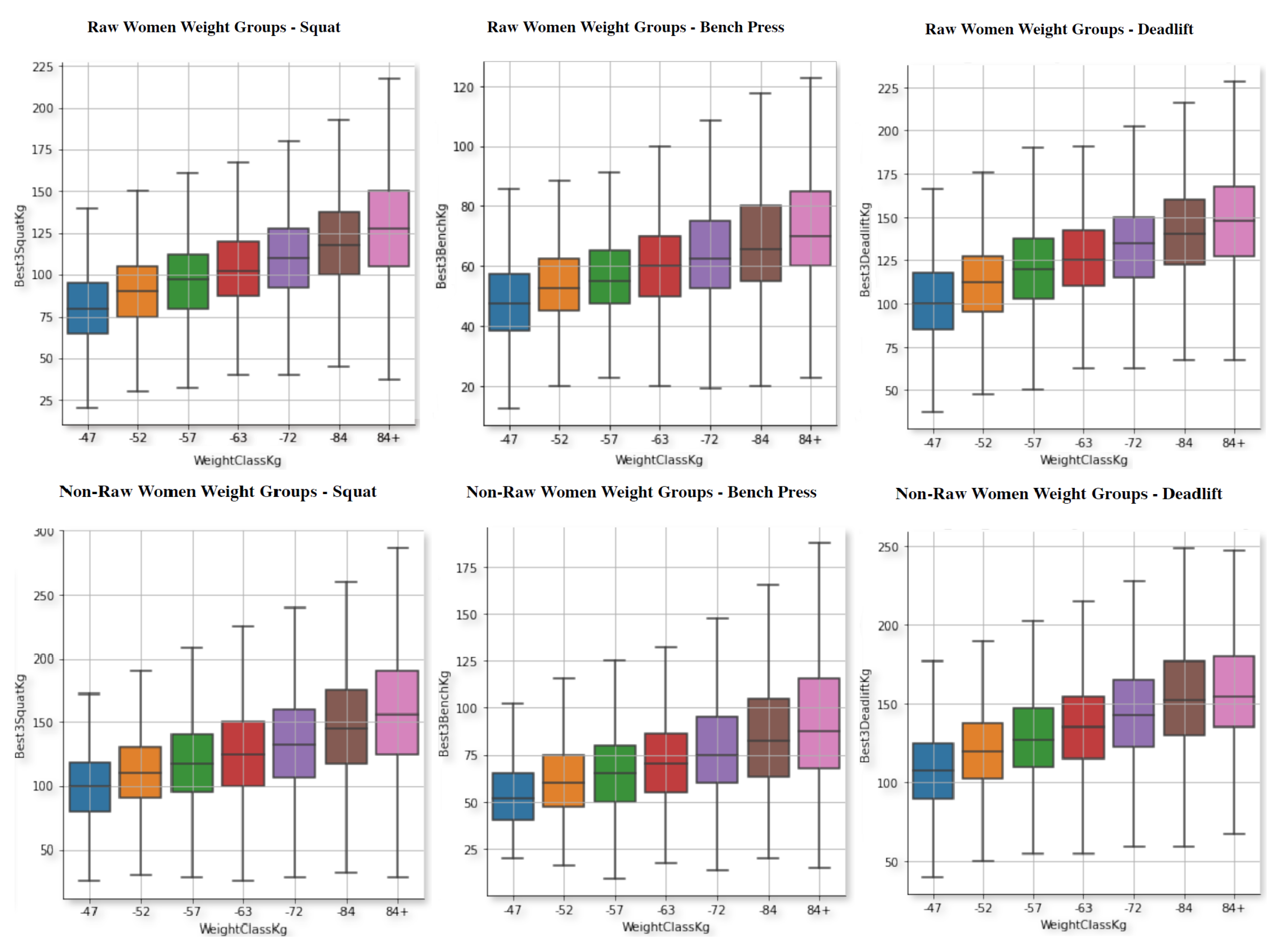
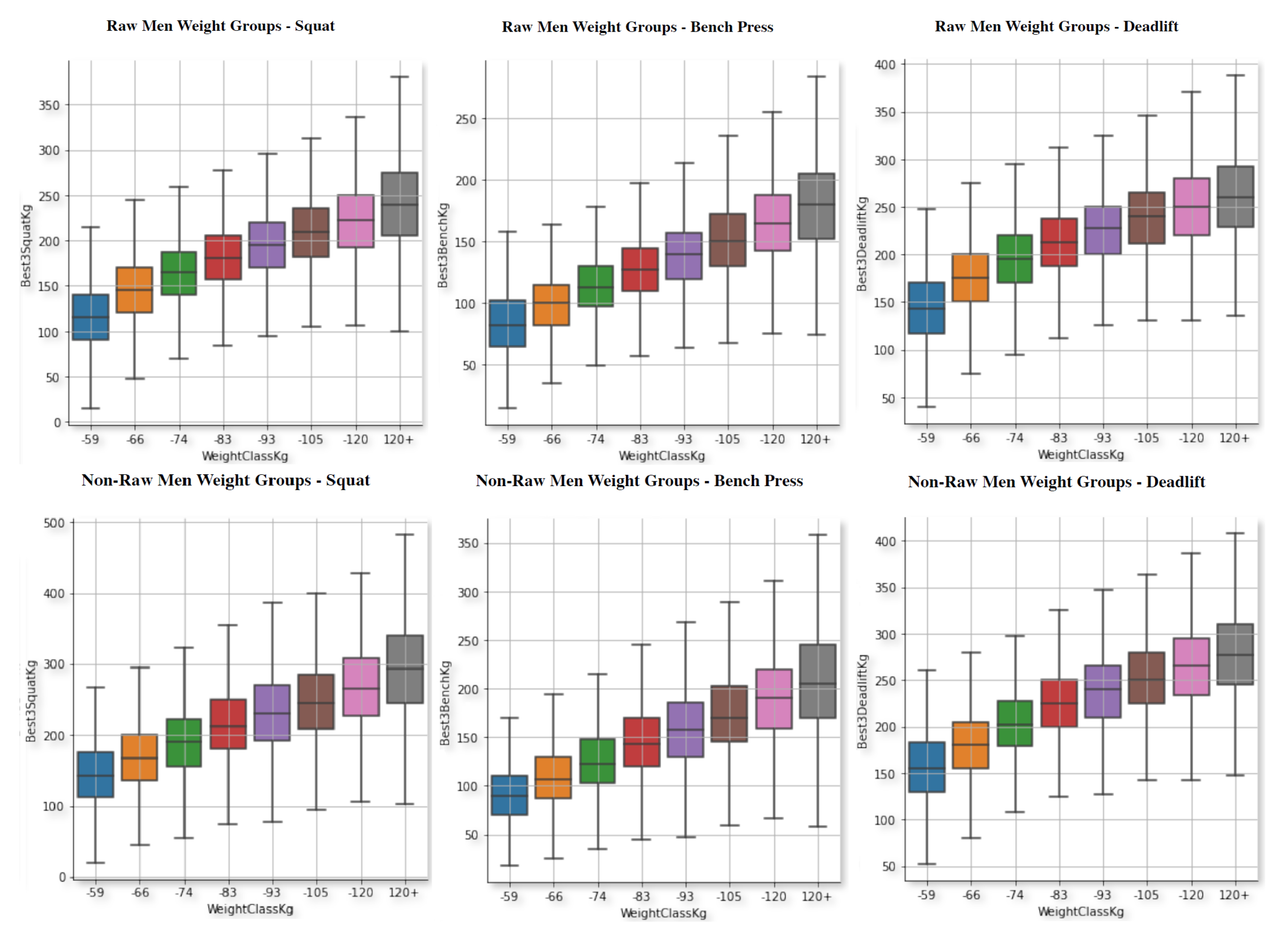
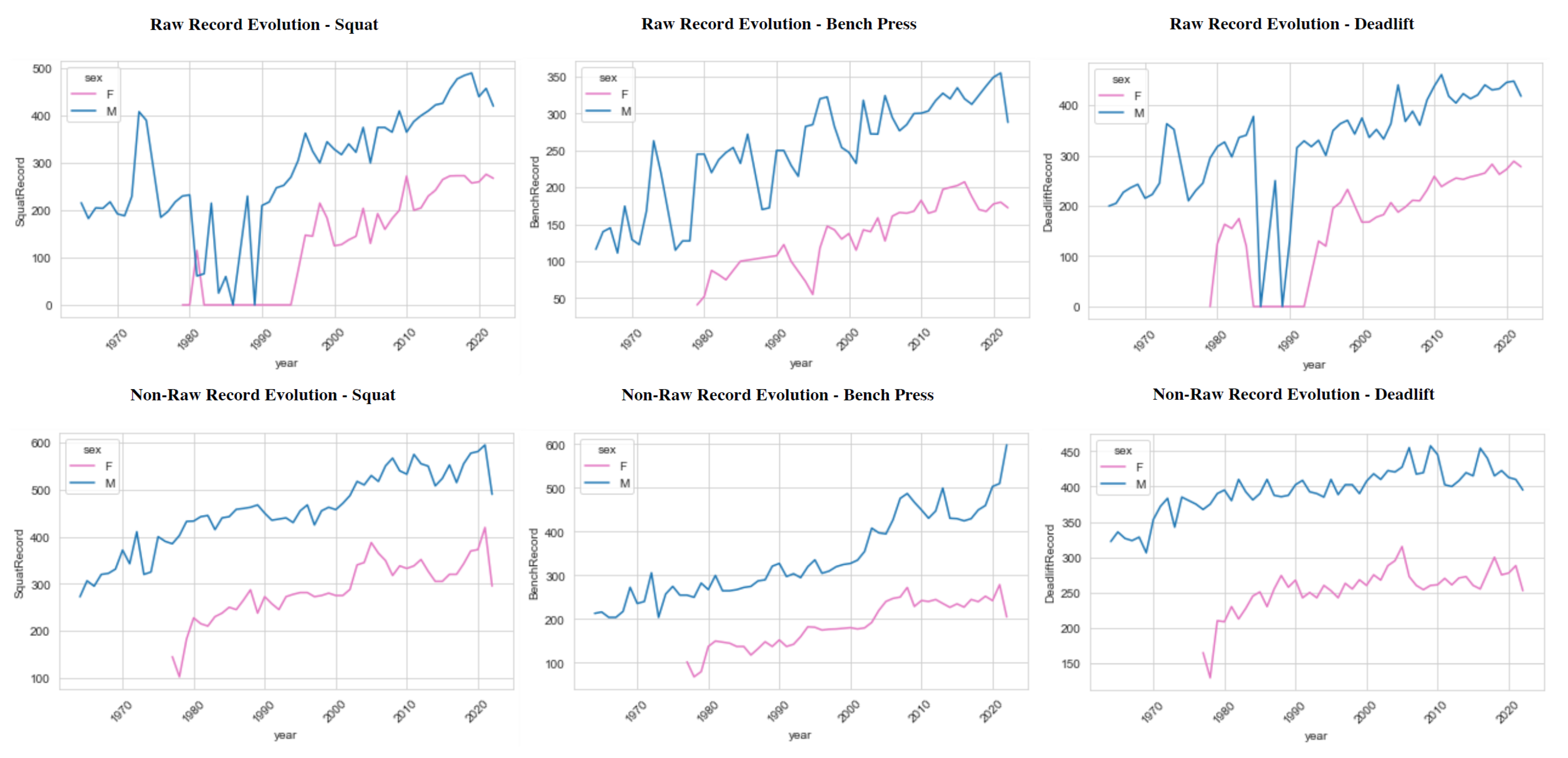
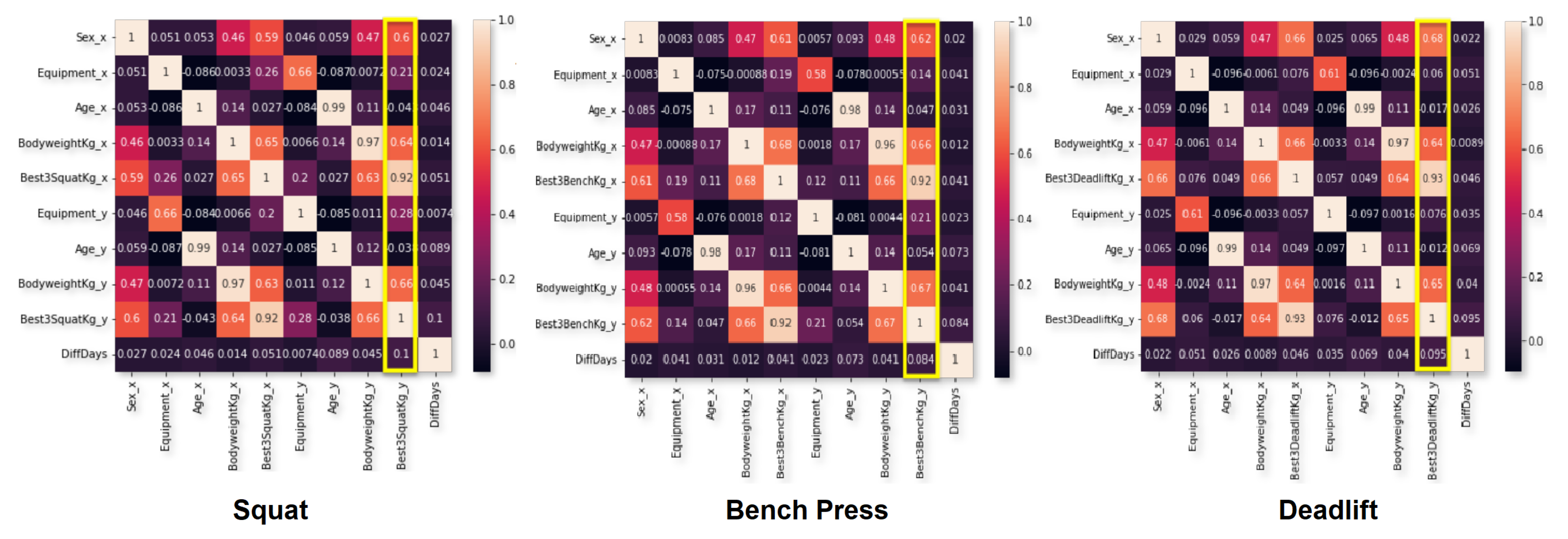
4. Exploratory Data Analysis
5. Regression Models
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ball, R.; Weidman, D. Analysis of USA powerlifting federation data from January 1, 2012–June 11, 2016. J. Strength Cond. Res. 2018, 32, 1843–1851. [Google Scholar] [CrossRef] [PubMed]
- Godawa, T.M.; Credeur, D.P.; Welsch, M.A. Influence of compressive gear on powerlifting performance: Role of blood flow restriction training. J. Strength Cond. Res. 2012, 26, 1274–1280. [Google Scholar] [CrossRef] [PubMed]
- Brechue, W.F.; Abe, T. The role of FFM accumulation and skeletal muscle architecture in powerlifting performance. Eur. J. Appl. Physiol. 2002, 86, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Vanderburgh, P.M.; Edmonds, T. The effect of experimental alterations in excess mass on pull-up performance in fit young men. J. Strength Cond. Res. 1997, 11, 230–233. [Google Scholar]
- Cleather, D.J. Adjusting powerlifting performances for differences in body mass. J. Strength Cond. Res. 2006, 20, 412–421. [Google Scholar] [PubMed]
- OpenPowerlifting. Available online: https://www.openpowerlifting.org (accessed on 25 May 2023).
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kramer, O.; Kramer, O. K-nearest neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–23. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the IEEE 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Edwards, W.; Von Winterfeldt, D.; Moody, D.L. Simplicity in decision analysis: An example and a discussion. In Decision Making: Descriptive, Normative, and Prescriptive Interactions; Cambridge University Press: Cambridge, UK, 1988; pp. 443–464. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3/E; Pearson Education India: Uttar Pradesh, India, 2009. [Google Scholar]
- Bickel, P.J.; Doksum, K.A. Mathematical Statistics: Basic Ideas and Selected Topics, Volumes I-II Package; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]



| # | VARIABLE | TYPE | DESCRIPTION |
|---|---|---|---|
| 1 | Name | string | Full name of each athlete |
| 2 | Sex | string | Gender of the athlete (‘F’ for females or ‘M’ for males) |
| 3 | Event | string | Whether it was a SBD competition with the three movements or just one or a combination of them |
| 4 | Age | float | The athlete’s age |
| 5 | AgeClass | string | The athlete’s age class |
| 6 | BodyweightKg | float | The athlete’s bodyweight |
| 7 | WeightClassKg | float | The athlete’s weight class |
| 8 | Best3SquatKg | float | The heaviest and correct lift in kg for squats recorded in the previous attempts |
| 9 | Best3BenchKg | float | The heaviest and correct lift in kg for bench presses recorded in the previous attempts |
| 10 | Best3DeadliftKg | float | The heaviest and correct lift in kg for deadlifts recorded in the previous attempts |
| 11 | TotalKg | float | The sum of the three best marks (in the three previous variables) |
| 12 | Place | float | The final position of that athlete in the competition |
| 13 | Dots | float | The result of applying the Dots formula to these values in order to rate the performance |
| 14 | Wilks | float | The result of applying the Wilks formula to these values in order to rate the performance |
| 15 | Glossbrenner | float | The result of applying the Glossbrenner formula to these values in order to rate the performance |
| 16 | Goodlift | float | The result of applying the Goodlift formula to these values in order to rate the performance |
| 17 | Tested | boolean | Records whether the athlete was drug tested or not |
| 18 | Parent Federation | string | The parent federation where the competition took place |
| 19 | Date | date | The date of the competition. Format: yy-mm-dd |
| RAW | NON-RAW | |
|---|---|---|
| Women | 227,700 | 151,500 |
| Men | 631,000 | 521,200 |
| TOTAL | 858,700 | 672,700 |
| Model | MSE | MAE | Score |
|---|---|---|---|
| Linear Regression | 580.22 | 15.95 | 0.88 |
| Lasso Regression | 583.09 | 16.00 | 0.88 |
| Ridge Regression | 580.22 | 15.95 | 0.88 |
| Random Forest | 433.59 | 13.56 | 0.91 |
| KNN | 504.64 | 14.93 | 0.90 |
| MARS | 580.22 | 15.95 | 0.88 |
| Decision Tree | 849.55 | 18.47 | 0.84 |
| ANN | 489.37 | 14.75 | 0.90 |
| Model | MSE | MAE | Score |
|---|---|---|---|
| Linear Regression | 358.92 | 12.10 | 0.88 |
| Lasso Regression | 362.29 | 12.14 | 0.88 |
| Ridge Regression | 358.92 | 12.10 | 0.88 |
| Random Forest | 193.86 | 8.53 | 0.94 |
| KNN | 260.39 | 10.34 | 0.92 |
| MARS | 358.89 | 12.10 | 0.88 |
| Decision Tree | 407.55 | 11.86 | 0.88 |
| ANN | 243.12 | 9.88 | 0.92 |
| Model | MSE | MAE | Score |
|---|---|---|---|
| Linear Regression | 413.61 | 13.10 | 0.88 |
| Lasso Regression | 416.12 | 13.13 | 0.88 |
| Ridge Regression | 412.27 | 13.07 | 0.88 |
| Random Forest | 280.51 | 10.57 | 0.92 |
| KNN | 351.06 | 12.38 | 0.90 |
| MARS | 418.07 | 13.21 | 0.88 |
| Decision Tree | 602.92 | 15.15 | 0.85 |
| ANN | 334.58 | 11.44 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Romero, J.; Mora, A.M.; Valenzuela-Valdés, J.F.; Castillo, P.Á. Applying Data Mining and Machine Learning Techniques to Predict Powerlifting Results. Eng. Proc. 2023, 39, 20. https://doi.org/10.3390/engproc2023039020
Medina-Romero J, Mora AM, Valenzuela-Valdés JF, Castillo PÁ. Applying Data Mining and Machine Learning Techniques to Predict Powerlifting Results. Engineering Proceedings. 2023; 39(1):20. https://doi.org/10.3390/engproc2023039020
Chicago/Turabian StyleMedina-Romero, Jorge, Antonio Miguel Mora, Juan Francisco Valenzuela-Valdés, and Pedro Ángel Castillo. 2023. "Applying Data Mining and Machine Learning Techniques to Predict Powerlifting Results" Engineering Proceedings 39, no. 1: 20. https://doi.org/10.3390/engproc2023039020
APA StyleMedina-Romero, J., Mora, A. M., Valenzuela-Valdés, J. F., & Castillo, P. Á. (2023). Applying Data Mining and Machine Learning Techniques to Predict Powerlifting Results. Engineering Proceedings, 39(1), 20. https://doi.org/10.3390/engproc2023039020








