Analysis and Research on Activity-Based Bottleneck Model ^†

Abstract

Based on Vickrey’s bottleneck model, we propose an activity-based bottleneck model to study traffic congestion on freeways during holidays. Based on the activity-based bottleneck model, we study the bottleneck ladder charging problem under the linear marginal activity utility and compare it with the traditional bottleneck model. Compared with the activity-based bottleneck model, the traditional bottleneck model overestimates the queue delay at the bottleneck, the level of step charging, and the start and end time of peak hours. Therefore, the activity-based step charging method disperses the traffic pressure on peak sections to a certain extent, avoiding traffic accidents caused by the transition period between charging and free.

1. Introduction

According to the notice of the State Council on Approving and transmitting the implementation plan of the Ministry of Transport and other departments on Exempting small bus tolls on major holidays, Guangxi Zhuang Autonomous Region has implemented the policy of exempting high-speed tolls for small buses with seven seats or less during major holidays since 2012. In recent years, with the continuous increase in vehicle ownership, short-distance and self-driving travel on holidays has increased, and the free traffic congestion and traffic accidents during holidays have also attracted much attention. According to the statistics released by Guangxi Expressway, during May Day this year, the traffic flow of the Expressway in the region is expected to be 3,784,600 vehicles (756,900 vehicles per day), a decrease of 51.2% over the same period in 2021 and an increase of 54.79% over the previous holiday. Among them, the traffic volume of small passenger cars with less than seven seats is 3,338,500 vehicles (667,700 vehicles per day).

From the perspective of expressway operation in the whole region, the traffic congestion sections are mainly concentrated in 29 Expressway sections, including Fujian Quanzhou to Guangxi Nanning Expressway (G72) of Guilin North Sujia interchange to Inner Mongolia Baotou to Guangdong Maoming Expressway (G65) of the bureaucratic Tian interchange section, the Bozhai to Luzhai section of G72, Lowe bridge section of G72, Nanning East toll station of G72, and Liujing toll station of G72. According to the analysis, the causes of congestion are large traffic flow, rear-end collisions, or scraping accidents. There are human behaviors in the transition stage between stopping and going, too. Drivers do not understand the detailed rules of exemption, so they slow down or stay at the entrance of the toll station until 0 o’clock to pass for free, resulting in a large number of queues at the entrance of the highway toll station, causing congestion. In addition, to leave the expressway before the start of charging, drivers are speeding or frequently changing lanes and overtaking, resulting in traffic accidents, which also causes Expressway congestion.

The policy of free highway access on holidays has caused many traffic problems, and there needs to be a perfect system to control congestion and ensure the normal service level of roads. There is considerable research and application on congestion pricing. In terms of theoretical research, in the 1980s, von Platen et al. [1] proposed a static congestion pricing model based on the marginal cost principle, which is also known as the marginal cost pricing model. On the basis of marginal cost pricing theory, Defermos et al. [2] studied the optimal congestion pricing model for general road networks and identified two types of congestion charging: path charging and road section charging, both of which can optimize the system. Yang et al. [3] extended the marginal charging pricing principle to general road networks and established an elastic congestion pricing model under the constraint that the capacity of road sections is limited. In 1993, Smith [4] presented a new dynamic model of peak period traffic flows on congested capacity-constrained urban road networks. While respecting the first in, first out (FIFO) discipline of road traffic queues and the exit capacities of road links, the model determines the (time-varying) costs incurred in traversing the various routes when (time-varying) route inflows are specified. It is proved that if this model is used to find route costs then a dynamic user equilibrium exists.

2. Related Work

2.1. Theoretical Research on Traditional Bottleneck Model

Vickrey [5] first proposed the classical bottleneck model in 1969. He assumed that there is a bottleneck road with limited traffic capacity connecting the residential and working places of residents, and the traffic capacity of other places except the bottleneck road is large enough. That is, only the bottleneck has crowded queues. Assuming that the traffic capacity of the bottleneck road is S vehicles/unit time, queuing occurs when the arrival rate of the bottleneck road exceeds S. Therefore; every traveler faces a trade-off between the cost of congestion time and the cost of planned delay. The basis of travelers’ decisions is to choose a departure time to minimize their travel costs. Under the equilibrium state of the bottleneck model, the total travel cost of all travelers is equal.

2.2. No Charge Cost

The travel cost of travelers is determined by the travel time ($\alpha$), early arrival time for work ($\beta$), and late time ($\gamma$) and is a linear function of

$$C\left(t\right)=\alpha +\beta +\gamma$$

(1)

If the travel cost ($C$) of all travelers is the same during the departure period, it reaches a balance. Assuming that the earliest person ($t_0$) and the latest person ($t_e$) do not encounter a queue, and $C\left(t_0\right)=C\left(t_e\right)=C$. Then, it is expressed as

$$\tau (t)\left\{\begin{array}{c}{t}_0=t^{\ast }-\frac{\gamma }{\beta +\gamma }\left[\frac{N}{S}\right]\\ t_e=t^{\ast }+\frac{\gamma }{\beta +\gamma }\left[\frac{N}{S}\right]\end{array}\right.$$

(2)

where $t^{\ast }$ is the ideal arrival time. The cost of travel for each person is

$$C=\frac{\beta \gamma }{\beta +\gamma }\left[\frac{N}{S}\right]=\delta \frac{N}{S}$$

(3)

where $\delta =\beta \gamma /(\beta +\gamma )$.

According to the research results of Arnott et al., the Total Travel Cost ($TTC$), Scheduled Delay Cost ($SDC$), and Trip Cost ($TC$) are defined as

$$TTC=SDC=\frac{\delta }{2}\left[\frac{N^2}{S}\right]$$

(4)

$$TC=TTC+SDC=\delta \left[\frac{N^2}{S}\right]$$

(5)

2.3. Social Optimum

The $TC$ of the system is minimized as the social optimum. Three conditions must be satisfied. (1) Bottleneck roads operate at full capacity during the peak period, (2) the departure rate must not be higher than the capacity, and (3) the earliest departure and the latest departure have the same planned delay cost. Then,

$$TTC=0,{TC}^0=TTC+SDC=\frac{\delta }{2}\left[\frac{N^2}{S}\right]$$

(6)

where ${TC}^0$ is the socially optimal $TC$. From the condition, the $TC$ of all travelers during the peak time is $\delta \frac{N}{S}$, and the departure and arrival rates are $s$. The dynamic charge can be obtained as

$$\tau (t)\left\{\begin{array}{c}\delta \left[\frac{N}{S}\right]-\beta \left(t^{\ast }-t\right),t\in [t_0,t^{\ast }]\\ \delta \left[\frac{N}{S}\right]-\gamma \left(t-t^{\ast }\right),t\in [t^{\ast },t_e]\end{array}\right.$$

(7)

The socially optimal dynamic toll is composed of two linear functions with different slopes, and $t^{\ast }$ attains its maximum value. Each traveler adjusts the departure time accordingly, thus eliminating queues and halving the $TC$.

3. Method

3.1. Tiered Charging Based on Activity-Based Bottleneck Model

Through the analysis of data over the years, we find that the peak period of the highway during holidays shows a regular distribution, mainly divided into three peak periods with the same pattern. We assume that the peak period of a peak section is from $t_p$ to $t_q$. According to the classical bottleneck model, Equation (7) shows that dynamic toll is a function of the time change, and it is difficult for travelers to accurately measure their toll amount and thus reasonably arrange their travel time. Therefore, in real life, ladder charging is often used to replace dynamic charging, which has high operability and strong applicability.

In this system, the first traveler and the last traveler do not need to queue, that is $T\left(t_p\right)=T\left(t_q\right)=0$. Thus, $\tau \left(t_p\right)=\tau \left(t_q\right)=0$. Under the equilibrium condition, the dynamic charge at the bottleneck can be obtained as

$$\tau (t)\left\{\begin{array}{c}{\int }_{t_p}^t{u}_l\left(t\right)dt+{\int }_t^{t_p}{u}_r\left(t\right)dt+\beta \left(t-t_p\right),t\in [t_p,t^{\ast }]\\ {\int }_{t_q}^t{u}_l\left(t\right)dt+{\int }_t^{t_q}{u}_r\left(t\right)dt+\gamma \left(t_q-t\right),t\in [t^{\ast },t_q]\end{array}\right.$$

(8)

where $u_l\left(t\right)$ and $u_r\left(t\right)$ are marginal functions.

3.2. Optimal Step Charge Model of Linear Function

According to the empirical research of Tseng et al., the marginal utility based on the activity method is a linear function that changes with time. The marginal utility of leaving home decreases with time, and the time utility of returning home increases with time [6,7]. Thus, the following equations are obtained.

$$\left\{\begin{array}{c}{u}_l\left(t\right)=g_0+g_{1}t, g_1<0\\ u_r\left(t\right)=h_0+h_{1}t, h_1>0\end{array}\right.$$

(9)

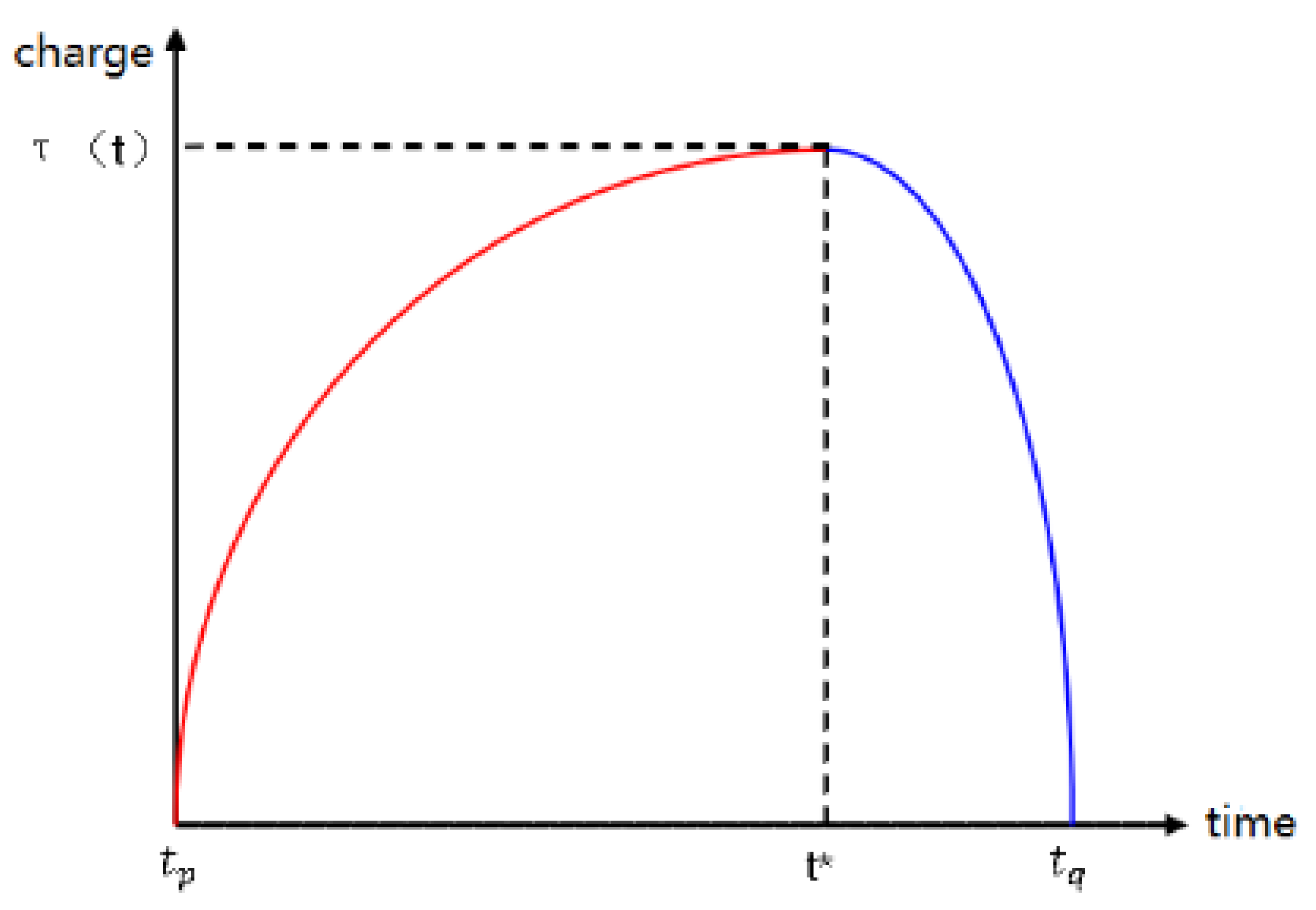
Bring the above equations into Equation (8), we obtain

$$\tau (t)\left\{\begin{array}{c}\frac{k_1}{2}{t}^2+\left(k_2+\beta \right)t-\left[\frac{k_1}{2}{\left(t_p\right)}^2+\left(k_2+\beta \right)t_p\right],t\in [t_p,t^{\ast }]\\ \frac{k_1}{2}{t}^2+\left(k_2-\gamma \right)t-\left[\frac{k_1}{2}{\left(t_q\right)}^2+\left(k_2-\gamma \right)t_q\right],t\in [t^{\ast },t_q]\end{array}\right.$$

(10)

where, $k_1=g_1-h_1, k_2=g_0-h_0$. The piecewise conic is obtained, as shown in Figure 1. At the same time, the peak start and end time can be calculated as follows.

$$\left\{\begin{array}{c}{t}_p=\frac{\left(\beta +\gamma \right)t^{\ast }+\frac{1}{2}{k}_1{\left(\frac{N}{S}\right)}^2+(k_2-\gamma )\left(\frac{N}{S}\right)}{\left(\beta +\gamma \right)-k_1\left(\frac{N}{S}\right)}\\ t_q=t_p+\frac{N}{S}\end{array}\right.$$

(11)

3.3. The Optimal Step Charge Based on Laih Model

The Laih model is used for step charging in the relevant bottleneck model, which is widely used in step charging due to its simplicity and real-time nature, such as in congestion charging in Singapore [8,9].

The optimal toll level $\rho$, toll start time $t^{+}$ and end time $t^{-}$ are determined first to satisfy $\rho =\tau \left(t^{+}\right)=\tau \left(t^{-}\right)$. The core idea of congestion charging is to replace queues at congestion with tolls, and the total revenue from maximizing step tolls must equal the maximum elimination of queues. Therefore, the charge level, the start time, and the end time of the charge should meet the following equations.

$$\left\{\begin{array}{c}\frac{k_1}{2}{{(t}^{+})}^2+\left(k_2+\beta \right)t^{+}-\left[\frac{k_1}{2}{\left(t_p\right)}^2+\left(k_2+\beta \right)t_p+\rho \right]=0\\ \frac{k_1}{2}{{(t}^{-})}^2+\left(k_2-\gamma \right)t^{-}-\left[\frac{k_1}{2}{\left(t_q\right)}^2+\left(k_2-\gamma \right)t_q+\rho \right]=0\end{array}\right.$$

(12)

The start time and the end time of the charge are as follows.

$$\left\{\begin{array}{c}{t}^{+}=\frac{-\left(k_2+\beta \right)+\sqrt{A}}{k_1}\\ t^{-}=\frac{-\left(k_2-\gamma \right)+\sqrt{B}}{k_1}\end{array}\right.$$

(13)

where $A={\left(k_2+\beta +k_1{t}_p\right)}^2+2k_{1}p, B={\left(k_2-\gamma +k_1{t}_q\right)}^2+2k_{1}p$, and according to the optimal conditions, the following equation can be obtained.

$$(\sqrt{A}+\sqrt{B})\left(1+\frac{\rho k_1}{\sqrt{AB}}\right)-\left(\beta +\gamma \right)=0$$

(14)

By solving the above equation, we can finally determine values of $\rho$, $t^{+}$ and $t^{-}$.

4. Experiments and Discussion

This section lists data for numerical analysis of the previous derivation results. The input parameters of the example are shown in

Table 1. Example input parameters.

N (Vehicle): 5000	S (vehicle/hour): 2000	${\mathit{t}}^{\mathbf{\ast }}$ (hour): 12:00
$\alpha$ (yuan/hour): 10.0	$\beta$ (yuan/hour): 6.0	$\gamma$ (yuan/hour): 19.0
$u_l$: 11.0	$u_r$: 8.0	$g_0$: −1/2
$g_1$: 10.0	$h_0$: 5/6	$h_1$: 2.0

[10]. The total number of commuters N is 5000 vehicles, and the traffic capacity S of the bottleneck is 2000 vehicles per hour. Therefore, the duration of the whole early peak period is 2.5 h.

The simulation experiment of step charging is carried out in two ways: Vickrey’s classic bottleneck model and the activity-based bottleneck model. The results are shown in

Table 2. Comparison results of step charges under different bottleneck models.

Model Solution	Travel-Based Bottleneck Model	Bottleneck Model Based on Activity Method
Maximum optimal dynamic charge $\tau \left(t^{\ast }\right)$ (yuan)	11.40	7.51
Optimal step charge $\rho$ (yuan)	5.70	4.17
Charge start time $t^{+}$	08:03	07:48
Charge end time $t^{-}$	09:18	09:09
Step charging time length $t^{+}-t^{-}$ (hours)	1.25	1.35

.

In real life, public travelers are rarely aware of the external diseconomy caused by their travel behavior. Although congestion charging can improve travel efficiency, most of the public is more or less opposed to this policy. In Table 2, the tiered charge based on the activity bottleneck model ρ is far lower than the traditional tiered charging level based on the travel bottleneck model and is easier to be accepted by the public.

Table 2 also shows the comparison of the tiered charging solutions under different bottleneck models. The step charging time length of the first model is 1.25 h, and the step charging time interval of the second model is 1.35 h. Moreover, the start time of the second model is the earliest, and the start time of the first model is the latest. Under the optimal step charge, the traditional trip-based bottleneck model has the highest charge level, indicating that the trip-based bottleneck model overestimates the congestion charge level. Therefore, compared with the traditional trip-based bottleneck model, the activity-based bottleneck model improves the charging efficiency, that is, eliminates the queuing phenomenon when the charge is lower.

5. Conclusions

According to the problems of traffic congestion and frequent accidents on freeways during holidays, we propose a bottleneck model based on the activity method, which charges congestion fees according to the density of road congestion to regulate the travel time, travel mode, and travel path and alleviate traffic congestion to a certain extent. Although tiered charging cannot eliminate congestion and queue, it can disperse road traffic pressure to the greatest extent. Highway operation managers can timely release information to inform travelers, provide travel advice, travel path planning, and other services for travelers and improve the service level of operation management.