Abstract
We established a group contribution (GC) parametrization for the heat of formation of organic molecules, but, and this is new, revealed chemical accuracy (1 kcal/mol). Compared to previous approaches which did not achieve this result, we succeeded by (i) taking reliable and consistent experimental data, (ii) not relying on computer-assisted automated parameter estimation, (iii) taking into account the physico-chemistry known for years, i.e., only introducing additional parameters when we understand the physico-chemistry, and finally, (iv) acknowledging that the linear additive GC method has its limits and cannot account properly for any molecule. Not only the averaged absolute deviations but also the individual results were almost without exception within chemical accuracy, except for some more heavily substituted molecules for which the group contribution approach breaks down.
1. Introduction
The group contribution (GC) approach is an old [1] approach and has been, over the course of time, developed for many molecular properties. The basic idea is illustrated in the scheme below Figure 1 where the molecule is broken into building blocks, the groups, and we also see the groups that constitute 2-methyl-1-propanol. The GC approach inherently assumes that the groups behave independently, and the value of a molecular property is calculated from the sum of the individual properties of the groups by:
ΔHf (molecule) = Σ Hf group contribution of constituting groups
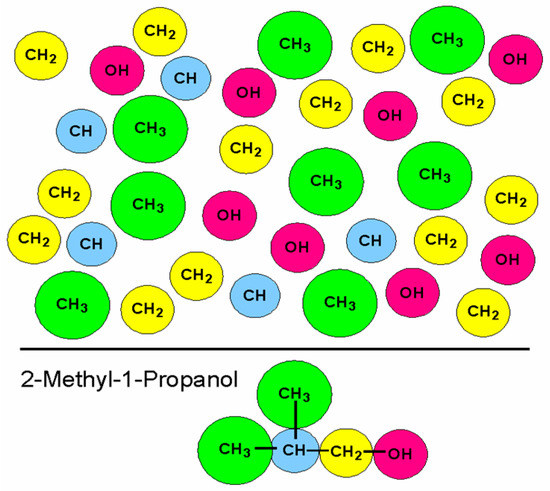
Figure 1.
Schematic representation of the Group Contribution (GC) concept where the molecule is broken into building blocks. On the top we have an assembly of chemical Groups which are the building blocks, in the context of the GC concept, defined to construct molecules such as 2-methyl-1-propanol shown. Different GC approaches might follow a different definition of the individual groups (see also text for further detail).
These quick and easy-to-use GC methods, in particular when a graphical interface is provided (e.g., the ICAS program suite [2]), are very beneficial for chemical process developers. One of these properties is the heat of formation ΔHf of organic molecules. To appropriately describe chemical transformations and equilibria, the heat of formation must have chemical accuracy, i.e., 1 kcal/mol or better. Moreover, the method must be reliable, which means there should be no or, really, very few outliers. So not only should the absolute average deviation of the model values be small but each individual value should be within chemical accuracy. Up until recently, GC methods for the heat of formation of organic molecules have not achieved chemical accuracy [3,4].
2. Results
We started an attempt to revise the GC approach for ΔHf and, in the meantime, we succeeded in achieving this goal [5,6,7,8]. Compared to previous approaches, this positive outcome was the result of a number of specific actions. First of all, in the procedure to determine the numerical values for the group contribution parameters, we almost exclusively used reliable and consistent experimental data selected after consulting with experts on experimental thermodynamics, which is crucial because of the 1 kcal/mol requirement. Previous attempts have often relied on the use of experimental heats of formation from databases, but these are generally collections of data from a large variety of literature sources without critical screening. Recently, Chan reported [9] that for the NIST database [10], the heat of formation of only less than 40% of all species included was found within chemical accuracy. Moreover, even pretty normal organic molecules such as 2-methyl-4-methylene-1,3-dioxolane and 2,4-dimethyl-1,3-dioxole were found to be off by more than 100 kJ/mol. When we use reliable data from proper sources, i.e., those from Rossini and co-workers on linear alkanes [11], we observe a very constant increment and a very small averaged absolute difference (AAD) between the experiment and GC model: 0.19 kJ/mol. It is interesting to note that when we take further experimental data from other sources for longer alkanes, i.e., heneicosane up until and including hexatriacontane, the AAD for these is only over 1 kJ/mol, which, although as such is still very good, is much larger than for the consistent Rossini data and that for simple compounds such as the linear alkanes. Next, for the GC parameter value for the CH2 group of −20.63 kJ/mol, at the same time, we obtained a unique GC parameter value for the CH3 group: −42.36 kJ/mol.
Secondly, in order to achieve chemical accuracy, we observed that we needed to determine the parameters step-by-step, by hand in fact, so that we could identify specific deviations. Most of the time, researchers use automated procedures in which larger amounts of data are optimized simultaneously, but this makes it virtually impossible to trace and understand specific deviations. One obtains a mathematical fit without the guarantee that the correct chemistry is represented. Rather than looking at individual data, more parameters are introduced to obtain better agreement with the experimental data, which easily leads to overfitting and incorrect predictions for molecules that were not involved in establishing the group contribution parameter values. Our procedure, as we learned through our recent investigations [5,6,7,8], resulted in an absolute minimum number of GC parameters, thereby avoiding overfitting, as additional parameters are only added based on concrete information on deviations between the model and experimental data and understood based on physico-chemical information. We have illustrated this with various examples [5,6,7,8].
Starting from the linear alkanes, the next step was the methyl-branched alkanes. Analysis of the experimental data in conjunction with the GC model revealed that we can achieve good model results when adding nearest-neighbor interactions. Using the concept of nearest- and next-nearest-neighbor interactions is quite common in physics and chemistry, and these can, if desired, also be confirmed by ab initio quantum calculations [8]. The latter provides us with a good physico-chemical justification for these additional parameters. The various neighbor interaction parameters we thus established are shown in Figure 2, where the one in yellow is the 1,5-Me-Me interaction.
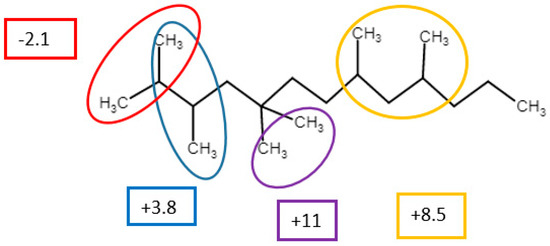
Figure 2.
Illustration of the corrections accounting for methyl-methyl interactions we have introduced. The numerical values indicated apply to the presence of the associated (same colour) methyl-methyl pairs [6].
An interesting example is formed by nitriles. Whereas for the mononitriles we see good agreement between the model and experiment, for the dinitriles this is not the case for the first two in the series, viz. Table 1. Various models describe these two well but require additional (not a priori justified) parameters to account for the higher dinitriles. In reality, one should look at it exactly the other way around: malono- and butanedinitrile are distinct cases because they are subject to so-called germinal effects. These were described in detail by Beckhaus et al. [12], who reported synergetic destabilization by two relatively close geminal cyano substituents of 48 kJ/mol, which is relatively close to the deviation of almost 55 kJ/mol presented in Table 1. So here as well, accounting for the correct physico-chemistry leads to a good and scientifically justified model.

Table 1.
Experimental [10] and model values for mono- and dinitriles. All values are in kJ/mol. The AAD for the dinitriles is based on the two last species only; for the discussion, see the text.
Another case in which it was not possible to obtain good agreement between the model and the experimental values, within chemical accuracy, was alkyl-ethers. However, when we calculated the geometries using quantum calculations (B3LYP), we could establish a relationship between the COC valence angle and the magnitude of the GC parameter value associated with the ether group. The relevant data have been collected together in Table 2, and we observed very good results within chemical accuracy.

Table 2.
Experimental and model values for various ethers. All values in kJ/mol.
A further crucial aspect is the relevant size of the chemical groups rather than using the smallest possible entities, which is often carried out, e.g., an aromatic carbon atom in a benzene ring rather than the benzene ring as the group. In various cases, the definition of groups that are not the smallest enabled very good results, i.e., chemical accuracy, which could not be obtained otherwise. It should not be surprising that we need to define larger entities as groups for, as a typical example, (heterogeneous) aromatic ring systems. The electronic interactions make the individual atoms (e.g., the CH entity cannot be regarded as an independent entity), and thus, the GC concept breaks down at least when we want to achieve good accuracy of prediction. Thus, in the case of pyridines and quinolones, we adopted these two molecules as groups themselves. When we combined this with our already established GC model (the parameters for the other groups), we obtained very good agreement between the model and the experiment, viz. Table 3.

Table 3.
Experimental [14] and GC model heats of formation for selected pyridines and quinolones. All values are in kJ/mol. Both pyridine and quinoline were adopted as a group themselves and are therefore indicated with an *.
Finally, it is important to realize and to make explicit that certain effects, i.e., certain molecules, cannot be treated by a simple linear additive method, which is what the GC method is. One example is the (substituted) cycloalkanes, where we have shown that by using quantum calculations of the G4 type [15], we can establish trends and we can extract additional parameters to be added to the GC model, leading to model values within chemical accuracy [8]. Another example is heavily substituted alkyl-substituted species. Whereas 3,5,5-trimethyl-1-hexanol and 2,2,4,4-tetramethyl-3-pentanol were well accounted for, this was not the case for 2,2,4,4-tetramethyl-3-iPr-3-pentanol (33 kJ/mol deviation). We could show that by using B3LYP quantum calculations, one can find out whether a case cannot be treated with the linear additive GC approach [8].
3. Conclusions
In summary, we established a new GC parametrization for the heat of formation of organic molecules for which not only averaged absolute deviations but also individual results were almost without exception within chemical accuracy, except for some more heavily alkyl-substituted molecules for which the group contribution approach breaks down.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors sincerely thank Sergey Verekvin (University of Rostock) and Jurgen Rarey for the discussion and advice on the quality of the experimental data, Paul Rablen (Swarthmore College, Swarthmore, PA, USA) for the joint work reported in Reference [8], and Georgios Kontogeorgis and Gürkan Sin (Danish Technical University, DTU) for allowing the use of the ICAS23 software suit.
Conflicts of Interest
The author declares no conflict of interest.
References
- Van Krevelen, D.W.; Chermin, H.A.G. Estimation of the free enthalpy (Gibbs free energy) of formation of organic compounds from group contributions. Chem. Eng. Sci. 1951, 1, 66–80, Erratum in Chem. Eng. Sci. 1952, 1, 238. [Google Scholar] [CrossRef]
- ICAS23 Software Package Which Includes the Marrero-Gani Method as Well as the Constantinou-Gani Approach and Also Provides Results Based on the Joback and Reid GC Method. Available online: https://www.kt.dtu.dk/english/research/kt-consortium/software (accessed on 21 February 2023).
- Hukkerikar, A.S.; Meier, R.J.; Sin, G.; Gani, R. A method to estimate the enthalpy of formation of organic compounds with chemical accuracy. Fluid Phase Equilibria 2013, 348, 23–32. [Google Scholar] [CrossRef]
- Kadda, A.; Mustapha, B.A.; Yahiaoui, A.; Khaled, T.; Hadji, D. Enthalpy of Formation Modeling Using Third Order Group Contribution Technics and Calculation by DFT Method. Int. J. Thermodyn. 2020, 23, 34–41. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy”. ChemEngineering 2021, 5, 24. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy” Part II. AppliedChem 2021, 1, 111–129. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy” Part III. AppliedChem 2022, 2, 213–228. [Google Scholar] [CrossRef]
- Meier, R.J.; Rablen, P.R. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy” Part IV. Thermo 2023, 3, 289–308. [Google Scholar] [CrossRef]
- Chan, B. High-Level Quantum Chemistry Reference Heats of Formation for a Large Set of C, H, N, and O Species in the NIST Chemistry Webbook and the Identification and Validation of Reliable Protocols for Their Rapid Computation. Phys. Chem. A 2022, 126, 4981–4990. [Google Scholar] [CrossRef] [PubMed]
- NIST Data Base. Available online: https://webbook.nist.gov/ (accessed on 16 March 2023).
- Prosen, E.J.; Rossini, F.D. Heats of combustion and formation of the paraffin hydrocarbons at 25 °C. J. Res. Natl. Bur. Stand. 1945, 34, 263–269. [Google Scholar] [CrossRef]
- Beckhaus, H.-D.; Dogan, B.; Pakusch, J.; Verevkin, S.; Rüchardt, C. Abhangigkeit des inversen anomeren Effektes geminaler Nitril-Gruppen von der Struktur. Chem. Ber. 1990, 123, 2153–2159. [Google Scholar] [CrossRef]
- Verevkin, S.P. Improved Benson Increments for the Estimation of Standard Enthalpies of Formation and Enthalpies of Vaporization of Alkyl Ethers, Acetals, Ketals, and Ortho Esters. J. Chem. Eng. Data 2002, 47, 1071–1097. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Safronov, S.P.; Samarov, A.A.; Vostrikov, S.V. Hydrogen Storage: Thermodynamic Analysis of Alkyl-Quinolines and Alkyl-Pyridines as Potential Liquid Organic Hydrogen Carriers (LOHC). Appl. Sci. 2021, 11, 11758. [Google Scholar] [CrossRef]
- Rablen, P. A Procedure for Computing Hydrocarbon Strain Energies Using Computational Group Equivalents, with Application to 66 Molecules. Chemistry 2020, 2, 22. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).