Abstract
The antimicrobial activity of plants, algae, and derived extracts has been a subject of interest for the scientific community. Algae extracts have demonstrated their potential as a source of natural antimicrobial agents. Because of their antibacterial capacity and low toxicity, algae extracts have been studied as natural preservatives in food and cosmetic formulations. The use of these extracts has the potential to minimize the use of synthetic preservatives, which may be harmful to both human health and the environment. Nonetheless, the use of end-point techniques to calculate the minimal inhibitory concentration instead of creating growth inhibition curves usually leads to an absence of mathematical modeling procedures on the bacterial inhibition behavior of natural extracts. The goal of mathematical modeling is to describe the relationship between the concentration of an inhibitory agent (such as a drug or a toxin) and the growth rate of a population. For this purpose, the data obtained during the growth of six different bacteria in the presence of different concentrations of Ascophyllum nodosum (L.) extracts were recorded over 24 h. Later, the collected data were modeled based on different classical sigmoidal models, e.g., Weibull, logistic, and Gompertz, that were applied to define the critical growth phases and infer the kinetic parameters. The obtained parameters led to the conclusion that the inhibition mechanisms behind the antibacterial effects of the algae extracts are diverse towards different microorganisms. The presence of the extract led to a diminution of the specific growth velocity in some cases such as Staphylococcus epidermidis while in the replication of other bacteria such as Bacillus cereus, the extension of the lag phase was the predominant inhibition mechanism.
1. Introduction
Antimicrobial activity is an essential aspect of microbiology and public health. The ability of antibiotics, disinfectants, and other antimicrobial agents to inhibit the growth of bacteria and other microorganisms is critical for controlling infections and preventing, for instance, food spoilage. There is a panoply of natural products with antimicrobial properties [1,2], and the scientific community has been focused on those products especially for safety reasons. Macroalgae have shown great potential in several bioactive characteristics, including antimicrobial activity [3]. The antimicrobial capacity of Ascophyllum nodosum extracts was formerly reported [4].
Mathematical models can be used to describe the relationship between the concentration of an antimicrobial agent and the extent of growth inhibition. Three commonly used sigmoidal models for this purpose are the Weibull, Gompertz, and logistic models.
The Weibull model is a flexible model that can be used to describe a wide range of survival and growth processes [5]. The Weibull model assumes that the microbial population has a heterogeneous response to the antimicrobial agent, with a subset of cells being more resistant than others (Equation (1)).
where K represents the asymptote corresponding to the maximum growth, a is the curve slope and is related to the microbial growth velocity, and finally t50 represents the time to achieve 50% of the asymptotic value and is related to the lag time.
The Gompertz model is a sigmoidal model that is often used to describe bacterial growth curves. This model can be adapted to describe the effects of antimicrobial agents by incorporating an inhibitory effect (Equation (2)). Many modifications of this model have been proposed over the years [6].
where Ym is the asymptote is the maximum bacterial population, Y0 is the initial bacterial population, and 1/K provides the coordinates of the inflexion point.
The logistic function model characterizes the proliferation of microbial populations based on their starting population density, duration of growth, rate of growth, and ultimate population density [7]. This sigmoidal model is widely used, with or without modifications [8], to describe the growth of bacterial populations (Equation (3)).
where Ym and Y0 are the maximum bacterial population and starting bacterial population, correspondingly, and k is the rate constant.
In the present study, the three above-described sigmoidal models were fitted to the growth curves of six microorganisms in the presence of different concentrations of Ascophyllum nodosum extracts.
2. Materials and Methods
The antimicrobial activity growth curves in the presence of algae extracts used to fit the mathematical models were published by Silva and colleagues [4]. The following microorganisms were used: Gram-negative strains of Pseudomonas aeruginosa (ATCC 10145), Salmonella enteritidis (ATCC 13676), and Escherichia coli (NCTC 9001) as well as the Gram-positive strains of Staphylococcus aureus (ATCC 25923), Staphylococcus epidermidis (NCTC 11047), and Bacillus cereus (ATCC 14579).
The mathematical models and figures presented were created using GraphPad prism 8 software. The parameters were found after checking the normality of the residues by the Shapiro–Wilk test. Fisher’s F-test (α = 0.05) was used to figure out if the constructed models were appropriate to describe the observed data. Finally, the correlation coefficient R2 is interpreted as the proportion of variability in the dependent variable explained by the model.
3. Results and Discussion
The data were successfully fit to the three models, and the lowest correction factor R2 achieved was 0.9423 when fitting the Gompertz model to the growth curve of P. aeruginosa in the presence of 8 mg/mL of A. nodosum extract. The compilation of the adjusted factors is presented in Table 1.

Table 1.
Parameters estimated from the logistic, Weibull, and Gompertz equations (p < 0.05) and the correspondent coefficient of determination R2.
The results of the global analysis showed that all three classical sigmoid models can adequately stand for the experimental data. However, the Weibull model achieved the best overall R2 value, showing that it is the most effective model for fitting the experimental data. Previous studies have also shown that the Weibull model outperforms the commonly used Gompertz model for fitting empirical data [9,10]. Figure 1 presents the growth curves of the microorganisms and the corresponding parameters determined by the Weibull model.
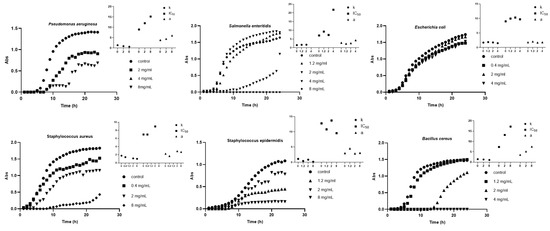
Figure 1.
Growth curves of the microorganism and the corresponding parameters of the Weibull equation • represents K, ▪ represents t50, and ▲ represents the a. Adapted from Ref. [4].
Considering the results in Table 1, in the case of P. aeruginosa behavior in the presence of the algae extract, it is possible to infer that the antimicrobial agent led to a decrease in the maximum bacterial population k, ranking from 1.370 to 0.6608, but also affected the lag time, which is the period of time during which bacteria or other microorganisms adapt to their new environment and begin to grow and reproduce and is reflected in the factor t50. The primary mechanism in the case of S. enteritidis and B. cereus appears to be the extension of lag time, with the t50 parameter varying from 7.049 to 21.80 in the first case and from 7.323 to 17.21 in the second, while the k and a factors had minor variations. In the case of S. epidermidis, the maximum bacterial density was the most important factor affected by antimicrobial action, the k parameter varied from 1.093 to 0.1583, while in the case of E. coli, the invariability of the parameters determined it was consistent with the lack of inhibition observed.
This work showed that the Weibull model can be used with advantage to describe antimicrobial action of natural extracts.
Author Contributions
Conceptualization, M.A.P. and A.S.; methodology, P.B.; software F.C. and J.E.; validation, M.F.B.; formal analysis, C.L.-L.; investigation, A.S. and P.G.-O.; resources, M.A.P.; data curation, M.A.P.; writing—original draft preparation, A.S.; writing—review and editing, M.C.; visualization, P.G.-O. and F.C.; supervision, J.S.-G.; project administration, M.F.B. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results was supported by MICINN supporting the Ramón y Cajal grant for M.A. Prieto (RYC-2017-22891) and the pre-doctoral grants of P. Garcia-Oliveira (ED481A-2019/295) and M. Carpena (ED481A 2021/313). The authors thank the program BENEFICIOS DO CONSUMO DAS ESPECIES TINTORERA-(CO-0019-2021) that supports the work of F. Chamorro. The authors are grateful to the Ibero-American Program on Science and Technology (CYTED—AQUA-CIBUS, P317RT0003), to the Bio Based Industries Joint Undertaking (JU) under grant agreement No 888003 UP4HEALTH Project (H2020-BBI-JTI-2019) of C. Lourenço-Lopes, and to AlgaMar company (www.algamar.com) for the collaboration and algae material provision. The authors would like to thank the EU and FCT for funding through the programs UIDB/50006/2020; UIDP/50006/2020 and the authors are grateful to the Ibero-American Program on Science and Technology (CYTED—GENOPSYSEN, P222RT0117). MFB thanks FCT for the FCT Investigator (2020.03107.CEECIND).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available at Ref. [4].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gonelimali, F.D.; Lin, J.; Miao, W.; Xuan, J.; Charles, F.; Chen, M.; Hatab, S.R. Antimicrobial Properties and Mechanism of Action of Some Plant Extracts Against Food Pathogens and Spoilage Microorganisms. Front. Microbiol. 2018, 9, 1639. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Silva, S.A.; Lourenço-Lopes, C.; Jimenez-Lopez, C.; Carpena, M.; Gullón, P.; Fraga-Corral, M.; Domingues, V.F.; Barroso, M.F.; Simal-Gandara, J.; et al. Antibacterial Use of Macroalgae Compounds against Foodborne Pathogens. Antibiotics 2020, 9, 712. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Cassani, L.; Grosso, C.; Garcia-Oliveira, P.; Morais, S.L.; Echave, J.; Carpena, M.; Xiao, J.; Barroso, M.F.; Simal-Gandara, J.; et al. Recent advances in biological properties of brown algae-derived compounds for nutraceutical applications. Crit. Rev. Food Sci. Nutr. 2022, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Cassani, L.; Lourenço-Lopes, C.; Morais, S.L.; Cao, H.; Garcia-Oliveira, P.; Garcia-Perez, P.; Carpena, M.; Domingues, V.; Barroso, M.F.; et al. Antimicrobial Activity of Crude Extracts from Ascophyllum nodosum Obtained by Microwave-Assisted Extraction. Med. Sci. Forum 2022, 12, 19. [Google Scholar] [CrossRef]
- Buzrul, S. The Weibull Model for Microbial Inactivation. Food Eng. Rev. 2022, 14, 45–61. [Google Scholar] [CrossRef]
- Tjørve, K.M.C.; Tjørve, E. The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family. PLoS ONE 2017, 12, e0178691. [Google Scholar] [CrossRef] [PubMed]
- Wachenheim, D.E.; Patterson, J.A.; Ladisch, M.R. Analysis of the logistic function model: Derivation and applications specific to batch cultured microorganisms. Bioresour. Technol. 2003, 86, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Fujikawa, H.; Kai, A.; Morozumi, S. A New Logistic Model for Bacterial Growth. J. Food Hyg. Soc. Japan 2003, 44, 155–160. [Google Scholar] [CrossRef] [PubMed]
- López, S.; Prieto, M.; Dijkstra, J.; Dhanoa, M.S.; France, J. Statistical evaluation of mathematical models for microbial growth. Int. J. Food Microbiol. 2004, 96, 289–300. [Google Scholar] [CrossRef] [PubMed]
- Dagogo, J.; Cynthia, O.U.; Oyinebifun Biu, E. Comparative Analysis of Additive and Multiplicative Error Terms of Weibull, Logistic Gompertz, Hills and Richards Models with Four Parameters. J. Adv. Math. Comput. Sci. 2023, 38, 1–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).